当前位置： 首页 > news >正文

香橙派pi5下，debian，docker19.03.9版本runc容器逃逸

news 2026/2/10 1:06:13

在香橙派pi5下，debian，docker19.03.9版本下，安装系统后，启动docker，显示一切正常。

当加入k8s集群以后，可以正常连接到集群，node状态显示为ready。看起来一切正常。不过过一会之后，香橙派节点内存飙升，然后挂掉。重连失败，需要重启后才能重连。且swapoff -a命令执行后才出问题，不执行，内存不爆掉，但node状态也一直是not ready

经top命令查看，有一个runc命令在一直运行，产生了诸多实例，且随着时间的推移，runc命令产生的越来越多。

然后进入香橙派docker下执行docker images 命令只发现了pause一个镜像，没有发现正常需要的flannel镜像和容器。

按理说，加入k8s集群以后,node节点会自动拉取flannel镜像，并启动为容器。现在看，并没有找到对应的镜像和容器。

当时就产生了一个疑问：虽然没有看到容器，但是实际上确实已经连接到集群了。当时就产生了怀疑，怎么会这样呢，难道docker也有类似k8s命名空间的概念？按理说没有啊。

然后使用docker ps查看，也是没有容器。但是当使用docker ps -a的时候，发现一大堆一大堆的pause和flannel的容器，并且随时时间的推移在不停的增长。

 

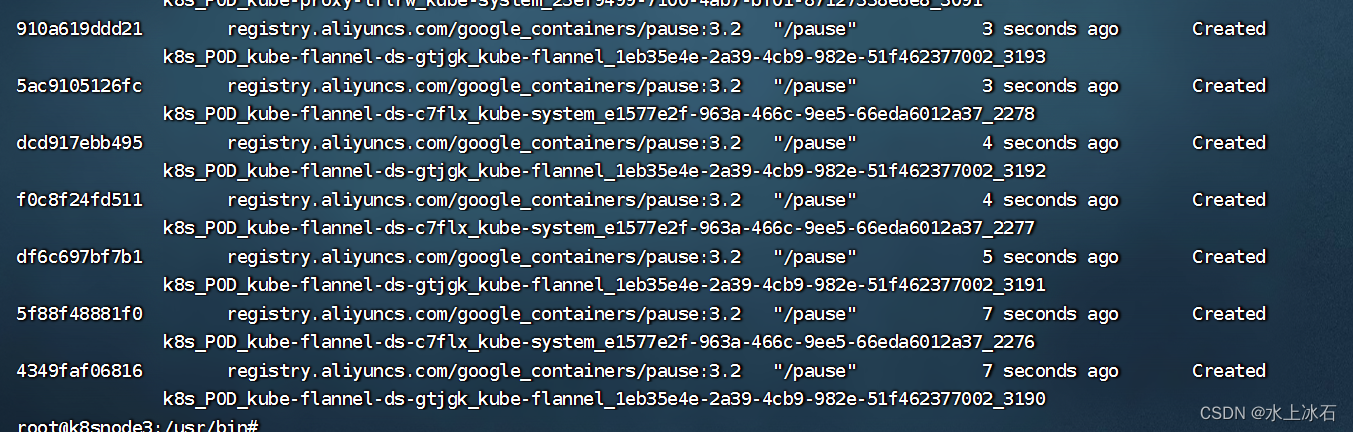
相关文章：

香橙派pi5下，debian，docker19.03.9版本runc容器逃逸

在香橙派pi5下，debian，docker19.03.9版本下，安装系统后，启动docker，显示一切正常。 当加入k8s集群以后，可以正常连接到集群，node状态显示为ready。看起来一切正常。不过过一会之后，香橙派节点内存飙升，然后挂掉。重连失败，需要重启后才能重连。且swapoff -a命令执行…...

编程日记 2023/4/16 20:38:44

Thinkphp6.0中间件.上

本节课我们来学习一下中间件的用法，定义一下中间件。 一．定义中间件 1. 中间件的主要用于拦截和过滤 HTTP 请求，并进行相应处理； 2. 这些请求的功能可以是 URL 重定向、权限验证等等； 3. 为了进一步了解中间件的用法&…...

编程日记 2023/5/29 21:52:36

十进制到八进制的转换

目录 十进制到八进制的转换 程序设计 程序分析 十进制到八进制的转换 【问题描述】对于输入的任意一个非负十进制整数n(0=<n<100000)，打印输出与其等值的八进制数 【输入形式】非负十进制整数 【输出形式】相应十进制整数转换后的八进制正整数，若输入不符合要求，…...

编程日记 2023/5/31 21:13:25

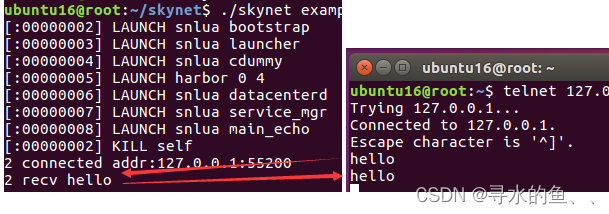
【从零开始学Skynet】基础篇（四）：网络模块常用API

游戏服务端要处理客户端请求&#xff0c;作为服务端引擎&#xff0c;网络编程也是Skynet的核心功能。1、学习网络模块 skynet.socket模块提供了网络编程的API&#xff0c;常用的API如下表所示&#xff1a;Lua API说明socket.listen(address ,port)监听一个端口&#xff0c;返回…...

编程日记 2023/4/16 20:23:40

怎么免费制作logo？logo免费设计在线生成，从此设计不求人

你有没有因为Logo制作而烦恼过&#xff1f;对于很多人来说&#xff0c;logo制作是一项比较大的工程&#xff0c;需要专门的设计师才能完成。但是请人设计费用高还很费时间&#xff0c;还需多次沟通修改。其实&#xff0c;我们可以自己免费制作logo&#xff0c;下面&#xff0c;…...

编程日记 2023/4/16 20:18:39

【目标检测】目标检测遇上知识图谱：Object detection meets knowledge graphs论文解读与复现

前言 常规的目标检测往往是根据图像的特征来捕捉出目标信息&#xff0c;那么是否有办法加入一些先验信息来提升目标检测的精准度&#xff1f; 一种可行的思路是在目标检测的输出加入目标之间的关联信息&#xff0c;从而对目标进行干涉。 2017年8月&#xff0c;新加波管理大学…...

编程日记 2023/4/16 20:13:38

IDEA重复下载SNAPSHOT包问题

问题现象 reimport 之后 状态栏显示resolving dependencies… 遇到某个比较大的快照包(33M)&#xff0c;同一天的第2个版本时 1.0-xxx-SNAPSHOT.时间戳-2 idea importer 会先分片下载 x.jar.part文件中&#xff0c;然后复制为x.jar吧 如图中所示&#xff0c;其实已经下载完了&…...

编程日记 2023/4/16 20:08:36

【Unity入门】12.MonoBehaviour事件函数

【Unity入门】MonoBehaviour事件函数 大家好&#xff0c;我是Lampard~~ 欢迎来到Unity入门系列博客&#xff0c;所学知识来自B站阿发老师~感谢 &#xff08;一&#xff09;常用的事件函数 &#xff08;1&#xff09;start和update方法 之前我们写的脚本&#xff0c;会默认帮助…...

编程日记 2023/4/16 20:03:34

1.3 Docker Compose-详细介绍

Docker Compose是一个用于定义和运行多个Docker容器的工具。它可以让用户轻松地定义和管理多个容器的配置&#xff0c;并且可以通过简单的命令来启动、停止和重启这些容器。在本文中&#xff0c;我们将详细介绍Docker Compose的使用和功能。 一、Docker Compose的安装 Docker…...

编程日记 2023/4/16 19:58:32

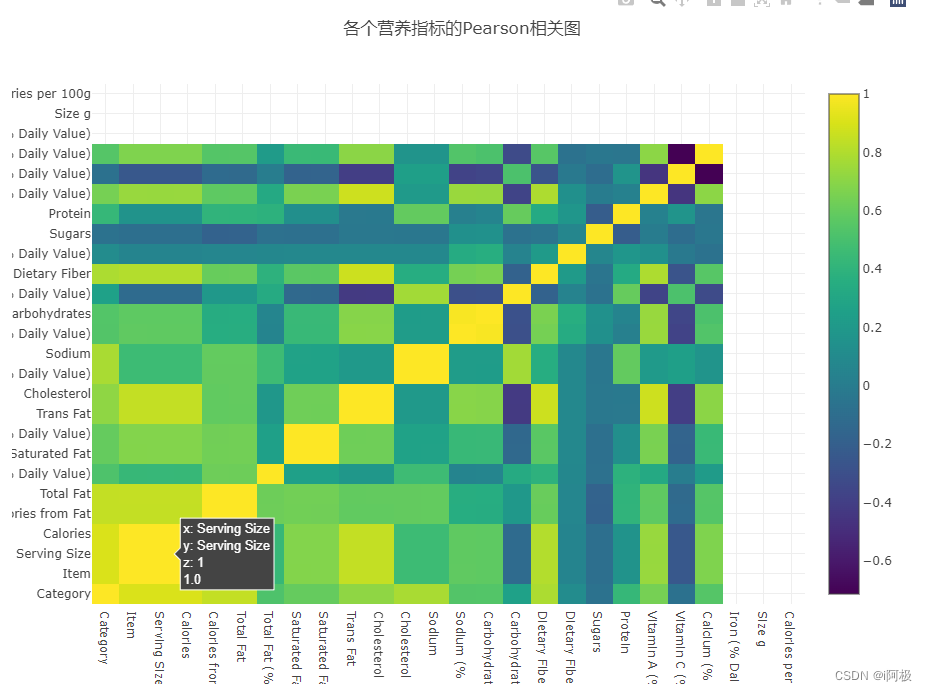
数据分析：麦当劳食品营养数据探索并可视化

系列文章目录 作者&#xff1a;i阿极 作者简介&#xff1a;Python领域新星作者、多项比赛获奖者&#xff1a;博主个人首页 &#x1f60a;&#x1f60a;&#x1f60a;如果觉得文章不错或能帮助到你学习&#xff0c;可以点赞&#x1f44d;收藏&#x1f4c1;评论&#x1f4d2;关注…...

编程日记 2023/4/16 19:53:30

ES6标准

ECMAScript 6.0&#xff08;以下简称 ES6&#xff09;是 JavaScript 语言的下一代标准 前端es6是模块化开发&#xff1b;es6模块化规范就是浏览器端与服务器端通用的模块化开发规范&#xff0c;其中定义了每一个JavaScript文件都是一个独立的模块&#xff0c;导入其他模块成员…...

编程日记 2023/4/16 19:48:29

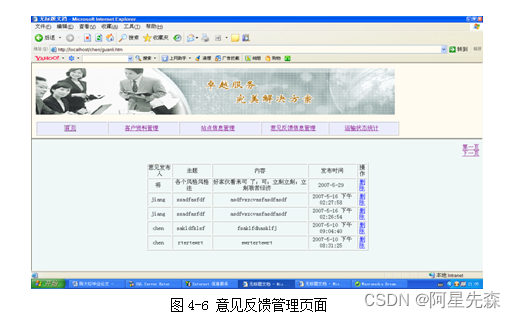
ASP一个物流商品运输系统的设计与实现

物流运输行业的今天正朝着追求高效、低成本、稳定可靠的方向发展。本文详细介绍了网上物流管理系统&#xff0c;涉及到客户端运输线路设计、过程跟踪等功能模块以及管理员端的相应模块的具体实现&#xff0c;分析了整个系统的架构、工作原理、实现功能等。系统采用ASPMS SQL以B…...

编程日记 2023/4/16 19:43:27

肖 sir_就业课__009ui自动化讲解

ui自动化讲解 1、你做过自动化测试吗&#xff1f;做过 ui自动化测试、接口自动化、app自动化 2、你讲下你做的ui接口自动化&#xff1f; &#xff08;1&#xff09;第一种&#xff1a;按照线性流程讲解 &#xff1a;pythonselenium 库做ui自动化 &#xff08;2&#xff09;第二…...

编程日记 2023/4/16 19:38:26

「线性DP」花店橱窗

花店橱窗 https://ac.nowcoder.com/acm/contest/24213/1005 题目描述 ​ 小q和他的老婆小z最近开了一家花店&#xff0c;他们准备把店里最好看的花都摆在橱窗里。 ​ 但是他们有很多花瓶&#xff0c;每个花瓶都具有各自的特点&#xff0c;因此&#xff0c;当各个花瓶中放入不同…...

编程日记 2023/4/16 19:33:25

数组的去重方法

1、ES6的Set方法去重 new Set是ES6新推出的一种类型。它和数组的区别在于&#xff0c;Set类型中的数据不可以有重复的值。当然&#xff0c;数组的一些方法Set也无法调用。 使用方法&#xff1a;将一个数组转化为Set数据&#xff0c;再转化回来&#xff0c;就完成了去重。 cons…...

编程日记 2023/6/1 5:47:35

ESP32-LORA通信

文章目录好久没更新博客了&#xff0c;今天清明节&#xff0c;写个LORA通信。在此记念在天堂的外婆。祝她安好LORA通信简介一、模块二、使用步骤1.电脑通过USB串口模块联接LORA模块2.ESP32连接LORA通信进行收发通信3.电脑运行调试助手&#xff0c;ESP32运行代码。实现LORA通信测…...

编程日记 2023/5/31 3:32:22

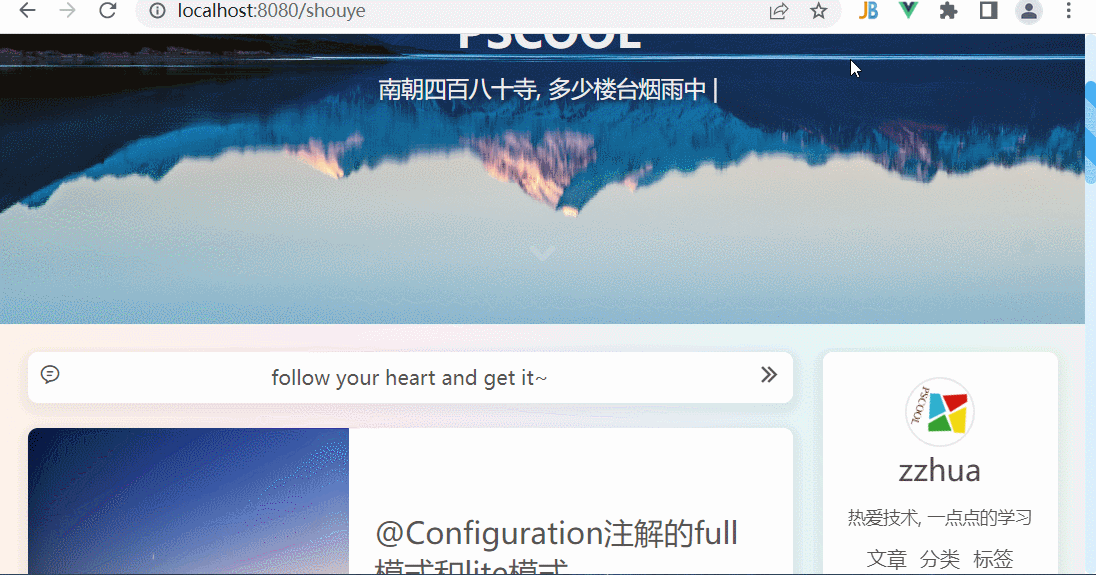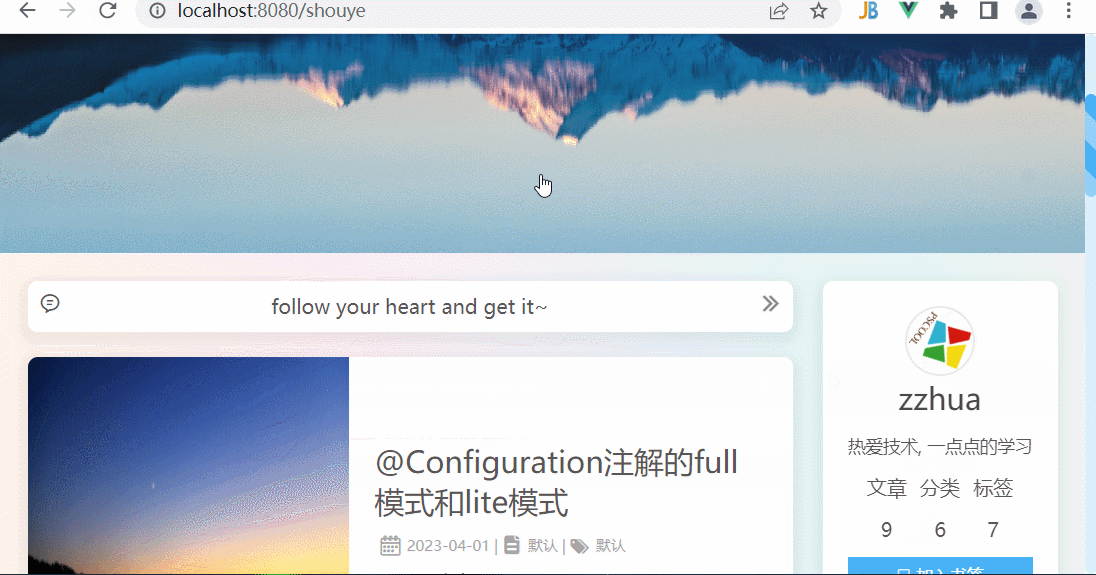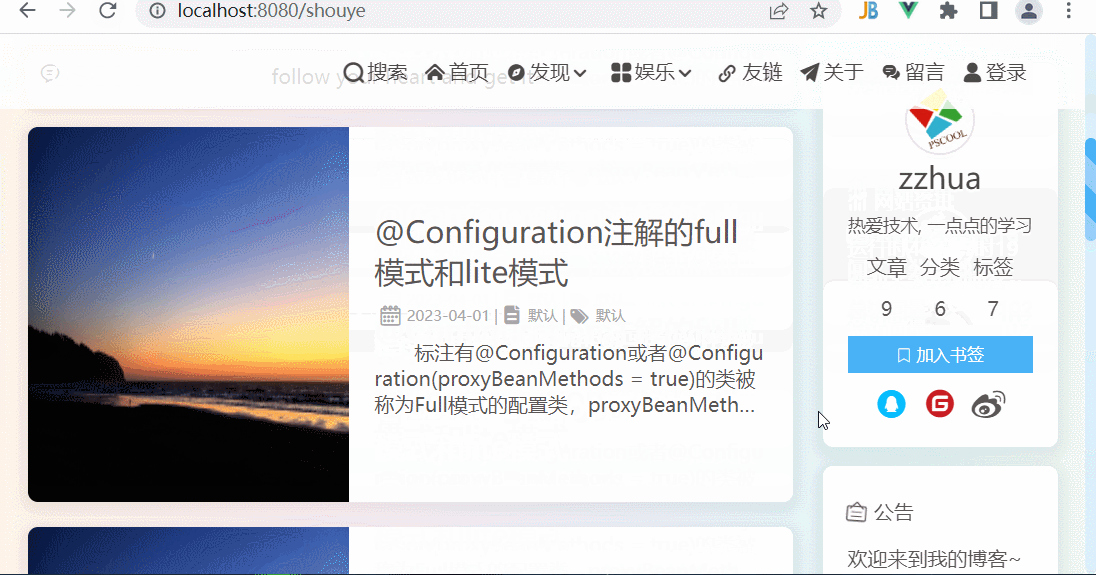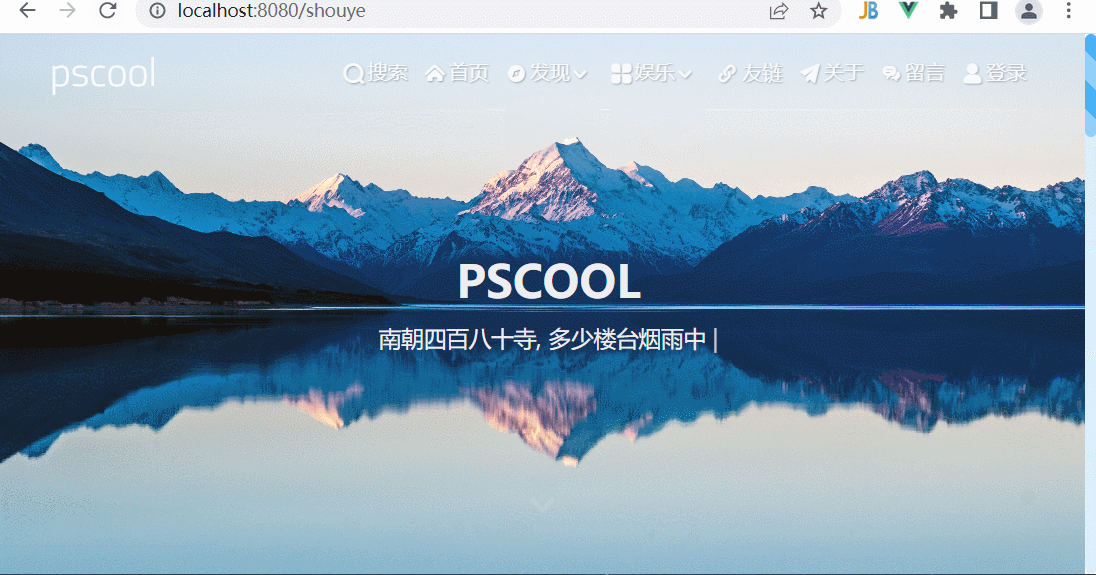
博客首页效果

学习来自风宇blog的博客首页效果 全部用的基本上都是原生的html&#xff0c;css&#xff0c;js特别是flex布局的使用&#xff0c;主轴方向可以是横轴&#xff0c;也可以是纵轴&#xff0c;弹性项还可可以使用百分比sticky粘性布局&#xff0c;作为侧边栏&#xff0c;它不会超出…...

编程日记 2023/4/16 19:18:19

【LeetCode】剑指 Offer（29）

目录 题目&#xff1a;剑指 Offer 56 - II. 数组中数字出现的次数 II - 力扣&#xff08;Leetcode&#xff09; 题目的接口&#xff1a; 解题思路&#xff1a; 代码&#xff1a; 过啦&#xff01;&#xff01;&#xff01; 题目&#xff1a;剑指 Offer 57. 和为s的两个数…...

编程日记 2023/4/16 19:13:18

自然语言处理（八）：Lexical Semantics

目录 1. Sentiment Analysis 2. Lexical Database 2.1 What is Lexical Database 2.2 Definitions 2.3 Meaning Through Dictionary 2.4 WordNet 2.5 Synsets 2.6 Hypernymy Chain 3. Word Similarity 3.1 Word Similarity with Paths 3.2 超越路径长度 3.3 Abstra…...

编程日记 2023/5/31 3:33:49

推荐一款 AI 脑图软件，助你神速提高知识体系搭建

觅得一款神器&#xff0c;接近我理想中&#xff0c;搭建知识体系的方法&#xff0c;先来看视频作为数据库开发或管理者&#xff0c;知识体系搭建尤为重要。来看看近些年缺乏足够数据库知识面造成的危害&#xff1a;a/ 数据安全风险&#xff1a;例如&#xff0c;2017年Equifax数…...

编程日记 2023/4/16 19:03:16

论文解读：交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架（二）

HoST框架核心实现方法详解 - 论文深度解读（第二部分） 《Learning Humanoid Standing-up Control across Diverse Postures》 系列文章： 论文深度解读 + 算法与代码分析（二） 作者机构： 上海AI Lab, 上海交通大学, 香港大学, 浙江大学, 香港中文大学 论文主题： 人形机器人…...

编程新知 2026/2/9 0:12:12

golang循环变量捕获问题​​

在 Go 语言中&#xff0c;当在循环中启动协程&#xff08;goroutine&#xff09;时&#xff0c;如果在协程闭包中直接引用循环变量&#xff0c;可能会遇到一个常见的陷阱 - ​​循环变量捕获问题​​。让我详细解释一下&#xff1a; 问题背景 看这个代码片段&#xff1a; fo…...

编程新知 2026/1/21 14:29:57

【力扣数据库知识手册笔记】索引

索引 索引的优缺点 优点1. 通过创建唯一性索引&#xff0c;可以保证数据库表中每一行数据的唯一性。2. 可以加快数据的检索速度&#xff08;创建索引的主要原因&#xff09;。3. 可以加速表和表之间的连接&#xff0c;实现数据的参考完整性。4. 可以在查询过程中&#xff0c;…...

编程新知 2026/1/25 4:36:37

Swift 协议扩展精进之路：解决 CoreData 托管实体子类的类型不匹配问题（下）

概述 在 Swift 开发语言中&#xff0c;各位秃头小码农们可以充分利用语法本身所带来的便利去劈荆斩棘。我们还可以恣意利用泛型、协议关联类型和协议扩展来进一步简化和优化我们复杂的代码需求。 不过&#xff0c;在涉及到多个子类派生于基类进行多态模拟的场景下&#xff0c;…...

编程新知 2026/1/23 4:56:05

SCAU期末笔记 - 数据分析与数据挖掘题库解析

这门怎么题库答案不全啊日 来简单学一下子来 一、选择题&#xff08;可多选&#xff09; 将原始数据进行集成、变换、维度规约、数值规约是在以下哪个步骤的任务?(C) A. 频繁模式挖掘 B.分类和预测 C.数据预处理 D.数据流挖掘 A. 频繁模式挖掘&#xff1a;专注于发现数据中…...

编程新知 2026/1/24 14:15:43

ElasticSearch搜索引擎之倒排索引及其底层算法

文章目录 一、搜索引擎1、什么是搜索引擎？2、搜索引擎的分类3、常用的搜索引擎4、搜索引擎的特点二、倒排索引1、简介2、为什么倒排索引不用B+树1.创建时间长，文件大。2.其次，树深，IO次数可怕。3.索引可能会失效。4.精准度差。三. 倒排索引四、算法1、Term Index的算法2、 …...

编程新知 2026/1/30 17:10:19

Axios请求超时重发机制

Axios 超时重新请求实现方案 在 Axios 中实现超时重新请求可以通过以下几种方式&#xff1a; 1. 使用拦截器实现自动重试 import axios from axios;// 创建axios实例 const instance axios.create();// 设置超时时间 instance.defaults.timeout 5000;// 最大重试次数 cons…...

编程新知 2025/10/13 2:26:14

mysql已经安装，但是通过rpm -q 没有找mysql相关的已安装包

文章目录 现象&#xff1a;mysql已经安装&#xff0c;但是通过rpm -q 没有找mysql相关的已安装包遇到 rpm 命令找不到已经安装的 MySQL 包时&#xff0c;可能是因为以下几个原因&#xff1a;1.MySQL 不是通过 RPM 包安装的2.RPM 数据库损坏3.使用了不同的包名或路径4.使用其他包…...

编程新知 2026/2/4 16:17:25

高效线程安全的单例模式：Python 中的懒加载与自定义初始化参数

高效线程安全的单例模式：Python 中的懒加载与自定义初始化参数 在软件开发中，单例模式（Singleton Pattern）是一种常见的设计模式，确保一个类仅有一个实例，并提供一个全局访问点。在多线程环境下，实现单例模式时需要注意线程安全问题，以防止多个线程同时创建实例，导致…...

编程新知 2025/11/25 19:50:27

Redis：现代应用开发的高效内存数据存储利器

一、Redis的起源与发展 Redis最初由意大利程序员Salvatore Sanfilippo在2009年开发&#xff0c;其初衷是为了满足他自己的一个项目需求&#xff0c;即需要一个高性能的键值存储系统来解决传统数据库在高并发场景下的性能瓶颈。随着项目的开源&#xff0c;Redis凭借其简单易用、…...

编程新知 2025/11/15 1:41:43