数据结构-排序
本节目标:
1.排序的概念及其运用
2.常见排序算法的实现
3.排序算法复杂度及稳定性分析
1.排序的概念及其应用
1.1排序的概念
排序就是按照某个我们设定的关键字,或者关键词,递增或者递减,完成这样的操作就是排序。
1.2排序的应用
排序在日常生活中很常见的,想前几天刚出的软科高校排名,就用到了排序的思想,关键词就是软科,按照递增的顺序排列。如下图所示:
以及我们上淘宝的时候,也会用到排序的思想,我们想买个手机,筛选条件,按照个人选择不同给出的答案不同,用的人注重品牌,有的人注重价格,有的女孩更注重像素,如下图所示:
1.3常见的排序算法
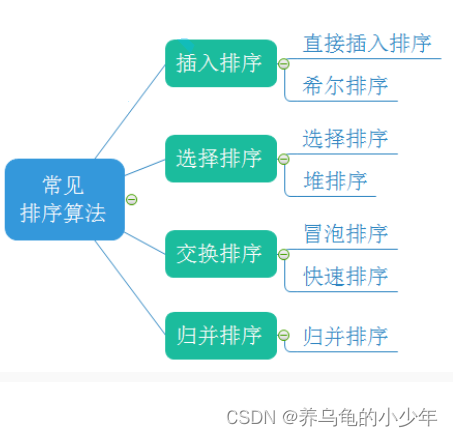
2.常见的排序算法实现
2.1插入排序
2.1.1基本思想
其实插入排序的思想,几乎我们每个人都会,插入排序就像我们打的扑克,从未知的一副牌中,我们开始往手里揭牌,拿起第一张放在手中,再次拿起一张牌的时候,就要和手里的牌对比,如果比手里的牌大就往后排,如果比手里的牌小的话,就排在这张牌之前,以此类推。一副牌拿完之后,我们手里的牌也就按照递增的顺序排好了。

2.1.2直接插入排序:
当插入第i(i>=1)个元素时,前面的array[0],array[1],…,array[i-1]已经排好序,此时用array[i]的排序码与array[i-1],array[i-2],…的排序码顺序进行比较,找到插入位置即将array[i]插入,原来位置上的元素顺序后移。图解如下:
当插入的数比前一个数字还大时:

当插入的数字比数组中所有的数都要小的时候:
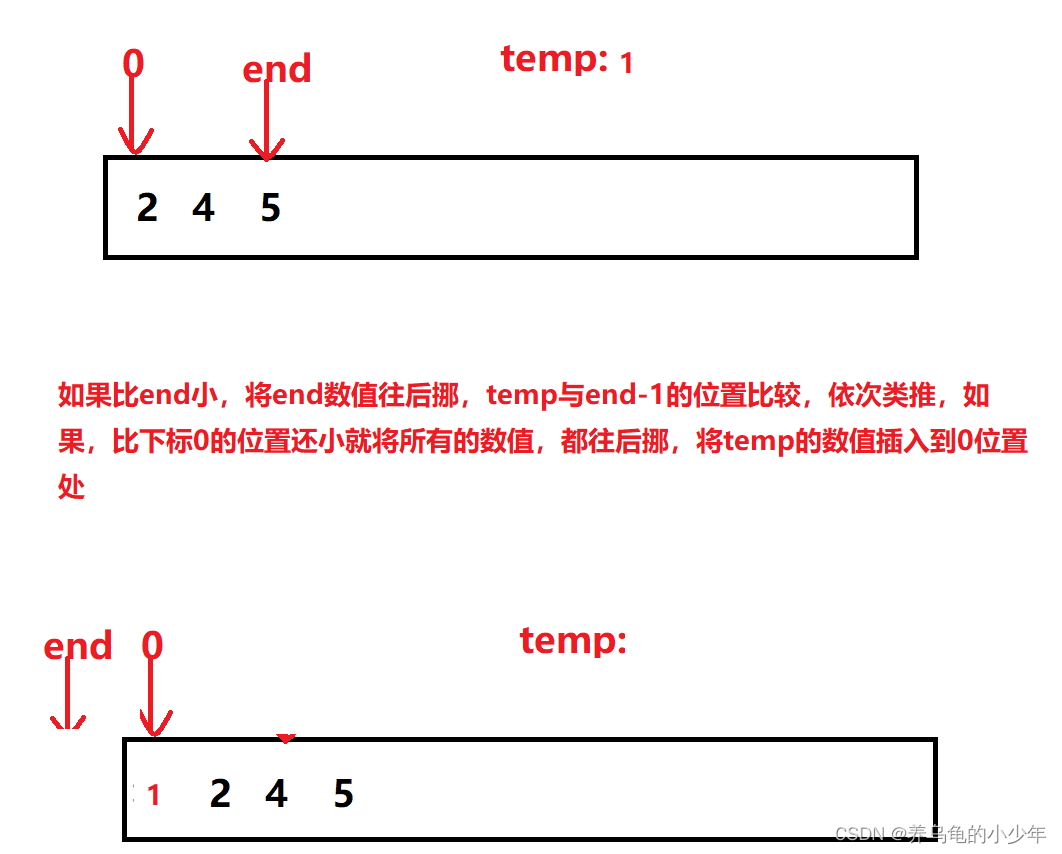
动态图解如下:
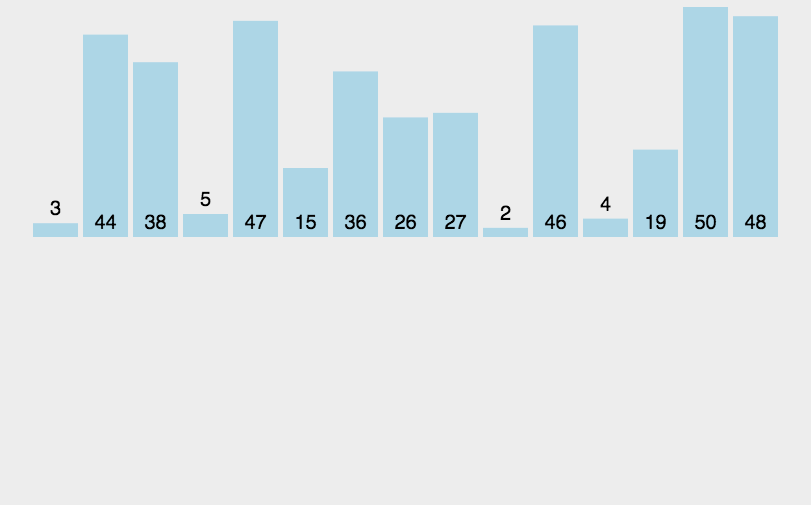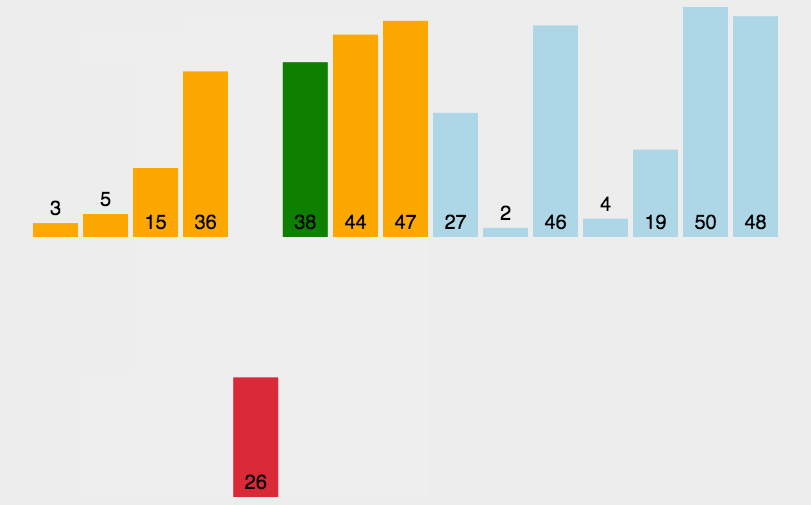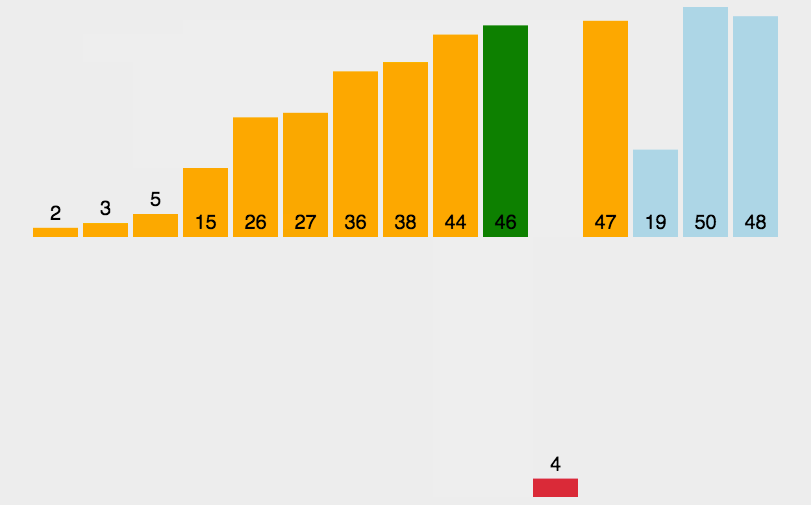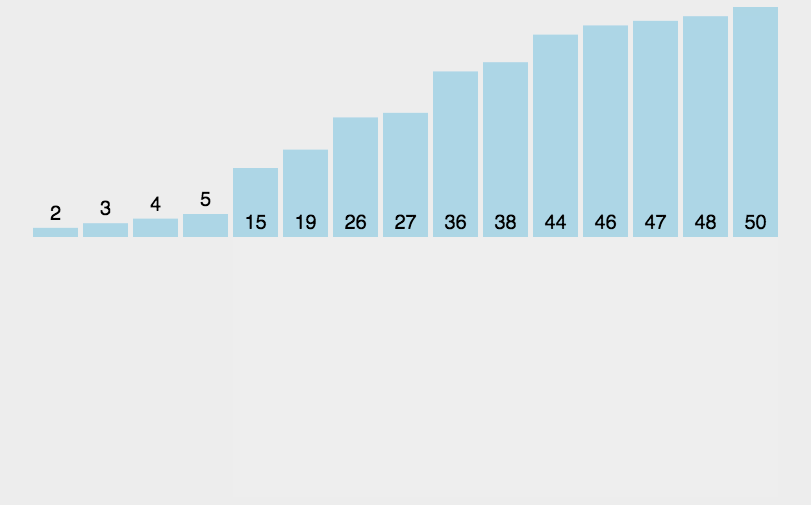
代码实现:
void InsertSort(int* a, int n)
{//遍历数组中所有元素for (int i = 1; i < n; i++){//单趟排序int end = i - 1;int temp = a[i];//temp存储的是元素数值while (end >= 0)//一直比较到 数组第一个元素完成{if (temp < a[end]){a[end + 1] = a[end];--end;}else // 包含两种情况,一种temp比所有元素都大,另一种temp比所有元素都小{break;}}a[end + 1] = temp;}
}结果对比:
在主程序中,我们调用插入排序函数,并查看最终是否实现 有序排序。
void TestInsertSort()
{int a[] = { 3,5,1,6,2,3,7,9,0,8 };PrintArray(a, sizeof(a) / sizeof(int));InsertSort(a, sizeof(a) / sizeof(int));PrintArray(a, sizeof(a) / sizeof(int));
}int main()
{TestInsertSort();return 0;
} 
分析总结:
直接插入排序时间复杂度:最坏情况下,逆序有序,每个元素都要一个个比较,最终形成等差数列, 1 +2 +3 + ........N 时间复杂度为 O(N^2) ;最好的情况下,有序,1 + 1 + 1 + .......1时间复杂度为O(N) 总结来看 对于插入排序,元素集合越接近有序,算法时间效率越高。
2.1.3希尔排序(缩小增量排序):
希尔排序也是插入排序的一种,它又称缩小增量排序法,他其实是在插入排序上的一种优化,通过上面的分析,我们知道插入排序时间复杂度最好的情况,也就是接近有序的时候,他的时间复杂度为 O(N),最坏的情况下 无序的时候 为 O(N^2)。如果我们能先让数组接近有序之后,在对他进行排序,会大大减小算法时间复杂度。所以希尔大佬就研究出了希尔排序。
它的实现主要通过两步骤,第一步:预排序,让数组接近有序,第二步:插入排序。
分组预排:
将无序的数组,按照间隙gap进行分组,将数组分成n/gap组,然后分组进行插入排序,因为有了gap所以时间复杂度会减小,如下图所示:
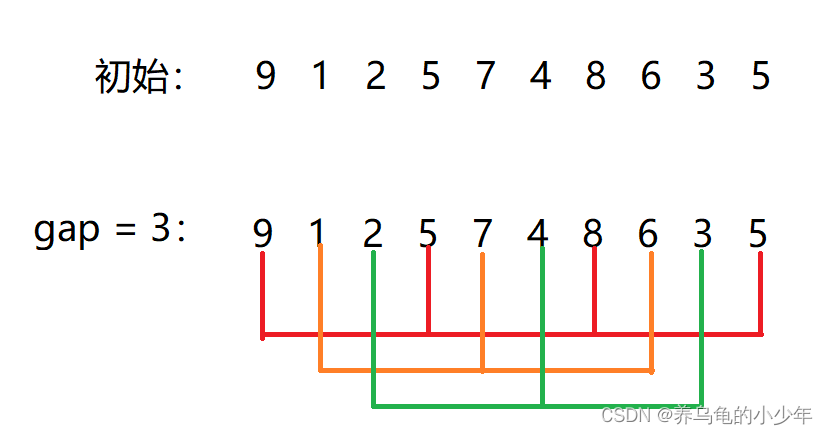
分组直接插入排序:
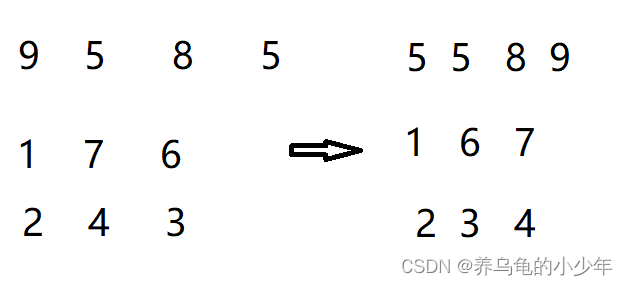
gap为3排序实现结果:
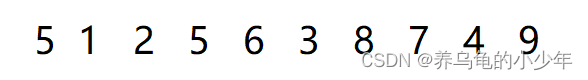
当gap依次减小,数组慢慢接近有序,最后gap为1时候,数组已经近似有序,再插入排序依次,数组就会实现有序的同时,算法时间复杂度最低。
代码实现:
void ShellSort(int* a, int n)
{int gap = 3;for (int j = 0; j < gap; j++){for (int i = j; i <n- gap; i += gap){//单趟排序int end = i;int temp =a[i + gap];//temp存储的是元素数值 i + gap 要在数组之内 不可以越界while (end >= 0)//一直比较到 数组第一个元素完成{if (temp < a[end]){a[end + gap] = a[end];end = end - gap;}else // 包含两种情况,一种temp比所有元素都大,另一种temp比所有元素都小{break;}}a[end + gap] = temp;}}}改进一下:
void ShellSort(int* a, int n)
{int gap = 3;for (int i = 0; i <n- gap; i ++){//单趟排序int end = i;int temp =a[i + gap];//temp存储的是元素数值 i + gap 要在数组之内 不可以越界while (end >= 0)//一直比较到 数组第一个元素完成{if (temp < a[end]){a[end + gap] = a[end];end = end - gap;}else // 包含两种情况,一种temp比所有元素都大,另一种temp比所有元素都小{break;}}a[end + gap] = temp;}
}我们发现gap越大虽然,跑的很快但是不接近有序,gap越小跑的慢,但是接近有序,所以需要设计合适的gap,减少复杂度的同时,保证最后一次排序 gap为1,通常 我们设计的gap,为n / 2,或者 n/3 - 1。
具体代码如下:
void ShellSort(int* a, int n)
{int gap = n ;while (gap > 1){gap /= 2;//gap = gap/3 - 1;for (int i = 0; i <n- gap; i ++){//单趟排序int end = i;int temp =a[i + gap];//temp存储的是元素数值 i + gap 要在数组之内 不可以越界while (end >= 0)//一直比较到 数组第一个元素完成{if (temp < a[end]){a[end + gap] = a[end];end = end - gap;}else // 包含两种情况,一种temp比所有元素都大,另一种temp比所有元素都小{break;}}a[end + gap] = temp;}}
}结果:
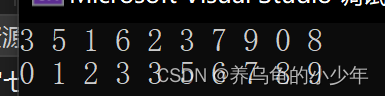
分析总结:
希尔排序的时间复杂度分析:
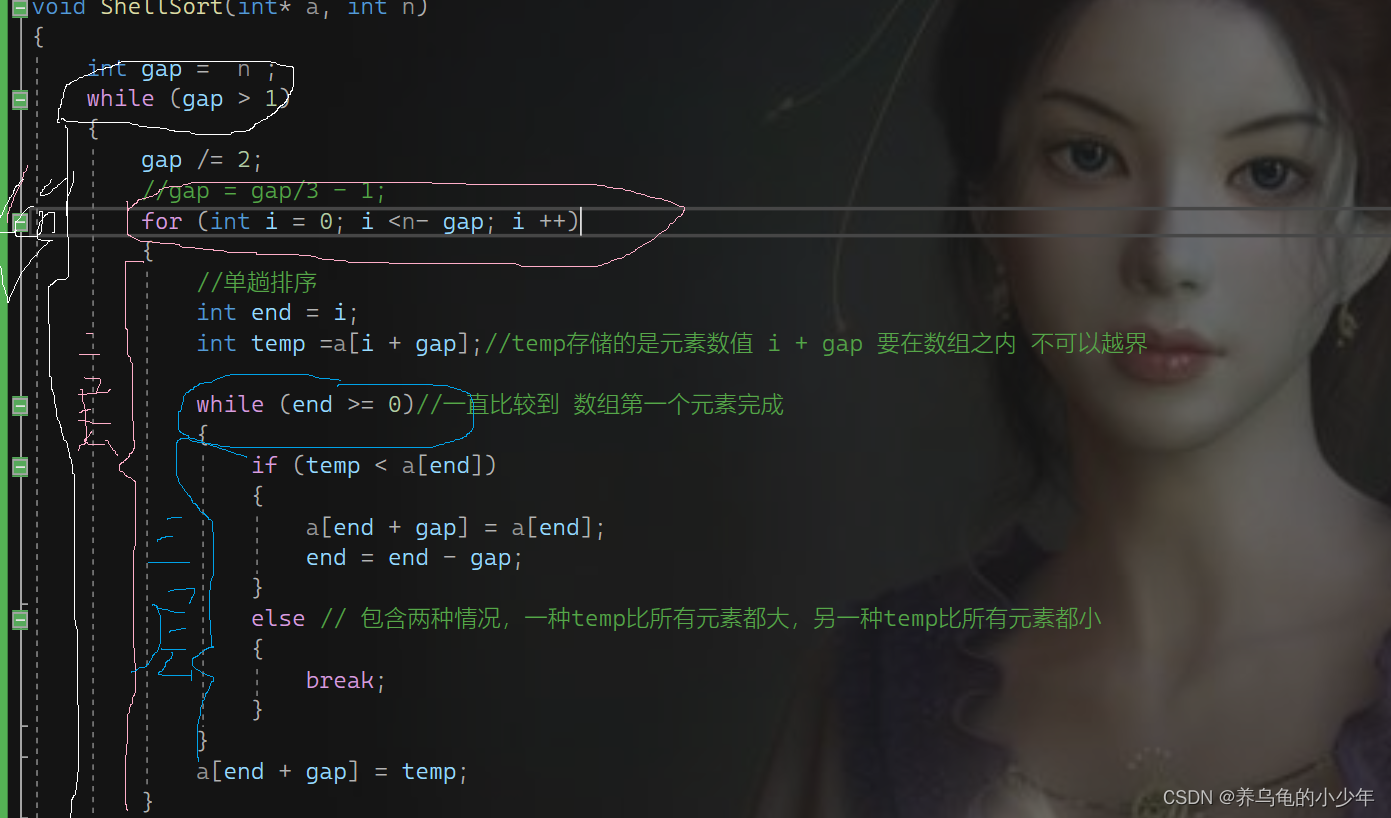
对于外层:是我们熟悉的二分或者三分 复杂度 最后为logN

对于内部两层,当gap很大时候,可以看成N,当gap很小时,经过多次预排序,接近有序 复杂度也是N,我们在以gap/3分析中间的变化:图解分析如下:
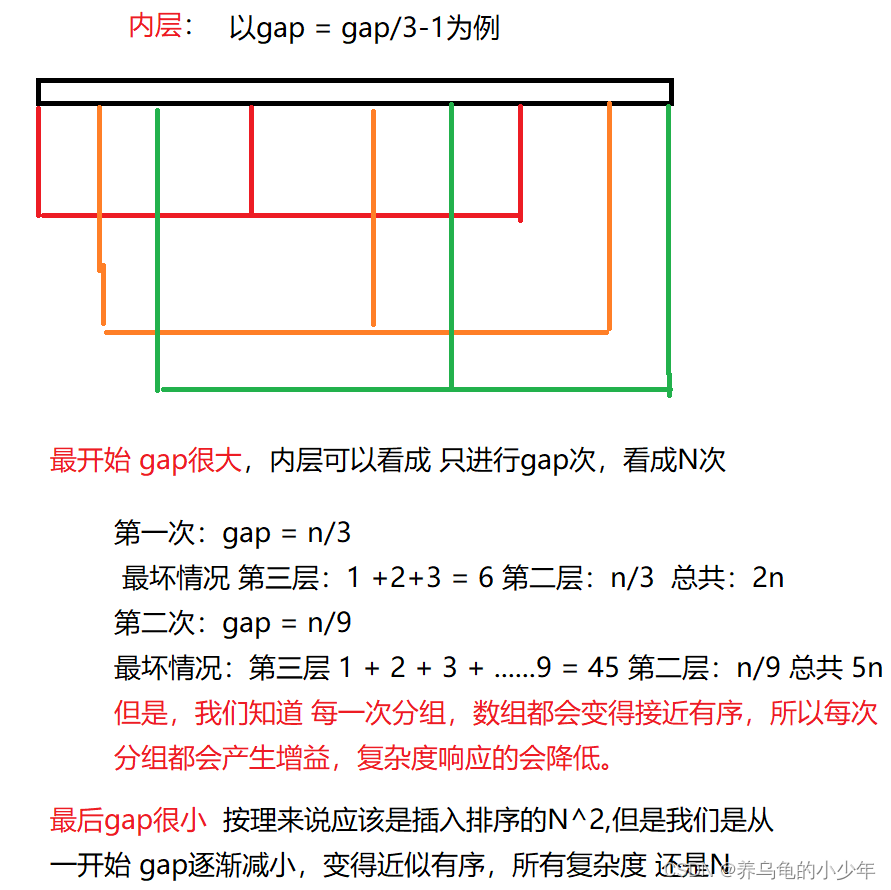
所以 我们可以说 希尔排序时间复杂度近似 N*logN 但是每次预排都会有增益,他分组之后复杂度应该近似下图:
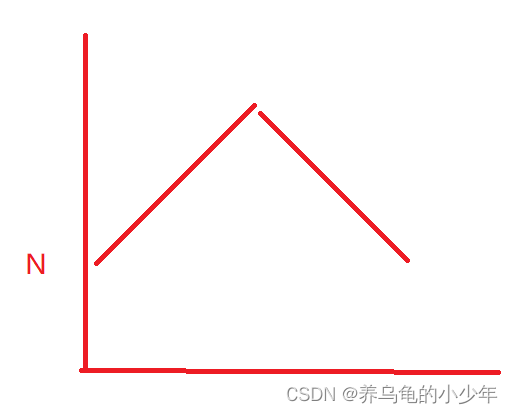
所以,虽然希尔的时间复杂度近似在N*logN这个等级,但是要比其大一点,查阅相关资料,对于希尔时间复杂度,通常是这么说的

2.2选择排序
2.2.1基本思想:
每一次从待排序的数据元素中选出最小(或最大)的一个元素,存放在序列的起始位置,直到全部待排序的数据元素排完 。
2.2.2直接选择排序
在元素集合array[i]--array[n-1]中选择关键码最大(小)的数据元素
若它不是这组元素中的最后一个(第一个)元素,则将它与这组元素中的最后一个(第一个)元素交换在剩余的array[i]--array[n-2](array[i+1]--array[n-1])集合中,重复上述步骤,直到集合剩余1个元素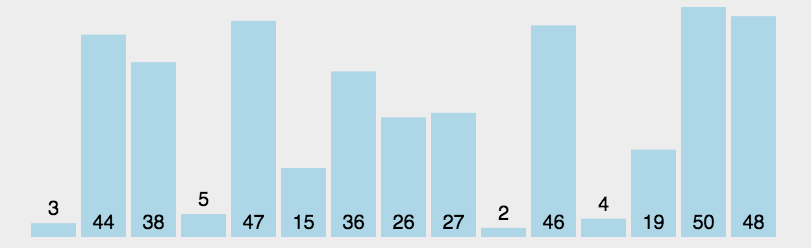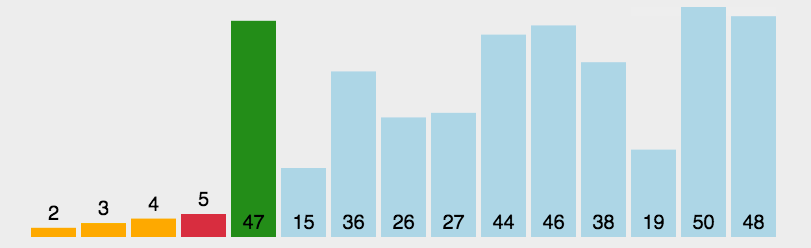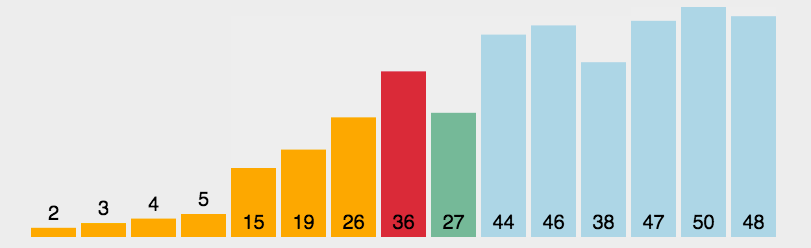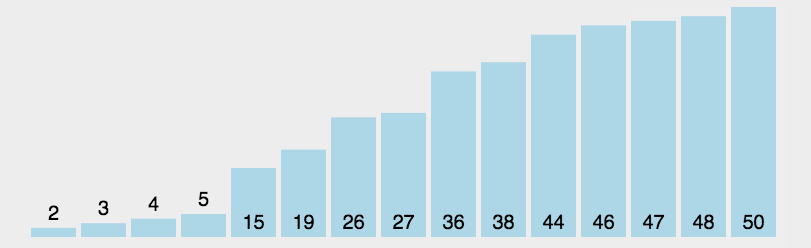
直接选择排序单趟寻找到最大的或最小的,实现升序的话就与最左边的交换,降序就与最右边交换,我们可以用代码实现左右共同查找的方式。如下所示:
void SelectSort(int* a, int n)
{//初试状态int left = 0;int right = n - 1;while (left < right){//取最小值,最大值下标为最左边的 位置int min = left, max = left;for (int i = left + 1; i < right; i++){if (a[i] < a[min]){min = i;}else if (a[i] > a[max]){max = i;}}swap(&a[left], &a[min]);if (left == max) //防止出现 left位置上放的是最大值{max = min;}swap(&a[right], &a[max]);left++;right--;}
}结果分析:
选择排序的时间复杂度,还是比较low的不管怎么选,都是O(N^2) 。
2.2.3堆排序
堆排序是我们的老朋友了,堆排序(Heapsort)是指利用堆积树(堆)这种数据结构所设计的一种排序算法,它是选择排序的一种。它是通过堆来进行选择数据。需要注意的是排升序要建大堆,排降序建小堆。
代码如下:
//向下调整
void AjustDown(int* a, int n, int parent)
{int child = parent * 2 + 1; //孩子和父亲的关系while (child < n) // 遍历条件{if (child + 1 < n && a[child + 1] > a[child]) //左右孩子 选择最大的那个,同时兼顾 右孩子也要小于边界{++child;}if (a[child] > a[parent]) // 建大堆{swap(&a[child], &a[parent]);parent = child;child = parent * 2 + 1;}else{break;}}}
void HeapSort(int* a, int n)
{for (int i = (n - 1 - 1) / 2; i >= 0; i--) // 从最后一个节点的父亲 开始向下调整 保证父亲比孩子大{AjustDown(a, n, i);}int end = n - 1;while (end > 0){swap(&a[end], &a[0]); // 交换 根节点 和最后一个位置的数值AjustDown(a, end, 0);--end;}
}总结:
堆排的时间复杂度 ,我们在堆排序那个章节推过,这里我直接说结论:o(N * logN)。
相关文章:

数据结构-排序
本节目标: 1.排序的概念及其运用 2.常见排序算法的实现 3.排序算法复杂度及稳定性分析 1.排序的概念及其应用 1.1排序的概念 排序就是按照某个我们设定的关键字,或者关键词,递增或者递减,完成这样的操作就是排序。 1.2排…...

ROS话题通信自定义+发布订阅代码--03
话题通信自定义msg 在 ROS 通信协议中,数据载体是一个较为重要组成部分,ROS 中通过 std_msgs 封装了一些原生的数据类型,比如:String、Int32、Int64、Char、Bool、Empty… 但是,这些数据一般只包含一个 data 字段,结构的单一意味…...

【MySQL】实验七 视图
文章目录 1. 建立city值为上海、北京的顾客视图2. 建立城市为上海的客户2016年的订单信息视图3. SQL视图:建立视图AVG_CJ4. SQL视图:建立视图IS_STUDENT5. SQL视图:建立视图CJ_STUDENT6. SQL视图:根据视图CJ_STUDENT创建视图CJ_TJ1. 建立city值为上海、北京的顾客视图 建立…...

Linux常见操作命令【三】
一、系统资源 1.1 ps(process staus) ps -ef e显示所有进程、f全格式 ps -aux 显示所有包含其他使用者的进程 ps -ef | grep CCC 查找含有CCC进程的格式 ps -u username 显示指定进程用户信息1.2 kill kill 12345 杀死进程12345 kill -KILL…...

C-关键字(下)
文章目录循环控制switch-case-break-defaultdo-while-forgetchar()break-continuegotovoidvoid*returnconstconst修饰变量const修饰数组const修饰指针指针补充const 修饰返回值volatilestruct柔型数组union联合体联合体空间开辟问题利用联合体的性质,判断机器是大端还是小端enu…...
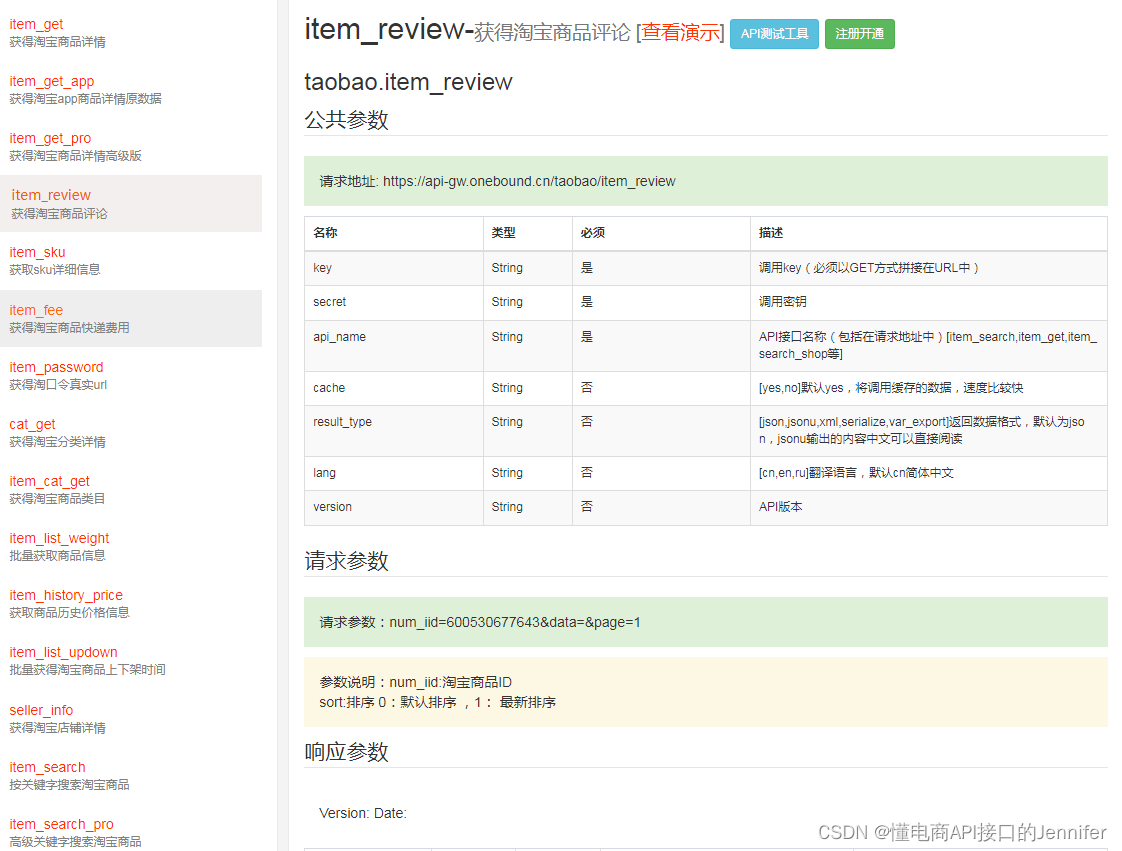
关于电商商品数据API接口列表,你想知道的(详情页、Sku信息、商品描述、评论问答列表)
目录 一、商品数据API接口列表 二、商品详情数据API调用代码item_get 三、获取sku详细信息item_sku 四、获得淘宝商品评论item_review 五、数据说明文档 进入 一、商品数据API接口列表 二、商品详情数据API调用代码item_get <?php// 请求示例 url 默认请求参数已经URL…...

232:vue+openlayers选择左右两部分的地图,不重复,横向卷帘
第232个 点击查看专栏目录 本示例的目的是介绍演示如何在vue+openlayers项目中自定义js实现横向卷帘。这个示例中从左右两个选择框中来选择不同的地图,做了不重复的处理,即同一个数组,两部分根据选择后的状态做disabled处理,避免重复选择。 直接复制下面的 vue+openlayers…...
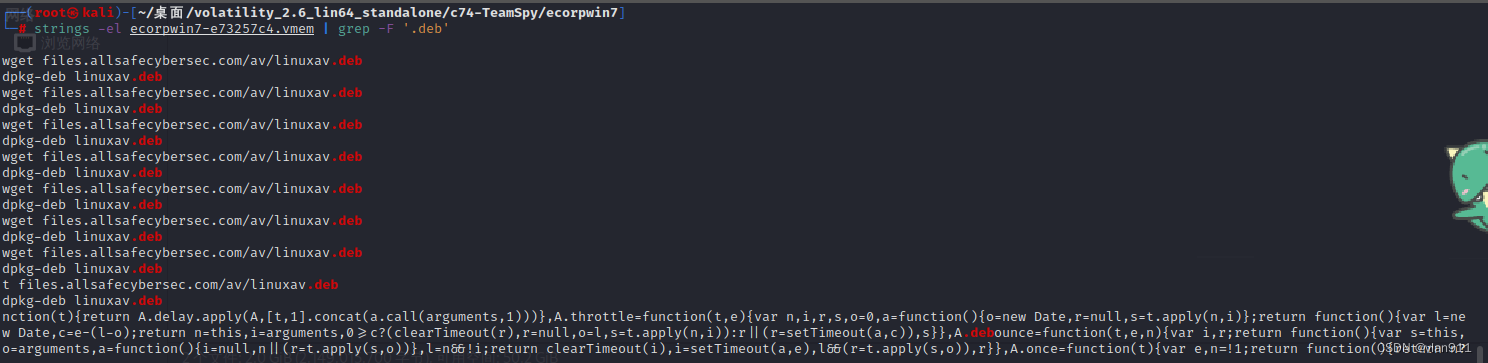
溯源取证-内存取证 高难度篇
今天的场景依然是windows场景,只不过此次场景分为两个镜像,本次学习主要学习如何晒别钓鱼邮件、如何提取钓鱼邮件、如何修复损坏的恶意文件、如何提取DLL动态链接库文件 本次需要使用的工具: volatility_2.6_lin64_standalone readpst clams…...

JAVA语言中的代理模式
代理可以进一步划分为静态代理和动态代理,代理模式在实际的生活中场景很多,例如中介、律师、代购等行业,都是简单的代理逻辑,在这个模式下存在两个关键角色: 目标对象角色:即代理对象所代表的对象。 代理…...

最后一步:渲染和绘制
浏览器的工作步骤如下: URL>字符流>词(token)流>DOM树(不含样式信息的 DOM)>DOM树CSS规则(含样式信息的 DOM)>根据样式信息,计算了每个元素的位置和大小>根据这些…...
C++类和对象终章——友元函数 | 友元类 | 内部类 | 匿名对象 | 关于拷贝对象时一些编译器优化
文章目录💐专栏导读💐文章导读🌷友元🌺概念🌺友元函数🍁友元函数的重要性质🌺友元类🍁友元类的重要性质🌷内部类(不常用)🌺内部类的性…...

拼多多按关键字搜索商品 API
一、拼多多平台优势: 1、独创拼团模式 拼团拼单是拼多多独创的营销模式,其特点是基于人脉社交的裂变传播,非常具有传播性。 由于本身走低价路线,加上拼单折扣,商品的分享和人群裂变效果非常明显,电商前期…...

全链路日志追踪
背景 最近线上的日志全局追踪 traceId 不好使了,不同请求经常出现重复的 traceId,或者通过某个请求的 traceId 追踪搜索,检索出了与该请求完全不相干的日志。我领导叫我去排查解决这个问题,这里我把我排查的过程思路以及如何解决…...
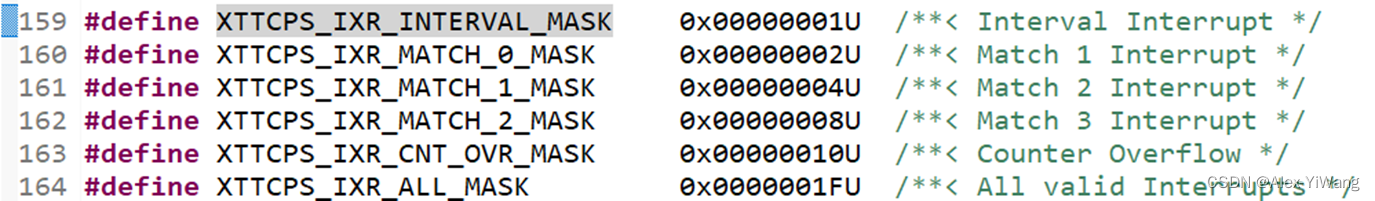
ZYNQ:【1】深入理解PS端的TTC定时器(Part1:原理+官方案例讲解)
碎碎念:好久不见,甚是想念!本期带来的是有关ZYNQ7020的内容,我们知道ZYNQ作为一款具有硬核的SOC,PS端很强大,可以更加便捷地实现一些算法验证。本文具体讲解一下里面的TTC定时器,之后发布的Part…...

蓝牙设备如何自定义UUID
如何自定义UUID 所有 BLE 自定义服务和特性必须使用 128 位 UUID 来识别,并且要确保基本 UUID 与 BLE 定义的基本 UUID(00000000-0000-1000-8000-00805F9B34FB)不一样。基本 UUID 是一个 128 位的数值,根据该值可定义标准UUID&am…...
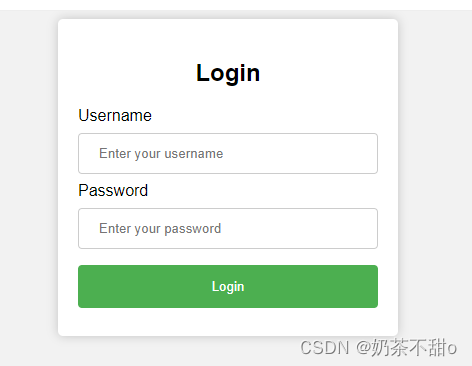
好看的html登录界面,
界面效果: 代码: <!DOCTYPE html> <html><head><title>Login Page</title><style>body {background-color: #f2f2f2;font-family: Arial, sans-serif;}form {background-color: #fff;border-radius: 5px;box-shado…...

Java模拟星空
目录 前言 JavaFX基础 1. GraphicsContext 2. AnimationTimer 代码实现 完整代码 前言 看了Python模拟星空很漂亮,Java也应该必须有一个! 环境:只需要JDK1.8就好!不需要外部包!!! Jav…...

YGG 代表 Web3 Gaming 参加 2023 年游戏开发者大会
Yield Guild Games(YGG)在 2023 年 3 月 20 日至 24 日在加州旧金山举行的游戏开发者大会(GDC)上大显身手,这是游戏开发者的重要交流学习活动。虽然 GDC 本身提供了多种多样的活动,包括讲座、小组讨论、圆桌…...

水库安全运行智慧管理平台解决方案筑牢防汛“安全墙”
解决方案 水库安全运行智慧管理系统解决方案,系统主要由降雨量监测站、水库水位监测站、大坝安全监测中的渗流量、渗流压力和变形监测站及视频和图像监测站等站点组成,同时建立规范、统一的监测平台,集数据传输、信息共享、数据储存于一体&a…...

Exchange升级部署方案
目录 前言 一、需求分析 二、升级前准备 1.备份当前 Exchange Server 数据...

LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器的上位机配置操作说明
LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器专为工业环境精心打造,完美适配AGV和无人叉车。同时,集成以太网与语音合成技术,为各类高级系统(如MES、调度系统、库位管理、立库等)提供高效便捷的语音交互体验。 L…...

Cursor实现用excel数据填充word模版的方法
cursor主页:https://www.cursor.com/ 任务目标:把excel格式的数据里的单元格,按照某一个固定模版填充到word中 文章目录 注意事项逐步生成程序1. 确定格式2. 调试程序 注意事项 直接给一个excel文件和最终呈现的word文件的示例,…...

智慧工地云平台源码,基于微服务架构+Java+Spring Cloud +UniApp +MySql
智慧工地管理云平台系统,智慧工地全套源码,java版智慧工地源码,支持PC端、大屏端、移动端。 智慧工地聚焦建筑行业的市场需求,提供“平台网络终端”的整体解决方案,提供劳务管理、视频管理、智能监测、绿色施工、安全管…...

spring:实例工厂方法获取bean
spring处理使用静态工厂方法获取bean实例,也可以通过实例工厂方法获取bean实例。 实例工厂方法步骤如下: 定义实例工厂类(Java代码),定义实例工厂(xml),定义调用实例工厂ÿ…...

【android bluetooth 框架分析 04】【bt-framework 层详解 1】【BluetoothProperties介绍】
1. BluetoothProperties介绍 libsysprop/srcs/android/sysprop/BluetoothProperties.sysprop BluetoothProperties.sysprop 是 Android AOSP 中的一种 系统属性定义文件(System Property Definition File),用于声明和管理 Bluetooth 模块相…...

如何在最短时间内提升打ctf(web)的水平?
刚刚刷完2遍 bugku 的 web 题,前来答题。 每个人对刷题理解是不同,有的人是看了writeup就等于刷了,有的人是收藏了writeup就等于刷了,有的人是跟着writeup做了一遍就等于刷了,还有的人是独立思考做了一遍就等于刷了。…...

佰力博科技与您探讨热释电测量的几种方法
热释电的测量主要涉及热释电系数的测定,这是表征热释电材料性能的重要参数。热释电系数的测量方法主要包括静态法、动态法和积分电荷法。其中,积分电荷法最为常用,其原理是通过测量在电容器上积累的热释电电荷,从而确定热释电系数…...

技术栈RabbitMq的介绍和使用
目录 1. 什么是消息队列?2. 消息队列的优点3. RabbitMQ 消息队列概述4. RabbitMQ 安装5. Exchange 四种类型5.1 direct 精准匹配5.2 fanout 广播5.3 topic 正则匹配 6. RabbitMQ 队列模式6.1 简单队列模式6.2 工作队列模式6.3 发布/订阅模式6.4 路由模式6.5 主题模式…...

腾讯云V3签名
想要接入腾讯云的Api,必然先按其文档计算出所要求的签名。 之前也调用过腾讯云的接口,但总是卡在签名这一步,最后放弃选择SDK,这次终于自己代码实现。 可能腾讯云翻新了接口文档,现在阅读起来,清晰了很多&…...

深入理解 React 样式方案
React 的样式方案较多,在应用开发初期,开发者需要根据项目业务具体情况选择对应样式方案。React 样式方案主要有: 1. 内联样式 2. module css 3. css in js 4. tailwind css 这些方案中,均有各自的优势和缺点。 1. 方案优劣势 1. 内联样式: 简单直观,适合动态样式和…...
