【剑指 offer】旋转数组的最小数字

✨个人主页:bit me👇
✨当前专栏:算法训练营👇
旋 转 数 组 的 最 小 数 字
| 核心考点:数组理解,二分查找,临界条件 |
描述:
有一个长度为 n 的非降序数组,比如[1,2,3,4,5],将它进行旋转,即把一个数组最开始的若干个元素搬到数组的末尾,变成一个旋转数组,比如变成了[3,4,5,1,2],或者[4,5,1,2,3]这样的。请问,给定这样一个旋转数组,求数组中的最小值。给出的所有元素都大于0,若数组大小为0,请返回0。
数据范围:
1 ≤ n ≤ 10000,数组中任意元素的值: 0 ≤ val ≤ 10000
要求:
- 空间复杂度:O(1)
- 时间复杂度:O(logn)
示例1:
输入:[3,4,5,1,2]
返回值:1
示例2:
输入:[3,100,200,3]
返回值:3
思路:
- 第一种方法:此题就是寻找最小值,最容易普遍的一种思路就是直接遍历,因为是非递减的,所以最小值可能出现在任何一个地方,但是注意,旋转有种特性,旋转之后,有可能出现递减,那么引起递减的第一个数字肯定就是我们要找的最小值。
- 第二种方法:由于第一种方法效率比较低下,思路也不够新颖,在我们提到查找的时候,就该想到 " 查找的本质是排除 " 这句话。采用二分查找!因为是旋转非递减数组,所以可以把整个数组分为两半,mid 是中间二分的值,left 是最左边的值,right 是最右边的值,当我们的 mid 值大于 left 值的时候,就说明 mid 处于原始数组前半部分,根据非递减的特性,就说明目标最小值在 mid 的右侧,然后让 left = mid 之后继续进行二分查找,直到找到为止;反之,当我们的 mid 值小于 left 值的时候,就说明 mid 处于原始数组后半部分,根据非递减的特性,就说明目标最小值在 mid 的左侧,然后让 right = mid 之后继续进行二分查找,直到找到为止。
- 注意非递减:所以有递增和相等两种可能,分别处理即可
第一种方法:
import java.util.ArrayList;
public class Solution {public int minNumberInRotateArray(int [] array) {if(array == null || array.length == 0){return 0;}for(int i = 0; i < array.length-1; i++){if(array[i] > array[i+1]){return array[i+1];}}return array[0];}
}
第二种方法:
- 先处理特殊情况,数组为空或者长度为 0 的时候
if(array == null || array.length == 0){return 0;
}
- 定义左右端点和中间值
int left = 0;
int right = array.length -1;
int mid = 0;
- 二分要循环进行查找,那么就要需要一个条件,条件就是 left < right
while(left < right){//...
}
- 后续代码在循环中完善,先考虑特殊情况,数组只有一个元素的时候
if(right - left == 1){mid = right;break;
}
- 非递减除了递增就还有左右端和中间值三个元素一样的情况
if(array[left] == array[right] && array[mid] == array[left]){int result = array[left];for(int i = left + 1; i < right; i++){if(result > array[i]){result = array[i];}}return result;
}
在这里我们就进行线性查找,依次遍历比较大小即可
- 中间值和左右端点进行比较直到找到为止
mid = (right + left) >> 1;
if(array[mid] >= array[left]){left = mid;
}else{right = mid;
}
总的代码:
import java.util.ArrayList;
public class Solution {public int minNumberInRotateArray(int [] array) {if(array == null || array.length == 0){return 0;}int left = 0;int right = array.length -1;int mid = 0;while(left < right){if(right - left == 1){mid = right;break;}//线性查找if(array[left] == array[right] && array[mid] == array[left]){int result = array[left];for(int i = left + 1; i < right; i++){if(result > array[i]){result = array[i];}}return result;}mid = (right + left) >> 1;if(array[mid] >= array[left]){left = mid;}else{right = mid;}}return array[mid];}
}
相关文章:

【剑指 offer】旋转数组的最小数字
✨个人主页:bit me👇 ✨当前专栏:算法训练营👇 旋 转 数 组 的 最 小 数 字核心考点:数组理解,二分查找,临界条件 描述: 有一个长度为 n 的非降序数组,比如[1,2,3,4,5]…...

GB 9706.1-2020 医用电气设备第1部分:基本安全和基本性能的通用要求-1
这是份什么文件 这是一份中华人民共和国国家标准,具体为GB9706.1—2020,标准适用于医用电气设备,并规定了医用电气设备基本安全和基本性能的通用要求。主要涵盖了医疗电器设备与患者接触的各种要求,包括电气安全、机械防护、防护辐…...
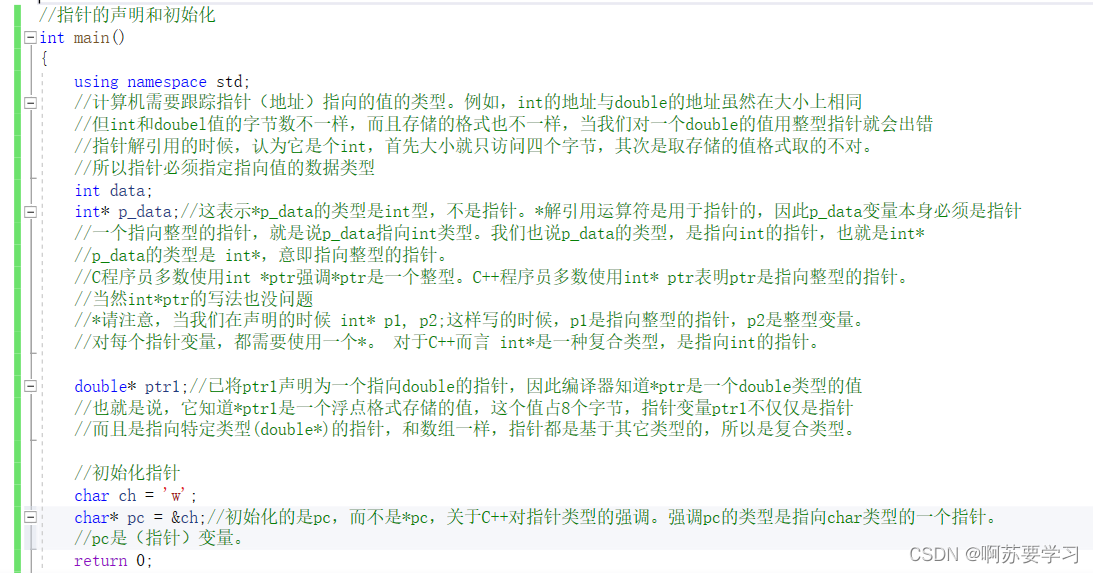
认识C++《共、枚、指1》
目录 前言: 1.共用体的基本知识 2.匿名共用体 3.枚举 3.1设置枚举值 3.2枚举的应用场景 3.3枚举变量的取值范围 4.地址和自由存储空间 5.指针的思想 6.指针的声明和初始化 前言: 指针内容比较多,还需要再出一篇。久等了!!我看了我的…...

vim 一键配置
PS:本文是为了以后为了方便,做备忘的,今天用的时候找了半天很麻烦。 vim编辑器一键配置 在非root用户下执行上面的语句即可,不要在root用户下直接安装! 安装的时候需要输入root用户的密码,请找您的服主要一…...

如何成为一名成功的 PHP 开发者
当今的网络应用开发市场,PHP 一直是其中最受欢迎的语言之一,许多优秀的网络应用程序都是由 PHP 开发人员设计和开发的。如果你想成为一名成功的 PHP 开发者,以下是几个关键步骤: 1. 学习基础知识 首先,你需要掌握 PH…...
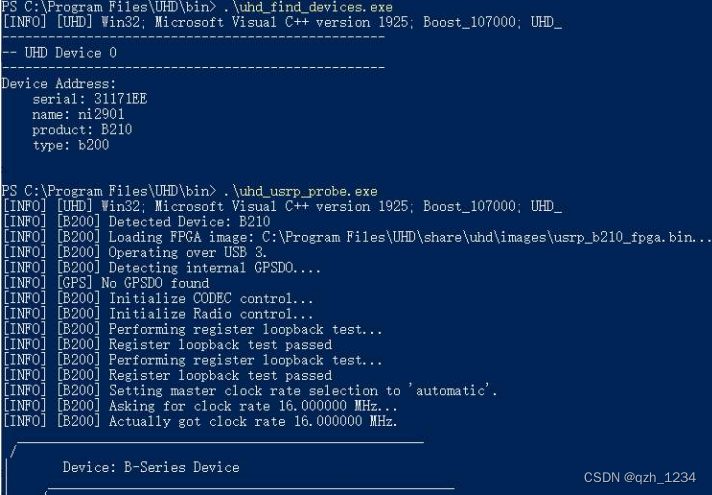
UHD安装教程
UHD Universal Hardware Driver,即USRP驱动。 UHD,Windows平台安装教程 uhd驱动安装 http://files.ettus.com/binaries/misc/erllc_uhd_winusb_driver.zip 安装LibUSBx http://files.ettus.com/binaries/uhd/latest_release 下载默认C盘 环境配置 将…...

Unity和UE有啥区别?哪个更适合游戏开发
游戏制作软件中最著名的两个游戏引擎是 Unity 和 Unreal Engine。从独立游戏到大型工作室,许多游戏开发商都在使用它们。如果你打算从事游戏行业工作,你肯定曾经问过自己“我的游戏应该使用 Unity 还是 Unreal Engine?” ” 让我们来了解和比…...
红队内网靶场
文章目录开篇介绍靶场介绍靶场下载以及配置Tomcat Get Shell突破DMZ防火墙拿下域内成员机器将内网机器上线到CS使用Adfind侦察子域信息控制子域DCRadmin登录子域进行权限维持(白银票据/ACL)子域bloodhound获取父域信息分析子域Krbtgt密钥创建跨域金票Dcsync父域PTH父域DC准备打…...

如何合并多个升序链表?
前言 本文主要介绍如何将多个小的升序链表合并一个大的升序链表。 需求描述 给出K个升序链接,要求把这K个升序链表合并成一个,并且这个链表也是升序的。 例如:A [1,5,6], B [2,3,8], C [4,4,9] 将这3个链表合并成一个链表D…...

23上半年信息系统项目管理师新老教程兼顾使用备考策略
在离考试仅有50多天的时候,软考办发文:“为方便报考信息系统项目管理师的考生进行复习备考,2023年上半年信息系统项目管理师考试第3版、第4版教程兼顾使用”。 其实软考办发布这样一条信息,也是为了照顾那些在新版发布以前按第…...
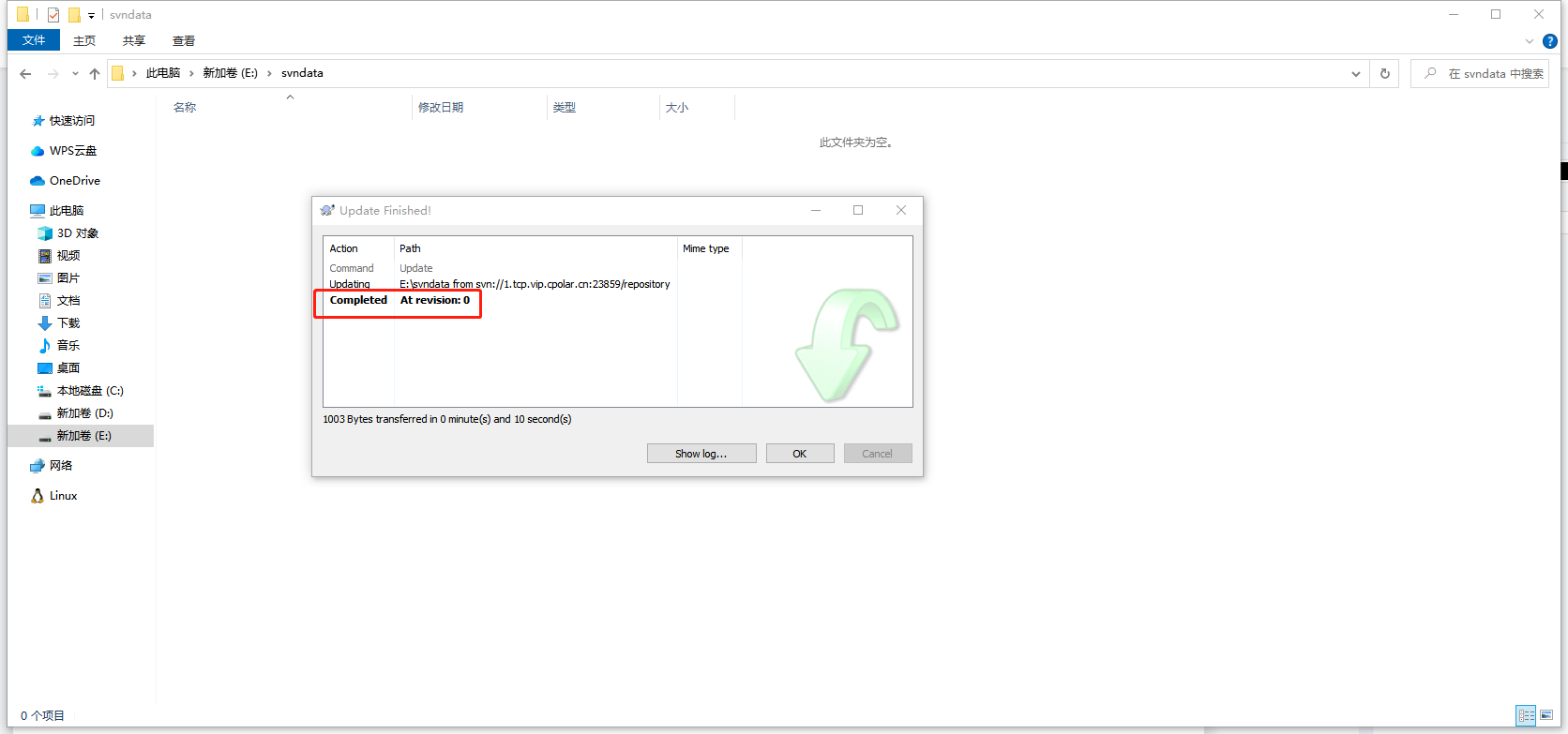
Linux环境搭建SVN服务器并实现公网访问 - cpolar端口映射
文章目录前言1. Ubuntu安装SVN服务2. 修改配置文件2.1 修改svnserve.conf文件2.2 修改passwd文件2.3 修改authz文件3. 启动svn服务4. 内网穿透4.1 安装cpolar内网穿透4.2 创建隧道映射本地端口5. 测试公网访问6. 配置固定公网TCP端口地址6.1 保留一个固定的公网TCP端口地址6.2 …...
)
仿牛客网社区Web开发项目代码逐行精读(更新中)
仿牛客网社区Web开发项目怎么看项目?如何调试项目前瞻技术架构项目亮点开始看代码LoginControllerDiscussPostController怎么看项目? pom.xml看技术架构resource看配置文件,这个项目是前后端不分离的以调试为导向,从前端入手检查…...
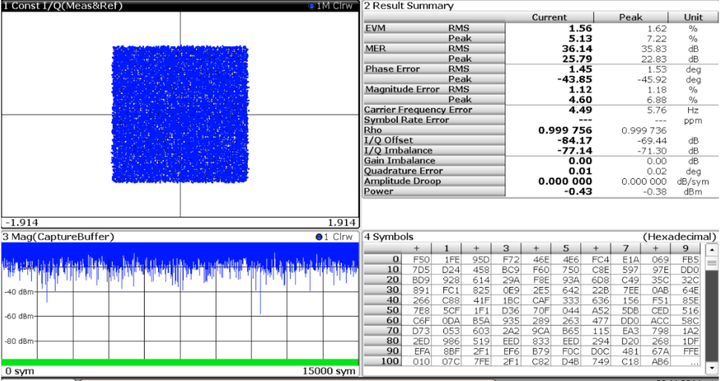
5G NR调制阶数与EVM关系以及对系统SNR要求分析
移动通信技术对数据传输速率要求越来越高。一种提高传输速率的思路是使用更高阶的QAM 调制方式,例如5G NR 的256QAM PDSCH,微波的1024QAM,2048QAM和4096QAM 调制。更高阶的QAM 调制方式对系统也提出了更高的要求。例如某个系统的EVM 测试结果…...
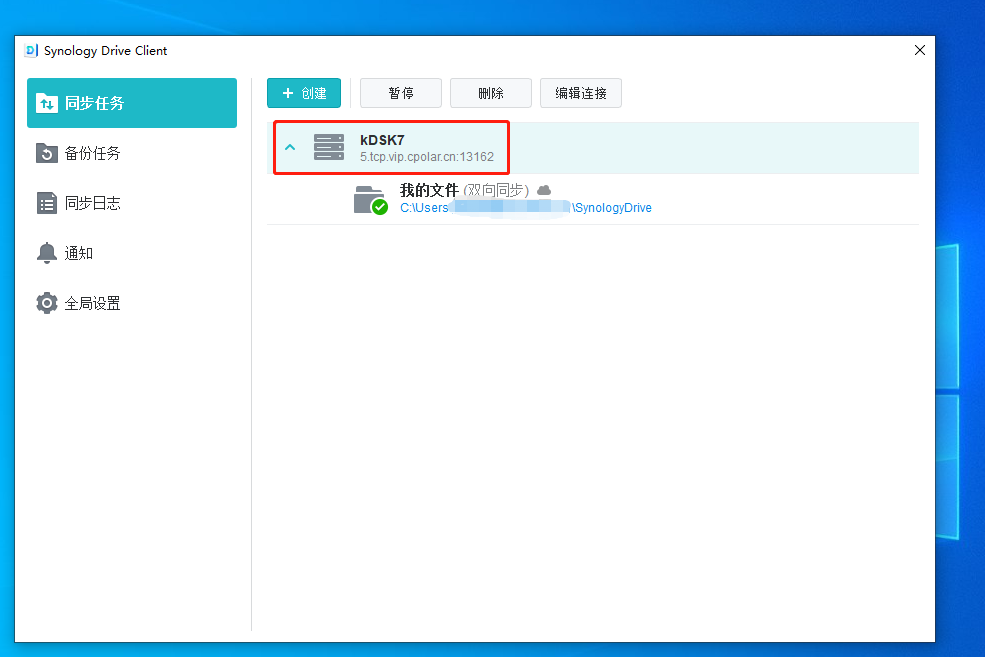
【NAS群晖drive异地访问】远程连接drive挂载电脑硬盘「内网穿透」
文章目录前言1.群晖Synology Drive套件的安装1.1 安装Synology Drive套件1.2 设置Synology Drive套件1.3 局域网内电脑测试和使用2.使用cpolar远程访问内网Synology Drive2.1 Cpolar云端设置2.2 Cpolar本地设置2.3 测试和使用3. 结语转发自CSDN远程穿透的文章:【群晖…...

react:hooks为什么不能写在条件语句里
背景 最近朋友在面试,说面试官问到了一个问题不会,说为什么 react hooks为什么不能写在条件语句里,今天我们来研究一下这个问题。 我们在来简单实现一个 useState: const reRender () > {stateIndex -1 ReactDOM.render(&…...

模型优势缺陷整理
(1)BERT 1. 计算资源消耗:bert模型是一个相对较大的模型,具有数亿个参数。因此,为了训练和使用bert模型,需要大量的计算资源和时间。 2. 学习不足问题:尽管bert模型在大规模语料库上进行了预训…...
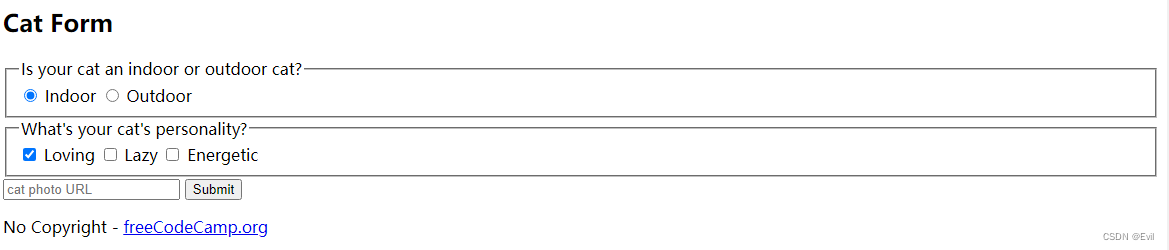
编写猫咪相册应用 HTML
文章目录1. 标题元素标签2. p元素用于在网站上创建一段文本3. 注释4. 页面主要部分标识标签5. 通过使用img元素来为你的网站添加图片6. 使用锚点元素(a)链接到另一个页面7. 使用 section 元素将照片内容与未来的内容分开8. 无序列表(ul)元素,列表项(li)元素在列表中…...

基于Arduino与LabVIEW的远程家庭监控系统
在基于Arduino与LabVIEW的远程家庭监控系统中,Arduino Uno控制器需要完成以下功能:1)通过W5100网络模块接收并判断命令,采集和传输温度、煤气浓度、热释电传感器的数据,并通过W5100网络模块上传给LabVIEW软件。2&#…...

使用FRP(快速反向代理)实现内网穿透——以腾讯云服务器为例
一、FRP简介 FRP,即快速反向代理技术(fast reverse proxy)。本文的FRP程序是基于github开源项目GitHub - fatedier/frp。当前,该程序可实现:“将位于 NAT 或防火墙后面的本地服务器暴露给互联网”。它目前支持 TCP 和…...

d跨语言链接优化
原文 使用LDC的(LTO)链接时优化的简短文章,包含演示了如何提高程序性能的简单示例.因为LTO在LLVMIR级别工作,因此可跨越C/D语言优化! 重要提示:LDC/LLVM的LTO在窗口上不可用. 链接时优化 (LTO)链接时优化是指链接时的程序优化.链接器提取所有目标文件在一起,并合并到一个程序…...

AI-调查研究-01-正念冥想有用吗?对健康的影响及科学指南
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

【杂谈】-递归进化:人工智能的自我改进与监管挑战
递归进化:人工智能的自我改进与监管挑战 文章目录 递归进化:人工智能的自我改进与监管挑战1、自我改进型人工智能的崛起2、人工智能如何挑战人类监管?3、确保人工智能受控的策略4、人类在人工智能发展中的角色5、平衡自主性与控制力6、总结与…...

PHP和Node.js哪个更爽?
先说结论,rust完胜。 php:laravel,swoole,webman,最开始在苏宁的时候写了几年php,当时觉得php真的是世界上最好的语言,因为当初活在舒适圈里,不愿意跳出来,就好比当初活在…...

在rocky linux 9.5上在线安装 docker
前面是指南,后面是日志 sudo dnf config-manager --add-repo https://download.docker.com/linux/centos/docker-ce.repo sudo dnf install docker-ce docker-ce-cli containerd.io -y docker version sudo systemctl start docker sudo systemctl status docker …...

Qt Http Server模块功能及架构
Qt Http Server 是 Qt 6.0 中引入的一个新模块,它提供了一个轻量级的 HTTP 服务器实现,主要用于构建基于 HTTP 的应用程序和服务。 功能介绍: 主要功能 HTTP服务器功能: 支持 HTTP/1.1 协议 简单的请求/响应处理模型 支持 GET…...

Java-41 深入浅出 Spring - 声明式事务的支持 事务配置 XML模式 XML+注解模式
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

Robots.txt 文件
什么是robots.txt? robots.txt 是一个位于网站根目录下的文本文件(如:https://example.com/robots.txt),它用于指导网络爬虫(如搜索引擎的蜘蛛程序)如何抓取该网站的内容。这个文件遵循 Robots…...
)
相机Camera日志分析之三十一:高通Camx HAL十种流程基础分析关键字汇总(后续持续更新中)
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了:有对最普通的场景进行各个日志注释讲解,但相机场景太多,日志差异也巨大。后面将展示各种场景下的日志。 通过notepad++打开场景下的日志,通过下列分类关键字搜索,即可清晰的分析不同场景的相机运行流程差异…...

【分享】推荐一些办公小工具
1、PDF 在线转换 https://smallpdf.com/cn/pdf-tools 推荐理由:大部分的转换软件需要收费,要么功能不齐全,而开会员又用不了几次浪费钱,借用别人的又不安全。 这个网站它不需要登录或下载安装。而且提供的免费功能就能满足日常…...

jmeter聚合报告中参数详解
sample、average、min、max、90%line、95%line,99%line、Error错误率、吞吐量Thoughput、KB/sec每秒传输的数据量 sample(样本数) 表示测试中发送的请求数量,即测试执行了多少次请求。 单位,以个或者次数表示。 示例:…...
