程序设计方法学
体育竞技分析
问题分析
体育竞技分析
需求:毫厘是多少?
如何科学分析体育竞技比赛?
输入:球员的水平
输出:可预测的比赛成绩
体育竞技分析:模拟N场比赛
计算思维:抽象 + 自动化
模拟:抽象比赛过程 + 自动化执行N场比赛
当N越大时,比赛结果分析会越科学
比赛规则
双人击球比赛:A & B,回合制,5局3胜
开始时一方先发球,直至判分,接下来胜者发球
球员只能在发球局得分,15分胜一局
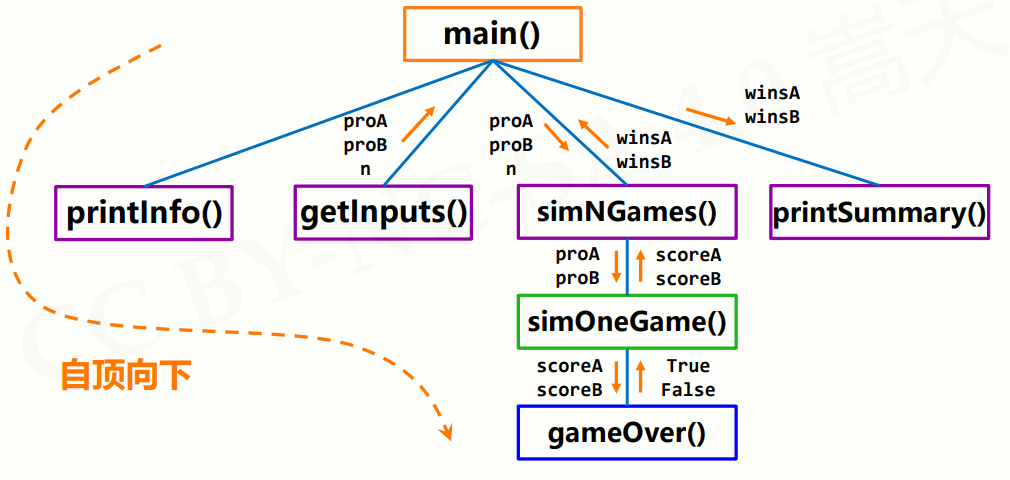
这要说到俩个概念,自顶向下的设计和自底向上的执行
自顶向下 解决复杂问题的有效方法
将一个总问题表达为若干个小问题组成的形式
使用同样方法进一步分解小问题
直至,小问题可以用计算机简单明了的解决
自底向上(执行)
逐步组建复杂系统的有效测试方法
分单元测试,逐步组装
按照自顶向下相反的路径操作
直至,系统各部分以组装的思路都经过测试和验证

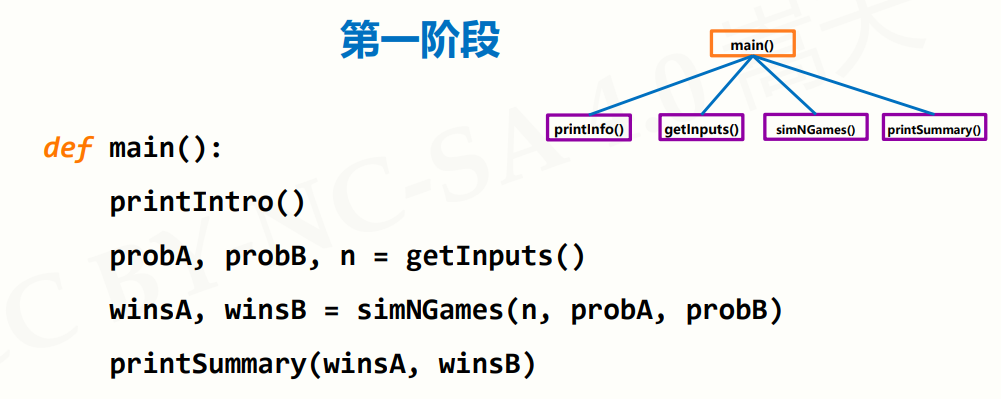





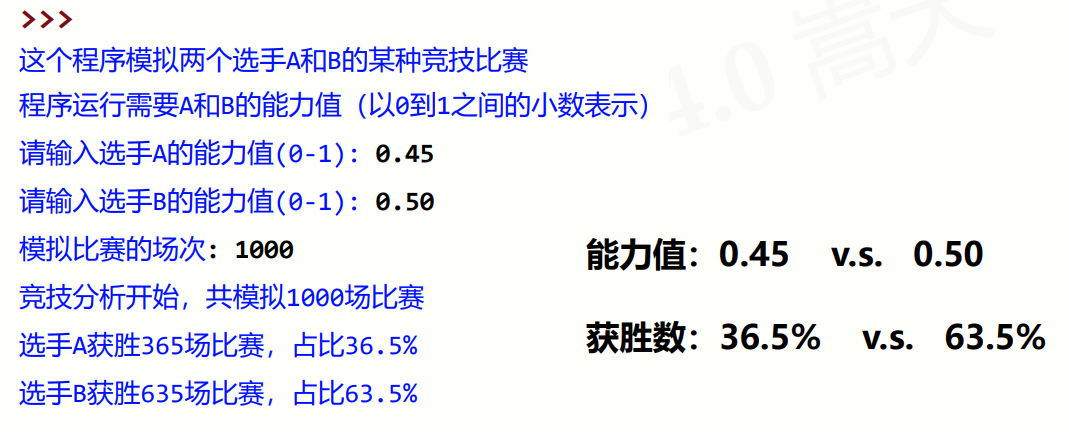
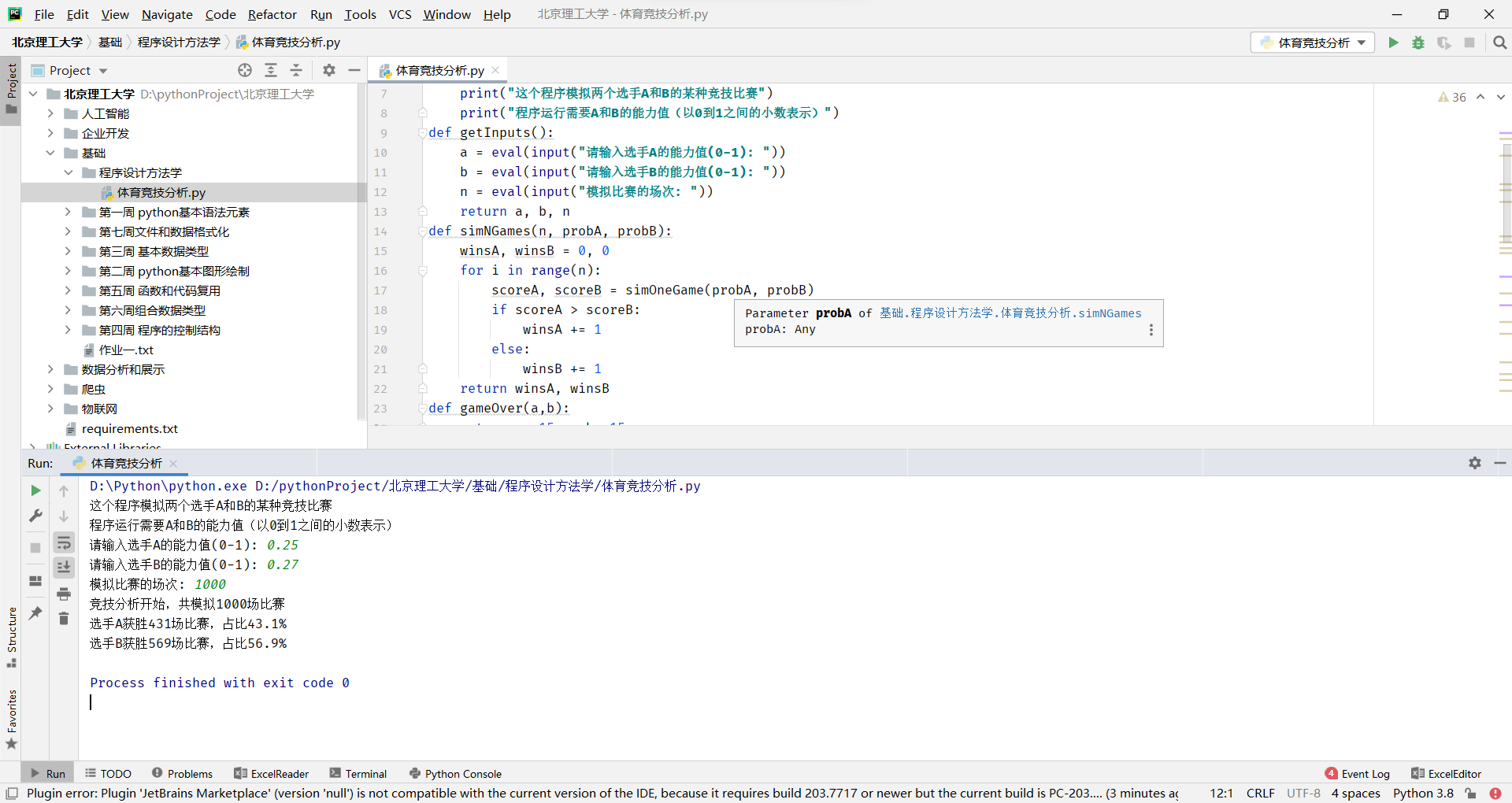
这是一个Python程序,用于模拟两个选手A和B进行某种竞技比赛的结果,并给出比赛结果的统计分析。
首先,程序定义了几个函数:
- printIntro():用于打印程序的简要介绍。
- getInputs():用于获取用户输入的选手A和B的能力值,以及模拟比赛的场次。
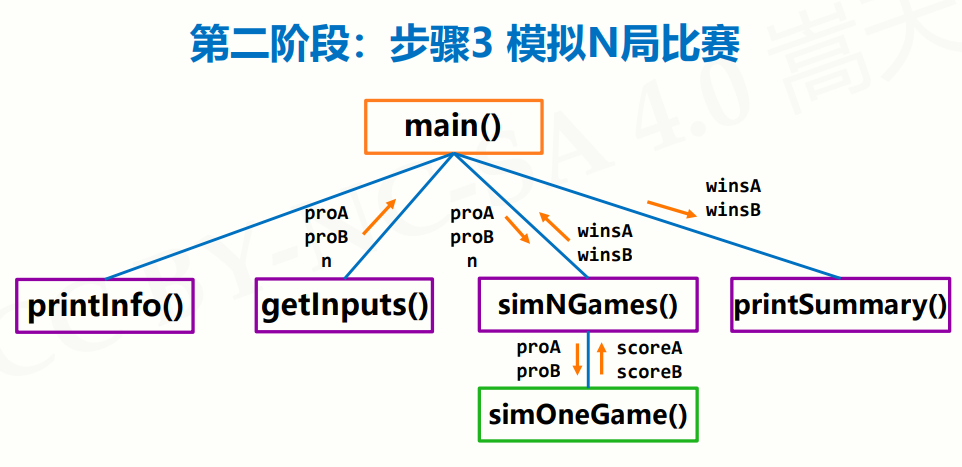
- simNGames(n, probA, probB):用于模拟n场比赛,并返回选手A和B的胜场数。
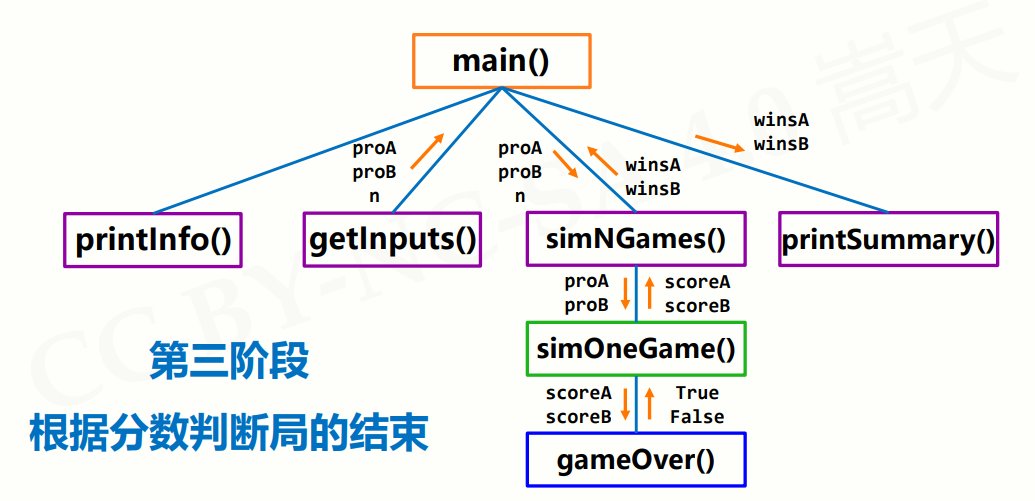
- gameOver(a,b):用于判断比赛是否结束,当选手A或B的得分达到15分时比赛结束。
- simOneGame(probA, probB):用于模拟一场比赛的结果,返回选手A和B的得分。
- printSummary(winsA, winsB):用于打印竞技分析结果,包括模拟比赛的场次、选手A和B的获胜场次及占比。
然后,程序调用main()函数,依次执行以下操作:
- 打印程序的简要介绍。
- 获取用户输入的选手A和B的能力值,以及模拟比赛的场次。
- 模拟n场比赛,并返回选手A和B的胜场数。
- 打印竞技分析结果,包括模拟比赛的场次、选手A和B的获胜场次及占比。
总体来说,该程序是一个简单的竞技分析模拟程序,通过随机数模拟比赛结果,并对比赛结果进行统计分析,得出选手A和B的胜率。
#!/usr/bin/env python
# -- coding: utf-8 --
# @Time : 2023/4/11 16:50
# @File : 体育竞技分析.py
from random import random
def printIntro():print("这个程序模拟两个选手A和B的某种竞技比赛")print("程序运行需要A和B的能力值(以0到1之间的小数表示)")
def getInputs():a = eval(input("请输入选手A的能力值(0-1): "))b = eval(input("请输入选手B的能力值(0-1): "))n = eval(input("模拟比赛的场次: "))return a, b, n
def simNGames(n, probA, probB):winsA, winsB = 0, 0for i in range(n):scoreA, scoreB = simOneGame(probA, probB)if scoreA > scoreB:winsA += 1else:winsB += 1return winsA, winsB
def gameOver(a,b):return a==15 or b==15
def simOneGame(probA, probB):scoreA, scoreB = 0, 0serving = "A"while not gameOver(scoreA, scoreB):if serving == "A":if random() < probA:scoreA += 1else:serving="B"else:if random() < probB:scoreB += 1else:serving="A"return scoreA, scoreB
def printSummary(winsA, winsB):n = winsA + winsBprint("竞技分析开始,共模拟{}场比赛".format(n))print("选手A获胜{}场比赛,占比{:0.1%}".format(winsA, winsA/n))print("选手B获胜{}场比赛,占比{:0.1%}".format(winsB, winsB/n))
def main():printIntro()probA, probB, n = getInputs()winsA, winsB = simNGames(n, probA, probB)printSummary(winsA, winsB)
main()python程序设计思维
计算思维与程序设计
第3种人类思维特征
逻辑思维:推理和演绎,数学为代表,A->B B->C A->C -
实证思维:实验和验证,物理为代表,引力波<-实验 -
计算思维:设计和构造,计算机为代表,汉诺塔递归
抽象和自动化
计算思维:Computational Thinking
抽象问题的计算过程,利用计算机自动化求解
计算思维是基于计算机的思维方式
 以前就是实证思维,通过查询当地的历史天气的数据,并且根据这样的经验,来猜测第二天的温度。实证思维通过物理,经验的东西来构造未来的值
以前就是实证思维,通过查询当地的历史天气的数据,并且根据这样的经验,来猜测第二天的温度。实证思维通过物理,经验的东西来构造未来的值
计算思维,就是通过计算机来演算天气,这样数据更加精确
计算生态与python语言

优质的计算生态Python123 - 编程更简单
用户体验与软件产品





应用开发的四个步骤


注:内容来自慕课--嵩天老师
相关文章:

程序设计方法学
体育竞技分析 问题分析 体育竞技分析 需求:毫厘是多少? 如何科学分析体育竞技比赛? 输入:球员的水平 输出:可预测的比赛成绩 体育竞技分析:模拟N场比赛 计算思维:抽象 自动化 模拟&am…...

Hadoop之Yarn篇
目录 编辑 Yarn的工作机制: 全流程作业: Yarn的调度器与调度算法: FIFO调度器(先进先出): 容量调度器(Capacity Scheduler): 容量调度器资源分配算法࿱…...

Spring Cloud Nacos使用总结
目录 安装Nacos服务器 服务发现与消费 服务发现与消费-添加依赖 服务发现-配置文件 服务发现-注解 服务发现-Controller 服务消费-配置文件 服务消费-注解与Ribbon消费代码 服务消费-运行 配置管理 配置管理-添加依赖 配置管理-配置文件 配置管理-注解 配置管理-…...

目标检测框架yolov5环境搭建
目前,目标检测框架中,yolov5 是很火的,它基于pytorch框架,集成opencv等框架,项目地址:https://github.com/ultralytics/yolov5,对我来说,机器学习、深度学习才开始接触,本…...
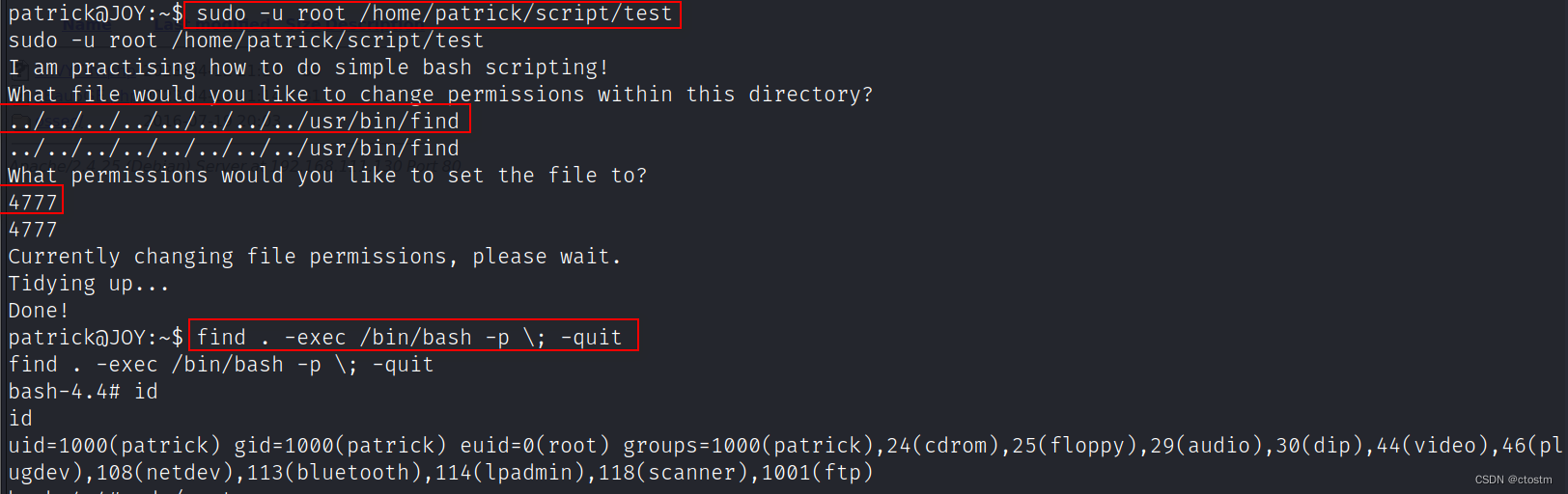
Vulnhub:Digitalworld.local (JOY)靶机
kali:192.168.111.111 靶机:192.168.111.130 信息收集 端口扫描 nmap -A -v -sV -T5 -p- --scripthttp-enum 192.168.111.130 使用enum4linux枚举目标smb服务,发现两个系统用户 enum4linux -a 192.168.111.130 ftp可以匿名登陆ÿ…...

STL源码剖析-六大部件, 部件的关系,复杂度, 区间表示
C标准库-体系结构与内核分析 根据源代码来分析 介绍 自学C侯捷老师的STL源码剖析的个人笔记,方便以后进行学习,查询。 为什么要学STL?按侯捷老师的话来说就是:使用一个东西,却不明白它的道理,不高明&…...

总有一个可用的连接,metaIPC1.2进入智能连接新时代
概述 metaIPC有1.0和2.0两个产品系列,2.0版本是可视对讲IPC,1.0新版本1.2在全面兼容ICE规范基础上进行了扩展,使metaIPC1.2进入智能化连接新时代。 metaIPC1.2在host/stun/turn/srs/zlm/janus/freeswitch等p2p/sfu/mcu进行全方位连通测试&a…...

棋盘问题c
在一个给定形状的棋盘(形状可能是不规则的)上面摆放棋子,棋子没有区别。要求摆放时任意的两个棋子不能放在棋盘中的同一行或者同一列,请编程求解对于给定形状和大小的棋盘,摆放k个棋子的所有可行的摆放方案C。 Input …...

华纳云:Linux系统下怎么创建普通用户并更改用户组
本篇内容主要讲解“Linux系统下怎么创建普通用户并更改用户组”,感兴趣的朋友不妨来看看。本文介绍的方法操作简单快捷,实用性强。下面就让小编来带大家学习“Linux系统下怎么创建普通用户并更改用户组”吧! 要求 项目做权限管理,不用root部…...

「她时代」背后的欧拉力量
2018年大热电视剧《北京女子图鉴》,讲述了一群在北京打拼的职业女性,她们背井离乡,被现实包裹,被压力、责任困扰,但依旧用倔强的个性、不屈的进取心和深厚的知识技能努力营造、交织出一片励志的天空,既激昂…...

kubespray v2.21.0 在线部署 kubernetes v1.24.0 集群【2】
文章目录创建 虚拟机模板虚拟机名称配置静态地址配置代理yum 配置配置主机名安装 git安装 docker安装 ansible配置内核参数安装 k8s定制安装新增节点配置主机名配置代理配置互信更新 inventory报错kubespray v2.21.0 部署 kubernetes v1.24.0 集群 【1】在 Rocky linux 8.7 使用…...

聚焦运营商信创运维,美信时代监控易四大亮点值得一试!
2021年11月《“十四五”信息通信行业发展规划》提出,到2025年,我国将建立高速泛在、集成互联、智能绿色、安全可靠的新型数字基础设施体系。 此《规划》让我国运营商信创进一步加速,中国移动、中国电信、中国联通等都先后加入信创大军&#x…...

[python刷题模板] 博弈入门-记忆化搜索/dp/打表
[python刷题模板] 博弈入门-记忆化搜索/dp/打表 一、 算法&数据结构1. 描述2. 复杂度分析3. 常见应用4. 常用优化二、 模板代码1. 打表贪心的博弈2. 464. 我能赢吗3. Nim游戏--最最基础版n1。三、其他四、更多例题五、参考链接一、 算法&数据结构 1. 描述 博弈一直没…...
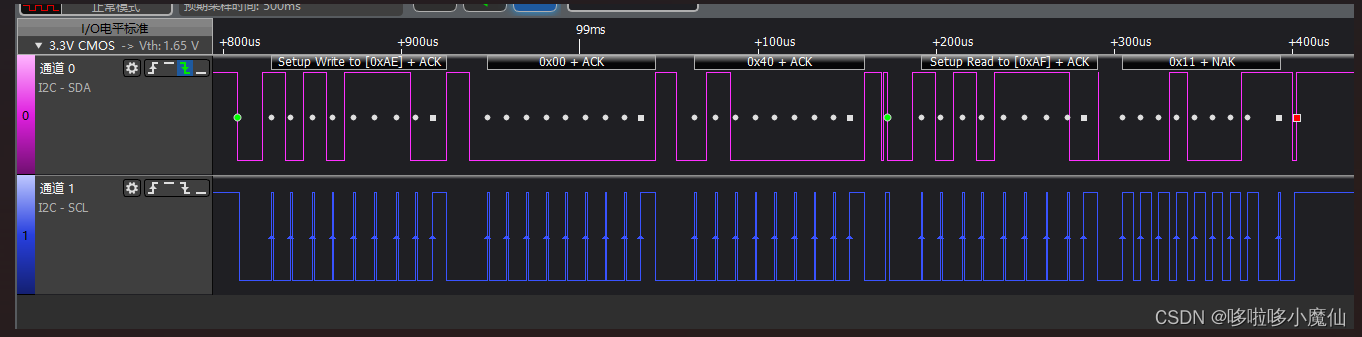
I2C通信
一、理论上了解I2C时序 I2C写数据时序如图: 通过解析器解析I2C通信如上图(SCL和SDA反了)。 1---起始信号 2、3---应答信号ACK 5---停止信号 起始信号:SCL线是高电平时,SDA线从高电平向低电平切换。 停…...
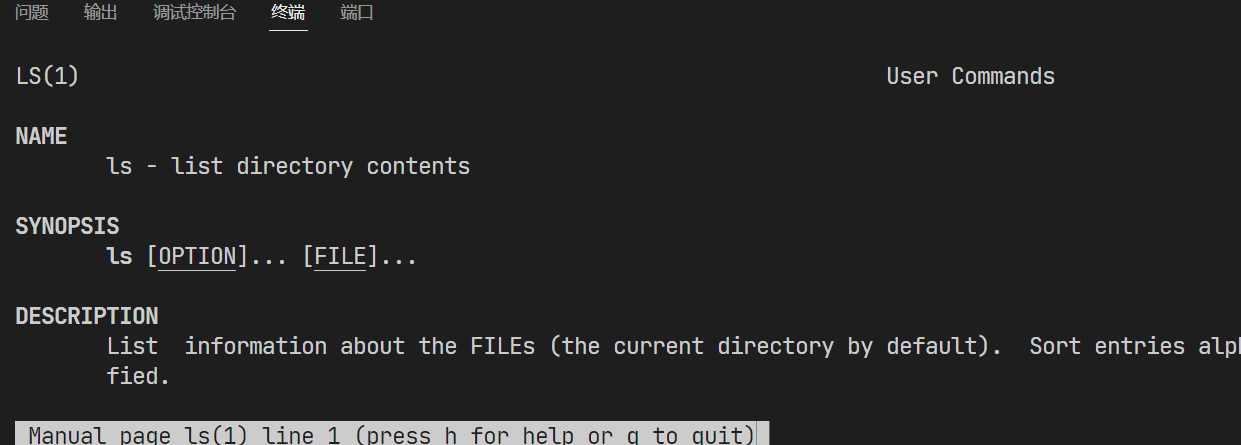
【Linux】man什么都搜不了,No manual entry for xxx的解决方案
本文首发于 慕雪的寒舍 man什么都搜不了,No manual entry for xxx的解决方案 系统 CentOS 7.6 1.问题描述 今天查手册的时候,发现man什么都查不了。不管是系统接口还是函数,都显示没有入口文档(No manual entry for)…...

STM32 库函数 GPIO_SetBits、GPIO_ResetBits、GPIO_WriteBit、GPIO_Write 区别
问题:当我使用STM32库函数对 I/O 口进行赋值时,在头文件中发现有四个相关的函数可以做这个操作,那么它们有什么区别呢? 一、GPIO_SetBits //eg: GPIO_SetBits(GPIOA, GPIO_Pin_1 | GPIO_Pin_2);解释:置位(置1)选择的数…...

在 RISC-V Linux 内核中添加模块
在 RISC-V Linux 内核中添加模块 flyfish 本例以添加helloworld字符设备为例 一 源码配置 1 源码 源码文件helloworld.c拷贝到 drivers/char 目录中 源码主要是输出Hello world init 2 Kconfig 打开drivers/char 目录下的Kconfig文件 在endmenu之前加上 config HELLO…...
利用AOP实现统一功能处理
目录 一、实现用户登录校验 实现自定义拦截器 将自定义的拦截器添加到框架的配置中,并且设置拦截的规则 二、实现统一异常处理 三、实现统一数据格式封装 一、实现用户登录校验 在之前的项目中,在需要验证用户登录的部分,每次都需要利…...

会话技巧---英文单词
目录 前言原文表示同意、答应表示不同意表示建议与忠告鼓励称赞担心与忧虑赞美夸奖-单词前言 加油 原文 表示同意、答应 1.agree[əˈgri]vi. 同意(=approve of); 答应(= consent to) agreement [əˈgrimənt] n. (意见或看法)一致 agree with sb about / on sth…...

VS中解决方案和项目的区别
总目录 文章目录总目录一、概述1、解决方案2、项目3、项目文件4、解决方案文件夹二、图解1、图解解决方案和项目的关系2、图解sln文件3、图解项目文件结语一、概述 1、解决方案 解决方案是一个容器,通常包含多个项目,这些项目通常相互引用。 解决方案中…...

KubeSphere 容器平台高可用:环境搭建与可视化操作指南
Linux_k8s篇 欢迎来到Linux的世界,看笔记好好学多敲多打,每个人都是大神! 题目:KubeSphere 容器平台高可用:环境搭建与可视化操作指南 版本号: 1.0,0 作者: 老王要学习 日期: 2025.06.05 适用环境: Ubuntu22 文档说…...

Chapter03-Authentication vulnerabilities
文章目录 1. 身份验证简介1.1 What is authentication1.2 difference between authentication and authorization1.3 身份验证机制失效的原因1.4 身份验证机制失效的影响 2. 基于登录功能的漏洞2.1 密码爆破2.2 用户名枚举2.3 有缺陷的暴力破解防护2.3.1 如果用户登录尝试失败次…...

【网络】每天掌握一个Linux命令 - iftop
在Linux系统中,iftop是网络管理的得力助手,能实时监控网络流量、连接情况等,帮助排查网络异常。接下来从多方面详细介绍它。 目录 【网络】每天掌握一个Linux命令 - iftop工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景…...

CVPR 2025 MIMO: 支持视觉指代和像素grounding 的医学视觉语言模型
CVPR 2025 | MIMO:支持视觉指代和像素对齐的医学视觉语言模型 论文信息 标题:MIMO: A medical vision language model with visual referring multimodal input and pixel grounding multimodal output作者:Yanyuan Chen, Dexuan Xu, Yu Hu…...

阿里云ACP云计算备考笔记 (5)——弹性伸缩
目录 第一章 概述 第二章 弹性伸缩简介 1、弹性伸缩 2、垂直伸缩 3、优势 4、应用场景 ① 无规律的业务量波动 ② 有规律的业务量波动 ③ 无明显业务量波动 ④ 混合型业务 ⑤ 消息通知 ⑥ 生命周期挂钩 ⑦ 自定义方式 ⑧ 滚的升级 5、使用限制 第三章 主要定义 …...

多场景 OkHttpClient 管理器 - Android 网络通信解决方案
下面是一个完整的 Android 实现,展示如何创建和管理多个 OkHttpClient 实例,分别用于长连接、普通 HTTP 请求和文件下载场景。 <?xml version"1.0" encoding"utf-8"?> <LinearLayout xmlns:android"http://schemas…...

转转集团旗下首家二手多品类循环仓店“超级转转”开业
6月9日,国内领先的循环经济企业转转集团旗下首家二手多品类循环仓店“超级转转”正式开业。 转转集团创始人兼CEO黄炜、转转循环时尚发起人朱珠、转转集团COO兼红布林CEO胡伟琨、王府井集团副总裁祝捷等出席了开业剪彩仪式。 据「TMT星球」了解,“超级…...

Neo4j 集群管理:原理、技术与最佳实践深度解析
Neo4j 的集群技术是其企业级高可用性、可扩展性和容错能力的核心。通过深入分析官方文档,本文将系统阐述其集群管理的核心原理、关键技术、实用技巧和行业最佳实践。 Neo4j 的 Causal Clustering 架构提供了一个强大而灵活的基石,用于构建高可用、可扩展且一致的图数据库服务…...

ip子接口配置及删除
配置永久生效的子接口,2个IP 都可以登录你这一台服务器。重启不失效。 永久的 [应用] vi /etc/sysconfig/network-scripts/ifcfg-eth0修改文件内内容 TYPE"Ethernet" BOOTPROTO"none" NAME"eth0" DEVICE"eth0" ONBOOT&q…...

docker 部署发现spring.profiles.active 问题
报错: org.springframework.boot.context.config.InvalidConfigDataPropertyException: Property spring.profiles.active imported from location class path resource [application-test.yml] is invalid in a profile specific resource [origin: class path re…...
