HDU - 4734 -- F(x)
题目如下:
For a decimal number x with n digits (AnAn−1An−2...A2A1)(A_nA_{n-1}A_{n-2} ... A_2A_1)(AnAn−1An−2...A2A1), we define its weight as F(x)=An∗2n−1+An−1∗2n−2+...+A2∗2+A1∗1.F(x) = A_n * 2^{n-1} + A_{n-1} * 2^{n-2} + ... + A_2 * 2 + A_1 * 1.F(x)=An∗2n−1+An−1∗2n−2+...+A2∗2+A1∗1. Now you are given two numbers AAA and BBB, please calculate how many numbers are there between 000 and BBB, inclusive, whose weight is no more than F(A)F(A)F(A).
Input
The first line has a number T(T≤10000)T (T \le 10000)T(T≤10000) , indicating the number of test cases.
For each test case, there are two numbers AAA and BBB (0≤A,B<109)(0 \le A,B < 10^9)(0≤A,B<109)
Output
For every case,you should output "Case #t: " at first, without quotes. The t is the case number starting from 111. Then output the answer.
Sample
Input
3
0 100
1 10
5 100
Output
Case #1: 1
Case #2: 2
Case #3: 13
思路 or 题解:
数位DP
dfs(数位, F(x) - 该位数的贡献,是否有限制)
具体请参考下面代码
AC 代码如下:
/*
Make it simple and keep self stupid
author:Joanh_Lan
*/
#pragma GCC optimize(3)
#pragma GCC optimize("inline") // 如果比赛允许开编译器优化的话,可以默写这两段
#include <iostream>
#include <algorithm>
#include <vector>
#include <string>
#include <numeric>
#include <cstring>
#include <cmath>
#include <map>
#include <unordered_map>
#include <bitset>
#include <set>
#include <random>
#include <ctime>
#include <queue>
#include <stack>
#include <climits>
#define buff \ios::sync_with_stdio(false); \cin.tie(0);
// #define int long long
#define ll long long
#define PII pair<int, int>
#define px first
#define py second
typedef std::mt19937 Random_mt19937;
Random_mt19937 rnd(time(0));
using namespace std;
const int mod = 1e9 + 7;
const int inf = 2147483647;
const int N = 100009;
//int Mod(int a,int mod){return (a%mod+mod)%mod;}
//int lowbit(int x){return x&-x;}//最低位1及其后面的0构成的数值
//int qmi(int a, int k, int p){int res = 1 % p;while (k){if (k & 1) res = Mod(res * a , p);a = Mod(a * a , p);k >>= 1;}return res;}
//int inv(int a,int mod){return qmi(a,mod-2,mod);}
//int lcm(int a,int b){return a*b/__gcd(a,b);}
int f[30][N], dig[30], idx;
int calc(int x)
{int ans = 0, t = 1;while (x)ans += x % 10 * t, t <<= 1, x /= 10;return ans;
}
int dfs(int pos, int s, bool lim)
{if (pos == -1) return s >= 0;if (s < 0)return 0;if (!lim && f[pos][s] != -1) return f[pos][s];int len = lim ? dig[pos] : 9;int ans = 0;for (int i = 0; i <= len; i++)ans += dfs(pos - 1, s - i * (1 << pos), lim && i == len);if (!lim) f[pos][s] = ans;return ans;
}
void solve()
{int x, n; cin >> x >> n;idx = 0;while (n)dig[idx++] = n % 10, n /= 10;cout << dfs(idx - 1, calc(x), 1) << '\n';
}
int main()
{buff;memset(f, -1, sizeof f);int _ = 1;cin >> _;for (int i = 1; i <= _; i++){cout << "Case #" << i << ": ";solve();}
}
相关文章:
)
HDU - 4734 -- F(x)
题目如下: For a decimal number x with n digits (AnAn−1An−2...A2A1)(A_nA_{n-1}A_{n-2} ... A_2A_1)(AnAn−1An−2...A2A1), we define its weight as F(x)An∗2n−1An−1∗2n−2...A2∗2A1∗1.F(x) A_n * 2^{n-1} A_{n-1} * 2^{n-2} ... A_2 *…...
)
【音视频第10天】GCC论文阅读(1)
A Google Congestion Control Algorithm for Real-Time Communication draft-alvestrand-rmcat-congestion-03论文理解 看中文的GCC算法一脸懵。看一看英文版的,找一找感觉。 目录Abstract1. Introduction1.1 Mathematical notation conventions2. System model3.Fe…...

如何进行移动设备资产管理
随着越来越多的移动设备进入和访问组织的企业资源,管理员必须监视和控制对企业数据的访问。与传统工作站不同,传统工作站位于企业的物理工作区内,移动设备从多个位置使用,从而使移动资产管理过程更加复杂。 什么是移动资产管理 …...
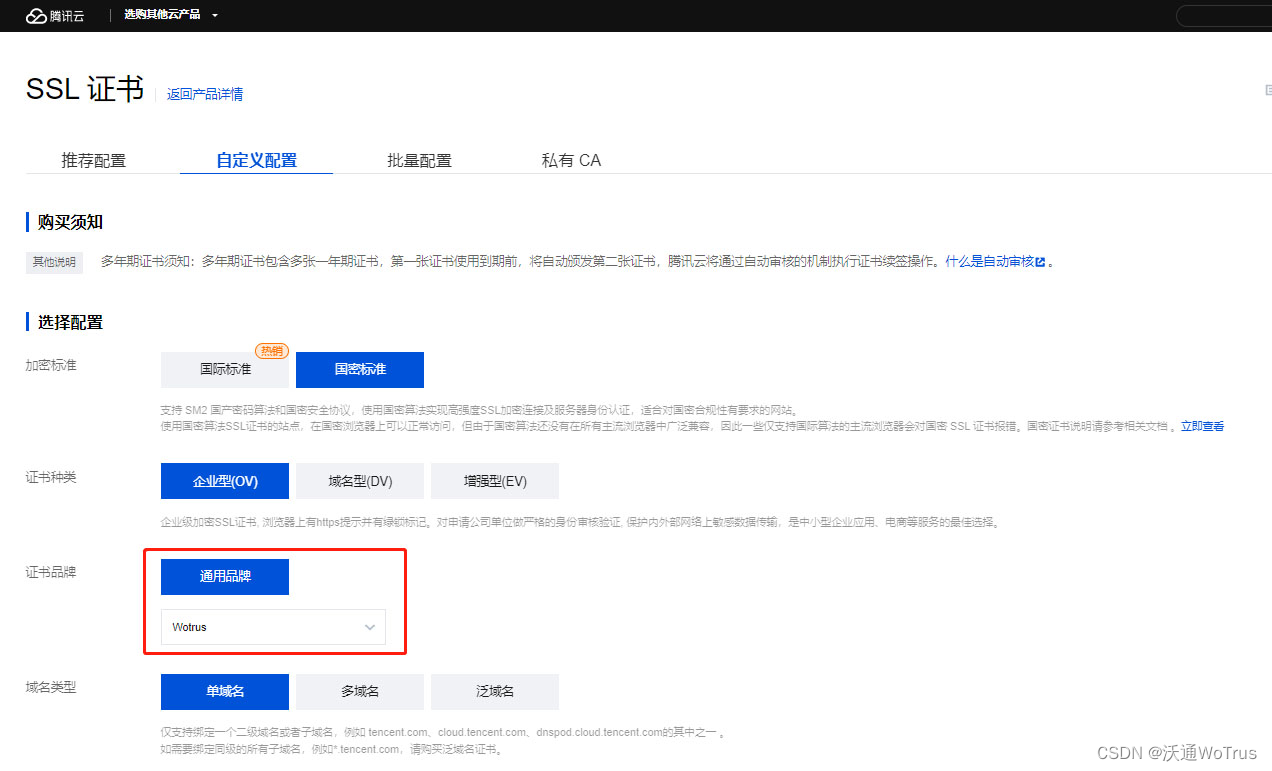
使用国密SSL证书,实现SSL/TLS传输层国密改造
密码是保障网络空间安全可信的核心技术和基础支撑,通过自主可控的国产密码技术保护重要数据的安全,是有效提升我国信息安全保障水平的重要举措。因此,我国高度重视商用密码算法的应用并出台相关政策法规,大力推动国产商用密码算法…...
)
Oracle之增删改(六)
1、插入语句 insert into 表名(列名1,列名2,…) values(值,值,…) insert into 关键字 列名(要插入数据的列),可以省略,省略时表示给表中的每个字段都插入数据 value 赋值关键字 使用这种语法一…...

OJ练习第81题——岛屿数量
岛屿数量 力扣链接:200. 岛屿数量 题目描述 给你一个由 ‘1’(陆地)和 ‘0’(水)组成的的二维网格,请你计算网格中岛屿的数量。 岛屿总是被水包围,并且每座岛屿只能由水平方向和/或竖直方向…...

remote gdb 操作流程
进行gdb调试时,tui可以方便地显示源代码、汇编和寄存器文本窗口。在进入gdb界面后,使用TUI快捷键(ctrlXA)可以打开/关闭tui。 出现"找不到源码"的提示时,可以通过dir加源码路径来设置源码查找路径ÿ…...
STM32基础代码学习G070CB串口透传调试(出厂默认)代码
先下载 一定记得回车换行勾选 可以参考“Quectel_BC260Y-CN_AT命令手册_V1.0.pdf” ATCGMI 查询制造商信息 ATCGMM 查询模块型号 ATCSQ 上报信号质量 ATCGATT? PS 域附着或去附着查看板子是否正常 再激活 ATQIACT1,最后查询ATQIACT? 配置阿里云mqtt atqmtc…...
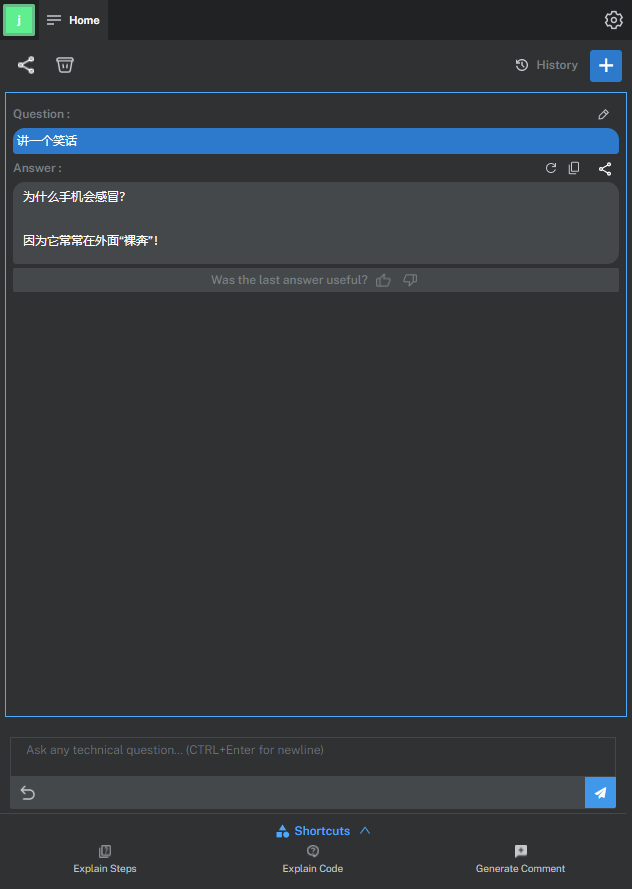
介绍一款idea神级插件【Bito-ChatGPT】
什么是Bito? Bito是一款在IntelliJ IDEA编辑器中的插件,Bito插件是由ChatGPT团队开发的,它是ChatGPT团队为了提高开发效率而开发的一款工具。ChatGPT团队是一支专注于自然语言处理技术的团队,他们开发了一款基于GPT的自然语言处理…...

pycharm 2021.2.2 版本之前试用期过了怎么办
pycharm 2021.2.2 版本之前试用期过了怎么办 虽然 jetbrains 的产品是商业收费,而且价格不菲,但官方还是为免费使用留下的空间,实在良心。 收费版可以免费试用30天,问题是30天试用期过后,怎么办,可以再次试…...

【通世智库】宁晓红:医疗更完整的样子
2022年的10月,北京协和医院缓和医学中心成立了,这是巨大的好消息!北京协和医院连续13年蝉联中国医院排行榜榜首,它率先成立了缓和医学中心,可见缓和医疗在医学领域的重要地位和不可估量的价值。【作者:宁晓…...
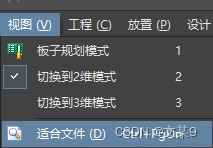
AD20打开PCB后找不到
如出现下图情况 方法1 长按ctrl且滚轮下滑 方法2 依次点击视图 适合文件...

RTC 基础
简单的一个框架 一、上行 1.音频 音频采集->3A处理->混合(麦克风bgm自定义音频)->编码->fec->打网络包(UDT/QUIC/SRT)->加密->socket发送 2.视频 视频采集->编码->切片->fec->打网络包(UDT/QUIC/SRC)->加密->socket发送 二、下行…...

Quaternion插值方法
介绍 unity,四元数Quaternion插值方法介绍 方法 线性插值(Lerp): 适用范围:适用于需要简单平滑地过渡的情况,比如物体的位置、大小等。 优点:计算简单,效率高。 缺点:不…...

如何配置Stash以便与4EVERLAND一起使用
What is Stash? AppsCode的Stash是一个可靠的工具,用于备份和恢复Kubernetes卷和应用程序。有了Stash,你可以通过定期备份和在数据丢失或系统故障时恢复这些数据来轻松保护你的宝贵数据。Stash功能多样,可用于备份各种Kubernetes资源的数据…...

webpack plugin源码解析(四) HashedModuleIdsPlugin
文章目录作用涉及 webpack API获取chunkGraph获取当前编译过程中被使用过的 module id:compilation.usedModuleIds获取当前编译过程中所有的模块对象:compilation.modules判断 module 是否需要生成 id:module.needId获取指定module 的 module…...

pytorch | 使用vmap对自定义函数进行并行化/ 向量化的执行
0. 参考 pytorch官方文档:https://pytorch.org/docs/stable/generated/torch.func.vmap.html#torch-func-vmap关于if语句如何执行:https://github.com/pytorch/functorch/issues/257 1. 问题背景 笔者现在需要执行如下的功能: root_ls [fu…...
Docker部署RabbitMQ(单机,集群,仲裁队列)
RabbitMQ部署指南 1.单机部署 我们在Centos7虚拟机中使用Docker来安装。 1.1.下载镜像 方式一:在线拉取 docker pull rabbitmq:3-management方式二:从本地加载 在课前资料已经提供了镜像包: 上传到虚拟机中后,使用命令加载镜…...

生活污水处理设备选购指南
生活污水中含有大量的有机物(如蛋白质、碳水化合物、脂肪、尿素、氨氮等)及大量的病原微生物,可导致传染病蔓延流行。因此,生活污水在排放前,需要进行处理。那么如何正确的选择生活污水处理设备呢? 一、生活…...

奥威BI数据可视化大屏分享|多场景、多风格
数据可视化大屏一般应用在品牌推广展示、商务交流、数据分析决策、数据监控等场景,由此催生出各种不同风格的BI数据可视化大屏设计。下面就从奥威BI软件的BI报表模板中截取几个有着不同风格,起着不同作用的BI数据可视化大屏报表,一起来了解一…...

KubeSphere 容器平台高可用:环境搭建与可视化操作指南
Linux_k8s篇 欢迎来到Linux的世界,看笔记好好学多敲多打,每个人都是大神! 题目:KubeSphere 容器平台高可用:环境搭建与可视化操作指南 版本号: 1.0,0 作者: 老王要学习 日期: 2025.06.05 适用环境: Ubuntu22 文档说…...

【Python】 -- 趣味代码 - 小恐龙游戏
文章目录 文章目录 00 小恐龙游戏程序设计框架代码结构和功能游戏流程总结01 小恐龙游戏程序设计02 百度网盘地址00 小恐龙游戏程序设计框架 这段代码是一个基于 Pygame 的简易跑酷游戏的完整实现,玩家控制一个角色(龙)躲避障碍物(仙人掌和乌鸦)。以下是代码的详细介绍:…...

golang循环变量捕获问题
在 Go 语言中,当在循环中启动协程(goroutine)时,如果在协程闭包中直接引用循环变量,可能会遇到一个常见的陷阱 - 循环变量捕获问题。让我详细解释一下: 问题背景 看这个代码片段: fo…...

大型活动交通拥堵治理的视觉算法应用
大型活动下智慧交通的视觉分析应用 一、背景与挑战 大型活动(如演唱会、马拉松赛事、高考中考等)期间,城市交通面临瞬时人流车流激增、传统摄像头模糊、交通拥堵识别滞后等问题。以演唱会为例,暖城商圈曾因观众集中离场导致周边…...

基于Flask实现的医疗保险欺诈识别监测模型
基于Flask实现的医疗保险欺诈识别监测模型 项目截图 项目简介 社会医疗保险是国家通过立法形式强制实施,由雇主和个人按一定比例缴纳保险费,建立社会医疗保险基金,支付雇员医疗费用的一种医疗保险制度, 它是促进社会文明和进步的…...

FastAPI 教程:从入门到实践
FastAPI 是一个现代、快速(高性能)的 Web 框架,用于构建 API,支持 Python 3.6。它基于标准 Python 类型提示,易于学习且功能强大。以下是一个完整的 FastAPI 入门教程,涵盖从环境搭建到创建并运行一个简单的…...

08. C#入门系列【类的基本概念】:开启编程世界的奇妙冒险
C#入门系列【类的基本概念】:开启编程世界的奇妙冒险 嘿,各位编程小白探险家!欢迎来到 C# 的奇幻大陆!今天咱们要深入探索这片大陆上至关重要的 “建筑”—— 类!别害怕,跟着我,保准让你轻松搞…...

Windows安装Miniconda
一、下载 https://www.anaconda.com/download/success 二、安装 三、配置镜像源 Anaconda/Miniconda pip 配置清华镜像源_anaconda配置清华源-CSDN博客 四、常用操作命令 Anaconda/Miniconda 基本操作命令_miniconda创建环境命令-CSDN博客...

Golang——6、指针和结构体
指针和结构体 1、指针1.1、指针地址和指针类型1.2、指针取值1.3、new和make 2、结构体2.1、type关键字的使用2.2、结构体的定义和初始化2.3、结构体方法和接收者2.4、给任意类型添加方法2.5、结构体的匿名字段2.6、嵌套结构体2.7、嵌套匿名结构体2.8、结构体的继承 3、结构体与…...

redis和redission的区别
Redis 和 Redisson 是两个密切相关但又本质不同的技术,它们扮演着完全不同的角色: Redis: 内存数据库/数据结构存储 本质: 它是一个开源的、高性能的、基于内存的 键值存储数据库。它也可以将数据持久化到磁盘。 核心功能: 提供丰…...
