OJ练习第70题——困于环中的机器人
困于环中的机器人
力扣链接:1041. 困于环中的机器人
题目描述
在无限的平面上,机器人最初位于 (0, 0) 处,面朝北方。注意:
北方向 是y轴的正方向。
南方向 是y轴的负方向。
东方向 是x轴的正方向。
西方向 是x轴的负方向。
机器人可以接受下列三条指令之一:
“G”:直走 1 个单位
“L”:左转 90 度
“R”:右转 90 度
机器人按顺序执行指令 instructions,并一直重复它们。
只有在平面中存在环使得机器人永远无法离开时,返回 true。否则,返回 false。
示例
示例 1:
输入:instructions = “GGLLGG”
输出:true
解释:机器人最初在(0,0)处,面向北方。
“G”:移动一步。位置:(0,1)方向:北。
“G”:移动一步。位置:(0,2).方向:北。
“L”:逆时针旋转90度。位置:(0,2).方向:西。
“L”:逆时针旋转90度。位置:(0,2)方向:南。
“G”:移动一步。位置:(0,1)方向:南。
“G”:移动一步。位置:(0,0)方向:南。
重复指令,机器人进入循环:(0,0)——>(0,1)——>(0,2)——>(0,1)——>(0,0)。
在此基础上,我们返回true。
示例 2:
输入:instructions = “GG”
输出:false
解释:机器人最初在(0,0)处,面向北方。
“G”:移动一步。位置:(0,1)方向:北。
“G”:移动一步。位置:(0,2).方向:北。
重复这些指示,继续朝北前进,不会进入循环。
在此基础上,返回false。
思路
由于已知重复顺序执行指令,所以如果机器人能够回到原点的的话,只会存在三种情况:1、顺序执行一次就回到原点。2、顺序执行两次回到原点。3、顺序执行四次回到原点。否则,机器人将永远不能回到原点。所以就同意都按照四次来。
代码
class Solution {public boolean isRobotBounded(String instructions) {int x = 0, y = 0, d = 0;int[][] direcions = {{0,1}, {-1,0},{0,-1}, {1,0}};int n = 4;while(n-- > 0) {for(char ch : instructions.toCharArray()) {if(ch == 'G') {x += direcions[d][0];y += direcions[d][1];}else if(ch == 'L') {d = (d + 1) % 4;}else {d = (d + 3) % 4;}}}if(x == 0 && y == 0 && d == 0) {return true;}return false;}
}
来源:力扣(LeetCode)
链接:https://leetcode.cn/problems/robot-bounded-in-circle
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
相关文章:

OJ练习第70题——困于环中的机器人
困于环中的机器人 力扣链接:1041. 困于环中的机器人 题目描述 在无限的平面上,机器人最初位于 (0, 0) 处,面朝北方。注意: 北方向 是y轴的正方向。 南方向 是y轴的负方向。 东方向 是x轴的正方向。 西方向 是x轴的负方向。 机器人可以接受…...

运行时内存数据区之虚拟机栈——局部变量表
这篇内容十分重要,文字也很多,仔细阅读后,你必定有所收获! 基本内容 与程序计数器一样,Java虚拟机栈(Java Virtual Machine Stack)也是线程私有的,它的生命周期与线程相同。虚拟机栈描述的是Java方法执行的线程内存模型…...
Java中常用算法及示例-分治、迭代、递归、递推、动态规划、回溯、穷举、贪心
场景 1、分治算法的基本思想是将一个计算复杂的问题分成规模较小、计算简单的小问题求解, 然后综合各个小问题,得到最终答案。 2、穷举(又称枚举)算法的基本思想是从所有可能的情况中搜索正确的答案。 3、迭代法(Iterative Method) 无法使用公式一次…...

2个 windows 下的网络测试工具
环境windows 10 64bittcpingtcproute简介TCPing 和 TCProute 都是 windows 下的用于测试 TCP 连接的工具,它们可以帮助用户确定网络连接的可用性和响应时间。TCPing下载地址: https://elifulkerson.com/projects/tcping.phpTCPing 通过向目标主机发送 TC…...
)
HDU - 4734 -- F(x)
题目如下: For a decimal number x with n digits (AnAn−1An−2...A2A1)(A_nA_{n-1}A_{n-2} ... A_2A_1)(AnAn−1An−2...A2A1), we define its weight as F(x)An∗2n−1An−1∗2n−2...A2∗2A1∗1.F(x) A_n * 2^{n-1} A_{n-1} * 2^{n-2} ... A_2 *…...
)
【音视频第10天】GCC论文阅读(1)
A Google Congestion Control Algorithm for Real-Time Communication draft-alvestrand-rmcat-congestion-03论文理解 看中文的GCC算法一脸懵。看一看英文版的,找一找感觉。 目录Abstract1. Introduction1.1 Mathematical notation conventions2. System model3.Fe…...

如何进行移动设备资产管理
随着越来越多的移动设备进入和访问组织的企业资源,管理员必须监视和控制对企业数据的访问。与传统工作站不同,传统工作站位于企业的物理工作区内,移动设备从多个位置使用,从而使移动资产管理过程更加复杂。 什么是移动资产管理 …...
使用国密SSL证书,实现SSL/TLS传输层国密改造
密码是保障网络空间安全可信的核心技术和基础支撑,通过自主可控的国产密码技术保护重要数据的安全,是有效提升我国信息安全保障水平的重要举措。因此,我国高度重视商用密码算法的应用并出台相关政策法规,大力推动国产商用密码算法…...
)
Oracle之增删改(六)
1、插入语句 insert into 表名(列名1,列名2,…) values(值,值,…) insert into 关键字 列名(要插入数据的列),可以省略,省略时表示给表中的每个字段都插入数据 value 赋值关键字 使用这种语法一…...

OJ练习第81题——岛屿数量
岛屿数量 力扣链接:200. 岛屿数量 题目描述 给你一个由 ‘1’(陆地)和 ‘0’(水)组成的的二维网格,请你计算网格中岛屿的数量。 岛屿总是被水包围,并且每座岛屿只能由水平方向和/或竖直方向…...

remote gdb 操作流程
进行gdb调试时,tui可以方便地显示源代码、汇编和寄存器文本窗口。在进入gdb界面后,使用TUI快捷键(ctrlXA)可以打开/关闭tui。 出现"找不到源码"的提示时,可以通过dir加源码路径来设置源码查找路径ÿ…...
STM32基础代码学习G070CB串口透传调试(出厂默认)代码
先下载 一定记得回车换行勾选 可以参考“Quectel_BC260Y-CN_AT命令手册_V1.0.pdf” ATCGMI 查询制造商信息 ATCGMM 查询模块型号 ATCSQ 上报信号质量 ATCGATT? PS 域附着或去附着查看板子是否正常 再激活 ATQIACT1,最后查询ATQIACT? 配置阿里云mqtt atqmtc…...
介绍一款idea神级插件【Bito-ChatGPT】
什么是Bito? Bito是一款在IntelliJ IDEA编辑器中的插件,Bito插件是由ChatGPT团队开发的,它是ChatGPT团队为了提高开发效率而开发的一款工具。ChatGPT团队是一支专注于自然语言处理技术的团队,他们开发了一款基于GPT的自然语言处理…...

pycharm 2021.2.2 版本之前试用期过了怎么办
pycharm 2021.2.2 版本之前试用期过了怎么办 虽然 jetbrains 的产品是商业收费,而且价格不菲,但官方还是为免费使用留下的空间,实在良心。 收费版可以免费试用30天,问题是30天试用期过后,怎么办,可以再次试…...

【通世智库】宁晓红:医疗更完整的样子
2022年的10月,北京协和医院缓和医学中心成立了,这是巨大的好消息!北京协和医院连续13年蝉联中国医院排行榜榜首,它率先成立了缓和医学中心,可见缓和医疗在医学领域的重要地位和不可估量的价值。【作者:宁晓…...
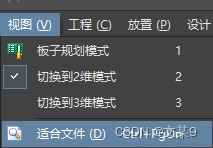
AD20打开PCB后找不到
如出现下图情况 方法1 长按ctrl且滚轮下滑 方法2 依次点击视图 适合文件...

RTC 基础
简单的一个框架 一、上行 1.音频 音频采集->3A处理->混合(麦克风bgm自定义音频)->编码->fec->打网络包(UDT/QUIC/SRT)->加密->socket发送 2.视频 视频采集->编码->切片->fec->打网络包(UDT/QUIC/SRC)->加密->socket发送 二、下行…...

Quaternion插值方法
介绍 unity,四元数Quaternion插值方法介绍 方法 线性插值(Lerp): 适用范围:适用于需要简单平滑地过渡的情况,比如物体的位置、大小等。 优点:计算简单,效率高。 缺点:不…...

如何配置Stash以便与4EVERLAND一起使用
What is Stash? AppsCode的Stash是一个可靠的工具,用于备份和恢复Kubernetes卷和应用程序。有了Stash,你可以通过定期备份和在数据丢失或系统故障时恢复这些数据来轻松保护你的宝贵数据。Stash功能多样,可用于备份各种Kubernetes资源的数据…...

webpack plugin源码解析(四) HashedModuleIdsPlugin
文章目录作用涉及 webpack API获取chunkGraph获取当前编译过程中被使用过的 module id:compilation.usedModuleIds获取当前编译过程中所有的模块对象:compilation.modules判断 module 是否需要生成 id:module.needId获取指定module 的 module…...

K8S认证|CKS题库+答案| 11. AppArmor
目录 11. AppArmor 免费获取并激活 CKA_v1.31_模拟系统 题目 开始操作: 1)、切换集群 2)、切换节点 3)、切换到 apparmor 的目录 4)、执行 apparmor 策略模块 5)、修改 pod 文件 6)、…...

【入坑系列】TiDB 强制索引在不同库下不生效问题
文章目录 背景SQL 优化情况线上SQL运行情况分析怀疑1:执行计划绑定问题?尝试:SHOW WARNINGS 查看警告探索 TiDB 的 USE_INDEX 写法Hint 不生效问题排查解决参考背景 项目中使用 TiDB 数据库,并对 SQL 进行优化了,添加了强制索引。 UAT 环境已经生效,但 PROD 环境强制索…...

从零开始打造 OpenSTLinux 6.6 Yocto 系统(基于STM32CubeMX)(九)
设备树移植 和uboot设备树修改的内容同步到kernel将设备树stm32mp157d-stm32mp157daa1-mx.dts复制到内核源码目录下 源码修改及编译 修改arch/arm/boot/dts/st/Makefile,新增设备树编译 stm32mp157f-ev1-m4-examples.dtb \stm32mp157d-stm32mp157daa1-mx.dtb修改…...

JAVA后端开发——多租户
数据隔离是多租户系统中的核心概念,确保一个租户(在这个系统中可能是一个公司或一个独立的客户)的数据对其他租户是不可见的。在 RuoYi 框架(您当前项目所使用的基础框架)中,这通常是通过在数据表中增加一个…...

LeetCode - 199. 二叉树的右视图
题目 199. 二叉树的右视图 - 力扣(LeetCode) 思路 右视图是指从树的右侧看,对于每一层,只能看到该层最右边的节点。实现思路是: 使用深度优先搜索(DFS)按照"根-右-左"的顺序遍历树记录每个节点的深度对于…...

网站指纹识别
网站指纹识别 网站的最基本组成:服务器(操作系统)、中间件(web容器)、脚本语言、数据厍 为什么要了解这些?举个例子:发现了一个文件读取漏洞,我们需要读/etc/passwd,如…...
提供了哪些便利?)
现有的 Redis 分布式锁库(如 Redisson)提供了哪些便利?
现有的 Redis 分布式锁库(如 Redisson)相比于开发者自己基于 Redis 命令(如 SETNX, EXPIRE, DEL)手动实现分布式锁,提供了巨大的便利性和健壮性。主要体现在以下几个方面: 原子性保证 (Atomicity)ÿ…...

基于Springboot+Vue的办公管理系统
角色: 管理员、员工 技术: 后端: SpringBoot, Vue2, MySQL, Mybatis-Plus 前端: Vue2, Element-UI, Axios, Echarts, Vue-Router 核心功能: 该办公管理系统是一个综合性的企业内部管理平台,旨在提升企业运营效率和员工管理水…...

Golang——6、指针和结构体
指针和结构体 1、指针1.1、指针地址和指针类型1.2、指针取值1.3、new和make 2、结构体2.1、type关键字的使用2.2、结构体的定义和初始化2.3、结构体方法和接收者2.4、给任意类型添加方法2.5、结构体的匿名字段2.6、嵌套结构体2.7、嵌套匿名结构体2.8、结构体的继承 3、结构体与…...

解析奥地利 XARION激光超声检测系统:无膜光学麦克风 + 无耦合剂的技术协同优势及多元应用
在工业制造领域,无损检测(NDT)的精度与效率直接影响产品质量与生产安全。奥地利 XARION开发的激光超声精密检测系统,以非接触式光学麦克风技术为核心,打破传统检测瓶颈,为半导体、航空航天、汽车制造等行业提供了高灵敏…...
