【id:45】【20分】A. Equation(类与对象+构造)
题目描述
建立一个类Equation,表达方程ax2+bx+c=0。类中至少包含以下方法:
1、无参构造(abc默认值为1.0、1.0、0)与有参构造函数,用于初始化a、b、c的值;
2、set方法,用于修改a、b、c的值
3、getRoot方法,求出方程的根。
一元二次方程的求根公式如下:
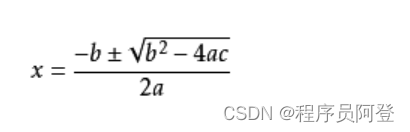
一元二次方程的求解分三种情况,如下:

输入
输入测试数据的组数t
第一组a、b、c
第二组a、b、c
输出
输出方程的根,结果到小数点后2位
在C++中,输出指定精度的参考代码如下:
#include <iostream>
#include <iomanip> //必须包含这个头文件
using namespace std;
void main( )
{ double a =3.14;
cout<<fixed<<setprecision(3)<<a<<endl; //输出小数点后3位
}
输入样例
3
2 4 2
2 2 2
2 8 2
输出样例
x1=x2=-1.00
x1=-0.50+0.87i x2=-0.50-0.87i
x1=-0.27 x2=-3.73

#include <iostream>
#include <iomanip> //必须包含这个头文件
#include <math.h>
using namespace std;class Eq
{
private:double a, b, c, x1, x2;
public:Eq() { a = 1; b = 1; c = 0; x1 = x2 = 0; };//初始void set(double x, double y, double z);//赋值void getRoot();//求根
};//赋值
void Eq::set(double x, double y, double z)
{a = x; b = y; c = z;//cout << a << b << c <<" 1" << endl;
}//Δ=b^2-4ac≥0时,x=[-b±(b^2-4ac)^(1/2)]/2a。当Δ=b^2-4ac<0时,x={-b±[(4ac-b^2)^(1/2)]i}/2a。
//求根
void Eq::getRoot() {double derta;derta = b * b - 4 * a * c;if (derta > 0){x1 = ((-b) + sqrt(derta)) / (2 * a);x2 = ((-b) - sqrt(derta)) / (2 * a);cout << "x1=" << fixed << setprecision(2) << x1<< " x2=" << fixed << setprecision(2) << x2 << endl;}if (derta == 0){x1 = ((-b) + sqrt(derta)) / (2 * a);cout << "x1=x2=" << fixed << setprecision(2) << x1 << endl;}if (derta < 0){double i1;x1 = (-b) / (2 * a);i1 = sqrt(-derta) / (2 * a);cout << "x1=" << fixed << setprecision(2) << x1 << "+" << fixed << setprecision(2) << i1 << "i "<< "x2=" << fixed << setprecision(2) << x1 << "-" << fixed << setprecision(2) << i1 << 'i' << endl;}
}int main()
{int t;cin >> t;for (int i = 0; i < t; i++){Eq* a = new Eq[t];//动态数组double x, y, z;cin >> x >> y >> z;a[i].set(x, y, z);//传入数字进去a[i].getRoot();}
}相关文章:

【id:45】【20分】A. Equation(类与对象+构造)
题目描述 建立一个类Equation,表达方程ax2bxc0。类中至少包含以下方法: 1、无参构造(abc默认值为1.0、1.0、0)与有参构造函数,用于初始化a、b、c的值; 2、set方法,用于修改a、b、c的值 3、ge…...

数据库事务
什么是事务 在数据库中,事务(Transaction)是指一组数据库操作,这些操作要么全部成功执行,要么全部失败回滚,是保证数据库操作一致性的基本单位。事务具有原子性(Atomicity)、一致性…...
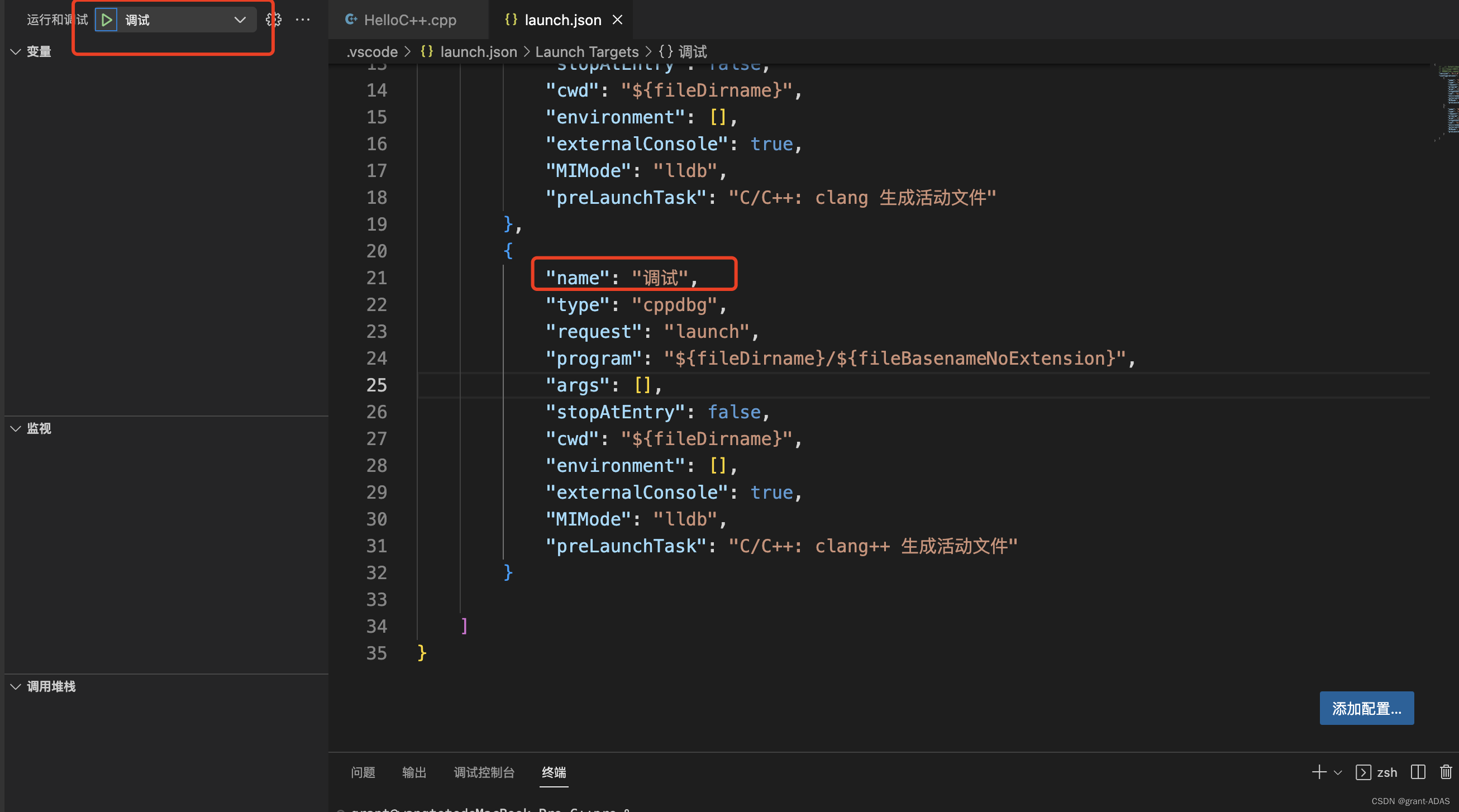
Macbook(苹果电脑) VSCode 创建简单c++程序 配置C++开发环境
1.打开 Terminal 终端(Command空格,输入Terminal)。 1.1 输入如下指令,查看是否显示版本信息。 clang --version 1.2 如果出现版本信息,则跳过,否则输入 xcode-select --install 2. 为 VS Code 安装插件 …...

如何使用 Matlab 构建深度学习模型
深度学习已经成为了AI领域的热门话题,相信很多人都想学习如何构建深度学习模型,那么,我们就一起来看看如何使用Matlab构建深度学习模型。 首先,我们需要准备好Matlab的环境。Matlab是一款非常强大的数学计算软件,它提…...
PDF怎么转CAD文件?(免费!高效转换方法汇总)
一般而言,PDF图纸是不能修改的。若需修改,则需将PDF转CAD,此时如何满足PDF转CAD的需求呢?今天,我将教你两种免费的PDF转CAD的方法,助力高效办公。 1.本地软件转换法 这是用本地软件转换方法,支…...

经历了野蛮生长之后,新科技或许已经抵达了全新的临界点
跳出仅仅只是以概念和营销的方式来定义元宇宙,真正找到元宇宙与现实商业之间的桥接,让元宇宙可以在真实实践上得到复现,才是保证元宇宙的发展可以进入到一个全新发展阶段的关键所在。归根到底,我们还是要找到元宇宙落地的正确的方…...

Segment Anything论文翻译,SAM模型,SAM论文,SAM论文翻译;一个用于图像分割的新任务、模型和数据集;SA-1B数据集
【论文翻译】- Segment Anything / Model / SAM论文 论文链接: https://arxiv.org/pdf/2304.02643.pdfhttps://ai.facebook.com/research/publications/segment-anything/ 代码连接:https://github.com/facebookresearch/segment-anything 论文翻译&…...
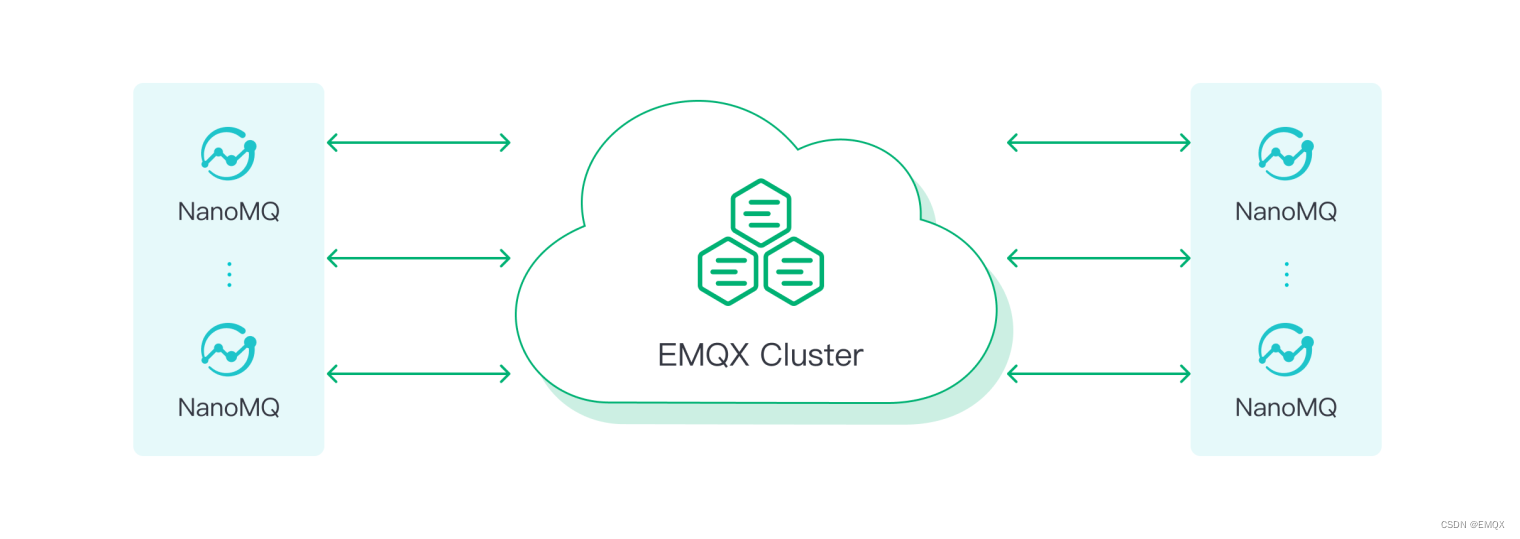
EMQX vs NanoMQ | 2023 MQTT Broker 对比
引言 EMQX 和 NanoMQ 都是由全球领先的开源物联网数据基础设施软件供应商 EMQ 开发的开源 MQTT Broker。 EMQX 是一个高度可扩展的大规模分布式 MQTT Broker,能够将百万级的物联网设备连接到云端。NanoMQ 则是专为物联网边缘场景设计的轻量级 Broker。 本文中我们…...
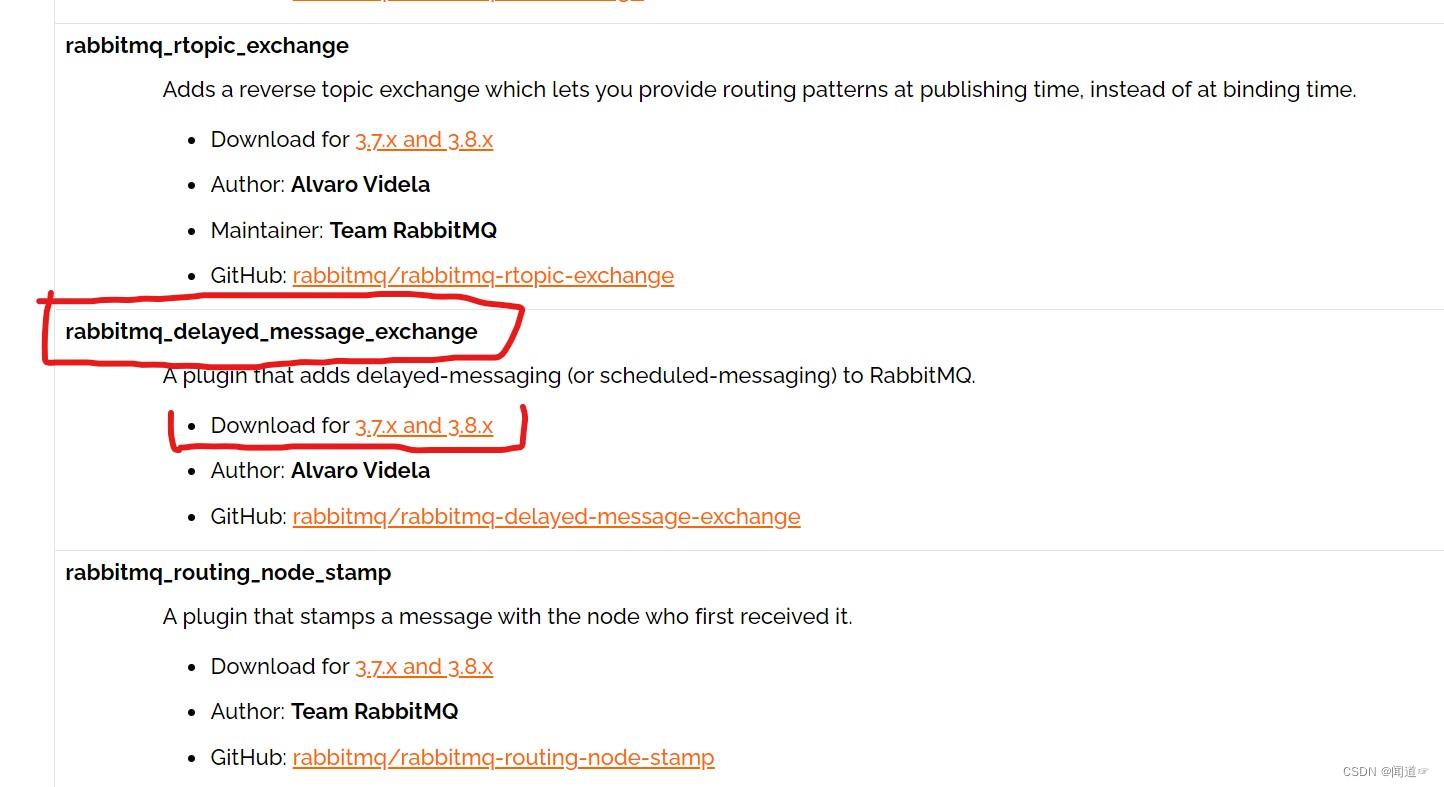
RabbitMQ实现消息的延迟推送或延迟发送
一、RabbitMQ是什么? 1.RabbitMQ简介 RabbitMQ是有erlang语言开发,基于AMQP(Advanced Message Queue 高级消息队列协议)协议实现的消息队列。 常见的消息队列有:RabbitMQ、Kafka 和 ActiveMQ 2.RabbitMQ的优点 Rab…...
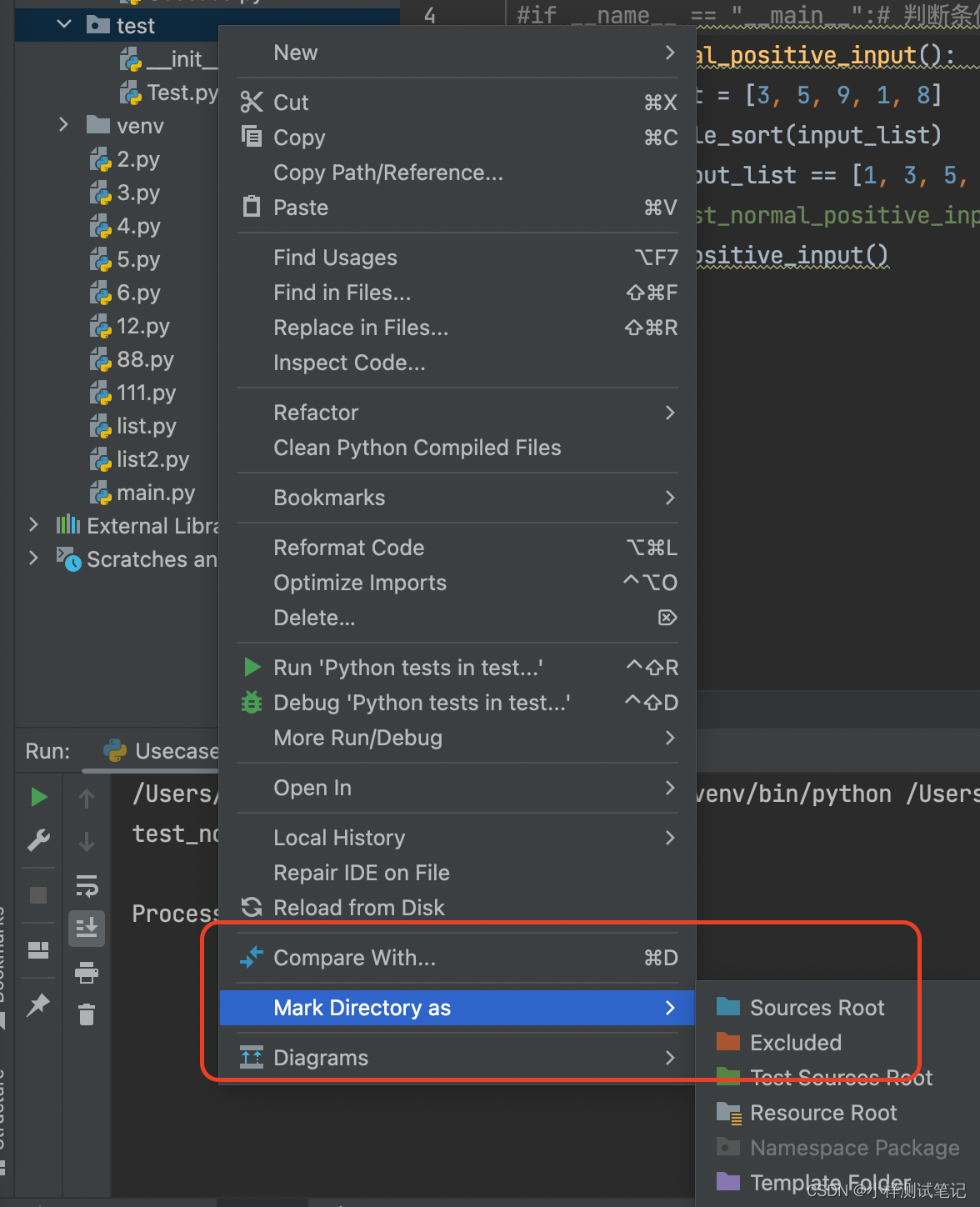
解决python中import导入自己的包呈现灰色 无效的问题
打开File–> Setting—> 打开 Console下的Python Console,把选项(Add source roots to PYTHONPAT)点击勾选上。 右键点击需要导入的工作空间文件夹,找到Mark Directory as 选择Source Root。 另外,Python中的…...

消息中间件对比
1,常见消息中间件对比(后续逐个介绍) 比较项TubeMQKafkaPulsar数据时延非常低,10ms比较低,250ms非常低,10msTPS高,14W/s一般,10W/s高,14W/s (高性能场景)过滤消费支持服务端过滤和客户端过滤客…...
nodejs+vue 高校校园食堂餐品在线订购网
食堂作为学校的一个重要的部门,为学生提供了用餐的地点,学生可以在食堂享用丰富的餐品,建立一个在校订餐网站,帮助了学生提供一个用餐订餐的系统,也帮助了食堂提供了一个餐品展示的站点。 园的食堂作为一个窗口单位&a…...
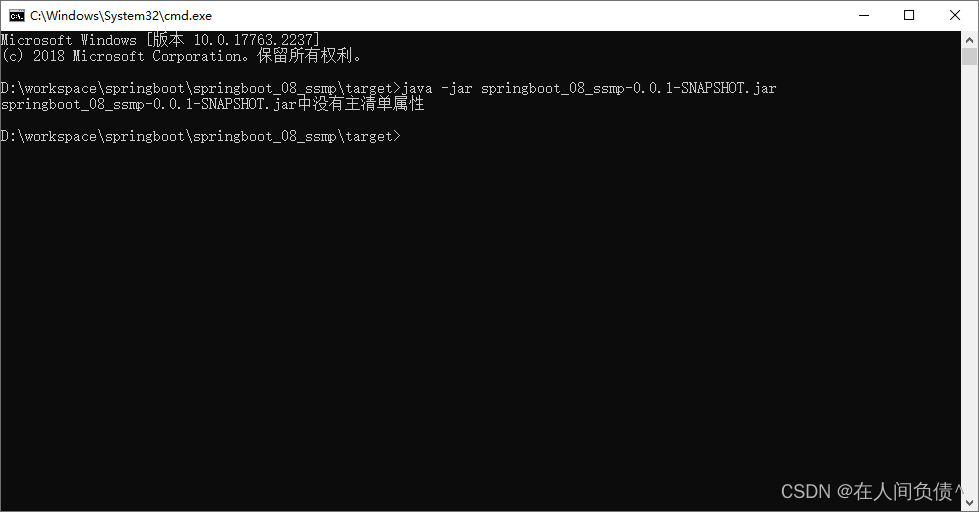
SpringBoot【运维实用篇】---- SpringBoot程序的打包与运行
SpringBoot【运维实用篇】---- SpringBoot程序的打包与运行 程序打包程序运行SpringBoot程序打包失败处理命令行启动常见问题及解决方案 刚开始做开发学习的小伙伴可能在有一个知识上面有错误的认知,我们天天写程序是在Idea下写的,运行也是在Idea下运行的…...

10万字智慧政务数据中心平台建设方案
本资料来源公开网络,仅供个人学习,请勿商用,如有侵权请联系删除。 一、 项目建设内容 1. 基础支撑平台 基础支撑平台是云教育公共服务平台各子系统的公共运行环境,提供底层数据交换、集成服务以及统一身份认证和基础数据同步服…...

使用 TensorFlow 构建机器学习项目:1~5
原文:Building Machine Learning Projects with TensorFlow 协议:CC BY-NC-SA 4.0 译者:飞龙 本文来自【ApacheCN 深度学习 译文集】,采用译后编辑(MTPE)流程来尽可能提升效率。 不要担心自己的形象&#x…...

【store商城项目08】删除用户的收获地址
1.删除收获地址-持久层 1.1规划SQL语句 根据aid判断数据是否存在,根据返回的uid判断数据是否对应(已开发)根据aid删除的SQL delete from t_address where aid ?根据1中的SQL返回的对象判断是否为默认地址,若为默认地址&#…...

SpringBooot
目录 一、简介 1、使用原因 2、JavaConfig (1)Configuration注解 (2)Bean注解 (3)ImportResource注解 (4)PropertyResource注解 (5)案例 3、简介 4…...
)
测牛学堂:2023软件测试linux和shell脚本入门系列(shell的运算符)
shell中的注释 以# 开头的就是shell中的注释,不会被执行,是给编程的人看的。 shell中的运算符 shell中有很多运算符。 按照分类,可以分为算术运算符,关系运算符,布尔运算符,字符串运算符,文件…...

TensorFlow 2.0 快速入门指南:第三部分
原文:TensorFlow 2.0 Quick Start Guide 协议:CC BY-NC-SA 4.0 译者:飞龙 本文来自【ApacheCN 深度学习 译文集】,采用译后编辑(MTPE)流程来尽可能提升效率。 不要担心自己的形象,只关心如何实现…...

webpack介绍
webpack是一个静态资源打包工具 开发时,我们会使用框架(Vue,React),ES6模块化语法,Less/Sass等css预处理器等语法进行开发。 这样的代码想要在浏览器运行必须经过编译成浏览器能识别的JS、CSS等语法&#x…...

【人工智能】神经网络的优化器optimizer(二):Adagrad自适应学习率优化器
一.自适应梯度算法Adagrad概述 Adagrad(Adaptive Gradient Algorithm)是一种自适应学习率的优化算法,由Duchi等人在2011年提出。其核心思想是针对不同参数自动调整学习率,适合处理稀疏数据和不同参数梯度差异较大的场景。Adagrad通…...

LeetCode - 394. 字符串解码
题目 394. 字符串解码 - 力扣(LeetCode) 思路 使用两个栈:一个存储重复次数,一个存储字符串 遍历输入字符串: 数字处理:遇到数字时,累积计算重复次数左括号处理:保存当前状态&a…...

WordPress插件:AI多语言写作与智能配图、免费AI模型、SEO文章生成
厌倦手动写WordPress文章?AI自动生成,效率提升10倍! 支持多语言、自动配图、定时发布,让内容创作更轻松! AI内容生成 → 不想每天写文章?AI一键生成高质量内容!多语言支持 → 跨境电商必备&am…...
的原因分类及对应排查方案)
JVM暂停(Stop-The-World,STW)的原因分类及对应排查方案
JVM暂停(Stop-The-World,STW)的完整原因分类及对应排查方案,结合JVM运行机制和常见故障场景整理而成: 一、GC相关暂停 1. 安全点(Safepoint)阻塞 现象:JVM暂停但无GC日志,日志显示No GCs detected。原因:JVM等待所有线程进入安全点(如…...

GC1808高性能24位立体声音频ADC芯片解析
1. 芯片概述 GC1808是一款24位立体声音频模数转换器(ADC),支持8kHz~96kHz采样率,集成Δ-Σ调制器、数字抗混叠滤波器和高通滤波器,适用于高保真音频采集场景。 2. 核心特性 高精度:24位分辨率,…...

CSS设置元素的宽度根据其内容自动调整
width: fit-content 是 CSS 中的一个属性值,用于设置元素的宽度根据其内容自动调整,确保宽度刚好容纳内容而不会超出。 效果对比 默认情况(width: auto): 块级元素(如 <div>)会占满父容器…...

【JVM】Java虚拟机(二)——垃圾回收
目录 一、如何判断对象可以回收 (一)引用计数法 (二)可达性分析算法 二、垃圾回收算法 (一)标记清除 (二)标记整理 (三)复制 (四ÿ…...

Oracle11g安装包
Oracle 11g安装包 适用于windows系统,64位 下载路径 oracle 11g 安装包...
)
stm32进入Infinite_Loop原因(因为有系统中断函数未自定义实现)
这是系统中断服务程序的默认处理汇编函数,如果我们没有定义实现某个中断函数,那么当stm32产生了该中断时,就会默认跑这里来了,所以我们打开了什么中断,一定要记得实现对应的系统中断函数,否则会进来一直循环…...
)
python数据结构和算法(1)
数据结构和算法简介 数据结构:存储和组织数据的方式,决定了数据的存储方式和访问方式。 算法:解决问题的思维、步骤和方法。 程序 数据结构 算法 算法 算法的独立性 算法是独立存在的一种解决问题的方法和思想,对于算法而言&a…...
