【学习笔记】ARC159
D - LIS 2
因为没有让你求方案数,所以还是比较好做的。
如果每一个连续段都退化成一个点,那么答案就是直接求 L I S LIS LIS。
否则,假设我们选了一些连续段把它们拼起来形成答案,显然我们有 r i + 1 ≥ l i r_{i+1}\ge l_i ri+1≥li,否则这两段不能同时存在;并且其中一段不能包含另一段,否则可以把另一段删去。那么,如果 l i + 1 > r i l_{i+1}>r_i li+1>ri,答案显然就是两段的长度加起来;如果 l i + 1 ≥ r i l_{i+1}\ge r_i li+1≥ri,那么中间那一段重复的部分不管它,答案是 r i + 1 − l i + 1 r_{i+1}-l_i+1 ri+1−li+1。
用线段树维护就做完了。复杂度 O ( n log n ) O(n\log n) O(nlogn)。
E - Difference Sum Query
非常好的谜题。但是我不会。
首先,根据 a i b i \frac{a_i}{b_i} biai的范围不难得出新的区间长度不会超过原长度的 2 3 \frac{2}{3} 32,因此 X i ≤ log N X_i\le \log N Xi≤logN。
然后,根据 { X i } \{X_i\} {Xi}的构造过程,我们可以建立一颗二叉树,那么一个点的值就是它的深度。显然 i i i和 i + 1 i+1 i+1之间是存在祖先关系的,因此问题转化为从 l l l走到 l + 1 , . . . , r l+1,...,r l+1,...,r过程中经过的路径长度。
做到这一步,感觉非常不可做。我们需要非常神奇的结论:假设让 r r r重新走回 l l l,那么答案就是 [ l , r ] [l,r] [l,r]之间的点组成的虚树的边的数目乘 2 2 2。这非常好理解,因为上述过程恰好就是做了一遍 D F S DFS DFS。今天思路实在是非常混乱,不过我们还是尝试证明一下这个结论。事实上我们只需要用到:因为是二叉搜索树,所以子树内编号是连续的,因此进入一个子树后会把会把子树内能走的点走完,出去后就再也进不来了。
那么我们只要求出虚树点的数目即可。显然只需要求 l , r l,r l,r路径上的编号不在 [ l , r ] [l,r] [l,r]之间的点的数目,复杂度 O ( log n ) O(\log n) O(logn)。
就这样吧。今日状态不佳。
#include<bits/stdc++.h>
#define ll long long
#define fi first
#define se second
#define pb push_back
#define inf 0x3f3f3f3f
using namespace std;
ll n,m,Q,a[105],b[105];
int main(){ios::sync_with_stdio(false);cin.tie(0),cout.tie(0);cin>>n>>m;for(int i=0;i<m;i++)cin>>a[i]>>b[i];cin>>Q;while(Q--){ll c,d;cin>>c>>d;ll l=1,r=n;ll numc=0,depc=0,t=0;while(1){ll M=(l*a[t]+r*b[t])/(a[t]+b[t]);if(M==c)break;if(M<c){numc++,l=M+1;}else r=M-1;t=(t+1)%m;depc++;}l=1,r=n;ll numd=0,depd=0;t=0;while(1){ll M=(l*a[t]+r*b[t])/(a[t]+b[t]);if(M==d)break;if(M>d){numd++,r=M-1;}else l=M+1;t=(t+1)%m;depd++;}ll res=2*(numc+numd+d-c)-depc-depd;cout<<res<<"\n";}
}
F - Good Division
最近只会抄 std \text{std} std了,算了摆了
首先一眼真 不难看出序列合法的充要条件是不存在绝对众数。
然后似乎也没有什么特别好的思路,不妨还是尝试一下当确定绝对众数为 v v v的情形,并且我们用总方案数减去不合法的方案数。那么将 ( a 2 i − 1 , a 2 i ) (a_{2i-1},a_{2i}) (a2i−1,a2i)看成一个权值在 [ − 1 , 1 ] [-1,1] [−1,1]之间的数(记作 b i b_i bi),我们需要对后缀和 > 0 >0 >0的位置求和。
让我们跳出这个 d p dp dp。考虑对于固定的 v v v,如果对位置 i i i造成影响,那么一定存在 j < i j<i j<i,使得 S j < S i S_j<S_i Sj<Si。分析可知,这样的 i i i不会超过 c n t v cnt_v cntv个。
同时对于一个 j j j,我们还要知道它会对那些 v v v造成贡献。显然这样的 j j j也不会超过 c n t v cnt_v cntv个。
那么将这些信息预处理出来即可。注意还是要写离散化。
复杂度 O ( n log n ) O(n\log n) O(nlogn)。
没什么状态就写一下代码吧
反思:这道题做了两个下午才 A A A掉,说明自己的代码能力还是不够(或者说想得还是不够)。应该引起重视。
#include<bits/stdc++.h>
#define ll long long
#define fi first
#define se second
#define pb push_back
#define inf 0x3f3f3f3f
using namespace std;
const int N=2e6+5;
const int mod=998244353;
int n,a[N],cnt[N],*f[N];
int bit[N*2],len,dp[N];
vector<pair<int,int>>G[N];
vector<pair<int,int>>maj[N];
vector<pair<int,int>>maj2[N];
vector<int>lsh[N];
int qry(int v,int x){int tot(0);for(;x;x-=x&-x)tot=(tot+f[v][x])%mod;return tot;
}
void upd(int v,int x,int y){for(;x<=2*cnt[v];x+=x&-x)f[v][x]=(f[v][x]+y)%mod;
}
int get(int x,int y){return lower_bound(lsh[x].begin(),lsh[x].end(),y)-lsh[x].begin()+1;
}
int main(){ios::sync_with_stdio(false);cin.tie(0),cout.tie(0);cin>>n;for(int i=1;i<=2*n;i++)cin>>a[i],cnt[a[i]]++;//fixedfor(int i=1;i<=2*n;i++)f[i]=bit+len,len+=2*cnt[i]+1;for(int i=1;i<=n;i++){if(a[2*i-1]==a[2*i]){G[a[2*i-1]].pb({i,1});}else{G[a[2*i-1]].pb({i,0});G[a[2*i]].pb({i,0});}}//fixedfor(int i=1;i<=2*n;i++){int sumnow=0,sumpre=0,pos=0,sumval=-n;for(auto x:G[i]){while(sumnow-1>sumpre&&pos+1<x.fi)sumnow--,pos++,maj[pos].pb({i,sumnow}),lsh[i].pb(sumnow);sumnow-=x.fi-pos-1;//全是-1sumpre=min(sumpre,sumnow);pos=x.fi;if((sumnow+=x.se)>sumpre)maj[x.fi].pb({i,sumnow}),lsh[i].pb(sumnow);sumval+=1+x.se;}while(sumnow-1>sumpre&&pos+1<=n)sumnow--,pos++,maj[pos].pb({i,sumnow}),lsh[i].pb(sumnow);reverse(G[i].begin(),G[i].end());sumnow=0,sumpre=0,pos=n+1;for(auto x:G[i]){while(sumnow-1>sumpre&&pos-1>x.fi)sumnow--,pos--,maj2[pos-1].pb({i,sumval-sumnow}),lsh[i].pb(sumval-sumnow);sumnow-=pos-x.fi-1;sumpre=min(sumpre,sumnow);pos=x.fi;if((sumnow+=x.se)>sumpre){maj2[pos-1].pb({i,sumval-sumnow}),lsh[i].pb(sumval-sumnow);}}while(sumnow-1>sumpre&&pos-1>=1)sumnow--,pos--,maj2[pos-1].pb({i,sumval-sumnow}),lsh[i].pb(sumval-sumnow);sort(lsh[i].begin(),lsh[i].end());lsh[i].erase(unique(lsh[i].begin(),lsh[i].end()),lsh[i].end());}//fixedint sumpre=1;for(int i=0;i<=n;i++){dp[i]=sumpre;for(auto x:maj[i]){dp[i]=(dp[i]-qry(x.fi,get(x.fi,x.se)-1))%mod;}for(auto x:maj2[i]){upd(x.fi,get(x.fi,x.se),dp[i]);}if(i)sumpre=(sumpre+dp[i])%mod;}cout<<(dp[n]+mod)%mod<<"\n";
}
相关文章:

【学习笔记】ARC159
D - LIS 2 因为没有让你求方案数,所以还是比较好做的。 如果每一个连续段都退化成一个点,那么答案就是直接求 L I S LIS LIS。 否则,假设我们选了一些连续段把它们拼起来形成答案,显然我们有 r i 1 ≥ l i r_{i1}\ge l_i ri1…...

2023/4/16总结
图的存储 链式前向星 链式前向星和邻接表很相似,只是存储方式变成了数组。 链式前向星一般要用到一个结构体数组和一个一维数组,结构体数组edges中包括三个变量。结构体数组的大小一般由边的大小决定。 edges数组中的to代表的是某条边的终点v。w代表的是这条边的…...

【剑指offer】常用的数据增强的方法
系列文章目录 BN层详解 梯度消失和梯度爆炸 交叉熵损失函数 反向传播 1*1卷积的作用 文章目录 系列文章目录常用的数据增强的方法示例代码 常用的数据增强的方法 数据增强是指通过对原始数据进行一系列变换来生成更多的训练数据,从而提高模型的泛化能力。常用的数…...

/lib/lsb/init-functions文件解析
零、背景 在玩AppArmor的时候涉及到了/etc/init.d/apparmor(无论是sudo /etc/init.d/apparmor start还是sudo systemctl start apparmor.service),而这个文件又涉及到了另一个文件、也就是本文的主角:/lib/lsb/init-functions。 …...

【ChatGPT】ChatGPT-5 强到什么地步?
Yan-英杰的主页 悟已往之不谏 知来者之可追 C程序员,2024届电子信息研究生 目录 ChatGPT-5 强到什么地步? 技术 深度学习模型的升级 更好的预测能力 自适应学习能力 特点 语言理解能力更强 自我修正和优化 更广泛的应用领域 应用 对话系统 智能写作…...
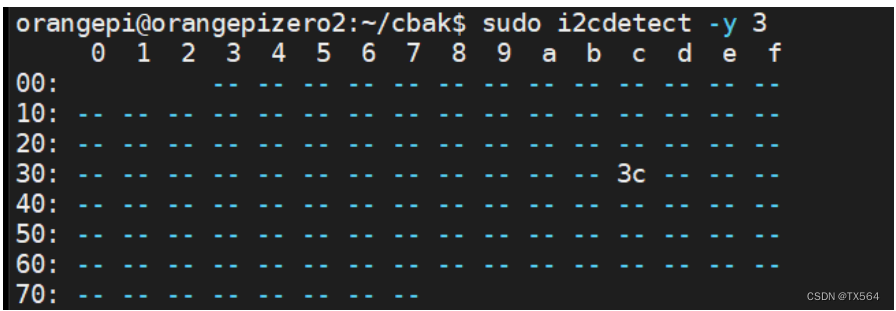
[ARM+Linux] 基于全志h616外设开发笔记
修改用户密码 配置网络 nmcli dev wifi 命令扫描周围WIFI热点 nmcli dev wifi connect xxx password xxx 命令连接WiFi 查看ip地址的指令: ifconfig ip addr show wlan0 SSH登录 这是企业开发调试必用方式,比串口来说不用接线,前提是接入网络…...
如何实现24小时客户服务
许多企业都有着这样的愿望:在不增加客服人员的同时能实现24小时客户服务。 那么有没有什么方法可以实现这一想法呢?在想解决方案之前我们可以先来谈谈客服的作用。 客服的作用主要为以下2点: 帮助用户更快地了解产品(减轻产品的…...
)
查询数据库空间(mysql和oracle)
Mysql版 1、查看所有数据库容量大小 -- 查看所有数据库容量大小 SELECTtable_schema AS 数据库,sum( table_rows ) AS 记录数,sum(TRUNCATE ( data_length / 1024 / 1024, 2 )) AS 数据容量(MB),sum(TRUNCATE ( index_length / 1024 / 1024, 2 )) AS 索引容量(MB) FROMinfor…...

为什么 SQLite 一定要用 C 语言来开发?
SQLite 是一种专门为在 Unix 和类 Unix 操作系统上运行的 Linux 服务器应用程序而设计的数据库管理系统,是一种轻量级的关系型数据库管理系统,它适用于许多嵌入式设备和物联网设备。它使用 C 语言编写,并且是一个开源项目。 简单易用&#x…...

TensorFlow Lite,ML Kit 和 Flutter 移动深度学习:6~11
原文:Mobile Deep Learning with TensorFlow Lite, ML Kit and Flutter 协议:CC BY-NC-SA 4.0 译者:飞龙 本文来自【ApacheCN 深度学习 译文集】,采用译后编辑(MTPE)流程来尽可能提升效率。 不要担心自己的…...

你的GPT跟ChatGPT可能只差了一个DPU
“人类永远不会嫌网络太快,就像永远不会嫌高铁太快,你只会嫌它慢,希望它更快些。” 一个月内,百度、阿里、腾讯、商汤、讯飞、360等国内大厂扎堆发布“中国版 GPT ”,这家的名字还没记清楚,另一家的又蹦了出…...
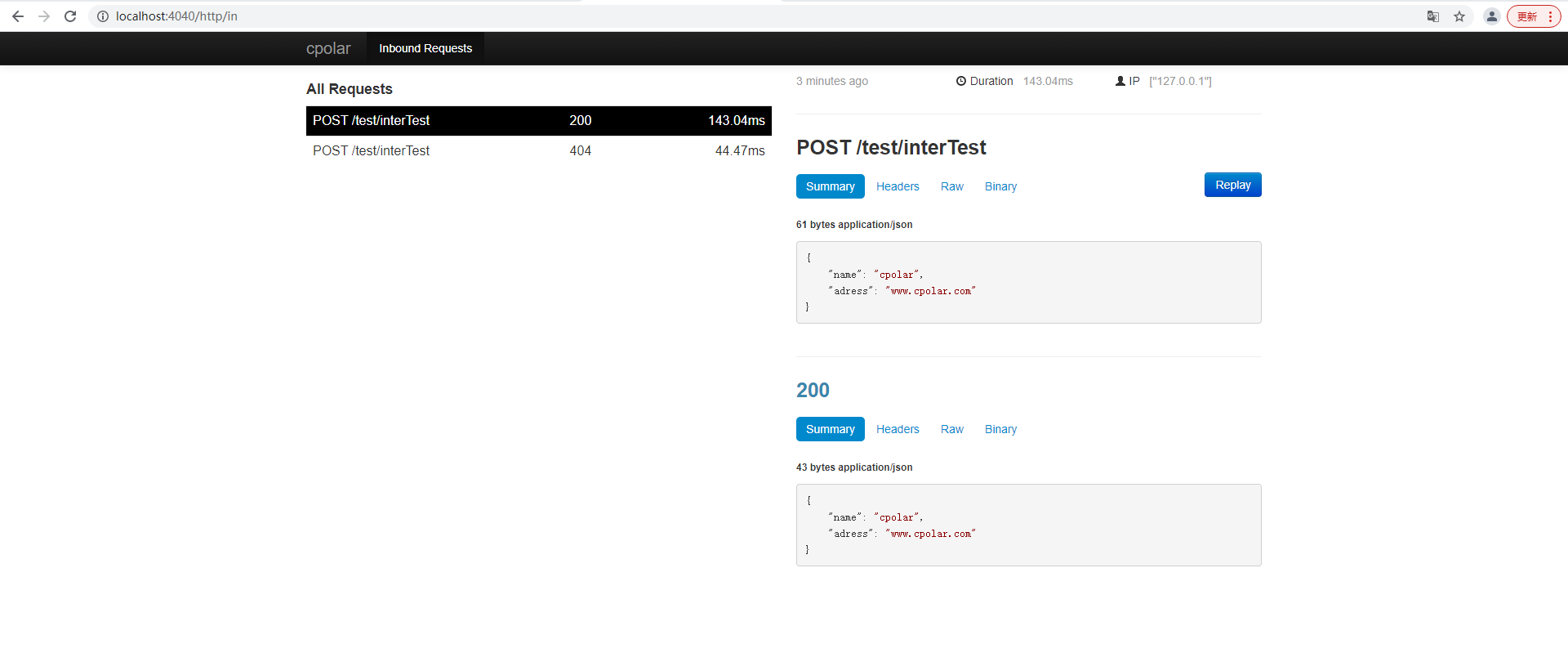
springboot服务端接口外网远程调试,并实现HTTP服务监听 - 内网穿透
文章目录 前言1. 本地环境搭建1.1 环境参数1.2 搭建springboot服务项目 2. 内网穿透2.1 安装配置cpolar内网穿透2.1.1 windows系统2.1.2 linux系统 2.2 创建隧道映射本地端口2.3 测试公网地址 3. 固定公网地址3.1 保留一个二级子域名3.2 配置二级子域名3.2 测试使用固定公网地址…...

NumPy的应用-1
准备工作 在Python中使用NumPy时,需要先安装NumPy。可以使用以下命令来安装NumPy: pip install numpy安装完成后,在Python中引入NumPy: import numpy as np安装完成并引入NumPy后,我们可以开始使用NumPy进行数据分析…...

k8s的yaml文件中kind类型详解
在Kubernetes(k8s)的YAML语法中,kind是一种重要的关键字,它用于指定Kubernetes资源的类型。根据Kubernetes官方文档,以下是kind可能的取值: Deployment:用于定义应用程序的声明式更新。Statefu…...

第三天:C语言控制结构
目录 1. 条件语句 2. 循环语句 3. 实例:计算阶乘 在前两天的学习中,您已经掌握了C语言的基本知识。今天,我们将学习C语言的控制结构,包括条件语句和循环语句。通过控制结构,您可以实现程序的分支和循环,…...
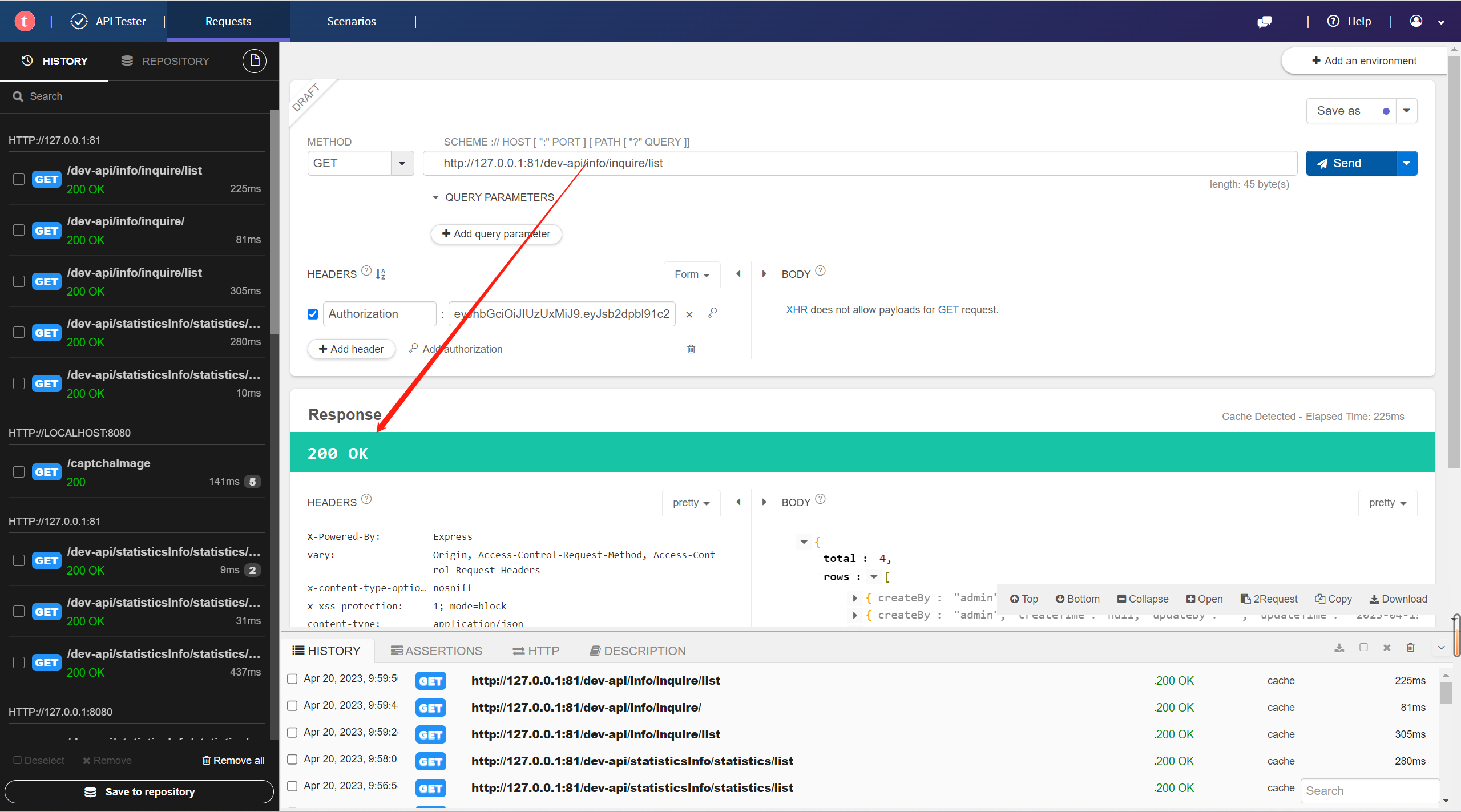
访问若依vue版后端api接口
访问若依vue版后端api接口 如何使用Talend API Tester进行访问若依vue-前后端分离版的后端api接口? 方法一: 写好一个后台api接口,启动项目 直接使用Talend API Tester进行访问后台api出现如下错误,原因是因为若依系统有jwt认证…...
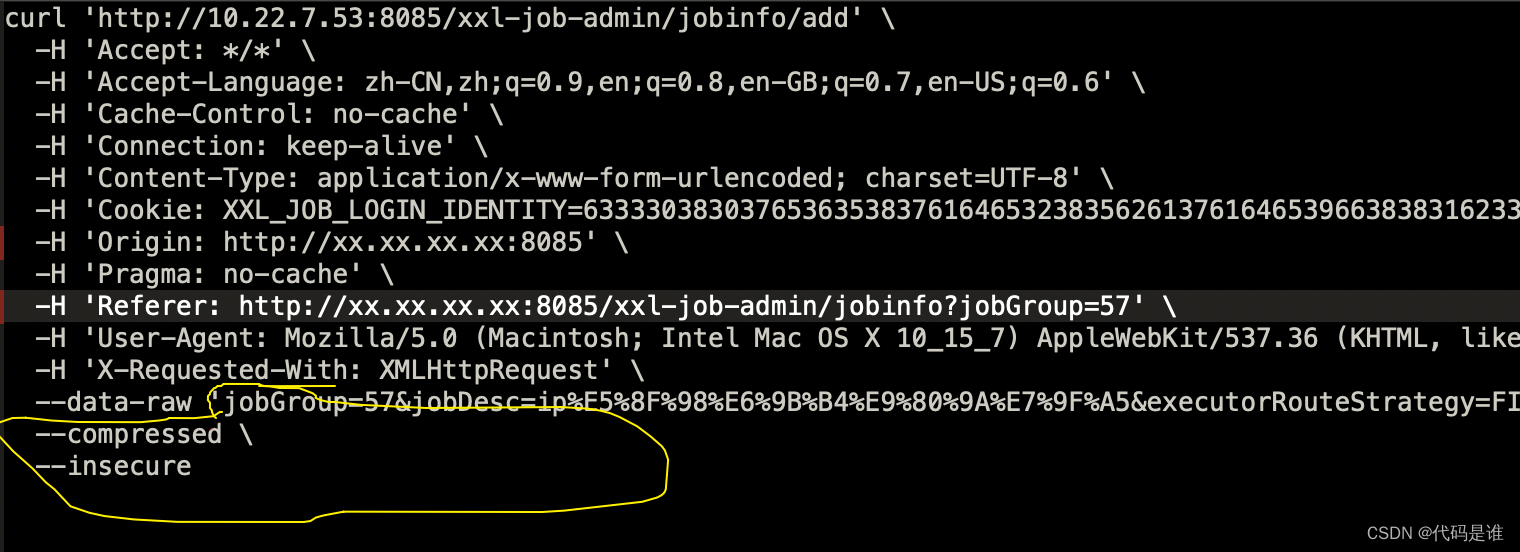
另一种迁移xxl-job任务的方法,适合不满足数据迁移条件
以为多个项目组同时使用一个xxl-job,同时涉及到版本提升,由此不太满足数据库数据迁移,所以这里提供另一种解决办法 使用工具:postman,json转excel,excel 核心:excel拼接: 1.使用f12抓取xxl任务访…...
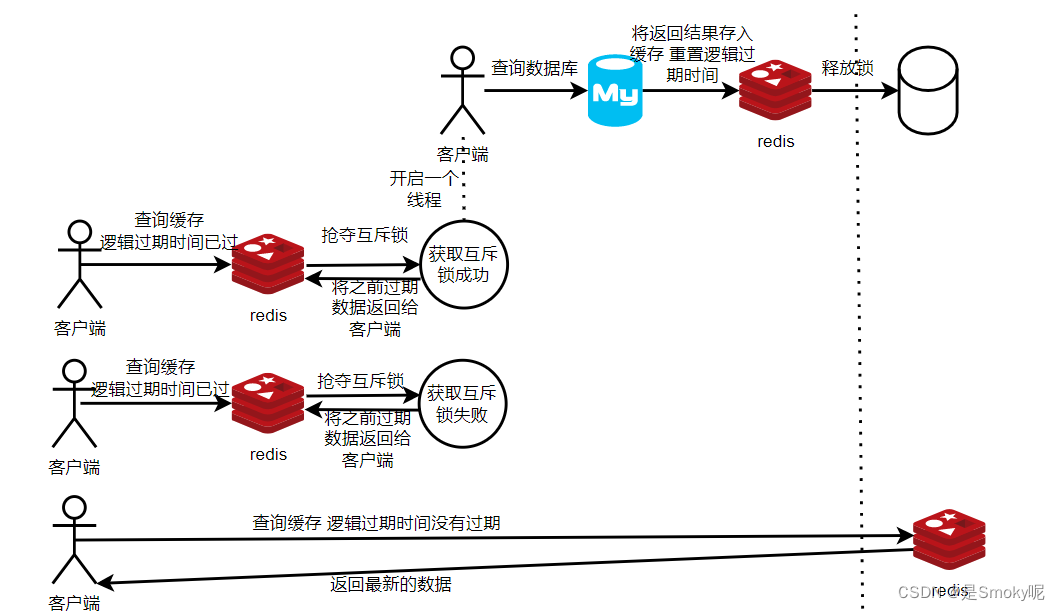
Redis缓存穿透、击穿、雪崩面试题详解
缓存穿透 问题: 指的是客户端请求的数据在缓存中找不到,数据库中也没有存储,客户端还不断的发起请求。这样每次都无法在数据库查询到,缓存中永远没有这个数据。 这样的话,客户端一直去访问,会给后端数据…...
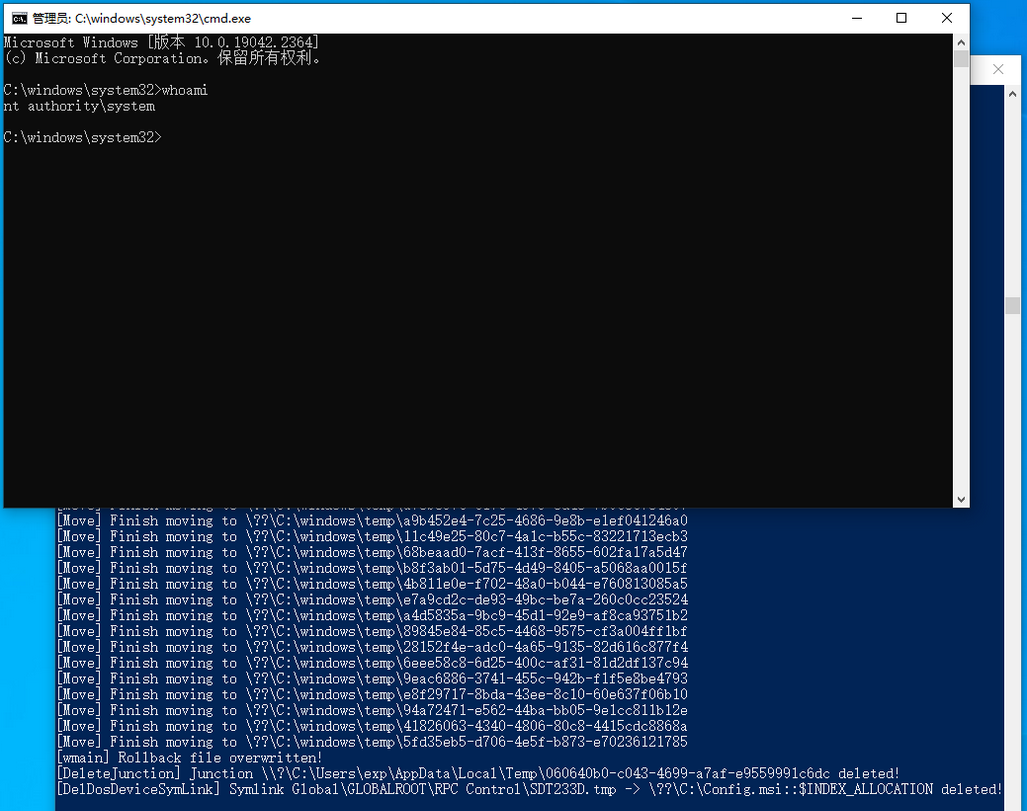
【网络安全】本地提权漏洞分析
0. 前言 CVE-2023-21752 是 2023 年开年微软第一个有 exploit 的漏洞,原本以为有利用代码会很好分析,但是结果花费了很长时间,难点主要了两个:漏洞点定位和漏洞利用代码分析,欢迎指正。 1. 漏洞简介 根据官方信息&a…...

电脑端(PC)按键精灵——3.其他命令
电脑端(PC)按键精灵——3.其他命令 前两节说了安装、键盘和鼠标命令,这一章说下其他命令 按键精灵小白入门详细教程: 电脑端(PC)按键精灵—小白入门 详细教程 命令介绍 1. Delay 延时 简介 //1秒=1000毫秒, 1分钟=60000毫秒,…...

(十)学生端搭建
本次旨在将之前的已完成的部分功能进行拼装到学生端,同时完善学生端的构建。本次工作主要包括: 1.学生端整体界面布局 2.模拟考场与部分个人画像流程的串联 3.整体学生端逻辑 一、学生端 在主界面可以选择自己的用户角色 选择学生则进入学生登录界面…...
使用rpicam-app通过网络流式传输视频)
树莓派超全系列教程文档--(62)使用rpicam-app通过网络流式传输视频
使用rpicam-app通过网络流式传输视频 使用 rpicam-app 通过网络流式传输视频UDPTCPRTSPlibavGStreamerRTPlibcamerasrc GStreamer 元素 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 使用 rpicam-app 通过网络流式传输视频 本节介绍来自 rpica…...

逻辑回归:给不确定性划界的分类大师
想象你是一名医生。面对患者的检查报告(肿瘤大小、血液指标),你需要做出一个**决定性判断**:恶性还是良性?这种“非黑即白”的抉择,正是**逻辑回归(Logistic Regression)** 的战场&a…...
)
IGP(Interior Gateway Protocol,内部网关协议)
IGP(Interior Gateway Protocol,内部网关协议) 是一种用于在一个自治系统(AS)内部传递路由信息的路由协议,主要用于在一个组织或机构的内部网络中决定数据包的最佳路径。与用于自治系统之间通信的 EGP&…...

WordPress插件:AI多语言写作与智能配图、免费AI模型、SEO文章生成
厌倦手动写WordPress文章?AI自动生成,效率提升10倍! 支持多语言、自动配图、定时发布,让内容创作更轻松! AI内容生成 → 不想每天写文章?AI一键生成高质量内容!多语言支持 → 跨境电商必备&am…...

在web-view 加载的本地及远程HTML中调用uniapp的API及网页和vue页面是如何通讯的?
uni-app 中 Web-view 与 Vue 页面的通讯机制详解 一、Web-view 简介 Web-view 是 uni-app 提供的一个重要组件,用于在原生应用中加载 HTML 页面: 支持加载本地 HTML 文件支持加载远程 HTML 页面实现 Web 与原生的双向通讯可用于嵌入第三方网页或 H5 应…...

AGain DB和倍数增益的关系
我在设置一款索尼CMOS芯片时,Again增益0db变化为6DB,画面的变化只有2倍DN的增益,比如10变为20。 这与dB和线性增益的关系以及传感器处理流程有关。以下是具体原因分析: 1. dB与线性增益的换算关系 6dB对应的理论线性增益应为&…...

比较数据迁移后MySQL数据库和OceanBase数据仓库中的表
设计一个MySQL数据库和OceanBase数据仓库的表数据比较的详细程序流程,两张表是相同的结构,都有整型主键id字段,需要每次从数据库分批取得2000条数据,用于比较,比较操作的同时可以再取2000条数据,等上一次比较完成之后,开始比较,直到比较完所有的数据。比较操作需要比较…...

提升移动端网页调试效率:WebDebugX 与常见工具组合实践
在日常移动端开发中,网页调试始终是一个高频但又极具挑战的环节。尤其在面对 iOS 与 Android 的混合技术栈、各种设备差异化行为时,开发者迫切需要一套高效、可靠且跨平台的调试方案。过去,我们或多或少使用过 Chrome DevTools、Remote Debug…...

LCTF液晶可调谐滤波器在多光谱相机捕捉无人机目标检测中的作用
中达瑞和自2005年成立以来,一直在光谱成像领域深度钻研和发展,始终致力于研发高性能、高可靠性的光谱成像相机,为科研院校提供更优的产品和服务。在《低空背景下无人机目标的光谱特征研究及目标检测应用》这篇论文中提到中达瑞和 LCTF 作为多…...
