【机会约束、鲁棒优化】机会约束和鲁棒优化研究优化【ccDCOPF】研究(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥
🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。
⛳️座右铭:行百里者,半于九十。
📋📋📋本文目录如下:🎁🎁🎁
目录
💥1 概述
📚2 运行结果
🎉3 参考文献
🌈4 Matlab代码实现
💥1 概述
随机规划的三个分支分别为期望值模型、机会约束规划和相关机会规划。机会约束规划是继期望值模型之后,由A. Charnes和 W.W. Cooper于 1959年提出的第二类随机规划[33]。CCP是考虑到所做决策在不利情况发生时可能不满足约束条件而采用的一种原则:即允许所做决策在一定程度上不满足约束条件,但该决策使约束条件成立的概率不小于某一置信水平。一般形式的机会约束可表示为: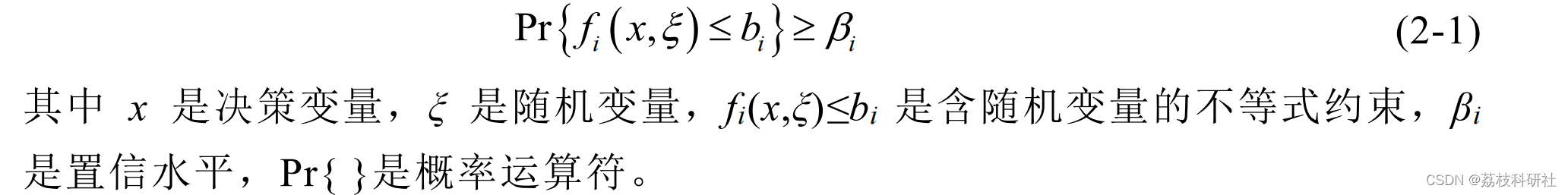
CCP 是处理随机规划问题的经典方法之一,其主要利用概率形式约束处理约束条件中含有随机变量的优化问题,CCP 方法具有以下特点:
(1)为了有效处理含随机变量的约束问题,CCP 将传统规划模型中的硬约束变为概率形式约束,以实现考虑随机变量的大概率事件,减小低概率极端事件对最优解的影响,一定程度上提高了最优解的合理性。
(2)对于问题中的随机变量,仅在约束中以机会约束的形式进行体现,未在目标函数中予以反映,而规划问题的最优解与概率约束的置信水平直接相关,且其置信水平可根据决策者的风险偏好或实际经验进行设定。
(3)当模型中含有多个机会约束时,在优化过程中将予以同等对待,无主次顺序之分。
(4)CCP 模型的求解过程中常需利用 MCS 过程和智能算法,其求解过程较为复杂,求解效率与结果质量都受到一定影响;若通过解析法求解则需较复杂的数学推导,以上因素在一定程度上了限制了 CCP 方法在复杂问题中的应用。
📚2 运行结果
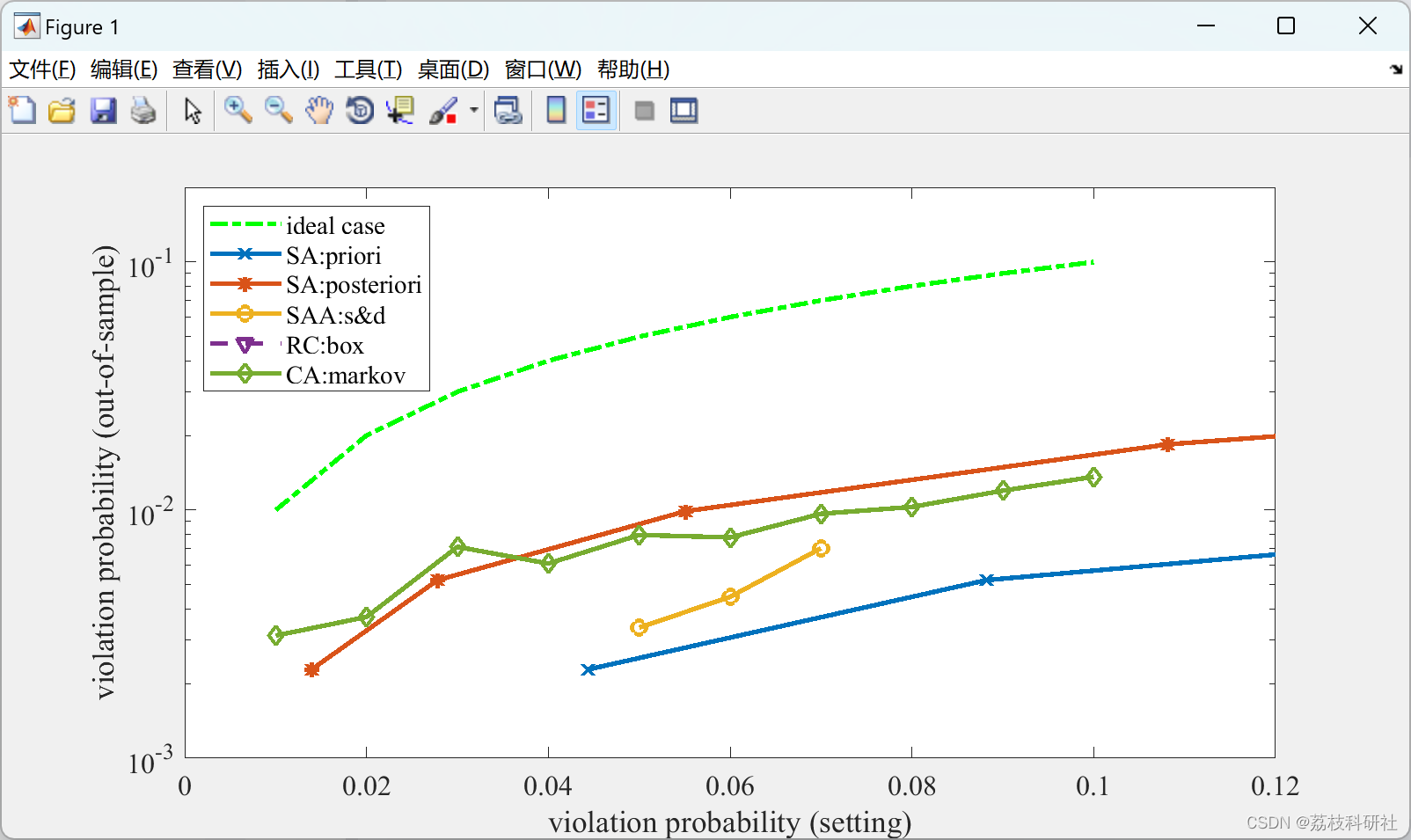
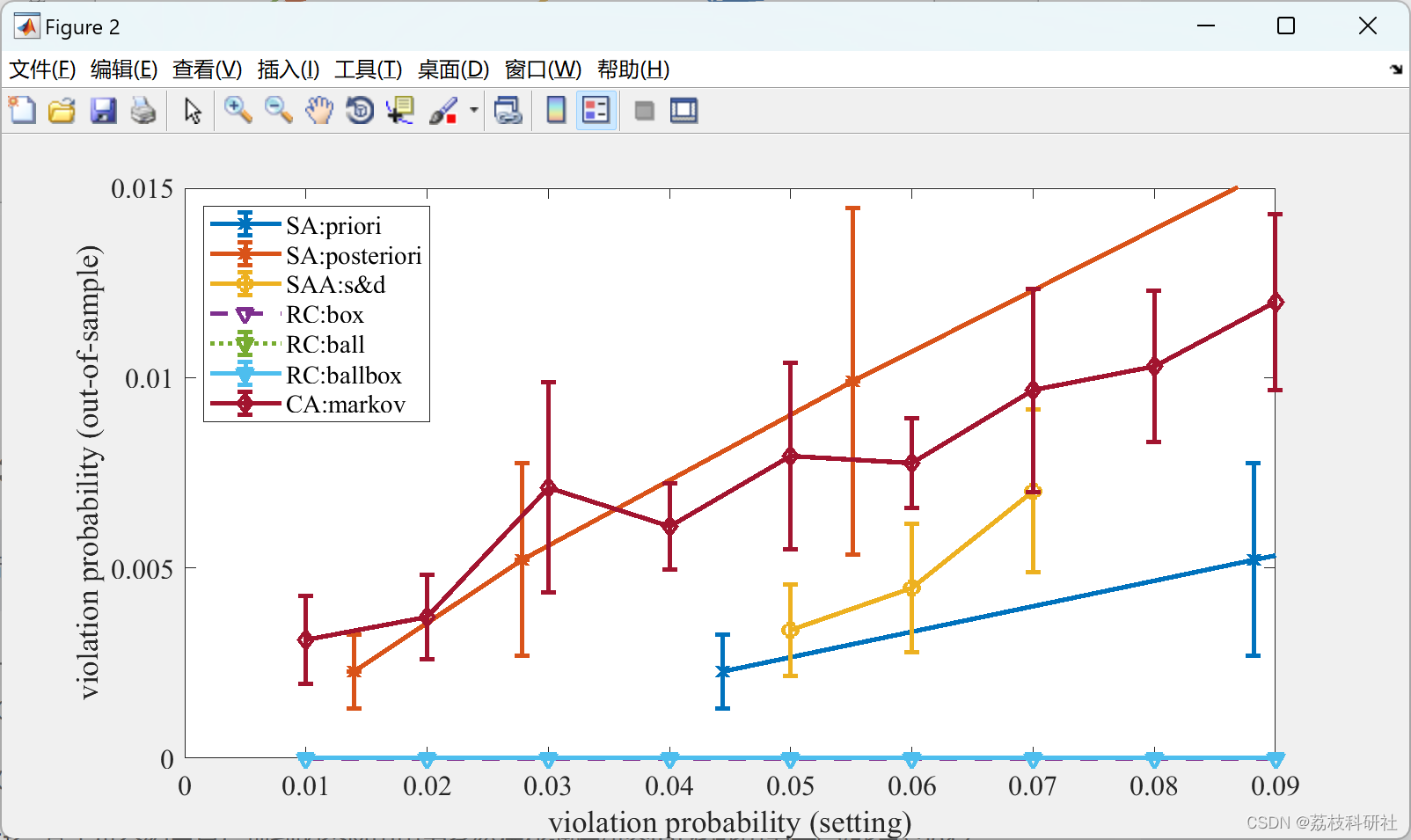
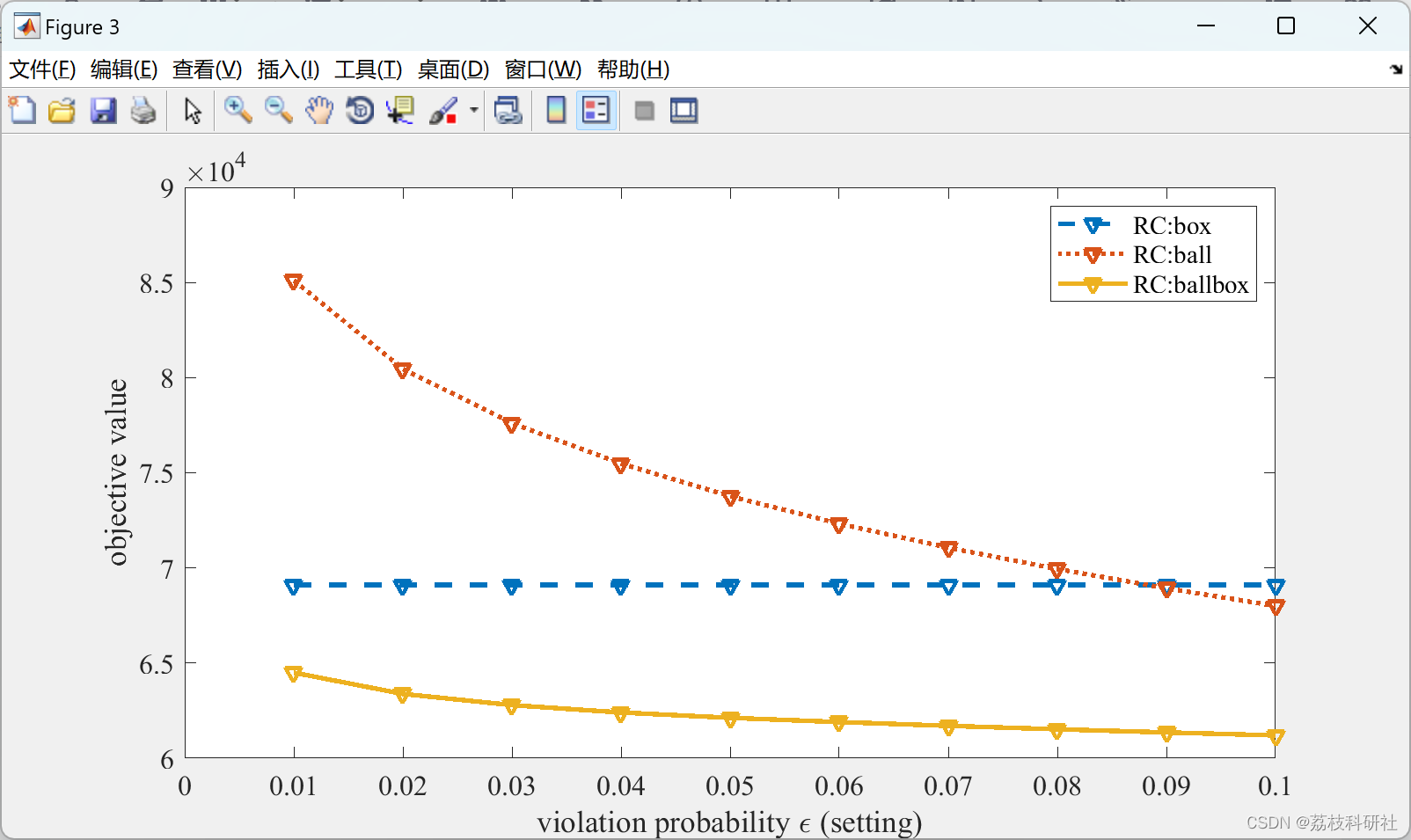
部分代码:
clear; clc; close all;
fig_size = [10,10,800,400];
beta = 10^(-2);
% casename = 'ex_case3sc'; N = 100;
casename = 'ex_case24_ieee_rts'; N = 2048;
eps_scale = 0.01:0.01:0.1;
result_sa = load([casename,'-scenario approach-results.mat']);
result_ca = load([casename,'-convex approximation-type-results-N=',num2str(N),'.mat']);
result_saa = load([casename,'-sample average approximation-sampling and discarding-results-N=',num2str(N),'.mat']);
result_rc = load([casename,'-robust counterpart-results-N=',num2str(N),'.mat']);
% result_lb = load([casename,'-obj-lower-bound.mat']);
f_eps = figure('Position', fig_size);
lgd_str = {};
plot(eps_scale,eps_scale,'g-.','LineWidth',2), hold on, lgd_str = [lgd_str,'ideal case'];
plot(nanmean(result_sa.eps_pri,2), nanmean(result_sa.eps_empirical,2),'-x','LineWidth',2), hold on, lgd_str = [lgd_str,'SA:priori'];
plot(nanmean(result_sa.eps_post,2), nanmean(result_sa.eps_empirical,2),'-*','LineWidth',2), hold on, lgd_str = [lgd_str,'SA:posteriori'];
plot(result_saa.epsilons, nanmean(result_saa.eps_empirical,2),'-o','LineWidth',2), hold on, lgd_str = [lgd_str,'SAA:s&d'];
plot(result_rc.eps, nanmean(result_rc.eps_empirical_box,2)*ones(size(result_rc.eps)),'--v','LineWidth',2), hold on, lgd_str = [lgd_str,'RC:box'];
% plot(result_rc.eps, nanmean(result_rc.eps_empirical_ball,2),':v','LineWidth',2), hold on, lgd_str = [lgd_str,'RC:ball'];
% plot(result_rc.eps, nanmean(result_rc.eps_empirical_ballbox,2),'-v','LineWidth',2), hold on, lgd_str = [lgd_str,'RC:ballbox'];
% plot(result_rc.eps, nanmean(result_rc.eps_empirical_budget,2),'-.v','LineWidth',2), hold on, lgd_str = [lgd_str,'RC:budget'];
plot(result_ca.eps, nanmean(result_ca.eps_empirical,2),'-d','LineWidth',2), hold on, lgd_str = [lgd_str,'CA:markov'];
legend(lgd_str,'Location','NorthWest')
set(gca,'yscale','log')
% xlim([0,0.9]), ylim([1e-4 10])
xlim([0,0.12]), ylim([1e-3 0.2])
xlabel('violation probability (setting)'),ylabel('violation probability (out-of-sample)')
set(gca,'FontSize',12,'fontname','times')
print(f_eps,'-depsc','-painters',[casename,'-all-methods-epsilon.eps'])
f_eps_err = figure('Position', fig_size);
lgd_str = {};
% plot(eps_scale,eps_scale,'g-.','LineWidth',2), hold on, lgd_str = [lgd_str,'ideal case'];
errorbar(nanmean(result_sa.eps_pri,2), nanmean(result_sa.eps_empirical,2),nanstd(result_sa.eps_empirical,[],2),'-x','LineWidth',2), hold on, lgd_str = [lgd_str,'SA:priori'];
errorbar(nanmean(result_sa.eps_post,2), nanmean(result_sa.eps_empirical,2),nanstd(result_sa.eps_empirical,[],2),'-*','LineWidth',2), hold on, lgd_str = [lgd_str,'SA:posteriori'];
errorbar(result_saa.epsilons, nanmean(result_saa.eps_empirical,2),nanstd(result_saa.eps_empirical,[],2),'-o','LineWidth',2), hold on, lgd_str = [lgd_str,'SAA:s&d'];
plot(result_rc.eps, nanmean(result_rc.eps_empirical_box,2)*ones(size(result_rc.eps)),'--v','LineWidth',2), hold on, lgd_str = [lgd_str,'RC:box'];
errorbar(result_rc.eps, nanmean(result_rc.eps_empirical_ball,2),nanstd(result_rc.eps_empirical_ball,[],2),':v','LineWidth',2), hold on, lgd_str = [lgd_str,'RC:ball'];
errorbar(result_rc.eps, nanmean(result_rc.eps_empirical_ballbox,2),nanstd(result_rc.eps_empirical_ballbox,[],2),'-v','LineWidth',2), hold on, lgd_str = [lgd_str,'RC:ballbox'];
% errorbar(result_rc.eps, nanmean(result_rc.eps_empirical_budget,2),nanstd(result_rc.eps_empirical_budget,[],2),'-.v','LineWidth',2), hold on,
errorbar(result_ca.eps, nanmean(result_ca.eps_empirical,2), nanstd(result_ca.eps_empirical,[],2),'-d','LineWidth',2), hold on, lgd_str = [lgd_str,'CA:markov'];
legend(lgd_str,'Location','NorthWest')
% xlim([0,0.12])
xlim([0,0.09])
% ylim([0,0.09])
xlabel('violation probability (setting)'),ylabel('violation probability (out-of-sample)')
set(gca,'FontSize',12,'fontname','times')
print(f_eps_err,'-depsc','-painters',[casename,'-all-methods-epsilon-errorbar.eps'])
f_obj = figure('Position', fig_size);
lgd_str = {};
% plot(result_lb.epsilons, result_lb.obj_low, ':^'), hold on,
% plot(nanmean(result_sa.eps_pri,2), nanmean(result_sa.obj,2),'-x','LineWidth',2), hold on, lgd_str = [lgd_str,'SA:priori'];
% plot(nanmean(result_sa.eps_post,2), nanmean(result_sa.obj,2),'-*','LineWidth',2), hold on, lgd_str = [lgd_str,'SA:posteriori'];
% plot(result_saa.epsilons, nanmean(result_saa.obj,2),'-o','LineWidth',2), hold on, lgd_str = [lgd_str,'SAA:s&d'];
plot(result_rc.eps, nanmean(result_rc.obj_box,2)*ones(size(result_rc.eps)),'--v','LineWidth',2), hold on, lgd_str = [lgd_str,'RC:box'];
plot(result_rc.eps, nanmean(result_rc.obj_ball,2),':v','LineWidth',2), hold on, lgd_str = [lgd_str,'RC:ball'];
plot(result_rc.eps, nanmean(result_rc.obj_ballbox,2),'-v','LineWidth',2), hold on, lgd_str = [lgd_str,'RC:ballbox'];
% plot(result_rc.eps, nanmean(result_rc.obj_budget,2),'-.v','LineWidth',2), hold on,
% plot(result_ca.eps, nanmean(result_ca.obj, 2),'-d','LineWidth',2), hold on, lgd_str = [lgd_str,'CA:markov'];
legend(lgd_str)
xlabel('violation probability \epsilon (setting)'),ylabel('objective value')
xlim([0 0.1])
set(gca,'FontSize',12,'fontname','times')
print(f_obj,'-depsc','-painters',[casename,'-all-methods-objective.eps'])
% f_obj_emp = figure('Position', fig_size);
% % plot(result_lb.epsilons, result_lb.obj_low,'-^'), hold on,
% [result_sa_eps_empirical,indices] = sort( nanmean(result_sa.eps_empirical,2),'ascend' );
% plot(result_sa_eps_empirical, nanmean(result_sa.obj(indices,:),2),'-v'), hold on,
% [result_saa_eps_empirical,indices] = sort( nanmean(result_saa.eps_empirical,2),'ascend' );
% plot(result_saa_eps_empirical, nanmean(result_saa.obj(indices,:),2),'-d'), hold on,
% [result_rc_eps_empirical_box,indices] = sort( nanmean(result_rc.eps_empirical_box,2),'ascend' );
% plot(result_rc_eps_empirical_box, nanmean(result_rc.obj_box(indices,:),2),'-*'), hold on,
% [result_rc_eps_empirical_ball,indices] = sort( nanmean(result_rc.eps_empirical_ball,2),'ascend' );
% plot(result_rc_eps_empirical_ball, nanmean(result_rc.obj_ball(indices,:),2),'-*'), hold on,
% [result_rc_eps_empirical_ballbox,indices] = sort( nanmean(result_rc.eps_empirical_ballbox,2),'ascend' );
% plot(result_rc_eps_empirical_ballbox, nanmean(result_rc.obj_ballbox(indices,:),2),'-x'), hold on,
% [result_rc_eps_empirical_budget,indices] = sort( nanmean(result_rc.eps_empirical_budget,2),'ascend' );
% plot(result_rc_eps_empirical_budget, nanmean(result_rc.obj_budget(indices,:),2),'-x'), hold on,
% [result_ca_eps_empirical,indices] = sort( nanmean(result_ca.eps_empirical,2),'ascend' );
% plot(result_ca_eps_empirical, nanmean(result_ca.obj,2),'-d','LineWidth',2), hold on,
% % legend('lower bound','SA','SAA:s&d','RC:box','RC:ball','RC:ballbox','RC:budget')
% legend('SA','SAA:s&d','RC:box','RC:ball','RC:ballbox','RC:budget','CA:markov')
% set(gca,'xscale','log')
% xlim([0 0.06])
🎉3 参考文献
部分理论来源于网络,如有侵权请联系删除。
[1]付波,邓竞成,康毅恒.基于机会约束的园区综合能源系统优化调度[J].湖北工业大学学报,2023,38(01):11-14+32.
[2]耿晓路. 分布鲁棒机会约束优化问题的研究[D].湘潭大学,2018.
[3]王扬. 基于机会约束目标规划的含风电电力系统优化调度研究[D].华北电力大学(北京),2017.
🌈4 Matlab代码实现
相关文章:

【机会约束、鲁棒优化】机会约束和鲁棒优化研究优化【ccDCOPF】研究(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...

4月想跳槽的同学,没有更好的选择,可以去美团
在美团干了半年,说一下自己的感受,美团是一家福利中等,工资待遇中上,高层管理团队强大,加班强度一般,技术不错,办公环境一般,工作氛围中上,部门差距之间工作体验差距巨大…...
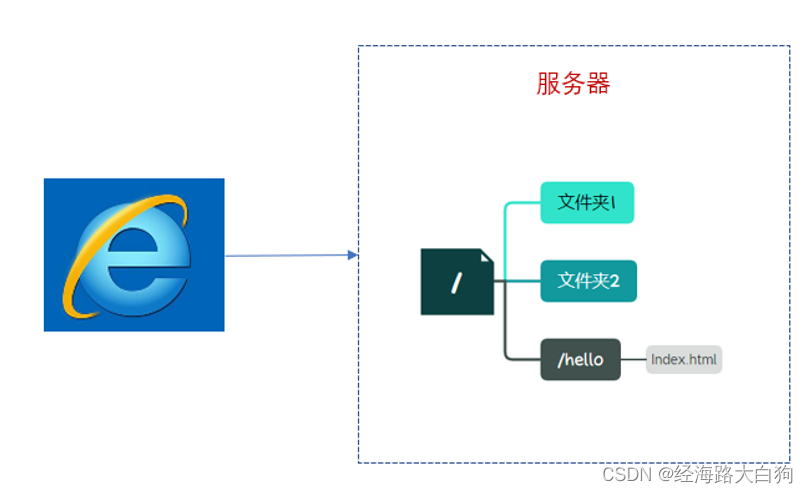
从输入url到页面展现(一)从浏览器解析url开始
前端面试有一道很考验人的问题,那就是:请你说一下从用户从输入url到页面展现的过程是怎样的?在接下来的一段时间呢,狗哥会从这一问题出发,开始剖析这个过程,希望可以让更多的小伙伴掌握到这个过程ÿ…...

购物 · 礼物
标题 前言必学场景词汇及用法书店花店玩具店讨价还价情境常用单词书店花店玩具店前言 加油 必学场景词汇及用法 书店 1.book store / book shop 书店 I browsed through the book store, but I didn’t find the book I was looking for. 我把书店里的书浏览了一番,但是没…...
)
可视化图表API格式要求有哪些?Sugar BI详细代码示例(2)
Sugar BI中的每个图表可以对应一个数据 API,用户浏览报表时,选定一定的过滤条件,点击「查询」按钮将会通过 API 拉取相应的数据;前面说过,为了确保用户数据的安全性,Sugar BI上的所有数据请求都在Sugar BI的…...
153. 寻找旋转排序数组中的最小值
已知一个长度为 n 的数组,预先按照升序排列,经由 1 到 n 次 旋转 后,得到输入数组。例如,原数组 nums [0,1,2,4,5,6,7] 在变化后可能得到: 若旋转 4 次,则可以得到 [4,5,6,7,0,1,2] 若旋转 7 次࿰…...
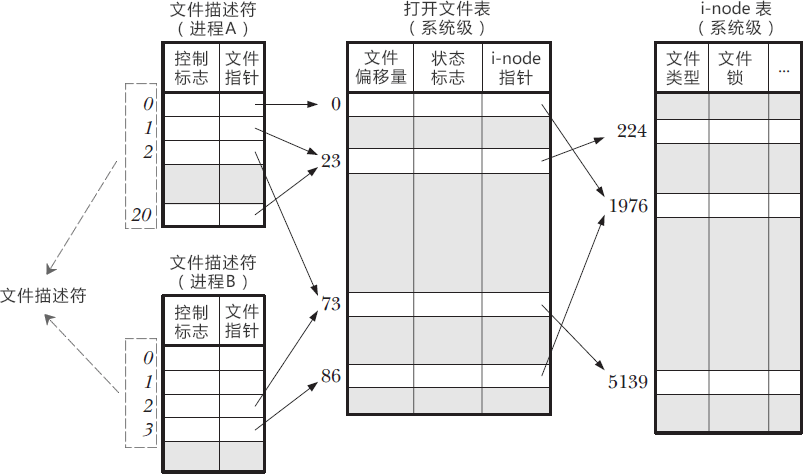
Linux 文件描述符
Linux 文件描述符 Linux 中一切皆文件,比如 C 源文件、视频文件、Shell脚本、可执行文件等,就连键盘、显示器、鼠标等硬件设备也都是文件。 一个 Linux 进程可以打开成百上千个文件,为了表示和区分已经打开的文件,Linux 会给每个…...

第17章_反射机制
第17章_反射机制 讲师:尚硅谷-宋红康(江湖人称:康师傅) 官网:http://www.atguigu.com 本章专题与脉络 1. 反射(Reflection)的概念 1.1 反射的出现背景 Java程序中,所有的对象都有两种类型:编…...

使用VBA小程序提高资产清查效率
资产清查是一件相当烦人的工作,去年使用LayUIPHPMS SQL Server 2014写了一个资产清查的程序,可惜写完了,LayUI已经停止更新了,就没有再完善下去,数据也没有更新,等于就废了。 今年又要进行资产清查…...

JavaSE学习进阶day07_02 异常
第三章 异常 3.1 异常概念 异常,就是不正常的意思。在生活中:医生说,你的身体某个部位有异常,该部位和正常相比有点不同,该部位的功能将受影响.在程序中的意思就是: 异常 :指的是程序在执行过程中,出现的非正常的情况࿰…...
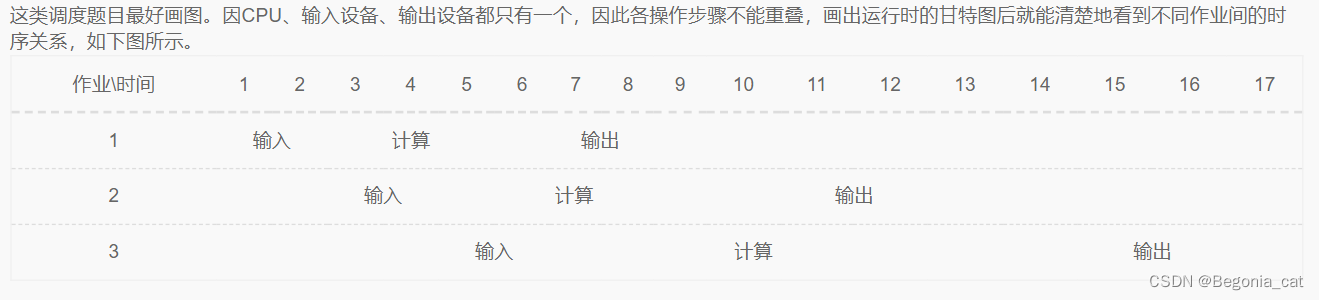
操作系统学习笔记
文章目录 操作系统虚拟内存锁缓存机制CPU性能指标进程、线程文件管理系统 操作系统 操作系统是控制应用程序的执行,并充当应用程序和计算机硬件之间的接口。在计算机系统中,处于最外层的是(应用软件) 。 面向用户的就是外层的&am…...

【Spring Boot】SpringBoot设计了哪些可拓展的机制?
文章目录 前言SpringBoot核心源码拓展Initializer拓展监听器ApplicationListenerBeanFactory的后置处理器 & Bean的后置处理器AOP其他的拓展点 前言 当我们引入注册中心的依赖,比如nacos的时候,当我们启动springboot,这个服务就会根据配置…...

《程序员面试金典(第6版)》面试题 10.10. 数字流的秩
题目描述 假设你正在读取一串整数。每隔一段时间,你希望能找出数字 x 的秩(小于或等于 x 的值的个数)。请实现数据结构和算法来支持这些操作,也就是说: 实现 track(int x) 方法,每读入一个数字都会调用该方法; 实现 g…...

智能洗地机好用吗?值得入手的洗地机推荐
洗地机是一款高效的地面清洁设备,不仅可以很好清理地面不同形态的干湿垃圾,还减少了人工和水资源的浪费,是我们日常生活中必不可少的清洁工具。作为以一位评测博主,很多朋友咨询我在选购洗地机时应该注意哪些要点,有哪…...
Spring Security实战(一)——基于内存和数据库模型的认证与授权
目录 简介 一、初识Spring Security(入门案例) (1)新建project (2)选择依赖 (3)编写一个 HelloController (4)启动项目,访问localhost:8080…...

轻松掌握FFmpeg编程:从架构到实践
轻松掌握FFmpeg编程:从架构到实践 (Master FFmpeg Programming with Ease: From Architecture to Practice 引言 (Introduction)FFmpeg简介与应用场景 (Brief Introduction and Application Scenarios of FFmpeg)为什么选择FFmpeg进行音视频处理 (Why Choose FFmpeg…...
)
桌面应用程序开发攻略(初步了解)
什么是桌面应用程序? 桌面应用开发是指为桌面计算机或其他类似设备(如服务器)开发软件应用程序的过程。桌面应用通常是独立于浏览器运行的,并且可以在操作系统的桌面或应用程序菜单中找到。桌面应用可以使用各种编程语言开发&…...
【李老师云计算】HBase+Zookeeper部署及Maven访问(HBase集群实验)
索引 前言1. Zookeeper1.1 主机下载Zookeeper安装包1.2 主机解压Zookeeper1.3 ★解决解压后文件缺失1.4 主机配置Zookeeper文件1.4.1 配置zoo_sample.cfg文件1.4.2 配置/data/myid文件 1.5 主机传输Zookeeper文件到从机1.6 从机修改Zookeeper文件1.6.1 修改zoo.cfg文件1.6.2 修…...
第11章_常用类和基础API
第11章_常用类和基础API 讲师:尚硅谷-宋红康(江湖人称:康师傅) 官网:http://www.atguigu.com 本章专题与脉络 1. 字符串相关类之不可变字符序列:String 1.1 String的特性 java.lang.String 类代表字符串…...
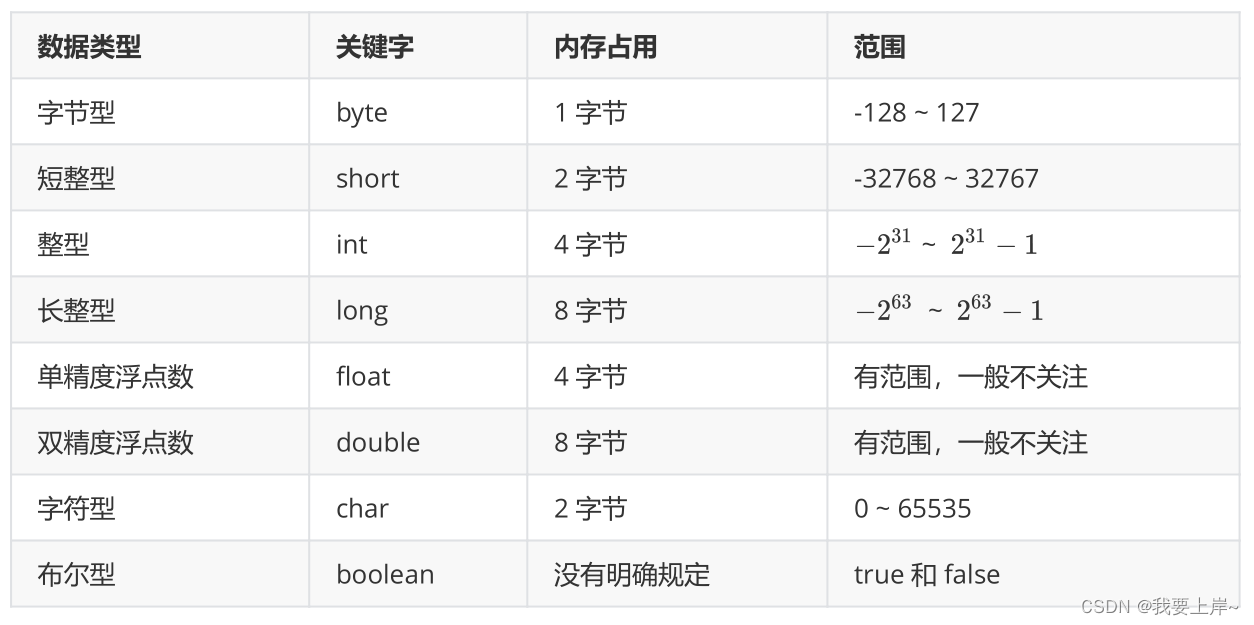
Java语言数据类型与c语言数据类型的不同
目录 一、c语言数据类型 1.基本类型: 2.枚举类型: 3.空类型: 4.派生类型: 二、C语言编程需要注意的64位和32机器的区别 三、 不同之处 一、c语言数据类型 首先,先来整体介绍一下C语言的数据类型分类。 1.基…...

Understanding the von Mises-Fisher Distribution: A Deep Dive into Spherical Data Modeling
1. 从指南针到星球大战:为什么我们需要冯米塞斯-费舍尔分布? 想象一下,你正在玩一个虚拟现实游戏,你的任务是控制一个飞行器在太空中航行。飞行器的方向,也就是它朝向哪里,可以用一个从球心指向球面的单位向…...

5倍效率提升:BiliTools AI视频总结如何重构你的内容消费方式
5倍效率提升:BiliTools AI视频总结如何重构你的内容消费方式 【免费下载链接】BiliTools A cross-platform bilibili toolbox. 跨平台哔哩哔哩工具箱,支持视频、音乐、番剧、课程下载……持续更新 项目地址: https://gitcode.com/GitHub_Trending/bili…...

COMSOL裂缝地层的THM耦合,离散裂缝模型,随机复杂裂缝,适合地热能研究。 增强地热系统...
COMSOL裂缝地层的THM耦合,离散裂缝模型,随机复杂裂缝,适合地热能研究。 增强地热系统,热流固耦合的开采过程。地下几千米藏着巨大的热能宝藏,增强型地热系统(EGS)就像给地球做"心脏搭桥手术…...

用大白话解释Sub-Agents
用大白话解释 Sub-Agent 就是"被派出去干活的 Claude 分身"。最直白的比喻 想象你是一个包工头(主 Claude):你接到一个装修任务,但你不可能同时贴瓷砖、刷墙、装电路。 所以你派出三个工人去分别干这三件事:…...

DDS混搭开发实录:当FastDDS遇到OpenDDS时我们踩过的那些坑
DDS混搭开发实录:当FastDDS遇到OpenDDS时我们踩过的那些坑 最近在做一个异构系统的集成项目,需要把几个不同团队开发的模块捏合到一起。这几个模块底层用的数据分发服务(DDS)实现各不相同,有的是RTI Connext DDS&#…...

如何利用d3-interpolate打造React-Move高级动画:完整插值技术指南
如何利用d3-interpolate打造React-Move高级动画:完整插值技术指南 【免费下载链接】react-move React Move | Beautiful, data-driven animations for React 项目地址: https://gitcode.com/gh_mirrors/re/react-move React-Move是一个基于React的数据驱动动…...

LoRA Diffusion生态系统与最佳实践
LoRA Diffusion生态系统与最佳实践 【免费下载链接】lora Using Low-rank adaptation to quickly fine-tune diffusion models. 项目地址: https://gitcode.com/gh_mirrors/lora2/lora LoRA Diffusion项目与HuggingFace Diffusers库的深度集成为用户提供了无缝的模型微调…...

RAGs知识库质量自动化检查:7个关键指标确保AI问答准确性
RAGs知识库质量自动化检查:7个关键指标确保AI问答准确性 【免费下载链接】rags Build ChatGPT over your data, all with natural language 项目地址: https://gitcode.com/gh_mirrors/ra/rags 在构建基于RAG(检索增强生成)技术的AI问…...

从0到1开发图片预览插件:qlImageSize核心功能实现原理探秘
从0到1开发图片预览插件:qlImageSize核心功能实现原理探秘 【免费下载链接】qlImageSize QuickLook and Spotlight plugins to display the dimensions, size and DPI of an image in the title bar instead of the filename. Also preview some unsupported format…...

React-Bulma-Components高级用法:组件组合与自定义
React-Bulma-Components高级用法:组件组合与自定义 【免费下载链接】react-bulma-components React components for Bulma framework 项目地址: https://gitcode.com/gh_mirrors/re/react-bulma-components React-Bulma-Components是基于Bulma框架的React组件…...
