2023-04-17 算法面试中常见的树和递归问题
二叉树和递归
0 LeetCode297 二叉树的序列化和反序列化
序列化是将一个数据结构或者对象转换为连续的比特位的操作,进而可以将转换后的数据存储在一个文件或者内存中,同时也可以通过网络传输到另一个计算机环境,采取相反方式重构得到原数据。请设计一个算法来实现二叉树的序列化与反序列化。这里不限定你的序列 / 反序列化算法执行逻辑,你只需要保证一个二叉树可以被序列化为一个字符串并且将这个字符串反序列化为原始的树结构。示例: 你可以将以下二叉树:1/ \2 3/ \4 5序列化为 "[1,2,3,null,null,4,5]"
提示: 这与 LeetCode 目前使用的方式一致,详情请参阅 LeetCode 序列化二叉树的格式。你并非必须采取这种方式,你也可以采用其他的方法解决这个问题。说明: 不要使用类的成员 / 全局 / 静态变量来存储状态,你的序列化和反序列化算法应该是无状态的。
import java.util.Arrays;
import java.util.LinkedList;
import java.util.Queue;public class Codec {// Encodes a tree to a single string.public String serialize(TreeNode root) {if (root == null) {return "[]";}Queue<String> res = new LinkedList<>();Queue<TreeNode> queue = new LinkedList<>();queue.offer(root);res.offer(String.valueOf(root.val));while(!queue.isEmpty()) {TreeNode node = queue.poll();// 有左节点就插入左节点,没有就插入nullif (node.left != null) {queue.offer(node.left);res.offer(String.valueOf(node.left.val));} else {res.offer("null");}// 有右节点就插入右节点,没有就插入nullif (node.right != null) {queue.offer(node.right);res.offer(String.valueOf(node.right.val));} else {res.offer("null");}}StringBuilder sb = new StringBuilder();sb.append("[");while(!res.isEmpty()) {sb.append(res.poll());if (!res.isEmpty()) {sb.append(",");}}sb.append("]");return sb.toString();}// Decodes your encoded data to tree.public TreeNode deserialize(String data) {data = data.substring(1, data.length()-1);if (data.length() == 0) {return null;}Queue<String> ls = new LinkedList<>(Arrays.asList(data.split(",")));Queue<TreeNode> queue = new LinkedList<>();TreeNode root = null;while(!ls.isEmpty()) {String res = ls.poll();// 创建根节点if (root == null) {root = new TreeNode(Integer.parseInt(res));queue.offer(root);continue;}// 注意:ls的长度总是奇数的,所以除了根节点,其余节点创建时可以一次取两个ls中的元素TreeNode father = queue.poll();// 创建左节点if (!"null".equals(res)) {TreeNode curr = new TreeNode(Integer.parseInt(res));assert father != null;father.left = curr;queue.offer(curr);}// 创建右节点res = ls.poll();assert res != null;if (!"null".equals(res)) {TreeNode curr = new TreeNode(Integer.parseInt(res));assert father != null;father.right = curr;queue.offer(curr);}}return root;}
}
1 二叉树的天然递归结构
递归的组成部分
- 递归终止条件
- 递归过程(
也称递归具体逻辑)
Leetcode104.Maximum Depth of Binary Tree 求二叉树的最大深度
给定一个二叉树,找出其最大深度。二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。说明: 叶子节点是指没有子节点的节点。示例:
给定二叉树 [3,9,20,null,null,15,7]3/ \9 20/ \15 7
public int maxDepth(TreeNode root) {// 递归的退出条件if (root == null) {// 当前树的根节点为null,那么当前树的深度为0return 0;}// 递归计算左子树最大深度int lMax = maxDepth(root.left);// 递归计算右子树最大深度int rMax = maxDepth(root.right);// 找到左右子树深度较大地那个,加1是因为当前层在递归回退时也算一层return Math.max(lMax, rMax) + 1;
}
111.二叉树的最小深度
class Solution {public int minDepth(TreeNode root) {if(root == null){return 0;}if(root.left == null || root.right == null){return Math.max(minDepth(root.left), minDepth(root.right)) + 1;}return Math.min(minDepth(root.left), minDepth(root.right)) + 1;}
}
上面的代码中的max实际是考虑了左右子树为空的情况,是下面代码的简化:
lass Solution {public int minDepth(TreeNode root) {if (root == null)return 0;if (root.left == null && root.right == null)return 1;if (root.left != null && root.right == null)return minDepth(root.left) + 1;if (root.right != null && root.left == null)return minDepth(root.right) + 1;return Math.min(minDepth(root.left) , minDepth(root.right)) + 1;}
}
2 Leetcode226号问题:反转二叉树
输入:4/ \2 7/ \ / \
1 3 6 9
输出:4/ \7 2/ \ / \
9 6 3 1
/************************************************************ @Description : 反转二叉树* 输入:** 4* / \* 2 7* / \ / \* 1 3 6 9* 输出:** 4* / \* 7 2* / \ / \* 9 6 3 1** @author : 梁山广(Liang Shan Guang)* @date : 2019/8/22 07:55* @email : liangshanguang2@gmail.com***********************************************************/
package Chapter07BSTAndRecursion.InverseBinaryTree;class Solution {public TreeNode invertTree(TreeNode root) {if(root == null){return null;}// 不为空的最下面的一个节点,交换左右子树即可TreeNode right = invertTree(root.right);TreeNode left = invertTree(root.left);// 下面是交换的核心root.right = left;root.left = right;return root;}
}
类似的问题:100、101、222、110
100. 相同的树
class Solution {public boolean isSameTree(TreeNode p, TreeNode q) {if(p == null && q == null) {return true;}if(p == null || q == null) {return false;}if(p.val != q.val){// 当前节点不相等直接返回falsereturn false;}else {// 相等地话直接往下递归return isSameTree(p.left, q.left) && isSameTree(p.right, q.right);}}
}
101.对称二叉树
和上面的第100题思路是完全一致的
class Solution {public boolean isSymmetric(TreeNode root) {if(root == null) {return true;}return isSymmetric(root.left, root.right);}// 利用上一节判断两棵树是否是相同树的代码来判断两个树是否堆成private boolean isSymmetric(TreeNode p, TreeNode q) {if(p == null && q == null){return true;}if(p == null || q == null){return false;}if(p.val != q.val){return false;}return isSymmetric(p.left, q.right) && isSymmetric(p.right, q.left);}
}
222.完全二叉树的节点个数
题目也太简单了吧,还好意思说是中级
class Solution {public int countNodes(TreeNode root) {if(root == null){return 0;}return countNodes(root.left) + countNodes(root.right) + 1;}
}
110.平衡二叉树
// 递归解决,计算子树高度,-1表示子树已经不平衡了
class Solution {public boolean isBalanced(TreeNode root) {// 计算各个点的深度 ,-1代表不平衡了return calDepth(root) != -1;}// 计算子树高度,-1表示已经不平衡了private int calDepth(TreeNode node){if(node == null){return 0;}// 递归计算左子树最大深度int lMax = calDepth(node.left);// 递归计算右子树最大深度int rMax = calDepth(node.right);// 左右子树高度差大于1时当前子树的高度返回-1if(lMax >= 0 && rMax >= 0 && Math.abs(lMax - rMax) <= 1){return Math.max(lMax, rMax) + 1;}else {return -1;}}
}
3 注意递归的终止条件
LeetCode112.路径总和
给定一个二叉树和一个目标和,判断该树中是否存在根节点到叶子节点的路径,这条路径上所有节点值相加等于目标和。说明: 叶子节点是指没有子节点的节点。示例:
给定如下二叉树,以及目标和 sum = 22,5/ \4 8/ / \11 13 4/ \ \7 2 1
返回 true, 因为存在目标和为 22 的根节点到叶子节点的路径 5->4->11->2
class Solution {// 不要用sum == 0作为递归终止条件,容易因为一开始传入地就是0而因为异常public boolean hasPathSum(TreeNode root, int sum) {// 1.递归终止条件if (root == null) {return false;}if (root.left == null && root.right == null) {// 注意题目中有说路径终点必须是叶子节点return root.val == sum;}// 2.递归的具体逻辑// 总和减去当前节点的值,然后看当前节点是否存在子树的节点和等于前面的新sumif (hasPathSum(root.left, sum - root.val)) {return true;}if (hasPathSum(root.right, sum - root.val)) {return true;}// 两侧都没找到返回falsereturn false;}
}
404.左叶子之和
用一个布尔变量标记是不是左子树
class Solution {public int sumOfLeftLeaves(TreeNode root) {// 递归具体逻辑return sumOfLeftLeaves(root, false);}private int sumOfLeftLeaves(TreeNode node, boolean isLeft) {// 1.递归退出条件if (node == null) {return 0;}// 左右子树都为空表明是叶子节点if (node.left == null && node.right == null) {// 是左子节点才返回节点的值if (isLeft) {return node.val;} else {// 右子节点就返回0,不影响最终的和return 0;}}// 2.递归具体逻辑return sumOfLeftLeaves(node.left, true) + sumOfLeftLeaves(node.right, false);}
}
4 定义递归问题
257.二叉树的所有路径
给定一个二叉树,返回所有从根节点到叶子节点的路径。说明: 叶子节点是指没有子节点的节点。示例:输入:1/ \
2 3\5输出: ["1->2->5", "1->3"]解释: 所有根节点到叶子节点的路径为: 1->2->5, 1->3
class Solution {public List<String> binaryTreePaths(TreeNode root) {List<String> result = new ArrayList<>();if (root == null) {return result;}if (root.left == null && root.right == null) {result.add(String.valueOf(root.val));}// 获取并拼接左子树字符串List<String> listL = binaryTreePaths(root.left);for (int i = 0; i < listL.size(); i++) {result.add(root.val + "->" + listL.get(i));}// 获取并拼接右子树字符串List<String> listR = binaryTreePaths(root.right);for (int i = 0; i < listR.size(); i++) {result.add(root.val + "->" + listR.get(i));}return result;}
}
113.路径总和 II
/************************************************************ @Description : 113.路径总和* @author : 梁山广(Liang Shan Guang)* @date : 2020/1/22 10:59* @email : liangshanguang2@gmail.com***********************************************************/
package Chapter07BSTAndRecursion.LeetCode113路径总和2;import Chapter07BSTAndRecursion.BSTUtil;
import Chapter07BSTAndRecursion.TreeNode;import java.util.ArrayList;
import java.util.List;class Solution {public List<List<Integer>> pathSum(TreeNode root, int sum) {List<List<Integer>> pathList = new ArrayList<>();List<Integer> path = new ArrayList<>();pathSum(root, sum, path, pathList);return pathList;}public void pathSum(TreeNode node, int sum, List<Integer> path, List<List<Integer>> pathList) {if (node == null) {return;}// 当前节点path.add(node.val);// 左右子树都为空说明到了叶子节点,把当前路径加到路径列表中if (node.left == null && node.right == null) {if (node.val == sum) {// 必须从path中新建一个来存储当前路径,否则后续修改path会会影响pathList.add(new ArrayList<>(path));}}pathSum(node.left, sum - node.val, path, pathList);pathSum(node.right, sum - node.val, path, pathList);// 当前层的递归退出时要删除当前节点path.remove(path.size() - 1);}/*** [5,4,8,11,null,13,4,7,2,null,null,5,1]* 22* <p>* [-2,null,-3]* -5*/public static void main(String[] args) {Integer[] arr = {1, -2, -3, 1, 3, -2, null, -1};int sum = 2;TreeNode root = BSTUtil.convert(arr);System.out.println(new Solution().pathSum(root, sum));}
}
129.求根到叶子节点数字之和
和上面的113类似,而且还简单点,不用筛选路径了
class Solution {public int sumNumbers(TreeNode root) {List<List<Integer>> pathList = new ArrayList<>();List<Integer> path = new ArrayList<>();pathSum(root, path, pathList);int sum = 0;for (List<Integer> pathTmp : pathList) {int num = 0;for (Integer numSingle : pathTmp) {num = num * 10 + numSingle;}sum +=num;}return sum;}public void pathSum(TreeNode node, List<Integer> path, List<List<Integer>> pathList) {if (node == null) {return;}// 当前节点path.add(node.val);// 左右子树都为空说明到了叶子节点,把当前路径加到路径列表中if (node.left == null && node.right == null) {// 必须从path中新建一个来存储当前路径,否则后续修改path会会影响pathList.add(new ArrayList<>(path));}pathSum(node.left, path, pathList);pathSum(node.right, path, pathList);// 当前层的递归退出时要删除当前节点path.remove(path.size() - 1);}
}
5 稍微复杂的递归逻辑
437.Path Sum III
双层递归,首先先序递归遍历每个节点,再以每个节点作为起始点递归寻找满足条件的路径。
// 递归遍历每个节点,每个节点作为根节点进行一次113.Path Sum II的操作
class Solution {// 符合条件的路径总数int cnt = 0;public int pathSum(TreeNode root, int sum) {if(root == null){return cnt;}// Todo:对当前节点进行Path Sum IIpathSumII(root, sum);pathSum(root.left, sum);pathSum(root.right, sum);return cnt;}private void pathSumII(TreeNode node, int sum){if(node == null){return;}int newSum = sum - node.val;if(newSum == 0){cnt++;}pathSumII(node.left, newSum);pathSumII(node.right, newSum);}
}
6 二分搜索树的问题
235.二叉搜索树的最近公共祖先
class Solution {public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {if(root == null){return null;}// pq均在右子树if(p.val > root.val && q.val > root.val){return lowestCommonAncestor(root.right, p, q);}// pq均在左子树if(p.val < root.val && q.val < root.val){return lowestCommonAncestor(root.left, p, q);}// p和q在root的两侧,当前的root肯定是最近的父节点return root;}
}
98.验证二叉树是否是二分搜索树
class Solution {/*** 中序遍历以node作为根节点的二分搜索树*/private void inOrder(TreeNode node, List<Integer> list) {// 递归终止条件if (node == null) {// 遍历到null节点就返回上一层递归return;}// 递归组成逻辑// 2.遍历左子树inOrder(node.left, list);// 1.访问当前节点。需要存储时可以放到list中list.add(node.val);// 3.遍历右子树inOrder(node.right, list);}// 中序遍历的结果是有序地,则说明二叉树是一个二叉搜索树public boolean isValidBST(TreeNode root) {List<Integer> list = new ArrayList<>();inOrder(root, list);for(int i = 1; i < list.size(); i++){if(list.get(i) <= list.get(i - 1)){return false;}}return true;}
}
450.删除二叉搜索树中的节点
参考地Part2Basic/Chapter06BST/BST.java
class Solution {public TreeNode deleteNode(TreeNode root, int key) {return remove(root, key);}/*** 寻找以node作为跟节点的二分搜索树的最小节点** @param node 根节点*/private TreeNode minimum(TreeNode node) {if (node.left == null) {return node;}return minimum(node.left);}/*** 删除以node作为根节点的二分搜索树中的最小节点,并返回删除节点后的新的二分搜索树的根节点** @param node 根节点*/private TreeNode removeMin(TreeNode node) {// 递归终止条件if (node.left == null) {// 递归遍历到左子树为空,说明找到了最小节点node// node.right是否为空都可以正常返回给上一级的父节点来设置父节点的左节点直接指向当前节点的右子树TreeNode rightNode = node.right;node.right = null;return rightNode;}// 递归组成逻辑// 当左节点不是null时就正常往下递归,返回当前节点给上一层节点设置下自己的左节点node.left = removeMin(node.left);return node;}/*** 删除** @param node 二分搜索树的根节点* @param e 待删除节点的值* @return 要挂载到当前节点父节点的子树*/private TreeNode remove(TreeNode node, int e) {// 递归终止条件if (node == null) {return null;}// 递归组成逻辑// 还没找到就接着往下找if (e < node.val) {// 要找的值比当前节点小,向左递归node.left = remove(node.left, e);return node;} else if (e > node.val) {// 要找的值比当前节点大,向右递归node.right = remove(node.right, e);return node;} else {// node.e == e 找到相等的节点了,下面删除指定值的节点if (node.left == null) {TreeNode rightNode = node.right;// 释放引用node.right = null;// 左节点为空,把node的右子树挂接到node的父亲节点即可return rightNode;}if (node.right == null) {TreeNode leftNode = node.left;// 释放引用node.left = null;// 右节点为空,把node的左子树挂接到node的父亲节点即可return leftNode;}// node的左右子树都不为空,就找node的右子树的最小值来代替nodeTreeNode minimumRight = minimum(node.right);// 警告:下面两行代码一定不要颠倒,一定要先设置right再设置left,否则会出现迭代引用!因为下面那行改变了node.right的结构。参考问题:https://coding.imooc.com/learn/questiondetail/143936.html// 选出node右子树最小元素来代替node,那么右子树最小元素就要从原来位置删掉minimumRight.right = removeMin(node.right);// 替换当前节点node的左右子树minimumRight.left = node.left;// 释放node的引用node.left = node.right = null;// 返回给上一级来设置父节点return minimumRight;}}
}
108.将有序数组转换为二叉搜索树
class Solution {// 升序数组是中序遍历的结果,答案是层序遍历的结果public TreeNode sortedArrayToBST(int[] nums) {return buildTree(nums, 0, nums.length - 1);}// 左右等分建立左右子树,中间节点作为子树根节点,递归该过程private TreeNode buildTree(int[] nums, int l, int r){if(l > r){return null;}// 等效于mid = (l + r) / 2,下面的实现是为了防止整型溢出int mid = l + (r - l) /2;TreeNode root = new TreeNode(nums[mid]);root.left = buildTree(nums, l, mid - 1);root.right = buildTree(nums, mid + 1, r);return root;}
}
230.二叉搜索树中第K小的元素
class Solution {int i = 0;int kth = 0;int kthSmallestVal = 0;public int kthSmallest(TreeNode root, int k) {kth = k;inOrder(root);return kthSmallestVal;}// 中序遍历的结果是升序排列的,所以找到第k小的元素就是累计中序遍历到额递归层数private void inOrder(TreeNode node){if(node == null){return;}inOrder(node.left);i++;if(i == kth){kthSmallestVal = node.val;}inOrder(node.right);}
}
236. 二叉树的最近公共祖先
参考235号问题
/*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode(int x) { val = x; }* }*/
class Solution {public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {// LCA 问题if (root == null) {return root;}if (root == p || root == q) {return root;}TreeNode left = lowestCommonAncestor(root.left, p, q);TreeNode right = lowestCommonAncestor(root.right, p, q);if (left != null && right != null) {return root;} else if (left != null) {return left;} else if (right != null) {return right;}return null;}
}
相关文章:

2023-04-17 算法面试中常见的树和递归问题
二叉树和递归 0 LeetCode297 二叉树的序列化和反序列化 序列化是将一个数据结构或者对象转换为连续的比特位的操作,进而可以将转换后的数据存储在一个文件或者内存中,同时也可以通过网络传输到另一个计算机环境,采取相反方式重构得到原数据…...

3分钟通过日志定位bug,这个技能测试人必须会
♥ 前 言 软件开发中通过日志记录程序的运行情况是一个开发的好习惯,对于错误排查和系统运维都有很大帮助。 Python 标准库自带了强大的 logging 日志模块,在各种 python 模块中得到广泛应用。 一、简单使用 1. 入门小案例 import logging logging.ba…...
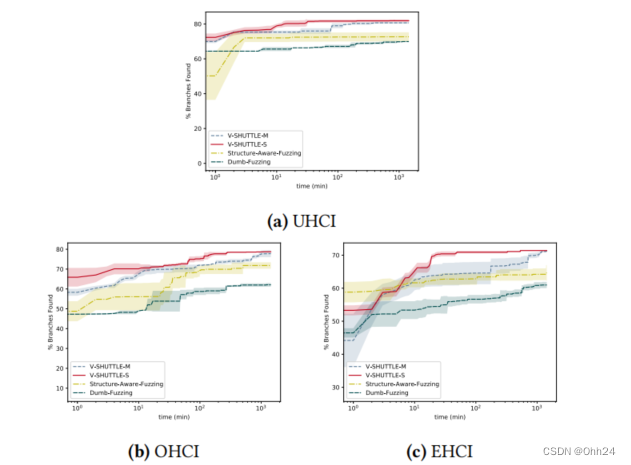
【论文总结】V-Shuttle:可扩展和语义感知的 Hypervisor 虚拟设备模糊测试
介绍 这是来自2021 CCS的一篇论文,作者有GaoningPan, Xingwei Lin, Xuhong Zhang, Yongkang Jia, Shouling Ji, Chunming Wu, Xinlei Ying, Jiashui Wang, Yanjun Wu。该论文提出V-shuttle的新框架来执行管控程序的模糊测试,该框架执行可扩展和语义感知…...

一篇文章让你搞懂TypeScript中的typeof()、keyof()是什么意思
TypeScript中的typeof()、keyof()是什么意思? 知识回调(不懂就看这儿!)场景复现核心干货👇👇👇举例引入字面量类型(literal types&…...
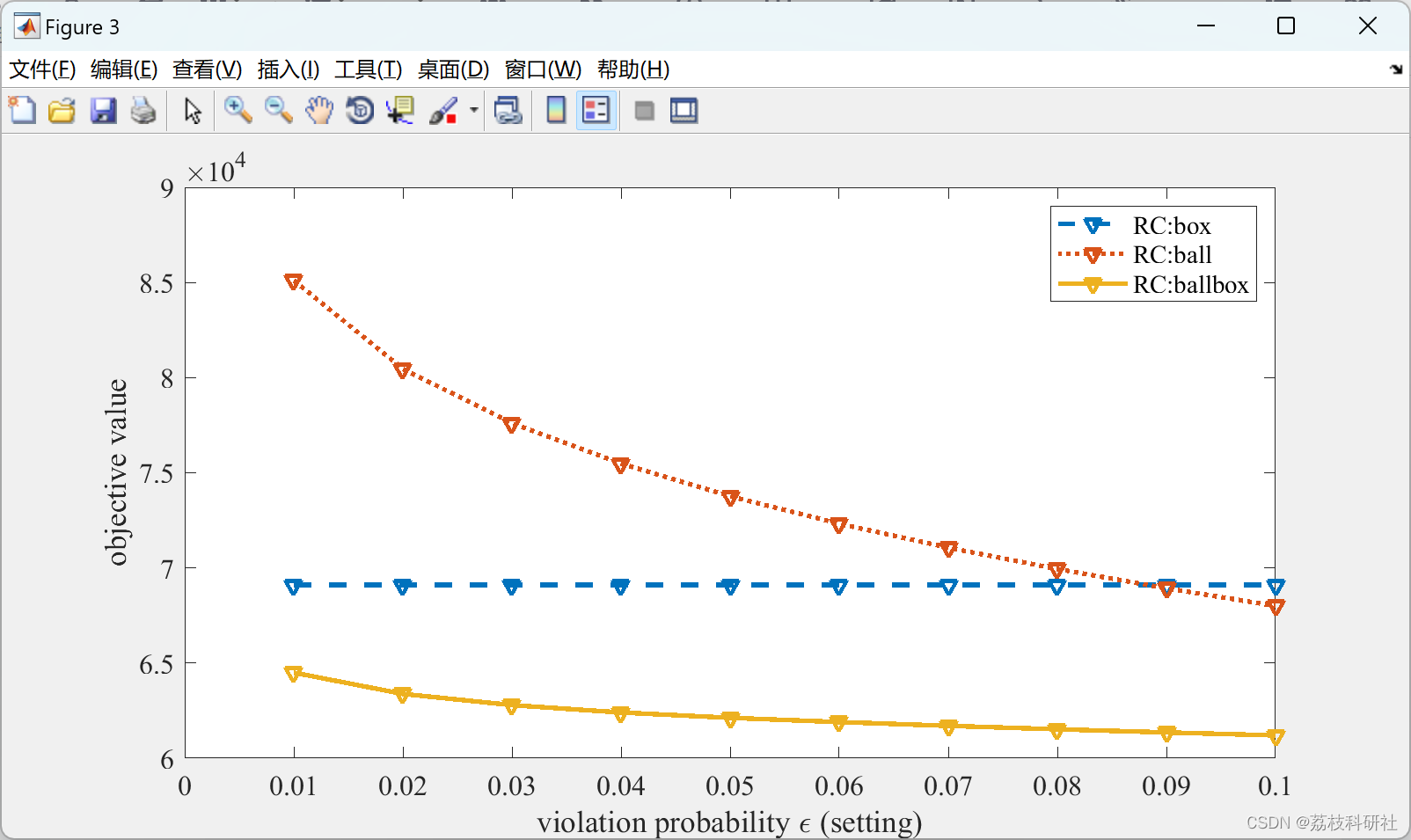
【机会约束、鲁棒优化】机会约束和鲁棒优化研究优化【ccDCOPF】研究(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...

4月想跳槽的同学,没有更好的选择,可以去美团
在美团干了半年,说一下自己的感受,美团是一家福利中等,工资待遇中上,高层管理团队强大,加班强度一般,技术不错,办公环境一般,工作氛围中上,部门差距之间工作体验差距巨大…...
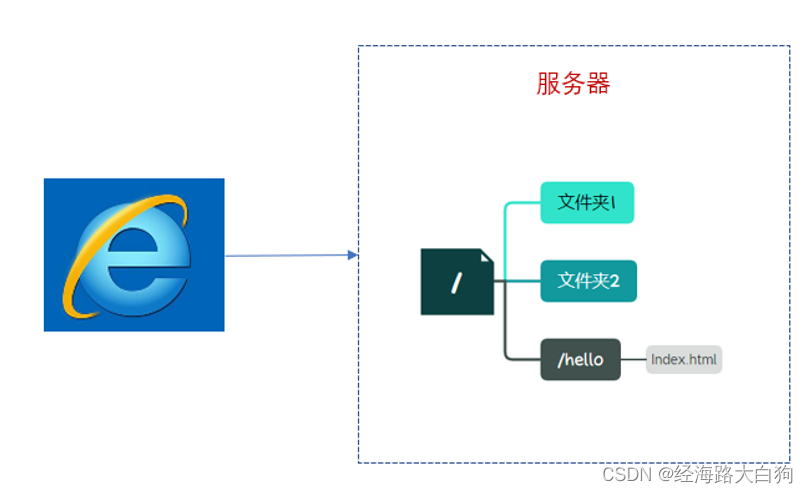
从输入url到页面展现(一)从浏览器解析url开始
前端面试有一道很考验人的问题,那就是:请你说一下从用户从输入url到页面展现的过程是怎样的?在接下来的一段时间呢,狗哥会从这一问题出发,开始剖析这个过程,希望可以让更多的小伙伴掌握到这个过程ÿ…...

购物 · 礼物
标题 前言必学场景词汇及用法书店花店玩具店讨价还价情境常用单词书店花店玩具店前言 加油 必学场景词汇及用法 书店 1.book store / book shop 书店 I browsed through the book store, but I didn’t find the book I was looking for. 我把书店里的书浏览了一番,但是没…...
)
可视化图表API格式要求有哪些?Sugar BI详细代码示例(2)
Sugar BI中的每个图表可以对应一个数据 API,用户浏览报表时,选定一定的过滤条件,点击「查询」按钮将会通过 API 拉取相应的数据;前面说过,为了确保用户数据的安全性,Sugar BI上的所有数据请求都在Sugar BI的…...
153. 寻找旋转排序数组中的最小值
已知一个长度为 n 的数组,预先按照升序排列,经由 1 到 n 次 旋转 后,得到输入数组。例如,原数组 nums [0,1,2,4,5,6,7] 在变化后可能得到: 若旋转 4 次,则可以得到 [4,5,6,7,0,1,2] 若旋转 7 次࿰…...
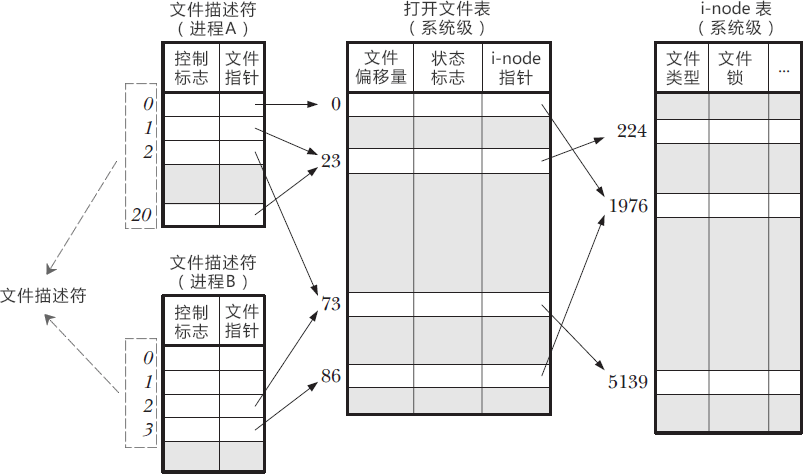
Linux 文件描述符
Linux 文件描述符 Linux 中一切皆文件,比如 C 源文件、视频文件、Shell脚本、可执行文件等,就连键盘、显示器、鼠标等硬件设备也都是文件。 一个 Linux 进程可以打开成百上千个文件,为了表示和区分已经打开的文件,Linux 会给每个…...

第17章_反射机制
第17章_反射机制 讲师:尚硅谷-宋红康(江湖人称:康师傅) 官网:http://www.atguigu.com 本章专题与脉络 1. 反射(Reflection)的概念 1.1 反射的出现背景 Java程序中,所有的对象都有两种类型:编…...

使用VBA小程序提高资产清查效率
资产清查是一件相当烦人的工作,去年使用LayUIPHPMS SQL Server 2014写了一个资产清查的程序,可惜写完了,LayUI已经停止更新了,就没有再完善下去,数据也没有更新,等于就废了。 今年又要进行资产清查…...

JavaSE学习进阶day07_02 异常
第三章 异常 3.1 异常概念 异常,就是不正常的意思。在生活中:医生说,你的身体某个部位有异常,该部位和正常相比有点不同,该部位的功能将受影响.在程序中的意思就是: 异常 :指的是程序在执行过程中,出现的非正常的情况࿰…...
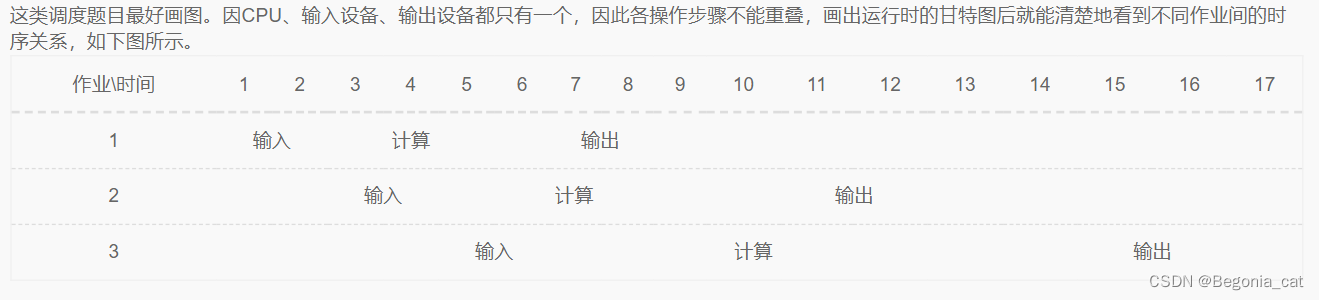
操作系统学习笔记
文章目录 操作系统虚拟内存锁缓存机制CPU性能指标进程、线程文件管理系统 操作系统 操作系统是控制应用程序的执行,并充当应用程序和计算机硬件之间的接口。在计算机系统中,处于最外层的是(应用软件) 。 面向用户的就是外层的&am…...

【Spring Boot】SpringBoot设计了哪些可拓展的机制?
文章目录 前言SpringBoot核心源码拓展Initializer拓展监听器ApplicationListenerBeanFactory的后置处理器 & Bean的后置处理器AOP其他的拓展点 前言 当我们引入注册中心的依赖,比如nacos的时候,当我们启动springboot,这个服务就会根据配置…...

《程序员面试金典(第6版)》面试题 10.10. 数字流的秩
题目描述 假设你正在读取一串整数。每隔一段时间,你希望能找出数字 x 的秩(小于或等于 x 的值的个数)。请实现数据结构和算法来支持这些操作,也就是说: 实现 track(int x) 方法,每读入一个数字都会调用该方法; 实现 g…...

智能洗地机好用吗?值得入手的洗地机推荐
洗地机是一款高效的地面清洁设备,不仅可以很好清理地面不同形态的干湿垃圾,还减少了人工和水资源的浪费,是我们日常生活中必不可少的清洁工具。作为以一位评测博主,很多朋友咨询我在选购洗地机时应该注意哪些要点,有哪…...
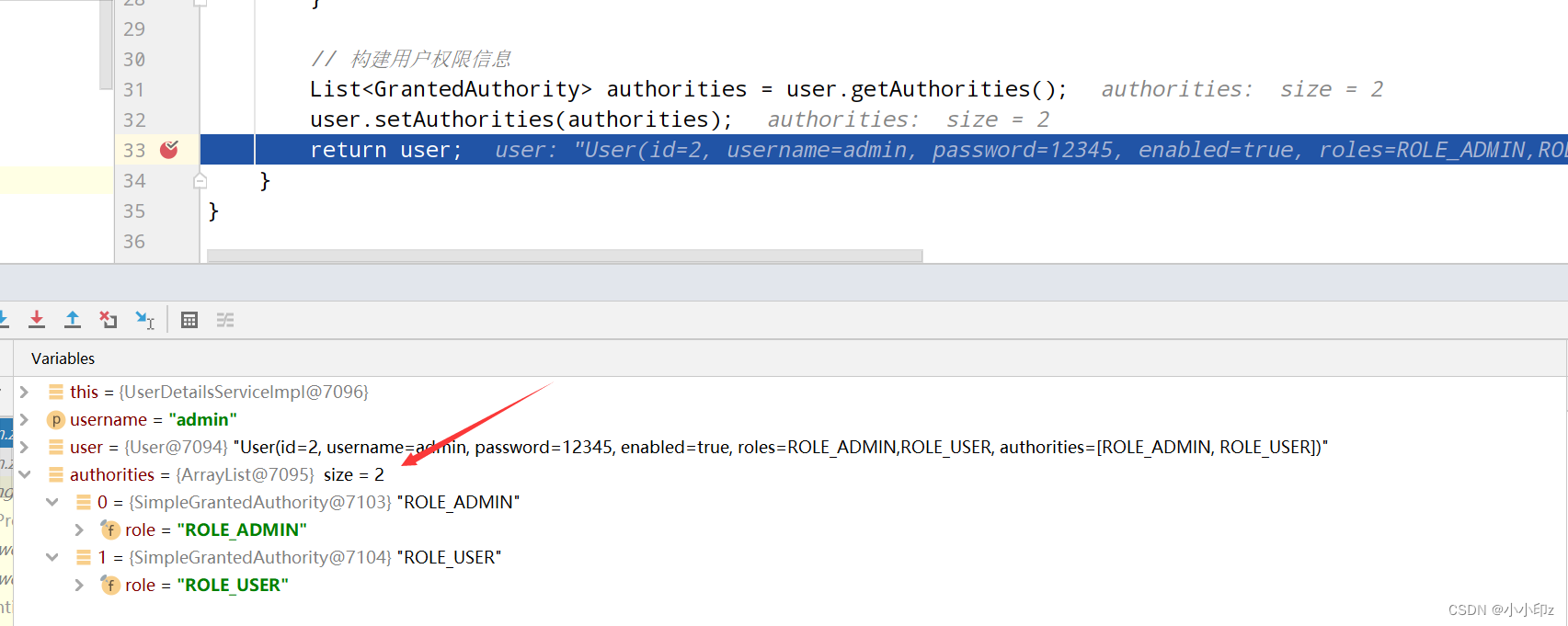
Spring Security实战(一)——基于内存和数据库模型的认证与授权
目录 简介 一、初识Spring Security(入门案例) (1)新建project (2)选择依赖 (3)编写一个 HelloController (4)启动项目,访问localhost:8080…...

轻松掌握FFmpeg编程:从架构到实践
轻松掌握FFmpeg编程:从架构到实践 (Master FFmpeg Programming with Ease: From Architecture to Practice 引言 (Introduction)FFmpeg简介与应用场景 (Brief Introduction and Application Scenarios of FFmpeg)为什么选择FFmpeg进行音视频处理 (Why Choose FFmpeg…...

【kafka】Golang实现分布式Masscan任务调度系统
要求: 输出两个程序,一个命令行程序(命令行参数用flag)和一个服务端程序。 命令行程序支持通过命令行参数配置下发IP或IP段、端口、扫描带宽,然后将消息推送到kafka里面。 服务端程序: 从kafka消费者接收…...

React hook之useRef
React useRef 详解 useRef 是 React 提供的一个 Hook,用于在函数组件中创建可变的引用对象。它在 React 开发中有多种重要用途,下面我将全面详细地介绍它的特性和用法。 基本概念 1. 创建 ref const refContainer useRef(initialValue);initialValu…...

基于uniapp+WebSocket实现聊天对话、消息监听、消息推送、聊天室等功能,多端兼容
基于 UniApp + WebSocket实现多端兼容的实时通讯系统,涵盖WebSocket连接建立、消息收发机制、多端兼容性配置、消息实时监听等功能,适配微信小程序、H5、Android、iOS等终端 目录 技术选型分析WebSocket协议优势UniApp跨平台特性WebSocket 基础实现连接管理消息收发连接…...

使用分级同态加密防御梯度泄漏
抽象 联邦学习 (FL) 支持跨分布式客户端进行协作模型训练,而无需共享原始数据,这使其成为在互联和自动驾驶汽车 (CAV) 等领域保护隐私的机器学习的一种很有前途的方法。然而,最近的研究表明&…...

聊聊 Pulsar:Producer 源码解析
一、前言 Apache Pulsar 是一个企业级的开源分布式消息传递平台,以其高性能、可扩展性和存储计算分离架构在消息队列和流处理领域独树一帜。在 Pulsar 的核心架构中,Producer(生产者) 是连接客户端应用与消息队列的第一步。生产者…...

YSYX学习记录(八)
C语言,练习0: 先创建一个文件夹,我用的是物理机: 安装build-essential 练习1: 我注释掉了 #include <stdio.h> 出现下面错误 在你的文本编辑器中打开ex1文件,随机修改或删除一部分,之后…...

Qwen3-Embedding-0.6B深度解析:多语言语义检索的轻量级利器
第一章 引言:语义表示的新时代挑战与Qwen3的破局之路 1.1 文本嵌入的核心价值与技术演进 在人工智能领域,文本嵌入技术如同连接自然语言与机器理解的“神经突触”——它将人类语言转化为计算机可计算的语义向量,支撑着搜索引擎、推荐系统、…...

Linux云原生安全:零信任架构与机密计算
Linux云原生安全:零信任架构与机密计算 构建坚不可摧的云原生防御体系 引言:云原生安全的范式革命 随着云原生技术的普及,安全边界正在从传统的网络边界向工作负载内部转移。Gartner预测,到2025年,零信任架构将成为超…...

sqlserver 根据指定字符 解析拼接字符串
DECLARE LotNo NVARCHAR(50)A,B,C DECLARE xml XML ( SELECT <x> REPLACE(LotNo, ,, </x><x>) </x> ) DECLARE ErrorCode NVARCHAR(50) -- 提取 XML 中的值 SELECT value x.value(., VARCHAR(MAX))…...

C# 类和继承(抽象类)
抽象类 抽象类是指设计为被继承的类。抽象类只能被用作其他类的基类。 不能创建抽象类的实例。抽象类使用abstract修饰符声明。 抽象类可以包含抽象成员或普通的非抽象成员。抽象类的成员可以是抽象成员和普通带 实现的成员的任意组合。抽象类自己可以派生自另一个抽象类。例…...
