2023年第十三届MathorCup高校数学建模挑战赛|A题|量子计算机在信用评分卡组合优化中的应用
目录
题目详情
最终收入 = 贷款利息收入 - 坏账损失
赛题说明 1:流程简化及示例
赛题说明 2:QUBO 模型简介
赛题说明 3:赛题数据
问题
题目详情
在银行信用卡或相关的贷款等业务中,对客户授信之前,需要先通过各种审核规则对客户的信用等级进行评定,通过评定后的客户才能获得信用或贷款资格。规则审核过程实际是经过一重或者多重组合规则后对客户进行打分,这些规则就被称为信用评分卡,每个信用评分卡又有多种阈值设置(但且只有一个阈值生效),这就使得不同的信用评分卡在不同的阈值下,对应不同的通过率和坏账率,一般通过率越高,坏账率也会越高,反之,通过率越低,坏账率也越低。
对银行来说,通过率越高,通过贷款资格审核的客户数量就越多,相应的银行获得的利息收入就会越多,但高通过率一般对应着高坏账率,而坏账意味着资金的损失风险,因此银行最终的收入可以定义为:
最终收入 = 贷款利息收入 - 坏账损失
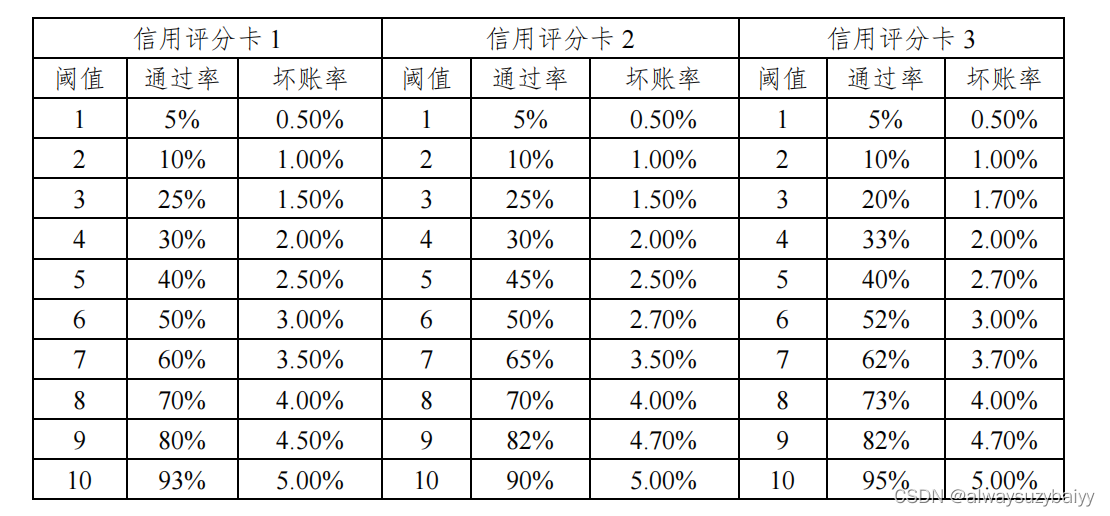
下表举例 3 个不同的信用评分卡,可以看到每种信用评分卡有 10 个阈值,每种阈值对应不同的坏账率和通过率:
赛题说明 1:流程简化及示例
我们将该问题进行做如下简化(本简化只适用本次比赛赛题,不能完全代表实际场景)。假设贷款资金为 1000000 元,银行贷款利息收入率为 8%,并以上面列举的三个信用评分卡作为选定的信用评分卡组合来测算银行最终收入。
由于每一信用评分卡有且只可选择 1 个阈值,假设信用评分卡 1 的阈值设置为 8,则通过表格可知,对应通过率为 70%,坏账率为 4.00%,信用评分卡 2 的阈值设置为 6,则通过率为 50%,坏账率为 2.70%,信用评分卡3 的阈值设置为 7,则通过率为 62%,坏账率为 3.70%。
总通过率为所有信用评分卡通过率相乘,即:
0.7×0.5×0.62 = 0.217
总坏账率为三种信用评分卡对应坏账率的平均值,即:
1/3×(0.04+0.027+0.037) = 0.0367
本次贷款利息收入为:贷款资金×利息收入率×总通过率×(1-总坏账率),即:
1000000×0.08×(0.7×0.5×0.62) ×(1-1/3×(0.04+0.027+0.037)) = 16758.18(元)
由坏账带来的坏账损失为:贷款资金×总通过率×总坏账率,即:
1000000×(0.7×0.5×0.62) ×(1/3×(0.04+0.027+0.037))=7522.666(元)
那么银行的最终收入为:贷款利息收入-坏账损失,即:
6758.18-7522.666 = 9235.514 (元)
选择不同的信用评分卡,不同的阈值组合,会给银行带来不同的收入与损失,由此决定银行最终收入。因此,银行的目标是选择最合理的信用评分卡组合以及其阈值,使得银行最终收入最多。
赛题说明 2:QUBO 模型简介
QUBO 模型是指二次无约束二值优化(Quadratic Unconstrained Binary Optimization)模型,它是一种用于解决组合优化问题的数学模型。在QUBO模型中,需要将问题转化为一个决策变量为二值变量,目标函数是一个二次函数形式优化模型。
QUBO 模型可以运行在量子计算机硬件上,通过量子计算机进行毫秒级的加速求解。这种模型和加速方式在未来各行业中将得到广泛的实际应用。因此现阶段研究基于 QUBO 模型的量子专用算法十分有应用价值。例如典型的图着色、旅行商问题、车辆路径优化问题等,都可以转化为 QUBO模型并借助于量子计算机求解。
赛题说明 3:赛题数据
附件 1 中共包含 100 张信用评分卡,每张卡可设置 10 种阈值之一,并对应各自的通过率与坏账率共 200 列,其中 t_1 代表信用评分卡 1 的通过率共 10 项,h_1 代表信用评分卡 1 的坏账率共 10 项,依次类推 t_100 代表信用评分卡 100 的通过率,h_100 代表信用评分卡 100 的坏率。
问题

相关文章:

2023年第十三届MathorCup高校数学建模挑战赛|A题|量子计算机在信用评分卡组合优化中的应用
目录 题目详情 最终收入 贷款利息收入 - 坏账损失 赛题说明 1:流程简化及示例 赛题说明 2:QUBO 模型简介 赛题说明 3:赛题数据 问题 题目详情 在银行信用卡或相关的贷款等业务中,对客户授信之前,需…...
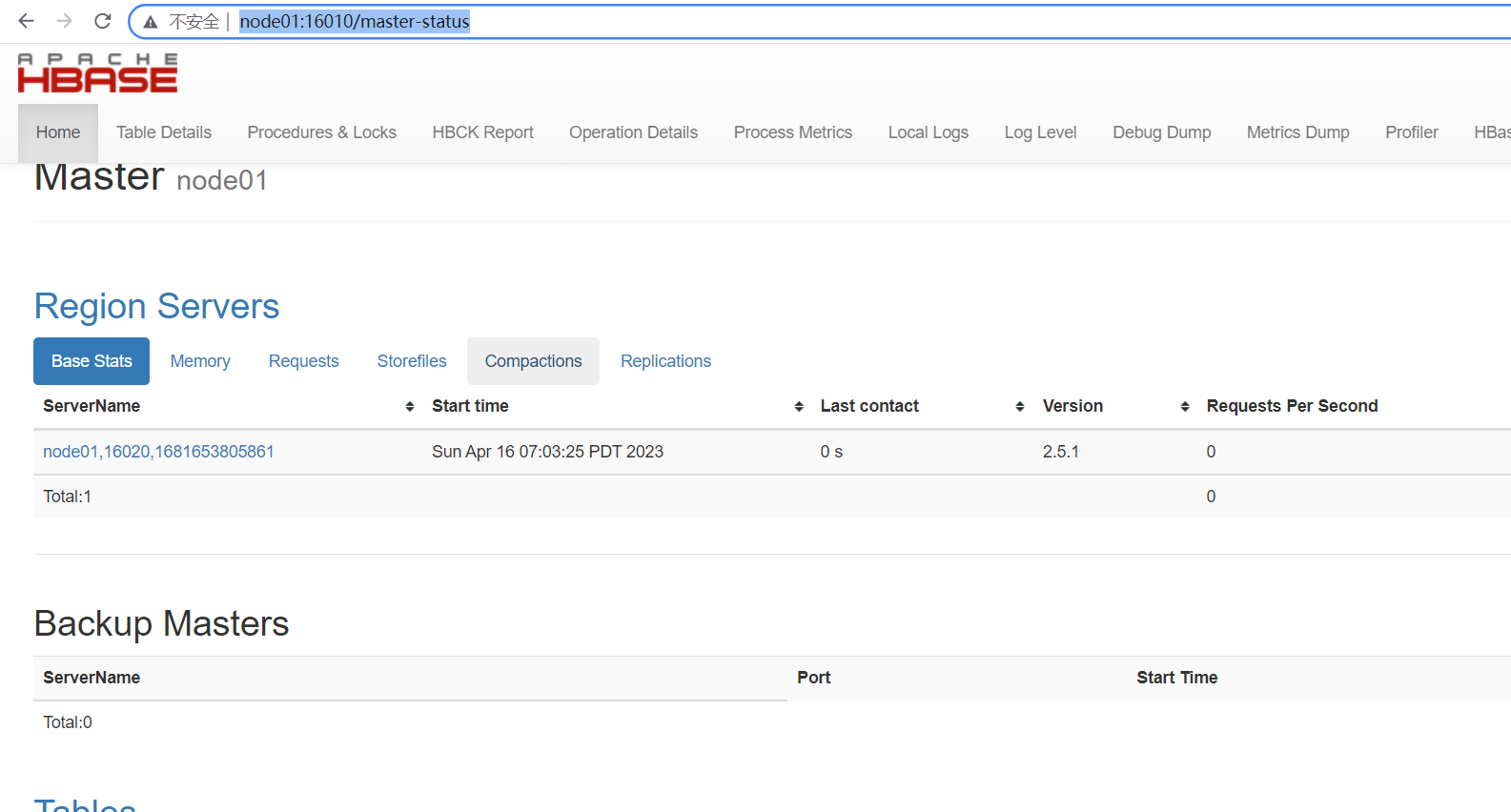
linux下搭建Hbase分布式数据库
文章目录 Hbase概念1.安装Hbase1.jdk的配置2.安装hbase 2.启动和操作1.启动服务2 **web-ui访问地址:http://node01:16010/master-status** 3.简单的操作1.连接 HBase2.帮助命令3.创建一张表 create a table4.使用查看表是否存在5.describe 查看表描述6.put命令插入数据到表7. s…...

unity,射手游戏
文章目录 介绍一,制作玩家具体函数脚本PlayerCharacter三、 制作玩家控制脚本 PlayerController,调用上面的函数方法四、 制作子弹脚本 shell五、 给玩家挂载脚本六、 制作坦克脚本七、 给坦克添加组件八、 开始游戏,播放动画九、 下载 介绍 …...

摒弃单一变现手段,开拓多元商业模式,破解场景单一APP盈利难题!
工具类APP已成为人们生活、工作中不可或缺的一部分,包括天气服务、搜索、日历等细分领域,在用户中存在巨大的市场需求。但是,这类APP也面临着一些难以避免的问题。 比如功能单一、用户停留时间较短、可替代性强等,这些问题会影响…...
JavaEE-轻松了解网络原理之TCP协议
目录 TCP协议TCP协议数据格式TCP原理确认应答超时重传连接管理三次握手四次挥手 滑动窗口流量控制拥塞控制延迟应答捎带应答面向字节流异常问题 TCP协议 TCP,即Transmission Control Protocol,传输控制协议. TCP协议数据格式 16位源端口号与16位目的端…...

薪资17K是一个怎样的水平?来看看98年测试工程师的面试全过程…
我的情况 大概介绍一下个人情况,男,本科,三年多测试工作经验,懂python,会写脚本,会selenium,会性能,然而到今天都没有收到一份offer!从年后就开始准备简历,年…...

OpenCV3 和 Qt5 计算机视觉:11~12
原文:Computer Vision with OpenCV 3 and Qt5 协议:CC BY-NC-SA 4.0 译者:飞龙 本文来自【ApacheCN 计算机视觉 译文集】,采用译后编辑(MTPE)流程来尽可能提升效率。 当别人说你没有底线的时候,…...

R包编写流程
文章目录 所需工具Step 1: 创建R项目Step 2: 在R文件夹中添加函数Step 3: 编辑元数据Step 4: 文档化Step 5: 检查包Step 6: 打包重要参考: 所需工具 R包的编写需要的工具包有:devtools,Rtools Step 1: 创建R项目 devtools::create_package…...

试验GPT写文章书
试验GPT写文章书 写一本名叫《寻找人生目标的十种方法》 回答 2023/4/22 16:12:31 很高兴为您提供以下内容,这是一本关于寻找人生目标的十种方法的建议和思考。 《寻找人生目标的十种方法》 第一章:明确自己的价值观 了解自己内心真正想要追求的东…...

class与typename的异同
一、class与typename的相同点 typename关键字常用于函数模板,这里首先引入函数模板的概念:函数模板代表了一个函数家族,该函数模板与类型无关,在使用时被参数化,根据实参类型产生函数的特定 类型版本 //函数模板格式…...
OpenCV 图像处理学习手册:6~7
原文:Learning Image Processing with OpenCV 协议:CC BY-NC-SA 4.0 译者:飞龙 本文来自【ApacheCN 计算机视觉 译文集】,采用译后编辑(MTPE)流程来尽可能提升效率。 当别人说你没有底线的时候,…...
)
Java中的序列化与反序列化(一)
1、概述 大家好,我是欧阳方超。今天来看一下Java序列化与反序列化的问题。 2、序列化与反序列化 2.1、序列化与反序列化的概念 在Java中,序列化是将对象转换为可存储或传输的格式(一般为字节流)的过程,序列化后的字…...

3.函数、结构体、包
一、函数定义和调用 package mainimport ("fmt" )func test() {fmt.Println("hello world") } func main() {test() }二、函数的参数 1.单个参数 func test(n int) {fmt.Println("传递进来的参数是", n) } func main() {test(10) }2.多个参数…...

科普丨关于 A/B 测试的十问十答
你想知道的,都在这里!本文是神策数据「十问十答」科普系列文章的第二期,围绕 A/B 测试展开。 1 Q:什么是 A/B 测试? A:A/B 测试作为互联网企业的核心增长手段之一,其价值已在实际应用中被多次验…...

尚融宝——整合OpenFeign与Sentinel实现兜底方法——验证手机号码是否注册功能
一、整合过程 在项目添加依赖:添加位置 <!--服务调用--><dependency><groupId>org.springframework.cloud</groupId><artifactId>spring-cloud-starter-openfeign</artifactId></dependency> 在需要的服务中添加启动注…...
几种常见的激活函数
文章目录 常见的激活函数介绍Sigmoid函数ReLU函数LeakyReLU函数Tanh函数Softmax函数总结 常见的激活函数介绍 激活函数是神经网络中的重要组成部分,它决定了神经元的输出。在神经网络的前向传播中,输入数据被传递给神经元,经过加权和和激活函…...

MySQL-数据库,数据表的基本操作
数据库,数据表的基本操作 1 数据库的基本操作1.1 创建数据库1.2 删除数据库 2 数据表的基本操作2.1 创建数据表2.1.1 主键约束2.1.2 外键约束2.1.3 非空约束2.1.4 唯一性约束2.1.5 默认约束2.1.6 自增列 2.2 查看数据表结构2.2.1 查看表基本结构语句DESC2.2.2 查看表…...

IC-14W网络IC卡读写器_银河麒麟桌面操作系统V10适配测试报告
银河麒麟操作系统产品NeoCertify 认证测试报告 系统版本:银河麒麟桌面操作系统V10 厂商名称: 广州荣士电子有限公司 认证产品:IC-14W网络IC卡读写器 测试日期: 2022-11-04 …...

面试常见问题
1.自我介绍 面试官您好,我叫**,在招聘网站上看到了公司的介绍和岗位要求,觉得非常有吸引力,结合自己的过往经历,也感觉自己能够胜任,所以很高兴能有这次面试机会。 参与工作已经5年了,18年毕业于…...

matlab数据归一化与反归一化处理
假如数据实际取值范围为 X i ∈ [ − π π ] , i 1 , 2 , 3 X_i \in [-\pi \ \ \pi], i1,2,3 Xi∈[−π π],i1,2,3,变量服从正态分布 示例如下: %% 数据归一化处理及其概率密度函数 clear clc Mu [0 0 0]; % 均值 Sigma [1 1 1]; % 标准差 C…...

IDEA运行Tomcat出现乱码问题解决汇总
最近正值期末周,有很多同学在写期末Java web作业时,运行tomcat出现乱码问题,经过多次解决与研究,我做了如下整理: 原因: IDEA本身编码与tomcat的编码与Windows编码不同导致,Windows 系统控制台…...

Vim 调用外部命令学习笔记
Vim 外部命令集成完全指南 文章目录 Vim 外部命令集成完全指南核心概念理解命令语法解析语法对比 常用外部命令详解文本排序与去重文本筛选与搜索高级 grep 搜索技巧文本替换与编辑字符处理高级文本处理编程语言处理其他实用命令 范围操作示例指定行范围处理复合命令示例 实用技…...

Appium+python自动化(十六)- ADB命令
简介 Android 调试桥(adb)是多种用途的工具,该工具可以帮助你你管理设备或模拟器 的状态。 adb ( Android Debug Bridge)是一个通用命令行工具,其允许您与模拟器实例或连接的 Android 设备进行通信。它可为各种设备操作提供便利,如安装和调试…...

《Qt C++ 与 OpenCV:解锁视频播放程序设计的奥秘》
引言:探索视频播放程序设计之旅 在当今数字化时代,多媒体应用已渗透到我们生活的方方面面,从日常的视频娱乐到专业的视频监控、视频会议系统,视频播放程序作为多媒体应用的核心组成部分,扮演着至关重要的角色。无论是在个人电脑、移动设备还是智能电视等平台上,用户都期望…...

智能在线客服平台:数字化时代企业连接用户的 AI 中枢
随着互联网技术的飞速发展,消费者期望能够随时随地与企业进行交流。在线客服平台作为连接企业与客户的重要桥梁,不仅优化了客户体验,还提升了企业的服务效率和市场竞争力。本文将探讨在线客服平台的重要性、技术进展、实际应用,并…...

linux 错误码总结
1,错误码的概念与作用 在Linux系统中,错误码是系统调用或库函数在执行失败时返回的特定数值,用于指示具体的错误类型。这些错误码通过全局变量errno来存储和传递,errno由操作系统维护,保存最近一次发生的错误信息。值得注意的是,errno的值在每次系统调用或函数调用失败时…...

2021-03-15 iview一些问题
1.iview 在使用tree组件时,发现没有set类的方法,只有get,那么要改变tree值,只能遍历treeData,递归修改treeData的checked,发现无法更改,原因在于check模式下,子元素的勾选状态跟父节…...

Python爬虫(一):爬虫伪装
一、网站防爬机制概述 在当今互联网环境中,具有一定规模或盈利性质的网站几乎都实施了各种防爬措施。这些措施主要分为两大类: 身份验证机制:直接将未经授权的爬虫阻挡在外反爬技术体系:通过各种技术手段增加爬虫获取数据的难度…...

拉力测试cuda pytorch 把 4070显卡拉满
import torch import timedef stress_test_gpu(matrix_size16384, duration300):"""对GPU进行压力测试,通过持续的矩阵乘法来最大化GPU利用率参数:matrix_size: 矩阵维度大小,增大可提高计算复杂度duration: 测试持续时间(秒&…...

C# SqlSugar:依赖注入与仓储模式实践
C# SqlSugar:依赖注入与仓储模式实践 在 C# 的应用开发中,数据库操作是必不可少的环节。为了让数据访问层更加简洁、高效且易于维护,许多开发者会选择成熟的 ORM(对象关系映射)框架,SqlSugar 就是其中备受…...
