Python调用最小二乘法
文章目录
- numpy实现
- scipy封装
- 速度对比
所谓线性最小二乘法,可以理解为是解方程的延续,区别在于,当未知量远小于方程数的时候,将得到一个无解的问题。最小二乘法的实质,是保证误差最小的情况下对未知数进行赋值。
最小二乘法是非常经典的算法,而且这个名字我们在高中的时候就已经接触了,属于极其常用的算法。此前曾经写过线性最小二乘法的原理,并用Python实现:最小二乘法及其Python实现;以及scipy中非线性最小二乘法的调用方式:非线性最小二乘法;还有稀疏矩阵的最小二乘法:稀疏矩阵最小二乘法。
下面讲对numpy和scipy中实现的线性最小二乘法进行说明,并比较二者的速度。
numpy实现
numpy中便实现了最小二乘法,即lstsq(a,b)用于求解类似于a@x=b中的x,其中,a为 M × N M\times N M×N的矩阵;则当b为 M M M行的向量时,刚好相当于求解线性方程组。对于 A x = b Ax=b Ax=b这样的方程组,如果 A A A是满秩仿真,那么可以表示为 x = A − 1 b x=A^{-1}b x=A−1b,否则可以表示为 x = ( A T A ) − 1 A T b x=(A^{T}A)^{-1}A^{T}b x=(ATA)−1ATb。
当b为 M × K M\times K M×K的矩阵时,则对每一列,都会计算一组x。
其返回值共有4个,分别是拟合得到的x、拟合误差、矩阵a的秩、以及矩阵a的单值形式。
import numpy as np
np.random.seed(42)
M = np.random.rand(4,4)
x = np.arange(4)
y = M@x
xhat = np.linalg.lstsq(M,y)
print(xhat[0])
#[0. 1. 2. 3.]
scipy封装
scipy.linalg同样提供了最小二乘法函数,函数名同样是lstsq,其参数列表为
lstsq(a, b, cond=None, overwrite_a=False, overwrite_b=False, check_finite=True, lapack_driver=None)
其中a, b即 A x = b Ax=b Ax=b,二者均提供可覆写开关,设为True可以节省运行时间,此外,函数也支持有限性检查,这是linalg中许多函数都具备的选项。其返回值与numpy中的最小二乘函数相同。
cond为浮点型参数,表示奇异值阈值,当奇异值小于cond时将舍弃。
lapack_driver为字符串选项,表示选用何种LAPACK中的算法引擎,可选'gelsd', 'gelsy', 'gelss'。
import scipy.linalg as sl
xhat1 = sl.lstsq(M, y)
print(xhat1[0])
# [0. 1. 2. 3.]
速度对比
最后,对着两组最小二乘函数做一个速度上的对比
from timeit import timeit
N = 100
A = np.random.rand(N,N)
b = np.arange(N)timeit(lambda:np.linalg.lstsq(A, b), number=10)
# 0.015487500000745058
timeit(lambda:sl.lstsq(A, b), number=10)
# 0.011151800004881807
这一次,二者并没有拉开太大的差距,即使将矩阵维度放大到500,二者也是半斤八两。
N = 500
A = np.random.rand(N,N)
b = np.arange(N)timeit(lambda:np.linalg.lstsq(A, b), number=10)
0.389679799991427
timeit(lambda:sl.lstsq(A, b), number=10)
0.35642060000100173
相关文章:

Python调用最小二乘法
文章目录 numpy实现scipy封装速度对比 所谓线性最小二乘法,可以理解为是解方程的延续,区别在于,当未知量远小于方程数的时候,将得到一个无解的问题。最小二乘法的实质,是保证误差最小的情况下对未知数进行赋值。 最小…...

15.数据表格.上
本节课我们来开始了解 Layui 的内置模块:table 数据表格。 一.基本使用 1. table 模块,通过异步加载数据来渲染表格来展现数据内容; <table id"table"></table> layui.use([table], () > { const table …...

在poetry虚拟环境下打包exe
本博客介绍了在poetry虚拟环境下打包exe的流程,包含两个部分 打包的基本流程打包过程中遇到的问题 打包的基本流程 copy打包工具到本地,(share:\公用共享\芯片部\乔羽\img_generate\系统部提供的打包exe工具) 用poetry搭建虚拟环境 在打包…...
【Unity VR开发】结合VRTK4.0:高亮与标签
语录: 信仰到底是什么呢,就是纵身一跃,就是我们跟神之间一个永远的约定,是舍弃日的去开始新的生活;信仰就是从今以后,再也不要放开你的手。 前言: Interactable Highlighter :当我们的手柄触碰…...

有了MySQL,为什么还要有NoSQL
🏆今日学习目标: 🍀MySQL和NoSQL的区别 ✅创作者:林在闪闪发光 ⏰预计时间:30分钟 🎉个人主页:林在闪闪发光的个人主页 🍁林在闪闪发光的个人社区,欢迎你的加入: 林在闪闪…...
找PPT模板就上这5个网站~
分享几个可以永久免费下载PPT模板、素材的网站,上万个模板随便下载,赶紧收藏起来~ 1、菜鸟图库 https://www.sucai999.com/search/ppt/0_0_0_1.html?vNTYxMjky 网站素材非常全面,主要以设计类素材为主,办公类素材也很多&#x…...

Ae:摄像机选项
摄像机选项 Camera Options 快捷键:AA 摄像机选项 Camera Options与“摄像机设置”中的参数大同小异且同步变化,额外增加了一些与镜头模糊和散景光斑形状有关的摄像机属性。 请参阅: 《Ae:摄像机设置》 在合成设置中,选…...

嵌入式日志库ulog的使用和解析
嵌入式日志信息保存调试(ulog) 获取 项目地址:https://github.com/rdpoor/ulog uLog 为嵌入式微控制器或任何资源有限的系统提供结构化的日志记录机制。它继承了流行的 Log4c 和 Log4j 平台背后的一些概念,但开销更低。 使用方…...

自阿里P8爆出内部1031道java面试题后,在Boss直聘狂拿千份Offer
开始之前我问大家几个问题,看大家是如何思考的: 1.程序员一定要去一线城市漂泊吗?在自己家乡如何拿到一份满意的薪水? 2.程序员被裁员、找不到工作,代表什么? 3.程序员一定要进一线大厂吗?你…...
)
Java最新面试题100道,包含答案示例(41-50题)
非常抱歉,我理解有误。以下是第41至45题的Java面试题和答案: 请问Java中有哪些常用的集合类型? 答:Java中有多种常用的集合类型,包括List、Set、Map等。其中,List和Set分别代表一组元素的序列和一组无序不…...

C++之深入解析野指针和悬空指针
一、野指针 ① 什么是野指针? 野指针指向一个已删除的对象或未申请访问受限内存区域的指针。与空指针不同,野指针无法通过简单地判断是否为NULL避免,而只能通过养成良好的编程习惯来尽力减少,对野指针进行操作很容易造成程序错误…...

YOLOv7+单目测距(python)
YOLOv7单目测距(python) 1. 相关配置2. 测距原理3. 相机标定3.1:标定方法13.2:标定方法2 4. 相机测距4.1 测距添加4.2 主代码 5. 实验效果 相关链接 1. YOLOV5 单目测距(python) 2. YOLOV5 单目跟踪&…...
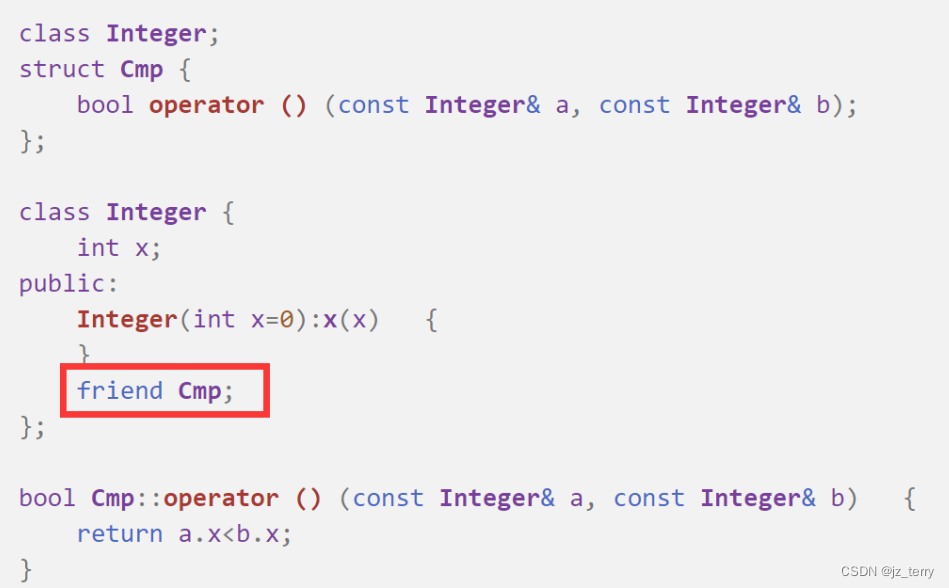
SYSU程设c++(第九周)函数对象、友元函数、友元类
函数对象: 如果一个类定义了operator()运算符函数,则可以使用该类的对象名为函数名调用这个函数. 函数对象是一个对象,但调用形式和普通函数调用一样,因此取名叫函数对象 (注意operator()先有个括号,接着才是括号(参数…...

Target品质审核零容忍问题点——上篇
【Target品质审核零容忍问题点——上篇】 Target品质验厂审核过程中共有110多个问题点,其中包含零容忍问题12项,审核当天如果出现任何零容忍项或出现很多扣分项,将直接影响最后的结果,极容易导致验厂不通过。建议工厂在遇到Target…...
使用node版本管理器gnvm
目录 一、官网 二、下载 三、查看本机node安装地址 四、将gnvm放到node安装目录 五、安装其他版本node(以管理员身份打开CMD) 六、使用指定版本(以管理员身份打开CMD) 七、查看当前版本(以管理员身份打开CMD&…...
SpringBoot中使用redis事务
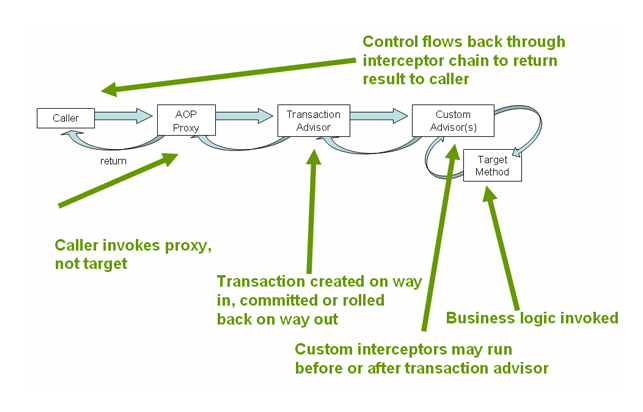
本文基于SpringBoot 2.X 事务在关系型数据库的开发中经常用到,其实非关系型数据库,比如redis也有对事务的支持,本文主要探讨在SpringBoot中如何使用redis事务。 事务的相关介绍可以参考: 0、起因 在一次线上事故中,我们…...

2023全网汇总PMP备考攻略(附答题技巧)
一,多复习和学习新版考纲 01《PMBOK》看三遍 这边建议看三遍《PMBOK》,更有利于我们巩固知识,查缺补漏。 第一遍 第一遍是老师带着我们去看。这个时候一定要非常专心,千万不要上课走神或者玩手机。因为这一遍老师会告诉我们&a…...

lightdb/pg reload guc 参数机制
lightdb/pg reload guc 参数机制 本文主要讲述调用pg_reload_conf 后,到guc被真正修改之间发送的故事。(基于pg13) pg_reload_conf 函数实现如下: Datum pg_reload_conf(PG_FUNCTION_ARGS) {if (kill(PostmasterPid, SIGHUP)){ereport(WARNING,(errms…...

E. Archaeology(纯思维)
Problem - E - Codeforces 爱丽丝买了一个刚果总理视频的订阅,正在看一部关于苏格兰卡特林湖的因子岛的考古发现的纪录片。考古学家发现了一本书,其年代和来源都不明。也许爱丽丝可以对它进行一些解释? 这本书包含一串字符 "a"、&…...
FISCO BCOS(三十四)———商品溯源(智能合约+后端)
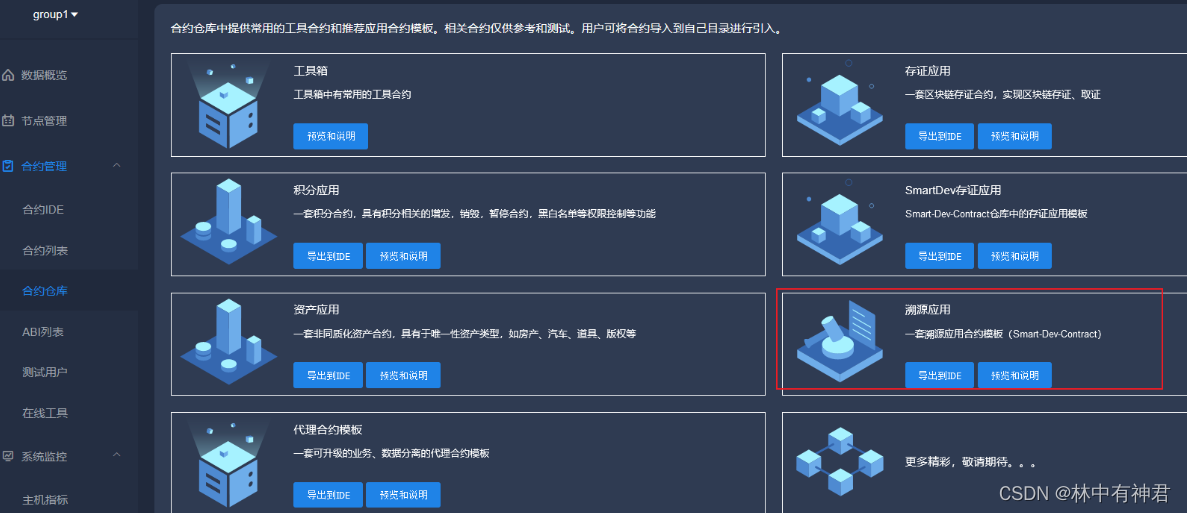
FISCO BCOS(三十四)———商品溯源(智能合约+后端) 一、智能合约函数调用流程 注:智能合约来源(官网的合约仓库中) 但是TraceabilityFactory合约有问题,我已经做了修改,可以看原版与我的,只有一个函数不同。 官网上这套合约在TraceabilityFactory这个合约上缺少getGo…...

零门槛NAS搭建:WinNAS如何让普通电脑秒变私有云?
一、核心优势:专为Windows用户设计的极简NAS WinNAS由深圳耘想存储科技开发,是一款收费低廉但功能全面的Windows NAS工具,主打“无学习成本部署” 。与其他NAS软件相比,其优势在于: 无需硬件改造:将任意W…...

大话软工笔记—需求分析概述
需求分析,就是要对需求调研收集到的资料信息逐个地进行拆分、研究,从大量的不确定“需求”中确定出哪些需求最终要转换为确定的“功能需求”。 需求分析的作用非常重要,后续设计的依据主要来自于需求分析的成果,包括: 项目的目的…...
)
云计算——弹性云计算器(ECS)
弹性云服务器:ECS 概述 云计算重构了ICT系统,云计算平台厂商推出使得厂家能够主要关注应用管理而非平台管理的云平台,包含如下主要概念。 ECS(Elastic Cloud Server):即弹性云服务器,是云计算…...

简易版抽奖活动的设计技术方案
1.前言 本技术方案旨在设计一套完整且可靠的抽奖活动逻辑,确保抽奖活动能够公平、公正、公开地进行,同时满足高并发访问、数据安全存储与高效处理等需求,为用户提供流畅的抽奖体验,助力业务顺利开展。本方案将涵盖抽奖活动的整体架构设计、核心流程逻辑、关键功能实现以及…...

HTML 列表、表格、表单
1 列表标签 作用:布局内容排列整齐的区域 列表分类:无序列表、有序列表、定义列表。 例如: 1.1 无序列表 标签:ul 嵌套 li,ul是无序列表,li是列表条目。 注意事项: ul 标签里面只能包裹 li…...

DIY|Mac 搭建 ESP-IDF 开发环境及编译小智 AI
前一阵子在百度 AI 开发者大会上,看到基于小智 AI DIY 玩具的演示,感觉有点意思,想着自己也来试试。 如果只是想烧录现成的固件,乐鑫官方除了提供了 Windows 版本的 Flash 下载工具 之外,还提供了基于网页版的 ESP LA…...

成都鼎讯硬核科技!雷达目标与干扰模拟器,以卓越性能制胜电磁频谱战
在现代战争中,电磁频谱已成为继陆、海、空、天之后的 “第五维战场”,雷达作为电磁频谱领域的关键装备,其干扰与抗干扰能力的较量,直接影响着战争的胜负走向。由成都鼎讯科技匠心打造的雷达目标与干扰模拟器,凭借数字射…...

排序算法总结(C++)
目录 一、稳定性二、排序算法选择、冒泡、插入排序归并排序随机快速排序堆排序基数排序计数排序 三、总结 一、稳定性 排序算法的稳定性是指:同样大小的样本 **(同样大小的数据)**在排序之后不会改变原始的相对次序。 稳定性对基础类型对象…...

LangChain知识库管理后端接口:数据库操作详解—— 构建本地知识库系统的基础《二》
这段 Python 代码是一个完整的 知识库数据库操作模块,用于对本地知识库系统中的知识库进行增删改查(CRUD)操作。它基于 SQLAlchemy ORM 框架 和一个自定义的装饰器 with_session 实现数据库会话管理。 📘 一、整体功能概述 该模块…...

【从零学习JVM|第三篇】类的生命周期(高频面试题)
前言: 在Java编程中,类的生命周期是指类从被加载到内存中开始,到被卸载出内存为止的整个过程。了解类的生命周期对于理解Java程序的运行机制以及性能优化非常重要。本文会深入探寻类的生命周期,让读者对此有深刻印象。 目录 …...
