Transformer中的注意力机制及代码
文章目录
- 1、简介
- 2、原理
- 2.1 什么是注意力机制
- 2.2 注意力机制在NLP中解决了什么问题
- 2.3 注意力机制公式解读
- 2.4 注意力机制计算过程
- 3、单头注意力机制与多头注意力机制
- 4、代码
- 4.1 代码1
- 4.2 代码2
1、简介
最近在学习transformer,首先学习了多头注意力机制,这里积累一下自己最近的学习内容。本文有大量参考内容,包括但不限于:
① 注意力,多注意力,自注意力及Pytorch实现
② Attention 机制超详细讲解(附代码)
③ Transformer 鲁老师机器学习笔记
④ transformer中: self-attention部分是否需要进行mask?
⑤ nn.Transformer Pytorch官方文档
⑥ The llustrated Transformer
⑦ 论文:Attention Is All You Need
⑧ attention-is-all-you-need-pytorch/transformer/SubLayers.py
⑨ Transformer、GPT、BERT,预训练语言模型的前世今生
2、原理
2.1 什么是注意力机制
重要性:Transformer、BETR等模型在NLP领域取得了重大突破,注意力机制(Attention Mechanism)起到了重要作用;注意力机制早在上世纪九十年代就有研究,2014年,Volodymyr在《Recurrent Models of Visual Attention》一文中将其应用在视觉领域,后来伴随着2017年Ashish Vaswani的《Attention is all you need》中Transformer结构的提出,注意力机制在NLP,CV相关问题的网络设计上被广泛应用。
"注意力机制"从名字中我们就可以看出关键在于注意力这个词,其实注意力在人身上能完美的体现,看下面这张狗的照片,大部分人的关注点儿都在狗和狗穿的衣服上,那么狗身后的背景往往被忽略,实际上注意力机制就是将人的注意力行为应用在机器上,让机器学会去感知数据中重要的和不重要的部分。还是以下图为例,进行狗识别的任务时,我们希望机器会更加关注重要部分(狗)而忽略不重要部分(背景)。

2.2 注意力机制在NLP中解决了什么问题
早期在解决机器翻译这一类序列到序列(Sequence to Sequence)的问题时,通常采用的做法是利用一个编码器(Encoder)和一个解码器(Decoder)构建端到端的神经网络模型,但是基于编码解码的神经网络存在两个问题,拿机器翻译举例:
问题1:如果翻译的句子很长很复杂,比如直接一篇文章输进去,模型的计算量很大,并且模型的准确率下降严重。
问题2:在翻译时,可能在不同的语境下,同一个词具有不同的含义,但是网络对这些词向量并没有区分度,无法结合词的上下文语境,导致翻译效果比较差。即无法解决词的多义(比如:”我在用苹果手机“和”这个苹果真好吃“这两个句子均出现苹果这个词,但是表达的意义完全不同)。
为了解决上述问题,注意力机制被提出。
2.3 注意力机制公式解读
我们首先以Transformer论文中的自注意力(Self-Attention)机制说起,Self-Attention的实现公式为:

这个公式中的Q、K和V分别代表Query、Key和Value,是三个矩阵。看到这里先不要着急,我们现在只需要知道自注意力机制中有这三个矩阵即可。
回顾一下向量点乘的几何意义:向量x在向量y方向上的投影再与向量y的乘积,能反映两个向量的相似度,且向量点乘的结果越大,两个向量越相似。
矩阵的每一行也可以看作是向量,如果一个矩阵 X 乘以其本身的转置 X T X^{\scriptscriptstyle T} XT,那么得到的结果不就能刻画该矩阵自身与自身的相似度吗?下面以词向量为例,这个矩阵中,每行为一个词的词向量。矩阵与自身的转置相乘,生成了目标矩阵,目标矩阵其实就是一个词的词向量与各个词的词向量的相似度。为了更清楚的表达,这里我引用鲁老师在transformer中的示例图片和代码:
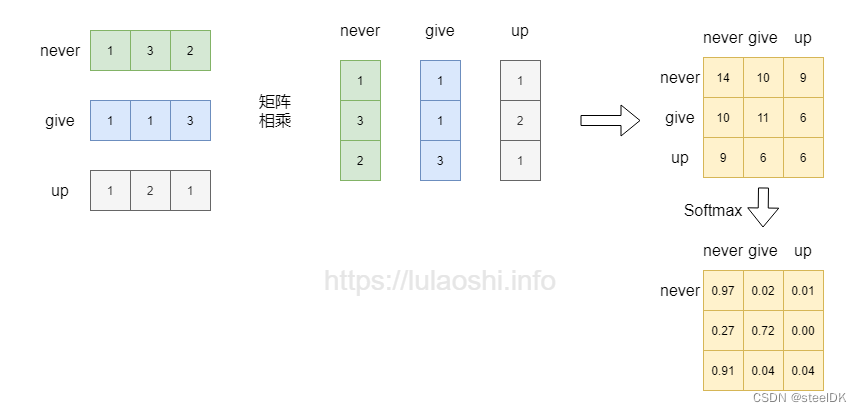
词向量相乘之后,如果再加上一个softmax,即softmax( X X T X^{T} XT)对向量相乘后的矩阵的每一行做归一化,那么就是对相似度的归一化,也就得到了一个归一化后的权重矩阵,这个矩阵中,数值越大代表相似度越大,比如never和never的相似度高达0.97。
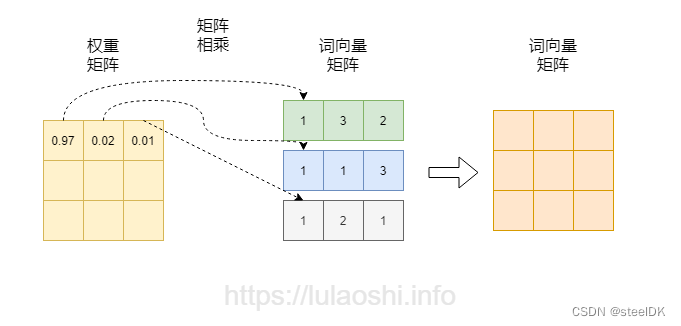
在图一的基础上,将softmax得到的权重矩阵与词向量相乘,如图二箭头所示。权重矩阵中某一行分别与词向量的一列相乘,词向量矩阵的一列其实代表着不同词的某一维度。经过这样一个矩阵相乘,相当于一个加权求和的过程,得到结果词向量是经过加权求和之后的新表示。
上述过程的Pytorch实现:
import torch
import torch.nn as nnx = torch.tensor([[1, 3, 2], [1, 1, 3], [1, 2, 1]], dtype=torch.float64)attention_scores = torch.matmul(x, x.transpose(-1, -2))
attention_scores = nn.functional.softmax(attention_scores, dim=-1)print(attention_scores)有关与torch.matmul()相关函数的用法,可以参考:Pytorch教程之torch.mm、torch.bmm、torch.matmul、masked_fill。
2.4 注意力机制计算过程
在2.3中我们对矩阵乘法代表相似度的过程进行了初步了解,因此这里我们首先介绍一下自注意力机制公式中的矩阵Q、K、V是如何得到的。Transformer论文中将这个Attention公式描述为:Scaled Dot-Product Attention。其中,Q为Query、K为Key、V为Value。在Transformer的Encoder中所使用的Q、K、V其实都是从同样的输入矩阵X线性变换而来的,可以简单理解为:
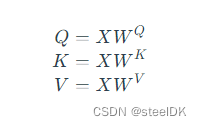
其中 W Q W^{Q} WQ、 W K W^{K} WK、 W V W^{V} WV是三个可训练的参数矩阵,输入矩阵X分别与 W Q W^{Q} WQ、 W K W^{K} WK、 W V W^{V} WV相乘,得到Q、K、V,相当于经过了一次线性变换。Attention不直接使用X,而是使用矩阵乘法生成这三个矩阵,这三个可训练的参数矩阵增强了模型的拟合能力。
Self-Attention计算过程如下:
第一步:X与W相乘,生成Q、K、V矩阵。
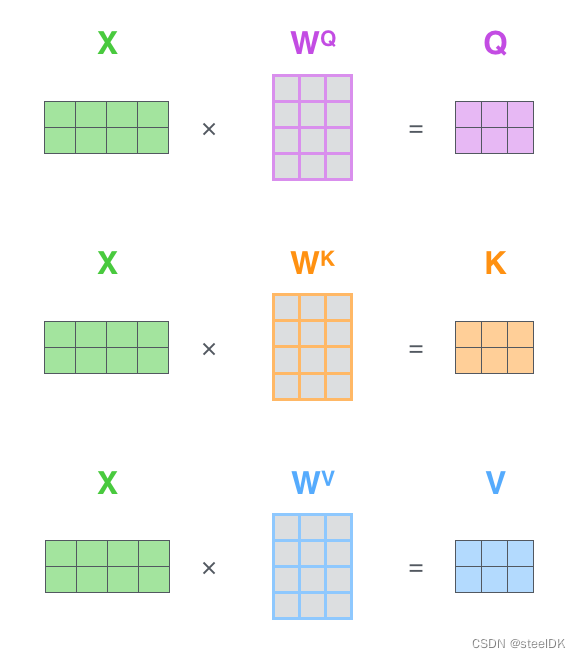
第二步:Q乘以 K T K^{T} KT,得到相似度。
比较经典的就是下图的示例,图片来源:The llustrated Transformer
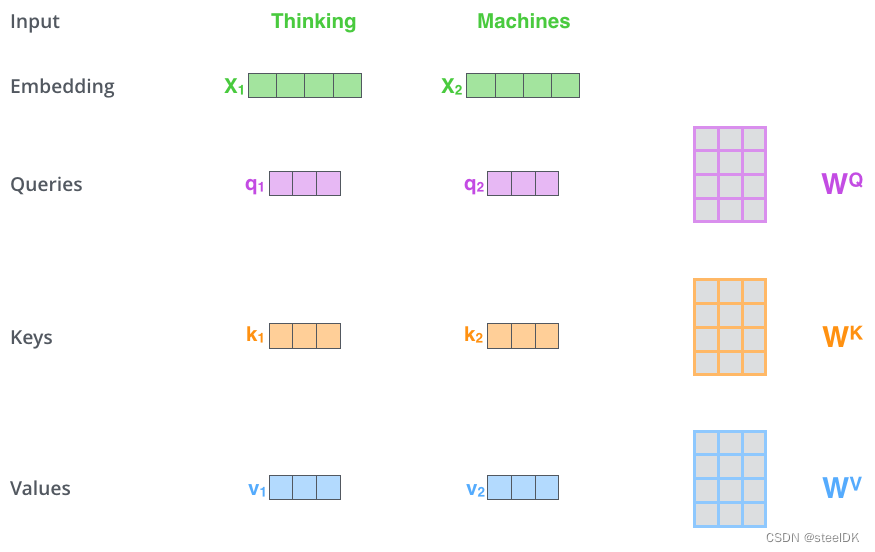
解读:假设有两个单词Thinking和Machines,这两个单词经过Embedding之后得到了代表这两个词的词向量X1和X2,如图四绿色所示。将这两个词向量X1和X2分别乘以矩阵 W Q W^{Q} WQ得到q1、q2查询向量,分别乘以 W K W^{K} WK得到k1、k2向量,分别乘以 W V W^{V} WV得到v1、v2向量,至此,代表这两个单词的q,k,v向量均已得到,接着就是计算两个词向量之间的相似度,如下图所示:
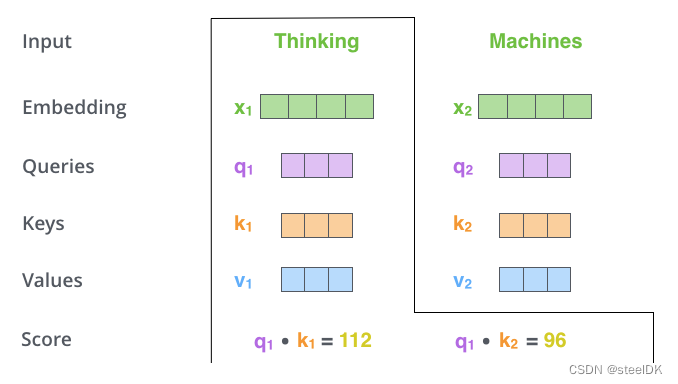
上图五演示的是代表单词Thinking的查询向量q1与自己的k1和单词Machines的k2分别相乘,得到Score,这里假设q1乘以k1的计算结果为112,q1乘以k2的计算结果为96,这两个结果就代表了单词Thinking与Thinking、单词Thinking与Machines之间的相似度。
第三步:将得到的相似度除以 d k \sqrt{d_k} dk,然后进行softmax归一化,得到每个值都是大于0小于1的权重矩阵,且每行总和为1。
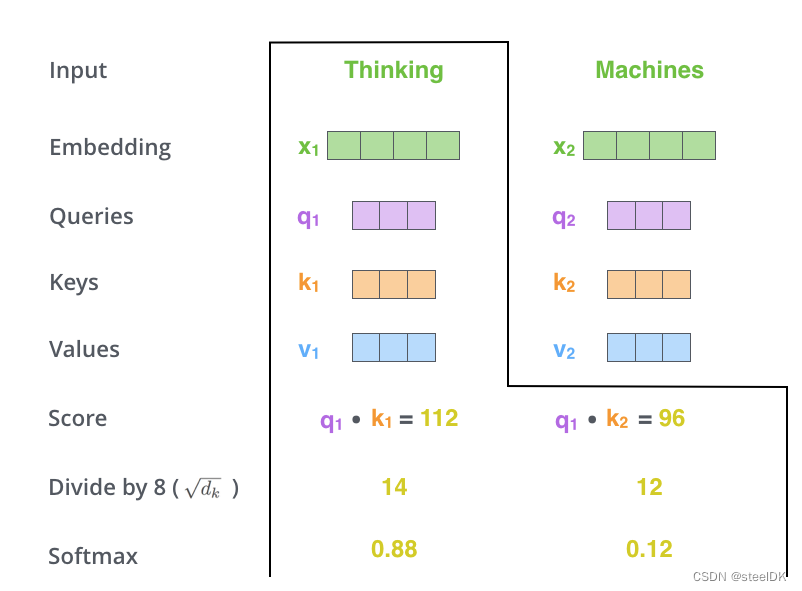
解读:在第三步中我们得到了相似度,即图中的Score,对两个单词的Score除以 d k \sqrt{d_k} dk,然后进行softmax归一化, d k d_k dk是词向量x的维度,这里原文作者假设为64维了,所以开根号是8(不要计较文中所画X和q、k、v的维度数,仅仅是演示,知道计算流程即可)。通过softmax归一化之后,得到0.88和0.12,显然,和为1。
第四步:将第三步得到的权重矩阵与V相乘,进行加权求和。
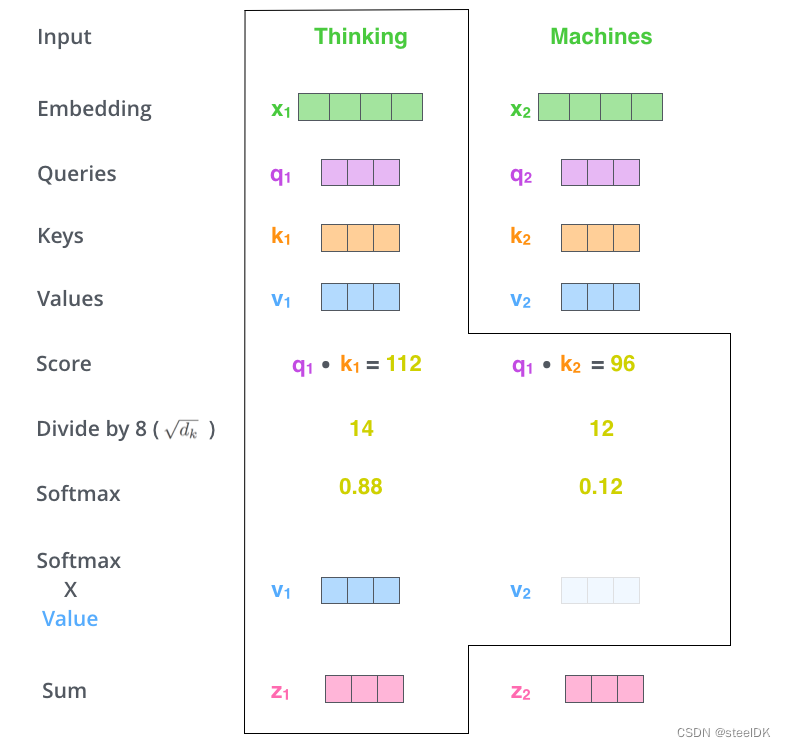
解读:将softmax得到的结果与与最开始得到v1和v2向量相乘,然后求和得到z1。注意,这几幅图都是以词Thingking为示例的,一个词向量得到一个z1。随后按照上述流程再计算词Machines与本身和Thingking之间相似度,最终经过softmax和Sum,同样得到z2。那么z1就代表了单词Thingking与这个句子中所有单词之间的关联,那么z2就代表了单词Thingking与这个句子中所有单词之间的关联。
仔细阅读会发现,我们上述所有的计算都是围绕着公式1进行的,下面给一个形象化的公式:

在获取了Q、K、V矩阵之后,主要进行的就是矩阵乘法。
3、单头注意力机制与多头注意力机制
在第二节当中,我们学习的都是单头注意力机制,在实际应用中,我们用的都是多头注意力机制,单头的意思是一个句子只有一组Q、K、V矩阵,多头的意思是在最开始生成Q、K、V矩阵的时候,同时生成多组Q、K、V矩阵,同时进行操作。我们以两组为例,示意图如下:
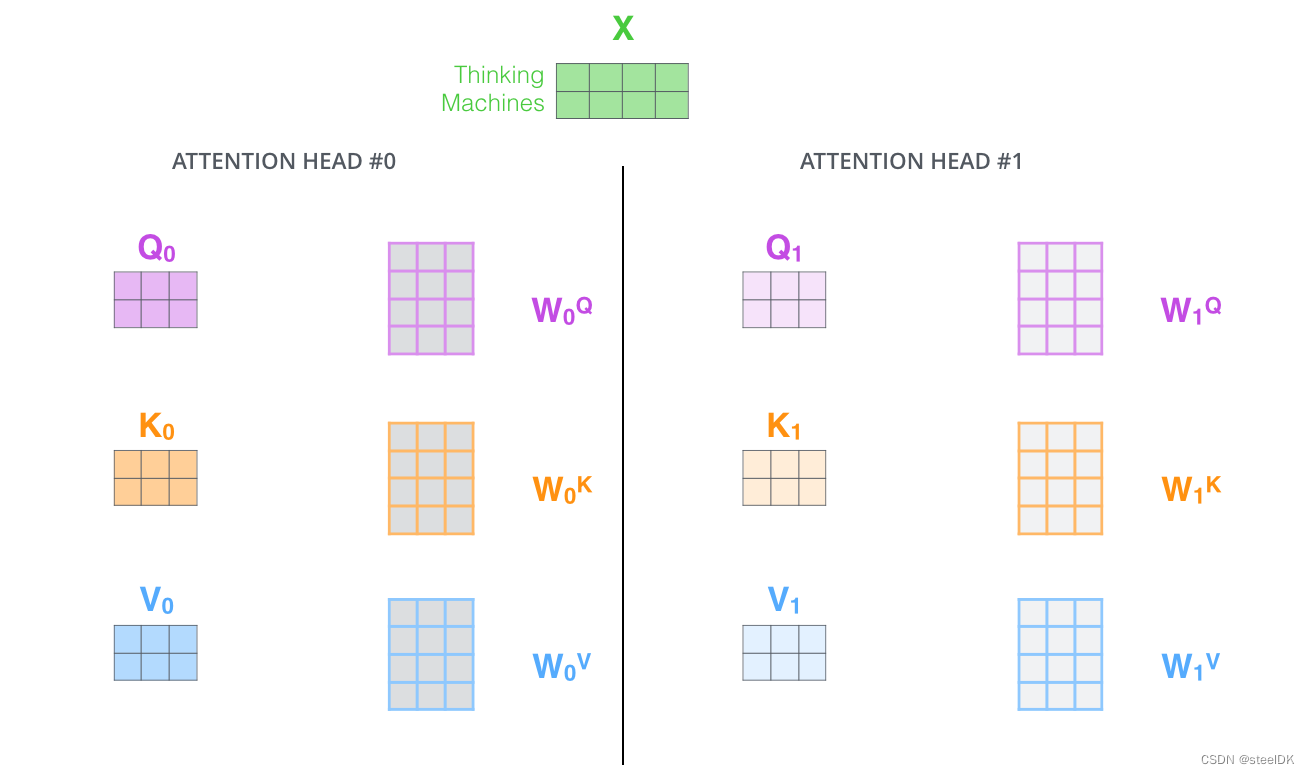
下面是一个8头的例子,计算流程如下:
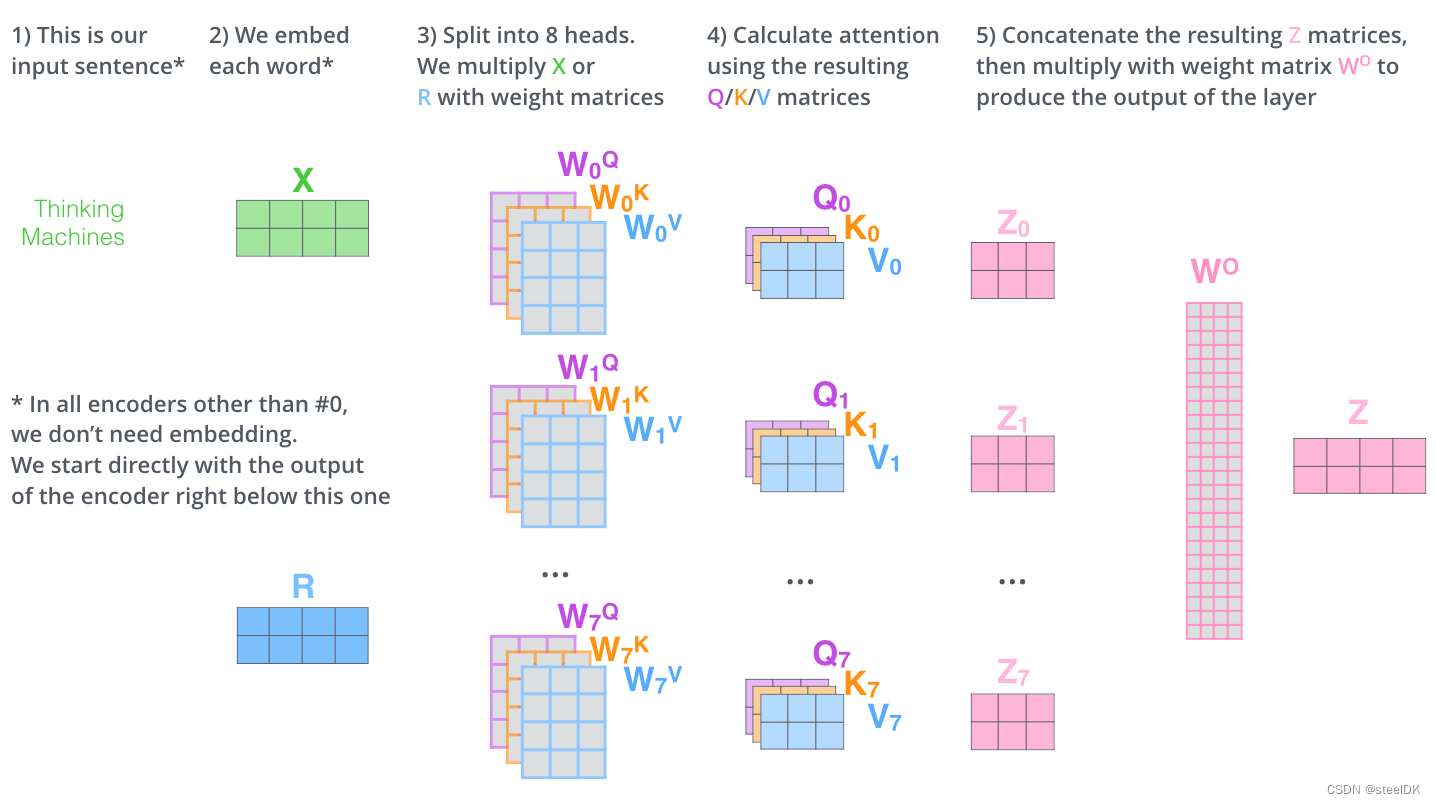
上图中的 W O W^{O} WO是output输出的权重的矩阵,目的是将前面8个头提取的信息进行汇总,是个在反向传播中需要更新的参数矩阵。
4、代码
4.1 代码1
此代码参考注意力,多头注意力,自注意力及Pytorch实现。
代码特点:直观、易于理解。
多头注意力代码是在单头注意力的基础上写成的,单头注意力的pytorch代码如下:
class ScaledDotProductAttention(nn.Module):""" Scaled Dot-Product Attention """def __init__(self, scale):super().__init__()self.scale = scaleself.softmax = nn.Softmax(dim=2)def forward(self, q, k, v, mask=None):u = torch.bmm(q, k.transpose(1, 2)) # 1.Matmulu = u / self.scale # 2.Scaleif mask is not None:u = u.masked_fill(mask, -np.inf) # 3.Maskattn = self.softmax(u) # 4.Softmaxoutput = torch.bmm(attn, v) # 5.Outputreturn attn, outputif __name__ == "__main__":n_q, n_k, n_v = 2, 4, 4d_q, d_k, d_v = 128, 128, 64q = torch.randn(batch, n_q, d_q)k = torch.randn(batch, n_k, d_k)v = torch.randn(batch, n_v, d_v)mask = torch.zeros(batch, n_q, n_k).bool()attention = ScaledDotProductAttention(scale=np.power(d_k, 0.5))attn, output = attention(q, k, v, mask=mask)print(attn)print(output)
多头注意力机制的pytorch代码如下:
class MultiHeadAttention(nn.Module):""" Multi-Head Attention """def __init__(self, n_head, d_k_, d_v_, d_k, d_v, d_o):super().__init__()self.n_head = n_headself.d_k = d_kself.d_v = d_vself.fc_q = nn.Linear(d_k_, n_head * d_k)self.fc_k = nn.Linear(d_k_, n_head * d_k)self.fc_v = nn.Linear(d_v_, n_head * d_v)self.attention = ScaledDotProductAttention(scale=np.power(d_k, 0.5))self.fc_o = nn.Linear(n_head * d_v, d_o)def forward(self, q, k, v, mask=None):n_head, d_q, d_k, d_v = self.n_head, self.d_k, self.d_k, self.d_vbatch, n_q, d_q_ = q.size()batch, n_k, d_k_ = k.size()batch, n_v, d_v_ = v.size()q = self.fc_q(q) # 1.单头变多头k = self.fc_k(k)v = self.fc_v(v)q = q.view(batch, n_q, n_head, d_q).permute(2, 0, 1, 3).contiguous().view(-1, n_q, d_q)k = k.view(batch, n_k, n_head, d_k).permute(2, 0, 1, 3).contiguous().view(-1, n_k, d_k)v = v.view(batch, n_v, n_head, d_v).permute(2, 0, 1, 3).contiguous().view(-1, n_v, d_v)if mask is not None:mask = mask.repeat(n_head, 1, 1)attn, output = self.attention(q, k, v, mask=mask) # 2.当成单头注意力求输出output = output.view(n_head, batch, n_q, d_v).permute(1, 2, 0, 3).contiguous().view(batch, n_q, -1) # 3.Concatoutput = self.fc_o(output) # 4.仿射变换得到最终输出return attn, outputif __name__ == "__main__":n_q, n_k, n_v = 2, 4, 4d_q_, d_k_, d_v_ = 128, 128, 64q = torch.randn(batch, n_q, d_q_)k = torch.randn(batch, n_k, d_k_)v = torch.randn(batch, n_v, d_v_) mask = torch.zeros(batch, n_q, n_k).bool()mha = MultiHeadAttention(n_head=8, d_k_=128, d_v_=64, d_k=256, d_v=128, d_o=128)attn, output = mha(q, k, v, mask=mask)print(attn.size())print(output.size())
4.2 代码2
此代码参考attention-is-all-you-need-pytorch/transformer/SubLayers.py。
代码特点:实际应用中的代码,与代码1有些许差别
多头注意力代码是在单头注意力的基础上写成的,单头注意力的pytorch代码如下:
import torch
import torch.nn as nn
import torch.nn.functional as F
class ScaledDotProductAttention(nn.Module):''' Scaled Dot-Product Attention '''def __init__(self, temperature, attn_dropout=0.1):super().__init__()self.temperature = temperatureself.dropout = nn.Dropout(attn_dropout)def forward(self, q, k, v, mask=None):attn = torch.matmul(q / self.temperature, k.transpose(2, 3))if mask is not None:attn = attn.masked_fill(mask == 0, -1e9)attn = self.dropout(F.softmax(attn, dim=-1))output = torch.matmul(attn, v)return output, attn
多头注意力机制的pytorch代码如下:
import numpy as np
import torch.nn as nn
import torch.nn.functional as
class MultiHeadAttention(nn.Module):''' Multi-Head Attention module '''def __init__(self, n_head, d_model, d_k, d_v, dropout=0.1):super().__init__()self.n_head = n_headself.d_k = d_kself.d_v = d_vself.w_qs = nn.Linear(d_model, n_head * d_k, bias=False)self.w_ks = nn.Linear(d_model, n_head * d_k, bias=False)self.w_vs = nn.Linear(d_model, n_head * d_v, bias=False)self.fc = nn.Linear(n_head * d_v, d_model, bias=False)self.attention = ScaledDotProductAttention(temperature=d_k ** 0.5)self.dropout = nn.Dropout(dropout)self.layer_norm = nn.LayerNorm(d_model, eps=1e-6)def forward(self, q, k, v, mask=None):d_k, d_v, n_head = self.d_k, self.d_v, self.n_headsz_b, len_q, len_k, len_v = q.size(0), q.size(1), k.size(1), v.size(1)residual = q# Pass through the pre-attention projection: b x lq x (n*dv)# Separate different heads: b x lq x n x dvq = self.w_qs(q).view(sz_b, len_q, n_head, d_k)k = self.w_ks(k).view(sz_b, len_k, n_head, d_k)v = self.w_vs(v).view(sz_b, len_v, n_head, d_v)# Transpose for attention dot product: b x n x lq x dvq, k, v = q.transpose(1, 2), k.transpose(1, 2), v.transpose(1, 2)if mask is not None:mask = mask.unsqueeze(1) # For head axis broadcasting.q, attn = self.attention(q, k, v, mask=mask)# Transpose to move the head dimension back: b x lq x n x dv# Combine the last two dimensions to concatenate all the heads # together: b x lq x (n*dv)q = q.transpose(1, 2).contiguous().view(sz_b, len_q, -1)q = self.dropout(self.fc(q))q += residualq = self.layer_norm(q)return q, attn
后续会增加代码相关的解释。
待更~ 2023/04/07
相关文章:

Transformer中的注意力机制及代码
文章目录 1、简介2、原理2.1 什么是注意力机制2.2 注意力机制在NLP中解决了什么问题2.3 注意力机制公式解读2.4 注意力机制计算过程 3、单头注意力机制与多头注意力机制4、代码4.1 代码14.2 代码2 1、简介 最近在学习transformer,首先学习了多头注意力机制…...

ChatGPT在连续追问下对多线程和双重检查锁模式的理解--已经超越中级程序员
一、问: private static final Map<Method, GZHttpClientResultModel> CACHE_RESULT_MODEL new ConcurrentHashMap<>();public void abc(Method method){cacheResultMode(method);GZHttpClientResultModel model CACHE_RESULT_MODEL.get(method);}pr…...

每天一道大厂SQL题【Day22】华泰证券真题实战(四)
每天一道大厂SQL题【Day22】华泰证券真题实战(四) 大家好,我是Maynor。相信大家和我一样,都有一个大厂梦,作为一名资深大数据选手,深知SQL重要性,接下来我准备用100天时间,基于大数据岗面试中的经典SQL题&…...
【智能电网】智能电网中针对DOS和FDIA的弹性分布式EMA(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...

IDEA 创建微服务项目实例
🎈 作者:Linux猿 🎈 简介:CSDN博客专家🏆,华为云享专家🏆,Linux、C/C++、云计算、物联网、面试、刷题、算法尽管咨询我,关注我,有问题私聊! 🎈 关注专栏:C/C++面试通关【精讲】 优质好文持续更新中……🚀🚀🚀 🎈 欢迎小伙伴们点赞👍、收藏⭐、留…...

注册苹果开发者账号的方法
在2020年以前,注册苹果开发者账号后,就可以生成证书。 但2020年后,因为注册苹果开发者账号需要使用Apple Developer app注册开发者账号,所以需要缴费才能创建ios证书了。 所以新政策出来后,注册苹果开发者账号&#…...

OpenCV2 计算机视觉应用编程秘籍:1~5
原文:OpenCV2 Computer Vision Application Programming Cookbook 协议:CC BY-NC-SA 4.0 译者:飞龙 本文来自【ApacheCN 计算机视觉 译文集】,采用译后编辑(MTPE)流程来尽可能提升效率。 当别人说你没有底线…...
Domino自带的JSON校验工具
大家好,才是真的好。 JSON数据在Notes/Domino已经变得非常重要。从Domino 10开始,在LotusScript语言中就加入了对JSON数据处理功能。在管理中,我们知道,从Domino 12版本开始就支持Domino自动化配置,也是使用JSON数据作…...
CentOS(linux)使用Docker安装nacos
1. 拉取nacos镜像 docker pull nacos/nacos-server:2.0.3 2. 创建所需文件夹(以安装在home目录下为例) 1) 创建conf文件夹 mkdir -p /home/nacos/conf a. 新增文件application.properties(或者不增加该文件,会使用默认的) 文件内容如下: # spring server.servlet.contextP…...

无线测温在线监测系统工作原理与产品选型
摘要:本文首先介绍了无线测温在线监测系统的基本工作原理以及软硬件组成,重点介绍了在线监测的无线测温技术特点。在此研究基础上,探讨了无线测温在线监测系统在实际工作场景中的应用案例,证明了其在温度检测方面的重要应用价值。…...
Nginx rewrite ——重写跳转
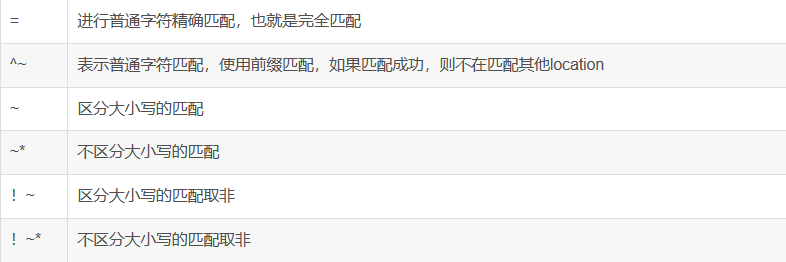
Nginx常见模块 http http块是Nginx服务器配置中的重要部分,代理、缓存和日志定义等绝大多数的功能和第三方模块的配置都可以放在这模块中。作用包括:文件引入、MIME-Type定义、日志自定义、是否使用sendfile传输文件、连接超时时间、单连接请求数上限等…...

【华为OD机试真题 C++】1038 - 全量和已占用字符集 | 机试题+算法思路+考点+代码解析
文章目录 一、题目🔸题目描述🔸输入输出🔸样例1二、代码参考作者:KJ.JK🌈 🌈 🌈 🌈 🌈 🌈 🌈 🌈 🌈 🌈 🌈 🌈 🌈 🍂个人博客首页: KJ.JK 💖系列专栏:华为OD机试真题(C++) 一、题目 🔸题目描述 所谓水仙花数,是指一个n位的正整数…...

网络中的网关和物联网的网关区别 局域网 路由器 交换机 服务器
网关:是个概念。连接两种不同的网络。例如局域网要与外部通信,需要经过网关。 设备和设备之间的通信,转换协议需要网关 路由器里有功能是对网关这个概念的实现。 所以网关它可以是路由器,交换机或者是PC。 路由器有网关功能&a…...

2023 年嵌入式世界的3 大趋势分析
目录 大家好,本文讲解了嵌入式发展的3个大趋势,分享给大家。 趋势#1 – Visual Studio Code Integration 趋势#2 –支持“现代”软件流程 趋势 #3 – 在设计中利用 AI 和 ML 结论 大家好,本文讲解了嵌入式发展的3个大趋势,分享…...

基于 DolphinDB 机器学习的出租车行程时间预测
DolphinDB 集高性能时序数据库与全面的分析功能为一体,可用于海量结构化数据的存储、查询、分析、实时计算等,在工业物联网场景中应用广泛。本文以纽约出租车行程时间预测为例,介绍如何使用 DolphinDB 训练机器学习模型,并进行实时…...

Python调用最小二乘法
文章目录 numpy实现scipy封装速度对比 所谓线性最小二乘法,可以理解为是解方程的延续,区别在于,当未知量远小于方程数的时候,将得到一个无解的问题。最小二乘法的实质,是保证误差最小的情况下对未知数进行赋值。 最小…...

15.数据表格.上
本节课我们来开始了解 Layui 的内置模块:table 数据表格。 一.基本使用 1. table 模块,通过异步加载数据来渲染表格来展现数据内容; <table id"table"></table> layui.use([table], () > { const table …...

在poetry虚拟环境下打包exe
本博客介绍了在poetry虚拟环境下打包exe的流程,包含两个部分 打包的基本流程打包过程中遇到的问题 打包的基本流程 copy打包工具到本地,(share:\公用共享\芯片部\乔羽\img_generate\系统部提供的打包exe工具) 用poetry搭建虚拟环境 在打包…...
【Unity VR开发】结合VRTK4.0:高亮与标签
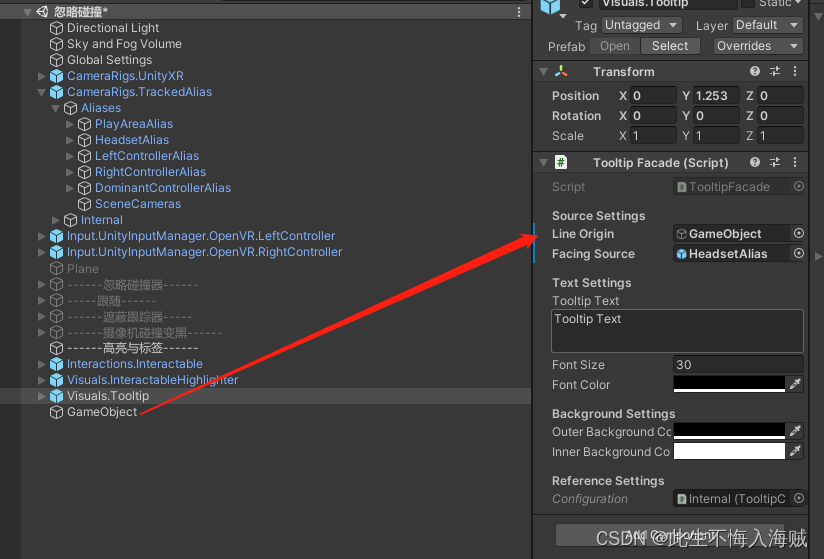
语录: 信仰到底是什么呢,就是纵身一跃,就是我们跟神之间一个永远的约定,是舍弃日的去开始新的生活;信仰就是从今以后,再也不要放开你的手。 前言: Interactable Highlighter :当我们的手柄触碰…...

有了MySQL,为什么还要有NoSQL
🏆今日学习目标: 🍀MySQL和NoSQL的区别 ✅创作者:林在闪闪发光 ⏰预计时间:30分钟 🎉个人主页:林在闪闪发光的个人主页 🍁林在闪闪发光的个人社区,欢迎你的加入: 林在闪闪…...

【大模型RAG】拍照搜题技术架构速览:三层管道、两级检索、兜底大模型
摘要 拍照搜题系统采用“三层管道(多模态 OCR → 语义检索 → 答案渲染)、两级检索(倒排 BM25 向量 HNSW)并以大语言模型兜底”的整体框架: 多模态 OCR 层 将题目图片经过超分、去噪、倾斜校正后,分别用…...
)
Java 语言特性(面试系列1)
一、面向对象编程 1. 封装(Encapsulation) 定义:将数据(属性)和操作数据的方法绑定在一起,通过访问控制符(private、protected、public)隐藏内部实现细节。示例: public …...

Qt/C++开发监控GB28181系统/取流协议/同时支持udp/tcp被动/tcp主动
一、前言说明 在2011版本的gb28181协议中,拉取视频流只要求udp方式,从2016开始要求新增支持tcp被动和tcp主动两种方式,udp理论上会丢包的,所以实际使用过程可能会出现画面花屏的情况,而tcp肯定不丢包,起码…...

MySQL 隔离级别:脏读、幻读及不可重复读的原理与示例
一、MySQL 隔离级别 MySQL 提供了四种隔离级别,用于控制事务之间的并发访问以及数据的可见性,不同隔离级别对脏读、幻读、不可重复读这几种并发数据问题有着不同的处理方式,具体如下: 隔离级别脏读不可重复读幻读性能特点及锁机制读未提交(READ UNCOMMITTED)允许出现允许…...

CentOS下的分布式内存计算Spark环境部署
一、Spark 核心架构与应用场景 1.1 分布式计算引擎的核心优势 Spark 是基于内存的分布式计算框架,相比 MapReduce 具有以下核心优势: 内存计算:数据可常驻内存,迭代计算性能提升 10-100 倍(文档段落:3-79…...

转转集团旗下首家二手多品类循环仓店“超级转转”开业
6月9日,国内领先的循环经济企业转转集团旗下首家二手多品类循环仓店“超级转转”正式开业。 转转集团创始人兼CEO黄炜、转转循环时尚发起人朱珠、转转集团COO兼红布林CEO胡伟琨、王府井集团副总裁祝捷等出席了开业剪彩仪式。 据「TMT星球」了解,“超级…...

Spring数据访问模块设计
前面我们已经完成了IoC和web模块的设计,聪明的码友立马就知道了,该到数据访问模块了,要不就这俩玩个6啊,查库势在必行,至此,它来了。 一、核心设计理念 1、痛点在哪 应用离不开数据(数据库、No…...

使用 SymPy 进行向量和矩阵的高级操作
在科学计算和工程领域,向量和矩阵操作是解决问题的核心技能之一。Python 的 SymPy 库提供了强大的符号计算功能,能够高效地处理向量和矩阵的各种操作。本文将深入探讨如何使用 SymPy 进行向量和矩阵的创建、合并以及维度拓展等操作,并通过具体…...

基于 TAPD 进行项目管理
起因 自己写了个小工具,仓库用的Github。之前在用markdown进行需求管理,现在随着功能的增加,感觉有点难以管理了,所以用TAPD这个工具进行需求、Bug管理。 操作流程 注册 TAPD,需要提供一个企业名新建一个项目&#…...

PAN/FPN
import torch import torch.nn as nn import torch.nn.functional as F import mathclass LowResQueryHighResKVAttention(nn.Module):"""方案 1: 低分辨率特征 (Query) 查询高分辨率特征 (Key, Value).输出分辨率与低分辨率输入相同。"""def __…...
