CF1707E Replace
题目描述
给定一个长为 nnn 的序列 a1,…,ana_1,\ldots,a_na1,…,an,其中对于任意的 iii 满足 1≤ai≤n1 \leq a_i \leq n1≤ai≤n。
定义一个二元组函数如下:
f((l,r))=(min{al,…,ar},max{al,…,ar})(l≤r)f((l,r))=(\min\{a_l,\ldots,a_r\},\max\{a_l,\ldots,a_r\})(l \leq r)f((l,r))=(min{al,…,ar},max{al,…,ar})(l≤r)
你需要回答 qqq 次询问,每次给定 (li,ri)(l_i,r_i)(li,ri),问其最少经过多少次 fff 的调用(即 (l,r)→f((l,r))(l,r) \rightarrow f((l,r))(l,r)→f((l,r)))使得 (li,ri)(l_i,r_i)(li,ri) 变成 (1,n)(1,n)(1,n),若无解请输出 -1。
题解
智慧的性质题
首先注意到f((l,r))=⋃i=lr−1f((i,i+1))f((l,r))=\bigcup_{i=l}^{r-1}f((i,i+1))f((l,r))=⋃i=lr−1f((i,i+1))
发现可以推广到fk((l,r))=⋃i=lr−1fk((i,i+1))f^k((l,r))=\bigcup_{i=l}^{r-1}f^k((i,i+1))fk((l,r))=⋃i=lr−1fk((i,i+1)),可以用归纳法证明
接下来的做法就容易可以想出了
设Fi,j=f2i((j,j+1))F_{i,j}=f^{2^i}((j,j+1))Fi,j=f2i((j,j+1)),然后倍增解决,合并区间可以用线段树,长度为111的线段需要特别处理
code\text{code}code
#include<cstdio>
#include<algorithm>
#define ll long long
using namespace std;
void read(int &res)
{res=0;char ch=getchar();while(ch<'0'||ch>'9') ch=getchar();while('0'<=ch&&ch<='9') res=(res<<1)+(res<<3)+(ch^48),ch=getchar();
}
const int N=1e5+100,B=40;
int n,q,a[N+10];
struct seg
{int l,r;
}f[B+10][N+10];
int g[B+10][N+10];
seg merge(seg a,seg b){return (seg){min(a.l,b.l),max(a.r,b.r)};}
struct SEG
{seg t[N<<2|1];#define ls (p<<1)#define rs (p<<1|1)#define mid ((l+r)>>1)void build(seg *f,int p=1,int l=1,int r=n-1){if(l==r){t[p]=f[l];return;}build(f,ls,l,mid),build(f,rs,mid+1,r);t[p]=merge(t[ls],t[rs]);}seg query(int L,int R,int p=1,int l=1,int r=n-1){if(L<=l&&r<=R) return t[p];if(R<=mid) return query(L,R,ls,l,mid);else if(L>mid) return query(L,R,rs,mid+1,r);else return merge(query(L,R,ls,l,mid),query(L,R,rs,mid+1,r));}#undef ls#undef rs#undef mid
}t[B+10];
int main()
{
// freopen("a.in","r",stdin);read(n),read(q);if(n==1){for(;q--;) printf("0\n");return 0;}for(int i=1;i<=n;i++) read(a[i]);for(int i=1;i<n;i++) f[0][i]=(seg){min(a[i],a[i+1]),max(a[i],a[i+1])},g[0][i]=a[i];t[0].build(f[0]);for(int j=1;j<=B;j++){for(int i=1;i<n;i++){if(f[j-1][i].l==f[j-1][i].r) f[j][i]=(seg){g[j-1][f[j-1][i].l],g[j-1][f[j-1][i].l]};else f[j][i]=t[j-1].query(f[j-1][i].l,f[j-1][i].r-1);}t[j].build(f[j]);for(int i=1;i<=n;i++) g[j][i]=g[j-1][g[j-1][i]];}for(int l,r;q--;){read(l),read(r);if(l==1&&r==n){printf("0\n");continue;}ll ans=0;if(l!=r)for(int i=B;i>=0;i--){seg tmp=t[i].query(l,r-1);if(tmp.l!=1||tmp.r!=n){l=tmp.l,r=tmp.r;ans+=(1ll<<i);}if(l==r) break;}if(l==r) printf("-1\n");else{seg tmp=t[0].query(l,r-1);if(tmp.l==1&&tmp.r==n) printf("%lld\n",ans+1);else printf("-1\n");}}return 0;
}
相关文章:

CF1707E Replace
题目描述 给定一个长为 nnn 的序列 a1,…,ana_1,\ldots,a_na1,…,an,其中对于任意的 iii 满足 1≤ai≤n1 \leq a_i \leq n1≤ai≤n。 定义一个二元组函数如下: f((l,r))(min{al,…,ar},max{al,…,ar})(l≤r)f((l,r))(\min\{a_l,\ldots,a_r\}…...
【Hello Linux】Linux工具介绍 (make/makefile git)
作者:小萌新 专栏:Linux 作者简介:大二学生 希望能和大家一起进步! 本篇博客简介:介绍Linux的常用工具make/makefile git Linux项目自动化构建工具 – make/Makefile 背景 会不会写Makefile 从侧面说明了一个人是否具…...
享元模式flyweight
享元模式属于结构型模式。享元模式是池技术的重要实现方式,它可以减少重复对象的创建,使用缓存来共享对象,从而降低内存的使用。细粒度的对象其状态可以分为两种:内部状态和外部状态。应用场景系统存在大量相似或相同的对象。外部…...
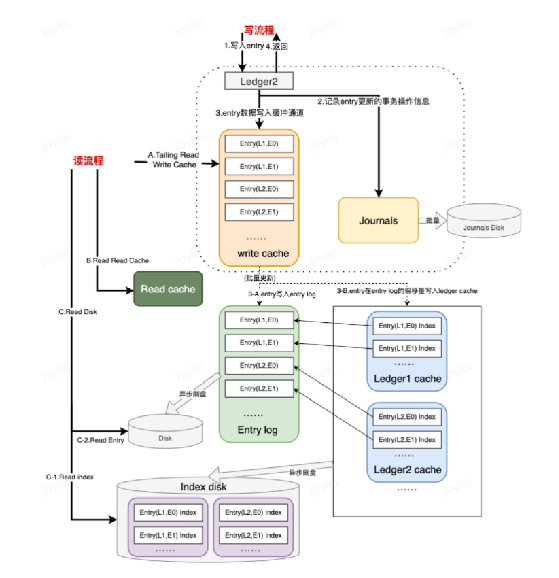
Pulsar
一、简介Apache Pulsar是Apache软件基金会顶级项目,是下一代云原生分布式消息流平台,集消息、存储、轻量化函数式计算为一体,采用计算与存储分离架构设计,支持多租户、持久化存储、多机房跨区域数据复制,具有强一致性、…...

项目介绍 + 定长内存池设计及实现
你好,我是安然无虞。 文章目录项目介绍当前项目做的是什么?技术栈内存池是什么?池化技术内存池内存池主要解决的问题malloc定长内存池学习目的定长内存池设计项目介绍 当前项目做的是什么? 这个项目是实现一个高并发的内存池, 它的原型是 Google 的一个开源项…...

Linux--线程安全的单例模式--自旋锁--0211
1. 线程安全的单例模式 1.1 什么是单例模式 某些类, 只应该具有一个对象(实例), 就称之为单例. 1.1.1 懒汉方式实现单例模式 以上篇博文的线程池为例 Liunx--线程池的实现--0208 09_Gosolo!的博客-CSDN博客 实现懒汉模式首先要先将构造函数私有化,…...
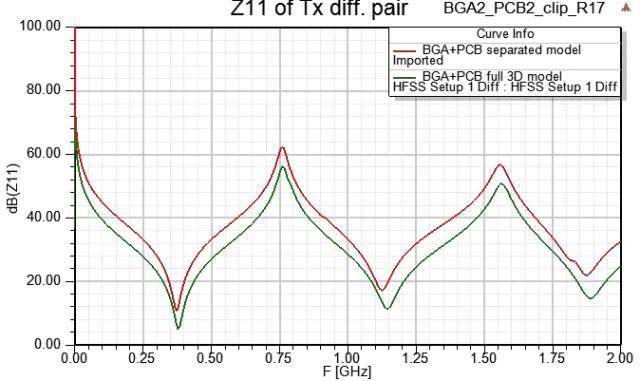
图文解说S参数(进阶篇)
S参数是RF工程师/SI工程师必须掌握的内容,业界已有多位大师写过关于S参数的文章,即便如此,在相关领域打滚多年的人, 可能还是会被一些问题困扰着。你懂S参数吗? 图文解说S参数(基础篇) 请继续往下看...台湾…...
Sentinel源码阅读
基础介绍 Sentinel 的使用可以分为两个部分: 核心库(Java 客户端):不依赖任何框架/库,能够运行于 Java 8 及以上的版本的运行时环境,同时对 Dubbo / Spring Cloud 等框架也有较好的支持(见 主流框架适配&…...
2023年浙江食品安全管理员考试真题题库及答案
百分百题库提供食品安全管理员考试试题、食品安全管理员考试预测题、食品安全管理员考试真题、食品安全管理员证考试题库等,提供在线做题刷题,在线模拟考试,助你考试轻松过关。 一、判断题 7.(重点)《餐饮服务食品安全…...
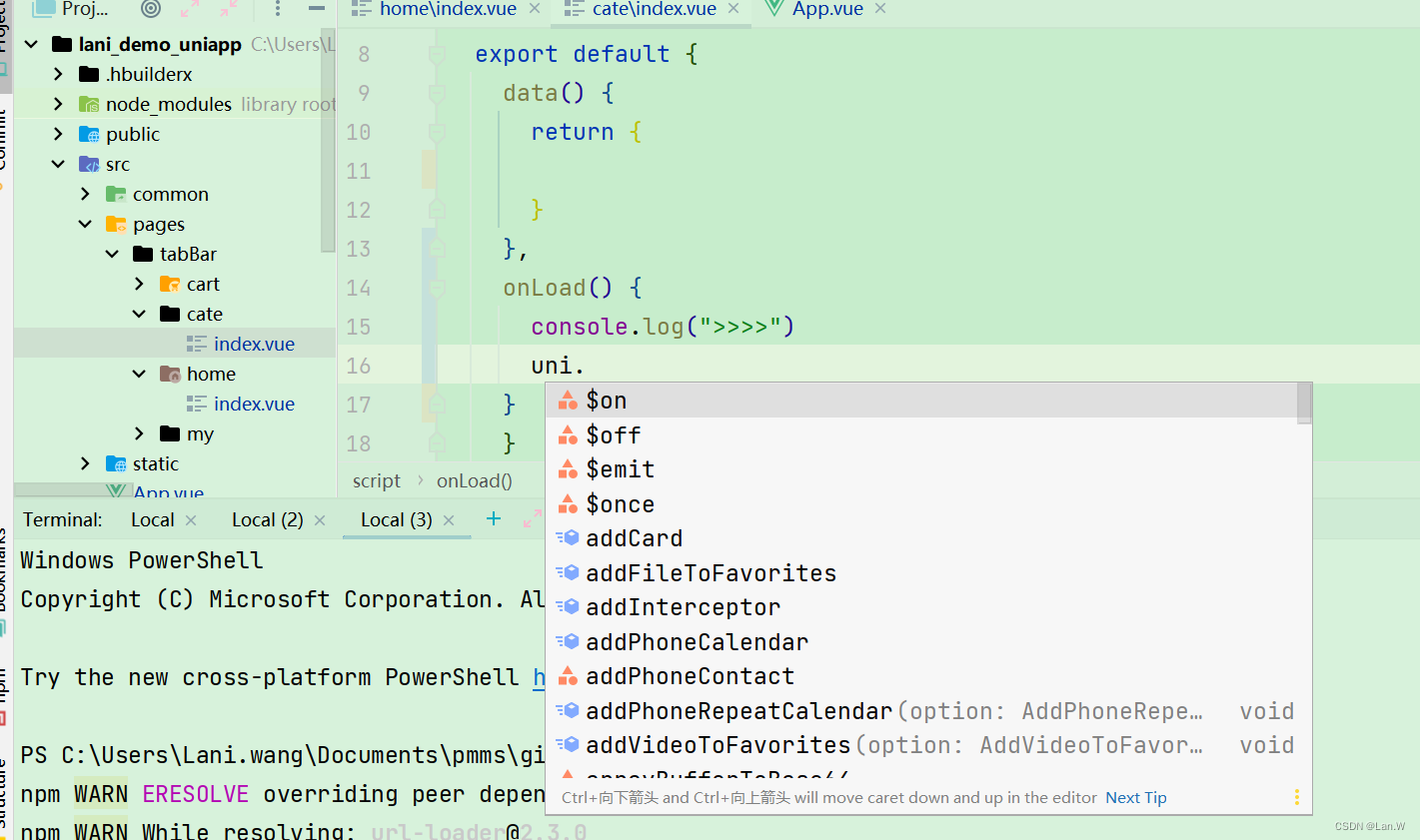
Webstorm 代码没有提示,uniapp 标签报错
问题 项目是用脚手架创建的: vue create -p dcloudio/uni-preset-vue my-project 打开之后,添加view标签警告报错的。代码也没有提示,按官方说法:CLI 工程默认带了 uni-app 语法提示和 5App 语法提示。 但是我这里就是有问题。…...

MySQL-Innodb引擎事务原理
文章目录1.事务介绍2 事务特性3. 事务的实现原理4 redo log 保证持久性5 undo log 保证原子性6 MVCC 概念6.1 隐藏字段6.2 版本链6.3 ReadView6.3.1readview 版本控制规则7 隔离性 实现7.2 隔离性- REPEATABLE READ 可重复读下8 一致性1.事务介绍 事务是一组操作的集合…...

Linux操作系统学习(了解环境变量)
文章目录环境变量初识除了上述介绍的PATH,还有一些常见的环境变量如:查看环境变量方法 :环境变量的基本概念:本地变量:环境变量初识 环境变量解释起来比较抽象,先看示例: #include <stdio.…...
数据分析思维(六)|循环/闭环思维
循环/闭环思维 1、概念 在很多的分析场景下,我们需要按照一套流程反复分析,而不是进行一次性的分析,也就是说这套流程的结果会成为该流程的新一次输入,从而形成一个闭环,此时的分析思维我们称之为循环/闭环思维。 常…...

C++:类和对象(下)
文章目录1 再谈构造函数1.1 构造函数体赋值1.2 初始化列表1.3 explicit关键字2 static成员2.1 概念2.2 特性3 友元3.1 友元函数(流插入(<<)及流提取(>>)运算符重载)3.2 友元类4 内部类5 匿名对…...

ASP.NET Core MVC 项目 AOP之IResultFilter和IAsyncResultFilter
目录 一:说明 二:IActionFilter同步 三:IAsyncActionFilter异步 一:说明 IResultFilter同步过滤器与IAsyncResultFilter异步过滤器常常被用作于渲染视图或处理结果。 IResultFilter同步过滤器执行顺序: 1:执行控制器中的构造函数,实例化控制器 2:执行具体的Acti…...
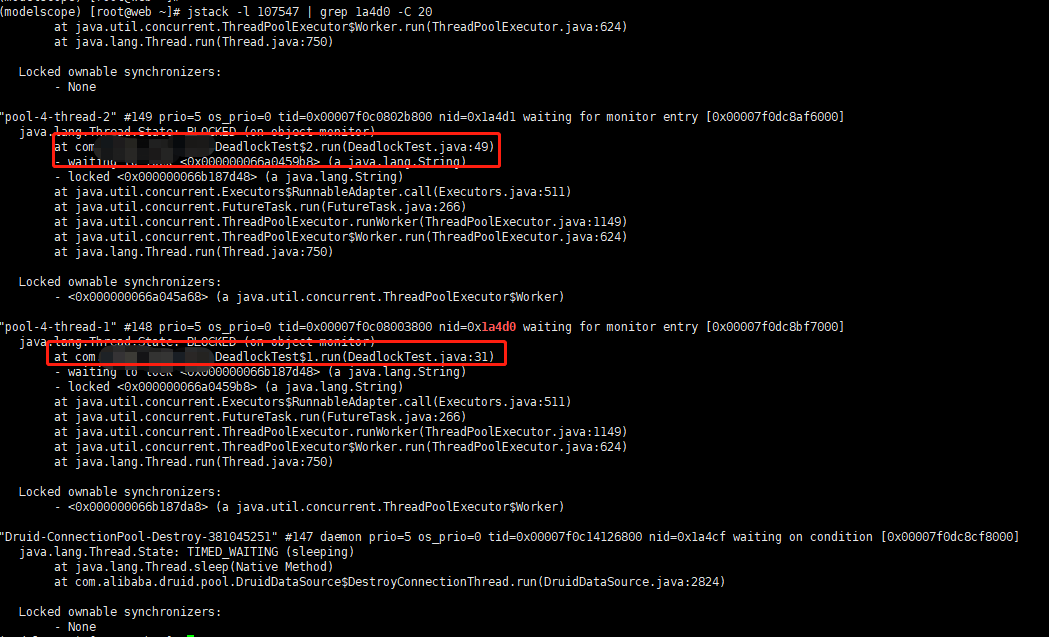
jstack排查cpu占用高[复习]
这样就可以看到占用CPU高的代码位置。 总结:就是先查到占用高的应用和具体的线程,然后根据线程到堆积信息查找即可。 不过堆栈信息非十进制,需提前把线程号转为十六进制。 这样就可以看到占用CPU高的代码位置。 总结:就是先查到…...
网络安全-Pyhton环境搭建
网络安全-Pyhton环境搭建 https://www.kali.org/get-kali/#kali-installer-images—kali官网下载地址 python这个东东呢 是目前来说最简单,方便的开源的脚本语言 广泛用于Web开发,AI,网站开发等领域 python要装2和3 为什么要安装两个版本…...

SpringBoot Mybatis 分页实战
pageInfo的属性 pageNum:当前页 pageSize:页面数据量 startRow:当前页首条数据为总数据的第几条 endRow:当前页最后一条数据为总数据的第几条 total:总数据量 pages:总页面数 listPage{}结果集 reasonable …...

计算机断层扫描结肠镜和全自动骨密度仪在一次检查中的可行性
计算机断层扫描结肠镜和全自动骨密度仪在一次检查中的可行性 Feasibility of Simultaneous Computed Tomographic Colonography and Fully Automated Bone Mineral Densitometry in a Single Examination 简单总结: 数据:患者的结肠镜检查和腹部CT检查…...
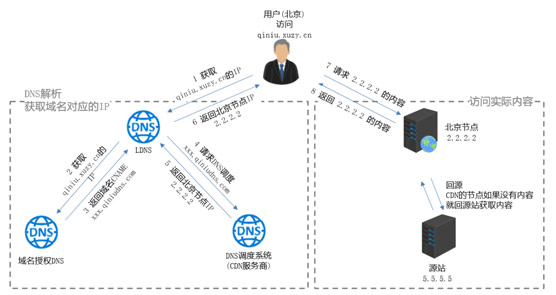
Java多级缓存是为了解决什么的?
前言 提到缓存,想必每一位软件工程师都不陌生,它是目前架构设计中提高性能最直接的方式。 缓存技术存在于应用场景的方方面面。从网站提高性能的角度分析,缓存可以放在浏览器,可以放在反向代理服务器,还可以放…...

Prompt Tuning、P-Tuning、Prefix Tuning的区别
一、Prompt Tuning、P-Tuning、Prefix Tuning的区别 1. Prompt Tuning(提示调优) 核心思想:固定预训练模型参数,仅学习额外的连续提示向量(通常是嵌入层的一部分)。实现方式:在输入文本前添加可训练的连续向量(软提示),模型只更新这些提示参数。优势:参数量少(仅提…...

《Qt C++ 与 OpenCV:解锁视频播放程序设计的奥秘》
引言:探索视频播放程序设计之旅 在当今数字化时代,多媒体应用已渗透到我们生活的方方面面,从日常的视频娱乐到专业的视频监控、视频会议系统,视频播放程序作为多媒体应用的核心组成部分,扮演着至关重要的角色。无论是在个人电脑、移动设备还是智能电视等平台上,用户都期望…...

聊聊 Pulsar:Producer 源码解析
一、前言 Apache Pulsar 是一个企业级的开源分布式消息传递平台,以其高性能、可扩展性和存储计算分离架构在消息队列和流处理领域独树一帜。在 Pulsar 的核心架构中,Producer(生产者) 是连接客户端应用与消息队列的第一步。生产者…...

DIY|Mac 搭建 ESP-IDF 开发环境及编译小智 AI
前一阵子在百度 AI 开发者大会上,看到基于小智 AI DIY 玩具的演示,感觉有点意思,想着自己也来试试。 如果只是想烧录现成的固件,乐鑫官方除了提供了 Windows 版本的 Flash 下载工具 之外,还提供了基于网页版的 ESP LA…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一)
宇树机器人多姿态起立控制强化学习框架论文解析 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一) 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化…...

PL0语法,分析器实现!
简介 PL/0 是一种简单的编程语言,通常用于教学编译原理。它的语法结构清晰,功能包括常量定义、变量声明、过程(子程序)定义以及基本的控制结构(如条件语句和循环语句)。 PL/0 语法规范 PL/0 是一种教学用的小型编程语言,由 Niklaus Wirth 设计,用于展示编译原理的核…...

Docker拉取MySQL后数据库连接失败的解决方案
在使用Docker部署MySQL时,拉取并启动容器后,有时可能会遇到数据库连接失败的问题。这种问题可能由多种原因导致,包括配置错误、网络设置问题、权限问题等。本文将分析可能的原因,并提供解决方案。 一、确认MySQL容器的运行状态 …...

es6+和css3新增的特性有哪些
一:ECMAScript 新特性(ES6) ES6 (2015) - 革命性更新 1,记住的方法,从一个方法里面用到了哪些技术 1,let /const块级作用域声明2,**默认参数**:函数参数可以设置默认值。3&#x…...

五、jmeter脚本参数化
目录 1、脚本参数化 1.1 用户定义的变量 1.1.1 添加及引用方式 1.1.2 测试得出用户定义变量的特点 1.2 用户参数 1.2.1 概念 1.2.2 位置不同效果不同 1.2.3、用户参数的勾选框 - 每次迭代更新一次 总结用户定义的变量、用户参数 1.3 csv数据文件参数化 1、脚本参数化 …...

python基础语法Ⅰ
python基础语法Ⅰ 常量和表达式变量是什么变量的语法1.定义变量使用变量 变量的类型1.整数2.浮点数(小数)3.字符串4.布尔5.其他 动态类型特征注释注释是什么注释的语法1.行注释2.文档字符串 注释的规范 常量和表达式 我们可以把python当作一个计算器,来进行一些算术…...
