数据分析思维(六)|循环/闭环思维
循环/闭环思维
1、概念
在很多的分析场景下,我们需要按照一套流程反复分析,而不是进行一次性的分析,也就是说这套流程的结果会成为该流程的新一次输入,从而形成一个闭环,此时的分析思维我们称之为循环/闭环思维。
常见的闭环思维如下:
- 业务流程闭环
- 生命周期闭环
- 产品功能使用闭环
- 市场推广策略闭环
本文列举常见的PDCA循环进行该思维的讲解。
2、PDCA循环
概念
PDCA循环法的概念是在管理学中被提出的,该方法的目的就是用于对当前的任务(事物)进行优化,达到精益求精的效果,简单的说就是按照一套标准的流程去不断完善当前的任务,得到最好的解决方案。
PDCA的组成如下:
- P(Plan)-计划
- D(D0)-执行
- C(Check)-检查
- A(Act)-处理
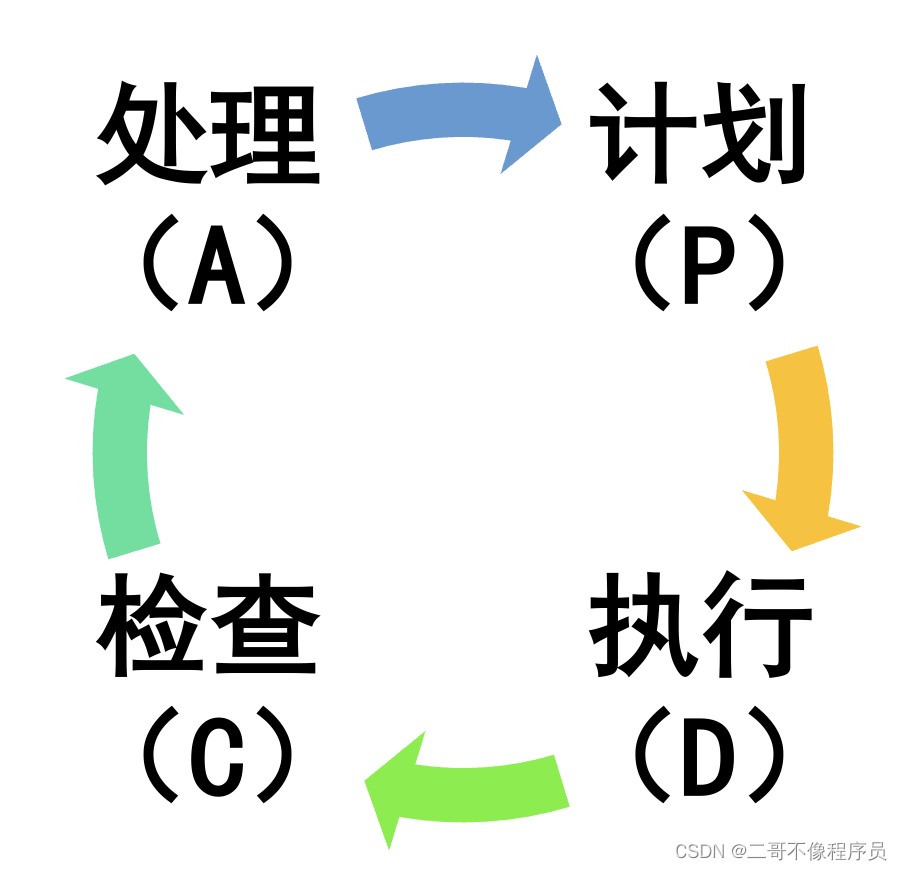
流程
PDCA的概念我们不难理解,那作为一个可以应用于很多场景的方法而言,我们应该如何去使用呢,下面通过8个步骤来了解一下一个闭环内的PDCA流程。
| 阶段 | 步骤 |
|---|---|
| P | 1、分析现状,找出问题 |
| 2、分析问题产生的各种原因 | |
| 3、找出主要的影响因素 | |
| 4、针对主要影响因素,制定计划 | |
| D | 5、执行计划 |
| C | 6、计划执行的结果展示 |
| A | 7、复盘总结,制定标准 |
| 8、问题总结,处理下一个问题 |
总结
上述的8个步骤不难理解,我们通过一次PDCA循环解决了一个重要问题,接下来的循环就是去解决该问题的分支或者第二重要的问题了,PDCA不会死板的要求我们一定按照某种顺序去解决,当问题有大有小时我们就先解决大问题,当问题有次序关系时,我们就按顺序进行解决即可。
除了PDCA循环之外,其他的闭环场景(产品功能闭环、用户生命周期闭环)等也适用于上述解决问题的思想。
3、举个例子
大家都参加过各大电商每年推出的618、双十一之类的活动,对于这类的运营活动推进我们就可以使用PDCA闭环进行分析,下面举一个简单的运营活动的PDCA闭环分析。
- 问题
某次运营活动,A公司想要实现1000W的GMV,应该如何设计活动?如何思考?
- 分析(P)
- 问题:如何实现1000W的GMV
- 拆分:公司现GMV来源可分为两部分人群——新用户/老用户
- 影响因素:新用户(品牌/产品曝光)|老用户(复购能力)
- 计划:新用户(打广告)|老用户(复购活动)
- 执行(D)
- 设计相应的广告及老用户的复购活动进行执行
- 检查(C)
- 活动进行一半,新用户完成40%,老用户完成60%
- 总结(A)
- 复盘:新用户点击广告的频率不高
- 调整:提高广告点击率(下一个PDCA)
- 总结:记录本次问题产生的原因(用作后续活动的经验)
上述的过程就是按照第2节中我们所提出的步骤进行拆分得到的结果,使用PDCA闭环,不难发现我们得到的条理非常清晰,但是也暴露出PDCA循环容易让我们产生惯性思维而缺少一些角度的思考的缺点。总体来说,模型就是一个基础,后续在不同的场景下我们可以进行适当的调整,最终形成属于自己的闭环思维即可。
相关文章:

数据分析思维(六)|循环/闭环思维
循环/闭环思维 1、概念 在很多的分析场景下,我们需要按照一套流程反复分析,而不是进行一次性的分析,也就是说这套流程的结果会成为该流程的新一次输入,从而形成一个闭环,此时的分析思维我们称之为循环/闭环思维。 常…...

C++:类和对象(下)
文章目录1 再谈构造函数1.1 构造函数体赋值1.2 初始化列表1.3 explicit关键字2 static成员2.1 概念2.2 特性3 友元3.1 友元函数(流插入(<<)及流提取(>>)运算符重载)3.2 友元类4 内部类5 匿名对…...

ASP.NET Core MVC 项目 AOP之IResultFilter和IAsyncResultFilter
目录 一:说明 二:IActionFilter同步 三:IAsyncActionFilter异步 一:说明 IResultFilter同步过滤器与IAsyncResultFilter异步过滤器常常被用作于渲染视图或处理结果。 IResultFilter同步过滤器执行顺序: 1:执行控制器中的构造函数,实例化控制器 2:执行具体的Acti…...
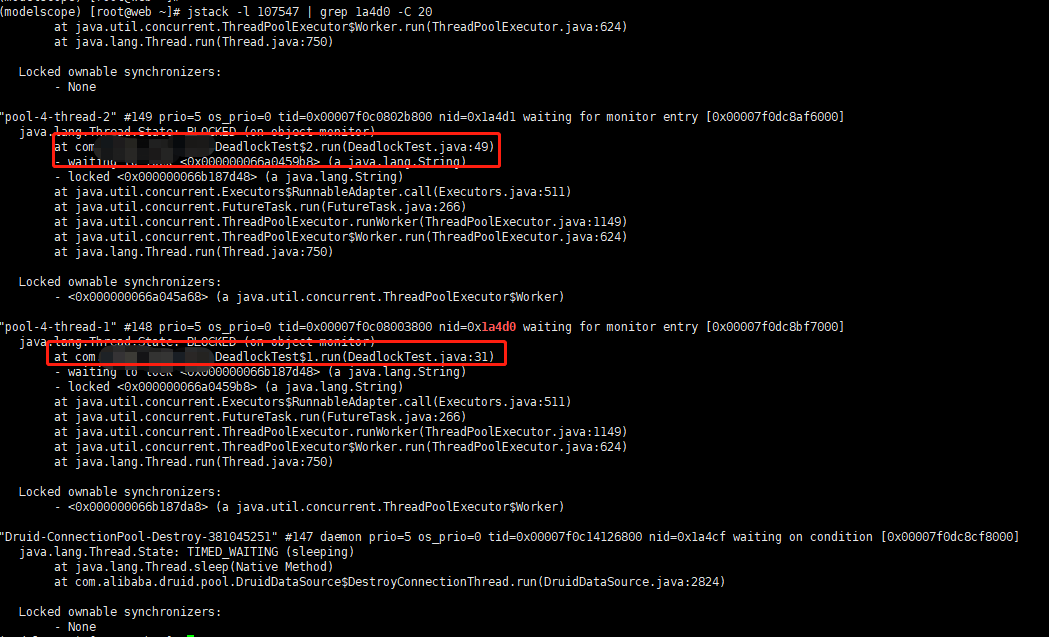
jstack排查cpu占用高[复习]
这样就可以看到占用CPU高的代码位置。 总结:就是先查到占用高的应用和具体的线程,然后根据线程到堆积信息查找即可。 不过堆栈信息非十进制,需提前把线程号转为十六进制。 这样就可以看到占用CPU高的代码位置。 总结:就是先查到…...
网络安全-Pyhton环境搭建
网络安全-Pyhton环境搭建 https://www.kali.org/get-kali/#kali-installer-images—kali官网下载地址 python这个东东呢 是目前来说最简单,方便的开源的脚本语言 广泛用于Web开发,AI,网站开发等领域 python要装2和3 为什么要安装两个版本…...

SpringBoot Mybatis 分页实战
pageInfo的属性 pageNum:当前页 pageSize:页面数据量 startRow:当前页首条数据为总数据的第几条 endRow:当前页最后一条数据为总数据的第几条 total:总数据量 pages:总页面数 listPage{}结果集 reasonable …...

计算机断层扫描结肠镜和全自动骨密度仪在一次检查中的可行性
计算机断层扫描结肠镜和全自动骨密度仪在一次检查中的可行性 Feasibility of Simultaneous Computed Tomographic Colonography and Fully Automated Bone Mineral Densitometry in a Single Examination 简单总结: 数据:患者的结肠镜检查和腹部CT检查…...
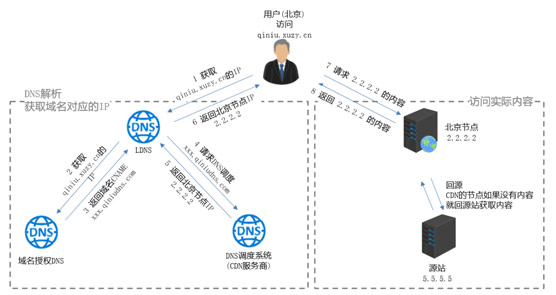
Java多级缓存是为了解决什么的?
前言 提到缓存,想必每一位软件工程师都不陌生,它是目前架构设计中提高性能最直接的方式。 缓存技术存在于应用场景的方方面面。从网站提高性能的角度分析,缓存可以放在浏览器,可以放在反向代理服务器,还可以放…...

MongoDB--》索引的了解及具体操作
目录 索引—index 索引的类型 索引的管理操作 索引的使用 索引—index 使用索引的原因:索引支持在MongoDB中高效地执行查询。如果没有索引,MongoDB必须执行全集合扫描,即扫描集合中的每个文档,以选择与查询语句匹配的文档。这…...
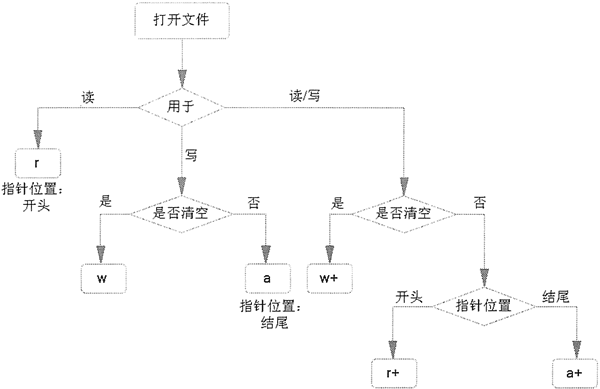
Python open()函数详解:打开指定文件
在 Python 中,如果想要操作文件,首先需要创建或者打开指定的文件,并创建一个文件对象,而这些工作可以通过内置的 open() 函数实现。open() 函数用于创建或打开指定文件,该函数的常用语法格式如下:file ope…...

CentOS Stream 9尝鲜安装教程
作者:IT圈黎俊杰 一、下载CentOS Stream 9安装介质 在CentOS官网可以下载到CentOS Stream 9的安装介质,正面列出ISO介质的下载链接地址: https://download.cf.centos.org/9-stream/BaseOS/x86_64/iso/CentOS-Stream-9-20221019.0-x86_64-dv…...

Ambire AdEx 2023 年路线图
Ambire AdEx 是为简化 web3 显示广告而建立的,领先于时代。到 2023 年,它将专注于服务用户需求,同时保持其作为区块链隐私解决方案的核心,反对传统的数字广告模式。 回顾 2022 年 2022 年,AdEx 网络处理了超过 1 亿次展…...
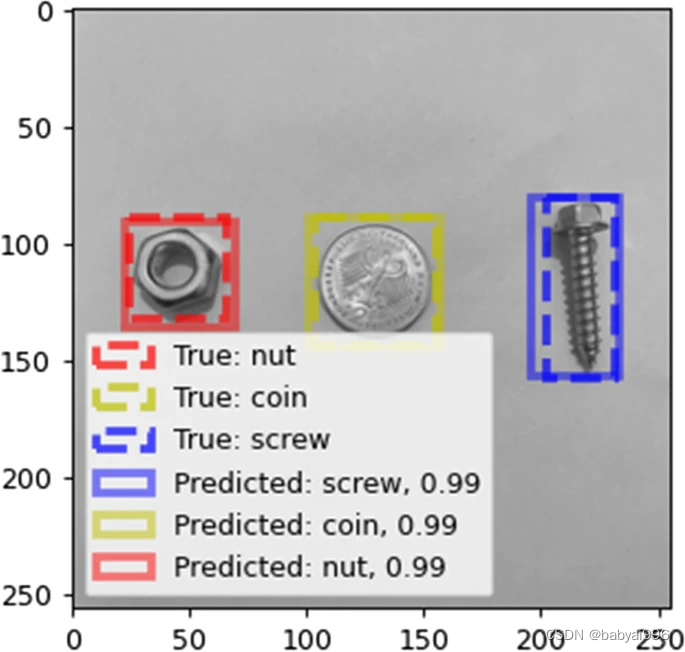
两种特征提取方法与深度学习方法对比的小型金属物体分类分析研究
本文讨论了用于对包括螺丝、螺母、钥匙和硬币在内的小型金属物体进行分类的两种特征提取方法的效率:定向梯度直方图 (HOG) 和局部二进制模式 (LBP)。首先提取标记图像的所需特征并以特征矩阵的形式保存。使用三种不同的分类方法(非参数 K 最近邻算法、支…...
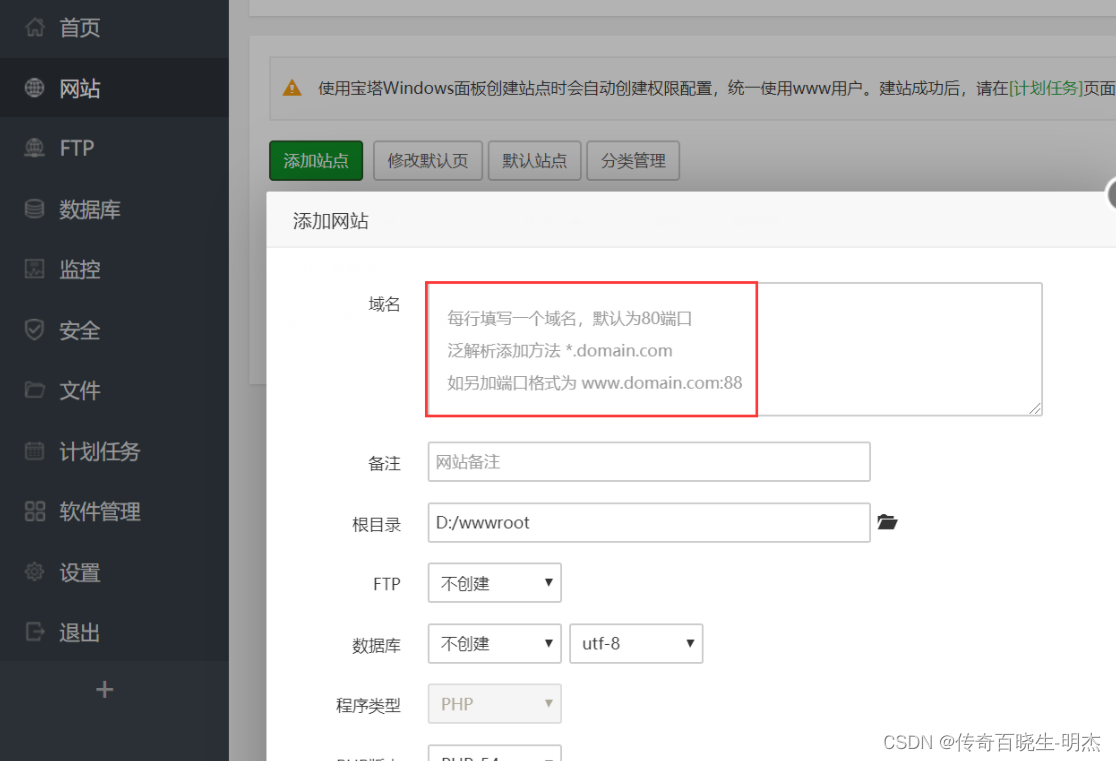
传奇私服搭建网站的几种方法
搭建网站的几种方法:一些人,连简单的搭建网站都不会,还要请技术帮忙,真是牛B,这里简单介绍下几种办法一:2003系统下,直接使用IIS,这个太简单了,桌面上就有IIS,…...
- 各类clock的注册)
i.MX8MP平台开发分享(clock篇)- 各类clock的注册
专栏目录:专栏目录传送门 平台内核i.MX8MP5.15.71文章目录 1、关键数据结构1.1 clk_hw1.2 clk_hw_onecell_data2.一个clk的注册过程2.1 fixed clk2.2 pll14xx2.3 fixed factor2.4 mux2.5 composite2.6 gate1、关键数据结构 1.1 clk_hw clk_hw是描述一个时钟信息的最小单元。…...
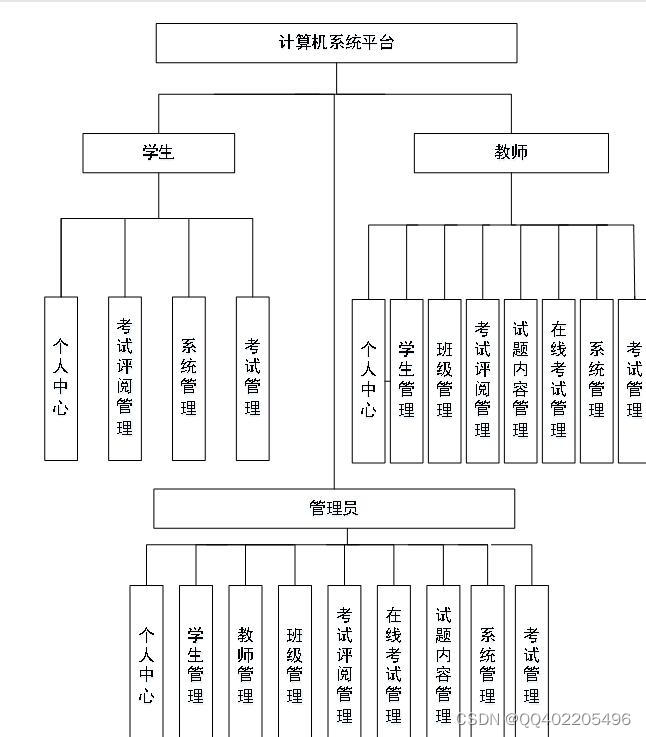
java ssm计算机系统在线考试平台idea
本系统主要包括以下功能模块学生、教师、班级、考试评阅、在线考试、试题内容、考试等模块,通过这些模块的实现能够基本满足日常计算机系统平台的操作。 本文着重阐述了计算机系统平台的分析、设计与实现,首先介绍开发系统和环境配置、数据库的设计&…...

C语言(字符串函数)
这章的内容记得引用<string.h>头文件 目录 1.strlen() 2.strcat() 3.strncat() 4.strcmp() 5.strncmp() 6.strcpy() 7.strncpy() 8.sprintf() 8.strchr() 9.strpbrk() 10.strrchr() 11.strstr() 1.strlen() 用于统计字符串的…...
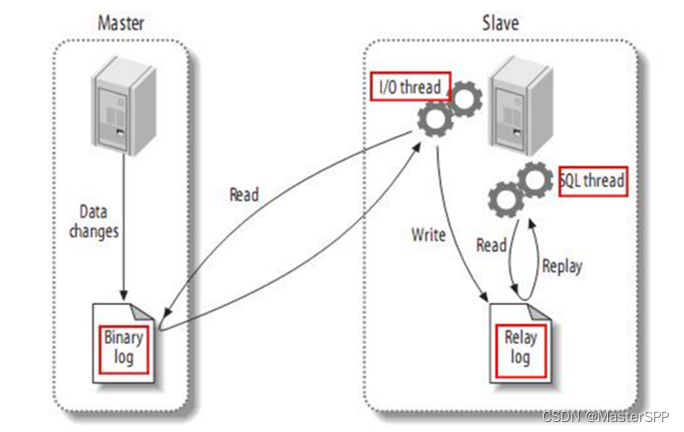
Maxwell工作流程详解
要介绍maxwell的工作原理,首先需要讲一下mysql主从复制的原理 mysql主从复制原理: 如上图,左边是master主节点,右边是slave从节点 工作流程: 1.往主节点mysql的数据库中写入数据,产生数据变化,…...
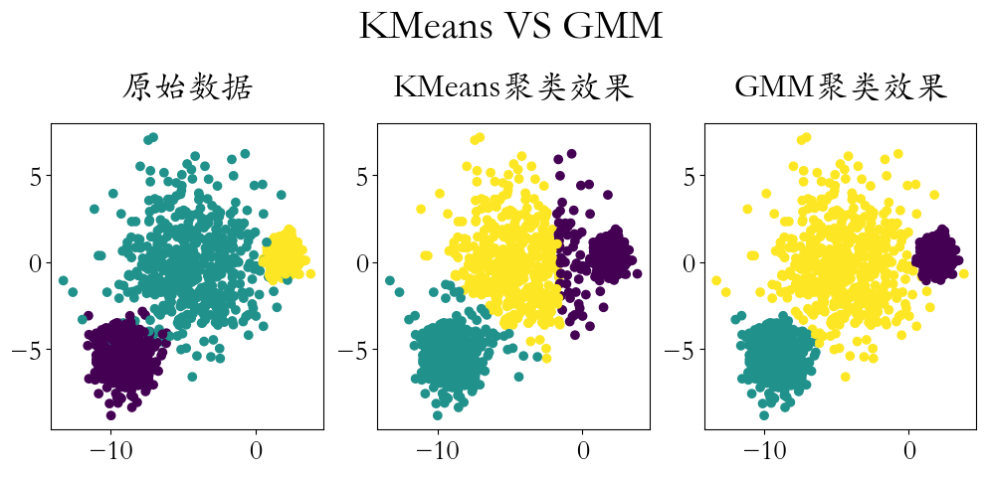
13- EM算法与GMM高斯混合 (聚类算法) (算法)
最大期望算法(EM算法) ,曾入选“数据挖掘十大算法”中,是最常见的隐变量估计方法,在机器学习中有极为广泛的用途,例如常被用来学习高斯混合模型的参数。EM算法是在概率模型中寻找参数最大似然估计或者最大后验估计的算法ÿ…...
| 刷完获取OD招聘渠道)
【新】华为OD机试 - 二叉树层次遍历(Python)| 刷完获取OD招聘渠道
二叉树层次遍历 题目 有一棵二叉树 每一个节点用一个大写字母标识 最多26个节点 现有两组字母 分别表示后序遍历(左孩子指向右孩子指向父节点) 和中序遍历(左孩子指向父节点指向右孩子) 请输出层次遍历的结果 输入 输入为两个字符串 分别为二叉树的后序遍历和中序遍历结…...

未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?
编辑:陈萍萍的公主一点人工一点智能 未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?RWM通过双自回归机制有效解决了复合误差、部分可观测性和随机动力学等关键挑战,在不依赖领域特定归纳偏见的条件下实现了卓越的预测准…...

AI-调查研究-01-正念冥想有用吗?对健康的影响及科学指南
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

idea大量爆红问题解决
问题描述 在学习和工作中,idea是程序员不可缺少的一个工具,但是突然在有些时候就会出现大量爆红的问题,发现无法跳转,无论是关机重启或者是替换root都无法解决 就是如上所展示的问题,但是程序依然可以启动。 问题解决…...

vscode里如何用git
打开vs终端执行如下: 1 初始化 Git 仓库(如果尚未初始化) git init 2 添加文件到 Git 仓库 git add . 3 使用 git commit 命令来提交你的更改。确保在提交时加上一个有用的消息。 git commit -m "备注信息" 4 …...

SkyWalking 10.2.0 SWCK 配置过程
SkyWalking 10.2.0 & SWCK 配置过程 skywalking oap-server & ui 使用Docker安装在K8S集群以外,K8S集群中的微服务使用initContainer按命名空间将skywalking-java-agent注入到业务容器中。 SWCK有整套的解决方案,全安装在K8S群集中。 具体可参…...

蓝桥杯 2024 15届国赛 A组 儿童节快乐
P10576 [蓝桥杯 2024 国 A] 儿童节快乐 题目描述 五彩斑斓的气球在蓝天下悠然飘荡,轻快的音乐在耳边持续回荡,小朋友们手牵着手一同畅快欢笑。在这样一片安乐祥和的氛围下,六一来了。 今天是六一儿童节,小蓝老师为了让大家在节…...
)
GitHub 趋势日报 (2025年06月08日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 884 cognee 566 dify 414 HumanSystemOptimization 414 omni-tools 321 note-gen …...

汇编常见指令
汇编常见指令 一、数据传送指令 指令功能示例说明MOV数据传送MOV EAX, 10将立即数 10 送入 EAXMOV [EBX], EAX将 EAX 值存入 EBX 指向的内存LEA加载有效地址LEA EAX, [EBX4]将 EBX4 的地址存入 EAX(不访问内存)XCHG交换数据XCHG EAX, EBX交换 EAX 和 EB…...
)
是否存在路径(FIFOBB算法)
题目描述 一个具有 n 个顶点e条边的无向图,该图顶点的编号依次为0到n-1且不存在顶点与自身相连的边。请使用FIFOBB算法编写程序,确定是否存在从顶点 source到顶点 destination的路径。 输入 第一行两个整数,分别表示n 和 e 的值(1…...

佰力博科技与您探讨热释电测量的几种方法
热释电的测量主要涉及热释电系数的测定,这是表征热释电材料性能的重要参数。热释电系数的测量方法主要包括静态法、动态法和积分电荷法。其中,积分电荷法最为常用,其原理是通过测量在电容器上积累的热释电电荷,从而确定热释电系数…...
