13- EM算法与GMM高斯混合 (聚类算法) (算法)
-
最大期望算法(EM算法) ,曾入选“数据挖掘十大算法”中,是最常见的隐变量估计方法,在机器学习中有极为广泛的用途,例如常被用来学习高斯混合模型的参数。EM算法是在概率模型中寻找参数最大似然估计或者最大后验估计的算法,其中概率模型依赖于无法观测的隐性变量。通常分两步实现:
-
第一步是计算期望(E),利用对隐藏变量的现有估计值,计算其最大似然估计值;
-
第二步是最大化(M),最大化在E步上求得的最大似然值来计算参数的值。M步上找到的参数估计值被用于下一个E步计算中,这个过程不断交替进行。
-
-
GMM (高斯混合模型) 是一个用于聚类的概率模型,其使用了EM算法进行迭代计算,高斯混合模型假设每个簇的数据都是符合高斯分布(又叫正态分布)的,当前数据呈现的分布就是各个簇的高斯分布叠加在一起的结果。
from sklearn.mixture import GaussianMixture
# GMM高斯混合模型聚类
gmm = GaussianMixture(n_components=3)
y_ = gmm.fit_predict(X)1、EM算法简介
1.1、EM算法概述
最大期望算法(Expectation-maximization algorithm,又译为期望最大化算法),曾入选“数据挖掘十大算法”中,可见EM算法在机器学习、数据挖掘中的影响力。EM算法是最常见的隐变量估计方法,在机器学习中有极为广泛的用途,例如常被用来学习高斯混合模型(Gaussian mixture model,简称GMM)的参数。
EM算法是在概率模型中寻找参数最大似然估计或者最大后验估计的算法,其中概率模型依赖于无法观测的隐性变量。
1.2、EM算法流程
EM算法是一种迭代优化策略,由于它的计算方法中每一次迭代都分两步,其中一个为期望步(E步),另一个为极大步(M步),所以算法被称为EM算法(Expectation-Maximization Algorithm)。
最大期望算法经过两个步骤交替进行计算:
-
第一步是计算期望(E),利用对隐藏变量的现有估计值,计算其最大似然估计值;
-
第二步是最大化(M),最大化在E步上求得的最大似然值来计算参数的值。M步上找到的参数估计值被用于下一个E步计算中,这个过程不断交替进行。
2、极大似然
2.1、似然函数
什么是极大似然,首先来看一下似然函数, 在数理统计学中,似然函数是一种关于统计模型中的参数的函数,表示模型参数中的似然性。“似然性”与“或然性”或“概率”意思相近,都是指某种事件发生的可能性。
2.2、极大似然
极大似然,也叫最大似然,就是似然函数的最大值!而极大似然就相当于最大可能的意思。
比如一位同学和一位猎人一起外出打猎,一只野兔从前方窜过。只听一声枪响,野兔应声到下,如果要你推测,这一发命中的子弹是谁打的?你就会想,只发一枪便打中,由于猎人命中的概率一般大于那位同学命中的概率,从而推断出这一枪应该是猎人射中的。这个例子所作的推断就体现了最大似然法的基本思想。
2.3、最大似然示例计算
最大似然估计 (maximum likelihood estimation, MLE) 一种重要而普遍的求估计量的方法。最大似然估计明确地使用概率模型,其目标是寻找能够以较高概率产生观察数据的系统发生树。最大似然估计是一类完全基于统计的系统发生树重建方法的代表。
2.4、极大似然步骤
-
写出似然函数;
-
对似然函数取对数,并整理;
-
求导数,令导数为0,得到似然方程;
-
解似然方程,得到的参数即为所求;
3、EM算法入门
3.1、问题描述
我们需要调查学校的男生和女生的身高分布 ,我们抽取100个男生和100个女生,将他们按照性别划分为两组。然后,统计抽样身高数据。我们知道他们的身高服从正态分布(自然属性一般服从正态分布),但分布的均值 和方差 是未知的,就是要估计的参数。
问题:我们知道样本所服从的概率分布模型和一些样本,我们需要求解该模型的参数。
-
我们已知的条件有两个:
-
样本服从的分布模型(正态分布)
-
随机抽取的样本。
-
-
我们需要求解模型的参数。
根据已知条件,通过极大似然估计,求出未知参数。总的来说:极大似然估计就是用来估计模型参数的统计学方法。
多数情况下,我们是根据已知条件来推算结果,而极大似然估计是已知结果,寻求使该结果出现的可能性最大的条件,以此作为估计值。
4、EM算法进阶
4.1、聚类问题
我们目前有100个男生和100个女生的身高,但是我们不知道这200个数据中哪个是男生的身高,哪个是女生的身高,即抽取得到的每个样本都不知道是从哪个分布中抽取的。
这个时候,对于每个样本,就有两个未知量需要估计:
-
这个身高数据是来自于男生数据集合还是来自于女生?(聚类问题)
-
男生、女生身高数据集的正态分布的参数分别是多少?
4.2、解决方案
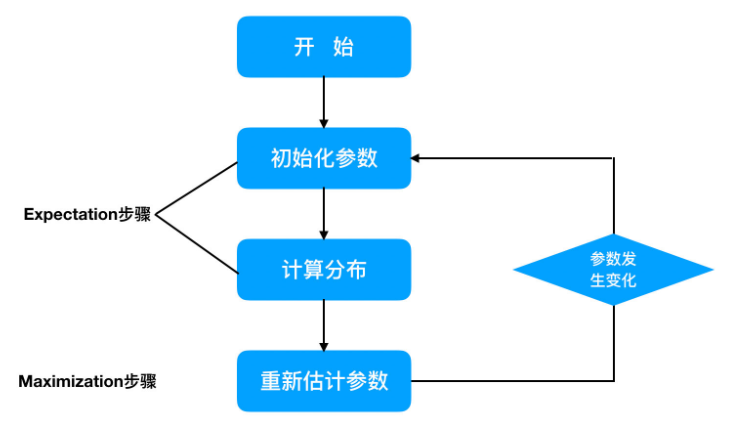
对具体的男女生身高问题使用EM算法求解流程如下:
-
初始化参数:先初始化男生身高的正态分布的参数:如均值=1.64,方差=6.0;
-
计算分布:计算每一个人更可能属于男生分布或者女生分布;
-
重新估计参数:通过分为男生的n个人来重新估计男生身高分布的参数(最大似然估计),女生分布也按照相同的方式估计出来,更新分布。
-
这时候两个分布的概率也变了,然后重复步骤2~3,直到参数不发生变化为止
5、Jensen不等式
设f是定义域为实数的函数,如果对所有的实数x,f(x)的二阶导数都大于0,那么f是凸函数。
Jensen不等式定义如下:
如果f是凸函数,X是随机变量,那么:。当且仅当X是常量时,该式取等号。其中,E(X)表示X的数学期望。
注:Jensen不等式应用于凹函数时,不等号方向反向。当且仅当x是常量时,该不等式取等号。
总结如下:
- 如果f是凸函数,X是随机变量,那么:E[f(X)]>=f(E[X]),通俗的说法是函数的期望大于等于期望的函数。
- 特别地,如果f是严格凸函数,当且仅当P(X = EX) = 1,即X是常量时,上式取等号,即E[f(X)] = f(EX)。
6、EM算法公式推导
暂不深入研究
7、GMM高斯混合模型 (默认数据属于正太分布)
高斯混合模型是一个用于聚类的概率模型,其使用了EM算法进行迭代计算,高斯混合模型假设每个簇的数据都是符合高斯分布(又叫正态分布)的,当前数据呈现的分布就是各个簇的高斯分布叠加在一起的结果。
高斯分布的概率密度函数为:
GMM算法,是EM算法的一种落地实现方式。
GMM算法示例
import numpy as np
from sklearn import datasets
import matplotlib.pyplot as plt
from sklearn.mixture import GaussianMixture
from sklearn.cluster import KMeans
# 创建数据,并可视化
X,y = datasets.make_blobs(n_samples=1500,cluster_std=[1.0, 2.5, 0.5],random_state=170)
plt.figure(figsize=(12,4))
plt.rcParams['font.family'] = 'STKaiti'
plt.rcParams['font.size'] = 20
plt.subplot(1,3,1)
plt.scatter(X[:,0],X[:,1],c = y)
plt.title('原始数据',pad = 20)# Kmeans聚类
kmeans = KMeans(3)
kmeans.fit(X)
y_ = kmeans.predict(X)
plt.subplot(1,3,2)
plt.scatter(X[:,0],X[:,1],c = y_)
plt.title('KMeans聚类效果',pad = 20)# GMM高斯混合模型聚类
gmm = GaussianMixture(n_components=3)
y_ = gmm.fit_predict(X)
plt.subplot(1,3,3)
plt.scatter(X[:,0],X[:,1],c = y_)
plt.title('GMM聚类效果',pad = 20)plt.figtext(x = 0.51,y = 1.1,s = 'KMeans VS GMM',ha = 'center',fontsize = 30)
plt.savefig('./GMM高斯混合模型.png',dpi = 200)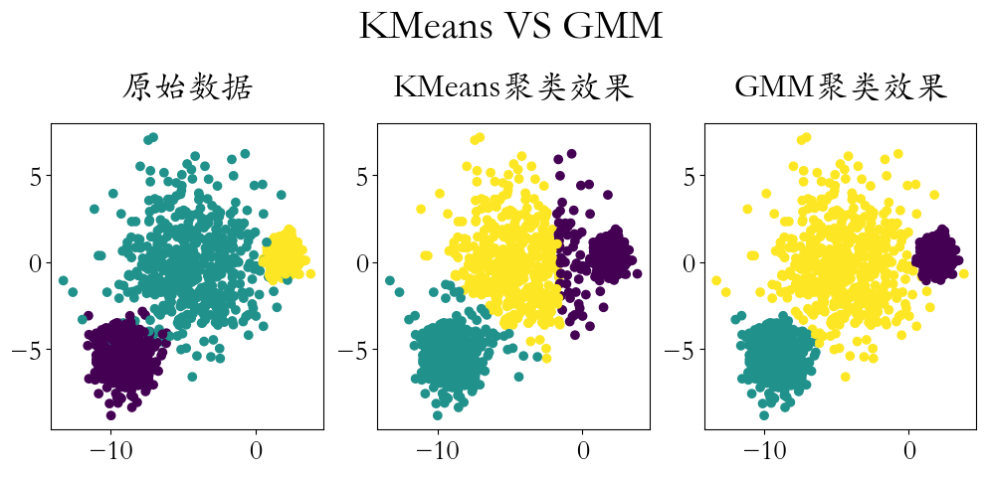
相关文章:

13- EM算法与GMM高斯混合 (聚类算法) (算法)
最大期望算法(EM算法) ,曾入选“数据挖掘十大算法”中,是最常见的隐变量估计方法,在机器学习中有极为广泛的用途,例如常被用来学习高斯混合模型的参数。EM算法是在概率模型中寻找参数最大似然估计或者最大后验估计的算法ÿ…...
| 刷完获取OD招聘渠道)
【新】华为OD机试 - 二叉树层次遍历(Python)| 刷完获取OD招聘渠道
二叉树层次遍历 题目 有一棵二叉树 每一个节点用一个大写字母标识 最多26个节点 现有两组字母 分别表示后序遍历(左孩子指向右孩子指向父节点) 和中序遍历(左孩子指向父节点指向右孩子) 请输出层次遍历的结果 输入 输入为两个字符串 分别为二叉树的后序遍历和中序遍历结…...
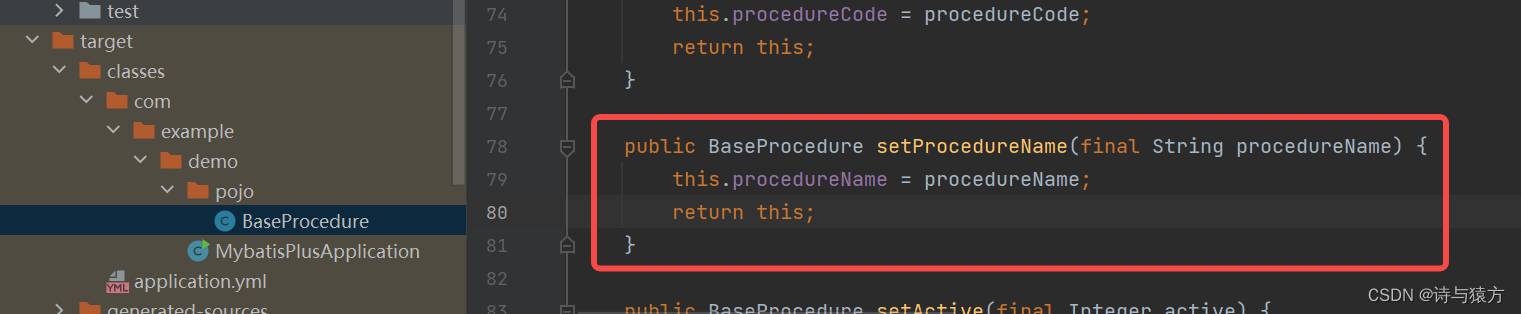
工作记录------@Accessors(chain = true)引起的BUG,Excel导入时获取不到值
工作记录------Accessors(chain true)引起的BUG,Excel导入时获取不到值 如题所示 背景:在进行文件excel文件导入时,发现实体类获取到的属性值都为null。 框架:com.alibaba.excel 2.2.0的版本。 结论:首先说下结论 如…...
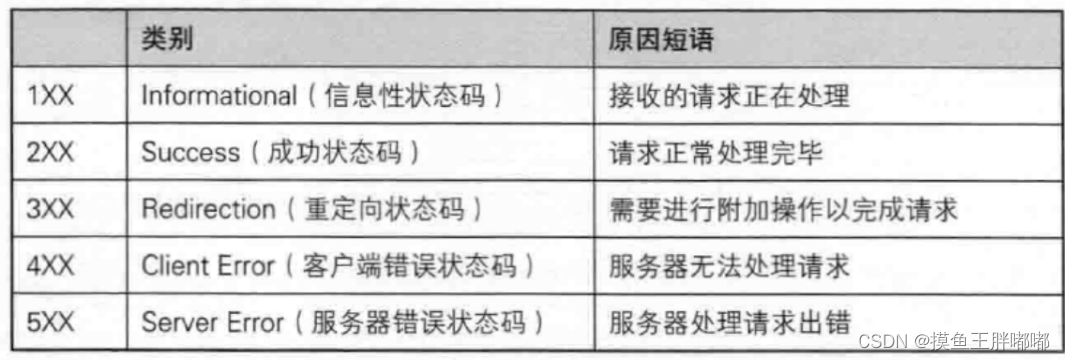
JavaEE-HTTP协议(二)
目录HTTP请求的方法GET方法POST 方法其他方法“报头”User-AgentRefererCookieHTTP响应200 OK404 Not Found403 Forbidden405 Method Not Allowed500 Internal Server Error504 Gateway Timeout302 Move temporarily301 Moved PermanentlyHTTP请求的方法 GET方法 GET 是最常用…...

代理的基本原理和多线程的基本原理
目录爬虫代理常见代理多线程并发和并行Python中的多进程和多线程爬虫时我们不到一杯茶的功夫就出现了403.打开网页一看会说您的IP访问频率太高,出现这种情况是因为网站采取了一些反爬虫措施,限制某个IP在一定时间内的请求次数,如果超过一定的…...

T38,数的递归
描述 输入一棵节点数为 n 二叉树,判断该二叉树是否是平衡二叉树。 在这里,我们只需要考虑其平衡性,不需要考虑其是不是排序二叉树 平衡二叉树(Balanced Binary Tree),具有以下性质:它是一棵空…...

QT+ OpenGL 变换
文章目录QT OpenGL变换向量的运算矩阵矩阵与向量相乘代码实现QT OpenGL 本篇完整工程见gitee:QTOpenGL 对应点的tag,由turbolove提供技术支持,您可以关注博主或者私信博主。 变换 我们需要改变物体的位置 现有解决办法(每一帧,…...
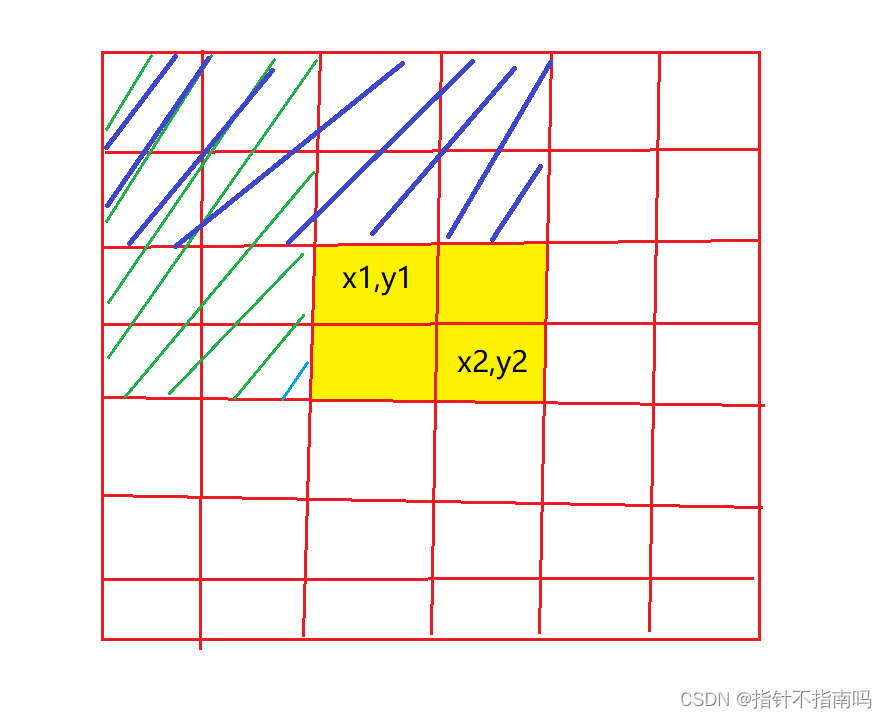
【算法】前缀和
作者:指针不指南吗 专栏:算法篇 🐾要学会在纸上打草稿,这个很重要🐾 文章目录1.什么是前缀和?2.怎么求前缀和?3.前缀和有什么用?4.进阶二维:矩阵和前缀和 主打一个记公式 1.什么是前…...
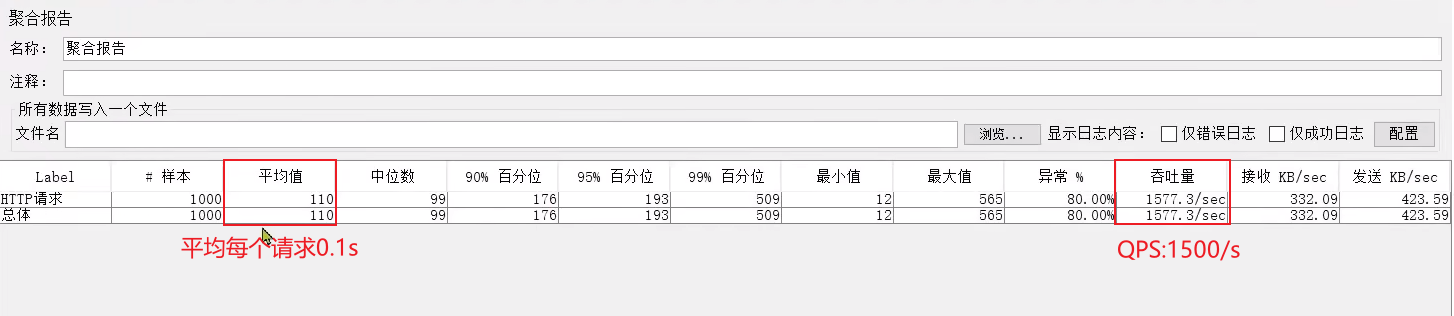
《Redis实战篇》七、Redis消息队列
7.1 Redis消息队列-认识消息队列 什么是消息队列:字面意思就是存放消息的队列。最简单的消息队列模型包括3个角色: 消息队列:存储和管理消息,也被称为消息代理(Message Broker)生产者:发送消息…...

android组件化
学习流程:1.开源最佳实践:Android平台页面路由框架ARouter-阿里云开发者社区 (aliyun.com)2.中文ARouter使用API:https://github.com/alibaba/ARouter/blob/master/README_CN.md3.看当前文档后面的代码4.这是通俗易懂的文章:https…...
)
华为OD机试真题Python实现【特异性双端队列】真题+解题思路+代码(20222023)
🔥系列专栏 华为OD机试(Python)真题目录汇总华为OD机试(JAVA)真题目录汇总华为OD机试(C++)真题目录汇总华为OD机试(JavaScript)真题目录汇总文章目录 🔥系列专栏题目输入输出示例一输入输出解题思路核心知识点Python 代码实现代码运行结果版权说明<...

24.架构能力
文章目录24. 架构能力24.1 Competence of Individuals: Duties, Skills, and Knowledge of Architects 个人能力:架构师的职责、技能和知识24.2 Competence of a Software Architecture Organization 软件架构组织的能力24.3 Summary 小结24.4 For Further Reading …...

前端原生 CSS 跑马灯效果,无限轮播(横竖版本,带渐变遮罩,简单实用)
一、横版跑马灯 <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><meta http-equiv"X-UA-Compatible" content"IEedge"><meta name"viewport" content"widthdevice-wid…...
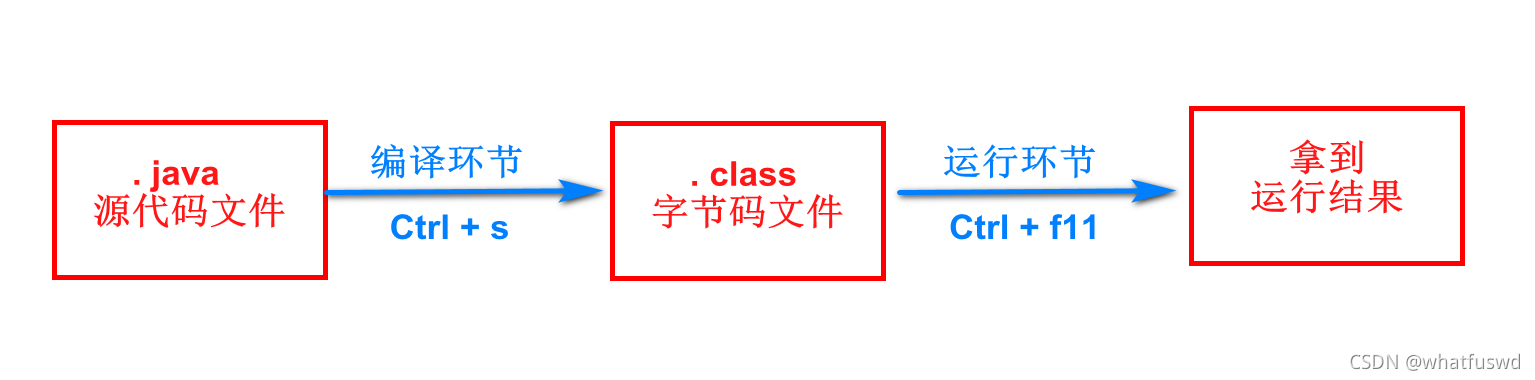
4.8 注解与自定义注解
文章目录1.概述2.注解的分类2.1 JDK注解2.2 元注解2.2.1 Target ElementType…2.2.2 Retention RetentionPolicy…3 自定义注解1.概述 在注解刚出现时,曾受到过好多程序员的鄙夷,觉得这就是多此一举的操作; 但随着时间的推移,越…...

webpack 的热更新是如何做到的?原理是什么?
Hot Module Replacement,简称 HMR,在不需要刷新整个页面的同时更新模块,能够提升开发的效率和体验。热更新时只会局部刷新页面上发生了变化的模块,同时可以保留当前页面的状态,比如复选框的选中状态等。 在 webpack 中…...
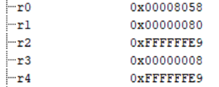
嵌入式ARM设计编程(一) 简单数据搬移
文章和代码已归档至【Github仓库:hardware-tutorial】,需要的朋友们自取。或者公众号【AIShareLab】回复 嵌入式 也可获取。 一、实验目的 熟悉实验开发环境,掌握简单ARM汇编指令的使用方法。 二、实验环境 硬件:PC机 软件&am…...

【Selenium】十分钟手把手带你学会WebDriver API
目录 1、定位元素【8种】 2、操作测试对象 3、添加等待 4、弹窗类型 5、浏览器的操作 6、键盘事件 7、选择框 8、上传文件 1、定位元素【8种】 元素定位是自动化测试的核心,想要去操作一个对象,第一步就是需要我们先去识别这个对象。每个对象就会…...
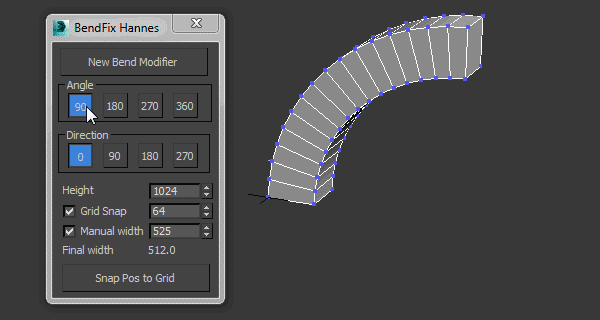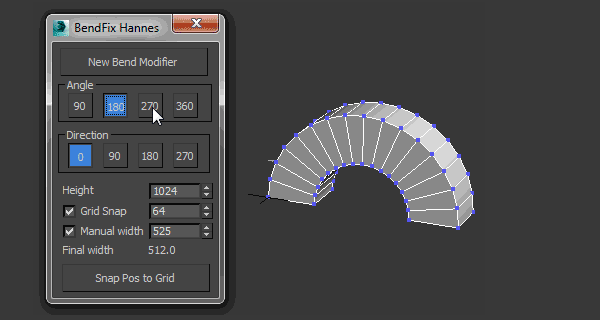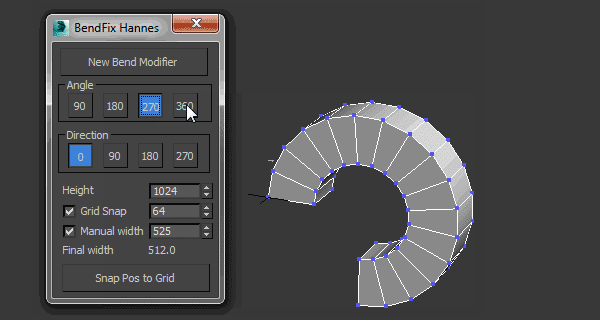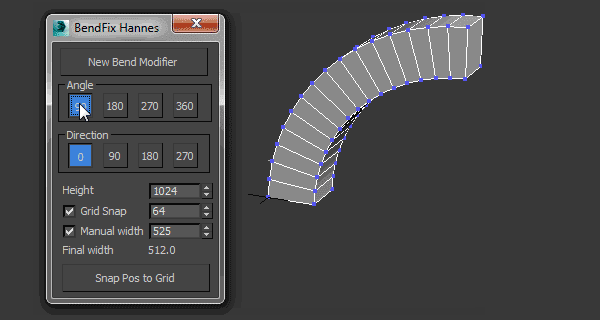
3DMAX高级弯曲插件使用教程
3dMax高级弯曲插件是对3dmax原生“弯曲(Bend)”修改器的一个增强,给用户更多控制弯曲修改器的参数设置,它让用户输入宽度,插件脚本将移动中心以获得正确的宽度。 主要特性: - 使用智能捕捉捕捉到自定义网格…...

前端面试题之性能优化大杂烩
主要内容为下面几大类:移动端、图片、JavaScript、css、html、页面内容、服务器、cookie。 移动端性能优化: 保持单个文件小于25KB 移动网站页面要求下载资源,如果文件过大,会大大减慢页面加载速度。 打包内容为分段multipart文…...
SpringBoot+Vue实现养老智慧服务平台
文末获取源码 开发语言:Java 框架:springboot JDK版本:JDK1.8 服务器:tomcat7 数据库:mysql 5.7/8.0 数据库工具:Navicat11 开发软件:eclipse/myeclipse/idea Maven包:Maven3.3.9 浏…...

JavaSec-RCE
简介 RCE(Remote Code Execution),可以分为:命令注入(Command Injection)、代码注入(Code Injection) 代码注入 1.漏洞场景:Groovy代码注入 Groovy是一种基于JVM的动态语言,语法简洁,支持闭包、动态类型和Java互操作性,…...

iOS 26 携众系统重磅更新,但“苹果智能”仍与国行无缘
美国西海岸的夏天,再次被苹果点燃。一年一度的全球开发者大会 WWDC25 如期而至,这不仅是开发者的盛宴,更是全球数亿苹果用户翘首以盼的科技春晚。今年,苹果依旧为我们带来了全家桶式的系统更新,包括 iOS 26、iPadOS 26…...

模型参数、模型存储精度、参数与显存
模型参数量衡量单位 M:百万(Million) B:十亿(Billion) 1 B 1000 M 1B 1000M 1B1000M 参数存储精度 模型参数是固定的,但是一个参数所表示多少字节不一定,需要看这个参数以什么…...

2025年能源电力系统与流体力学国际会议 (EPSFD 2025)
2025年能源电力系统与流体力学国际会议(EPSFD 2025)将于本年度在美丽的杭州盛大召开。作为全球能源、电力系统以及流体力学领域的顶级盛会,EPSFD 2025旨在为来自世界各地的科学家、工程师和研究人员提供一个展示最新研究成果、分享实践经验及…...

Objective-C常用命名规范总结
【OC】常用命名规范总结 文章目录 【OC】常用命名规范总结1.类名(Class Name)2.协议名(Protocol Name)3.方法名(Method Name)4.属性名(Property Name)5.局部变量/实例变量(Local / Instance Variables&…...

Python实现prophet 理论及参数优化
文章目录 Prophet理论及模型参数介绍Python代码完整实现prophet 添加外部数据进行模型优化 之前初步学习prophet的时候,写过一篇简单实现,后期随着对该模型的深入研究,本次记录涉及到prophet 的公式以及参数调优,从公式可以更直观…...

Robots.txt 文件
什么是robots.txt? robots.txt 是一个位于网站根目录下的文本文件(如:https://example.com/robots.txt),它用于指导网络爬虫(如搜索引擎的蜘蛛程序)如何抓取该网站的内容。这个文件遵循 Robots…...

今日学习:Spring线程池|并发修改异常|链路丢失|登录续期|VIP过期策略|数值类缓存
文章目录 优雅版线程池ThreadPoolTaskExecutor和ThreadPoolTaskExecutor的装饰器并发修改异常并发修改异常简介实现机制设计原因及意义 使用线程池造成的链路丢失问题线程池导致的链路丢失问题发生原因 常见解决方法更好的解决方法设计精妙之处 登录续期登录续期常见实现方式特…...

佰力博科技与您探讨热释电测量的几种方法
热释电的测量主要涉及热释电系数的测定,这是表征热释电材料性能的重要参数。热释电系数的测量方法主要包括静态法、动态法和积分电荷法。其中,积分电荷法最为常用,其原理是通过测量在电容器上积累的热释电电荷,从而确定热释电系数…...

【7色560页】职场可视化逻辑图高级数据分析PPT模版
7种色调职场工作汇报PPT,橙蓝、黑红、红蓝、蓝橙灰、浅蓝、浅绿、深蓝七种色调模版 【7色560页】职场可视化逻辑图高级数据分析PPT模版:职场可视化逻辑图分析PPT模版https://pan.quark.cn/s/78aeabbd92d1...
