QT+ OpenGL 变换
文章目录
- QT+ OpenGL
- 变换
- 向量的运算
- 矩阵
- 矩阵与向量相乘
- 代码实现
QT+ OpenGL
本篇完整工程见gitee:QTOpenGL 对应点的tag,由turbolove提供技术支持,您可以关注博主或者私信博主。
变换
我们需要改变物体的位置
现有解决办法(每一帧,改变顶点位置(所有顶点))
每个顶点使用向量表示,使用矩阵表示对应顶点的操作。
向量的运算
向量是有方向和大小的量
a⃗=(xyz)\vec{a} = \left(\begin{matrix} x \\ y \\z \end{matrix}\right) a=xyz
向量与标量运算
标量(Scalar)只是一个数字(或者说是仅有一个分量的向量)。当把一个向量加/减/乘/除一个标量,我们可以简单的把向量的每个分量分别进行该运算。对于加法来说会像这样:
(123)+x=(1+x2+x3+x)\left(\begin{matrix}1 \\ 2 \\3 \end{matrix}\right) + x = \left(\begin{matrix}1+x \\ 2+x \\3+x \end{matrix}\right) 123+x=1+x2+x3+x
其中的+可以是+,-,·或÷,其中·是乘号。注意-和÷运算时不能颠倒(标量-/÷向量),因为颠倒的运算是没有定义的。
向量取反
−a⃗=−(xyz)=(−x−y−z)-\vec{a} = -\left(\begin{matrix}x \\ y \\z \end{matrix}\right)= \left(\begin{matrix}-x \\ -y \\-z \end{matrix}\right) −a=−xyz=−x−y−z
向量加减
a⃗=(123),b⃗=(123),a⃗+b⃗=(1+12+23+3)=(246)\vec{a} = \left(\begin{matrix}1 \\ 2 \\3 \end{matrix}\right),\vec{b} = \left(\begin{matrix}1 \\ 2 \\3 \end{matrix}\right),\vec{a}+\vec{b} = \left(\begin{matrix}1 + 1\\ 2 + 2 \\3 +3 \end{matrix}\right) = \left(\begin{matrix}2 \\ 4 \\ 6 \end{matrix}\right) a=123,b=123,a+b=1+12+23+3=246
长度
∣v⃗∣=x2+y2(1)|\vec{v}|=\sqrt{x^2+y^2} \tag{1} ∣v∣=x2+y2(1)
向量相乘
- 点乘法: a⃗⋅b⃗\vec{a}\cdot\vec{b}a⋅b
a⃗⋅b⃗=∣a⃗∣⋅∣b⃗∣⋅cosθ\vec{a} \cdot \vec{b} =|\vec{a}|\cdot|\vec{b}|\cdot cos\theta a⋅b=∣a∣⋅∣b∣⋅cosθ
- 叉乘法 : a⃗×b⃗\vec{a}\times\vec{b}a×b
公式如下:
a⃗×b⃗=(AxAyAz)×(BxByBz)=(Ay⋅Bz−Az⋅ByAz⋅Bx−Ax⋅BzAx⋅By−Ay⋅Bx)\vec{a}\times\vec{b} =\left( \begin{matrix} \textcolor{#FF0000}{Ax} \\ \textcolor{#00FF00}{Ay} \\ \textcolor{#0000FF}{Az} \end{matrix}\right) \times \left(\begin{matrix} \textcolor{#FF0000}{Bx} \\ \textcolor{#00FF00}{By} \\ \textcolor{#0000FF}{Bz}\end{matrix}\right) = \left(\begin{matrix}\textcolor{#00FF00}{Ay} \cdot \textcolor{#0000FF}{Bz} - \textcolor{#0000FF}{Az} \cdot \textcolor{#00FF00}{By} \\ \textcolor{#0000FF}{Az} \cdot \textcolor{#FF0000}{Bx} - \textcolor{#FF0000}{Ax} \cdot \textcolor{#0000FF}{Bz} \\ \textcolor{#FF0000}{Ax} \cdot \textcolor{#00FF00}{By} - \textcolor{#00FF00}{Ay} \cdot \textcolor{#FF0000}{Bx }\end{matrix}\right) a×b=AxAyAz×BxByBz=Ay⋅Bz−Az⋅ByAz⋅Bx−Ax⋅BzAx⋅By−Ay⋅Bx
矩阵
一个矩形的数字、符号或者表达式的数组。矩阵中的每一项叫做矩阵的元素
[011110101]\left[\begin{matrix} 0&1&1\\ 1&1&0\\ 1&0&1\\ \end{matrix}\right] 011110101
矩阵的加减
矩阵与标量之间的加减定义如下
[0111]+‾1=[0+‾11+‾11+‾11+‾1]\left[\begin{matrix} 0&1\\ 1&1\\ \end{matrix}\right] \underline+ 1 = \left[\begin{matrix} 0 \underline +1&1\underline + 1\\ 1\underline + 1&1 \underline + 1\\ \end{matrix}\right] [0111]+1=[0+11+11+11+1]
矩阵与矩阵之间的加减就是两个矩阵对应元素的加减运算
[0123]+‾[0123]=[0+‾01+‾12+‾23+‾3]加法=[0246]减法=[0000]\left[\begin{matrix} 0&1\\ 2&3\\ \end{matrix}\right] \underline+ \left[\begin{matrix} 0&1\\ 2&3\\ \end{matrix}\right] = \left[\begin{matrix} 0\underline+0&1\underline+1\\ 2\underline+2&3\underline+3\\ \end{matrix}\right] 加法= \left[\begin{matrix} 0&2\\ 4&6\\ \end{matrix}\right] 减法= \left[\begin{matrix} 0&0\\ 0&0\\ \end{matrix}\right] [0213]+[0213]=[0+02+21+13+3]加法=[0426]减法=[0000]
矩阵的数乘
和矩阵与标量的加减一样,矩阵与标量之间的乘法也是矩阵的每一个元素分别乘以该标量。
[0111]⋅2=[0⋅21⋅21⋅21⋅2]=[0222]\left[\begin{matrix} 0&1\\ 1&1\\ \end{matrix}\right] \cdot 2 = \left[\begin{matrix} 0 \cdot2&1\cdot 2\\ 1\cdot 2&1 \cdot 2\\ \end{matrix}\right]= \left[\begin{matrix} 0&2\\ 2&2\\ \end{matrix}\right] [0111]⋅2=[0⋅21⋅21⋅21⋅2]=[0222]
矩阵相乘
矩阵之间的乘法不见得有多复杂,但的确很难让人适应。矩阵乘法基本上意味着遵照规定好的法则进行相乘。当然,相乘还有一些限制:
- 只有当左侧矩阵的列数与右侧矩阵的行数相等,两个矩阵才能相乘。
- 矩阵相乘不遵守交换律(Commutative),也就是说A⋅B≠B⋅AA \cdot B \not= B \cdot AA⋅B=B⋅A
公式如下:
[1234]⋅[5678]=[1⋅5+2⋅71⋅6+2⋅83⋅5+4⋅73⋅6+4⋅8]=[19224350]\left[\begin{matrix} 1&2\\ 3&4\\ \end{matrix}\right] \cdot \left[\begin{matrix} 5&6\\ 7&8\\ \end{matrix}\right] = \left[\begin{matrix} 1 \cdot 5 + 2 \cdot 7 & 1 \cdot 6+ 2 \cdot 8\\ 3 \cdot 5 + 4 \cdot 7 & 3 \cdot 6+ 4 \cdot 8\\ \end{matrix}\right] = \left[\begin{matrix} 19&22\\ 43&50\\ \end{matrix}\right] [1324]⋅[5768]=[1⋅5+2⋅73⋅5+4⋅71⋅6+2⋅83⋅6+4⋅8]=[19432250]
矩阵与向量相乘
向量就是一个N×1N \times 1N×1的矩阵
单位矩阵就是一个除了对角线以为都是0的 N×NN \times NN×N的矩阵
[1000010000100001]⋅[1234]=[1⋅12⋅23⋅34⋅4]=[1234]\left[\begin{matrix} 1&0&0&0\\ 0&1&0&0\\ 0&0&1&0\\ 0&0&0&1\\ \end{matrix}\right] \cdot \left[\begin{matrix} 1\\ 2\\ 3\\ 4\\ \end{matrix}\right] = \left[\begin{matrix} 1 \cdot 1\\ 2 \cdot 2\\ 3 \cdot 3\\ 4 \cdot 4\\ \end{matrix}\right] = \left[\begin{matrix} 1\\ 2\\ 3\\ 4\\ \end{matrix}\right] 1000010000100001⋅1234=1⋅12⋅23⋅34⋅4=1234
缩放
OpenGL通常是在3D空间进行操作的,对于2D的情况我们可以把z轴缩放1倍,这样z轴的值就不变了。我们刚刚的缩放操作是不均匀(Non-uniform)缩放,因为每个轴的缩放因子(Scaling Factor)都不一样。如果每个轴的缩放因子都一样那么就叫均匀缩放(Uniform Scale)。
[S10000S20000S300001]⋅(xyz1)=(S1⋅xS2⋅yS3⋅z1)\left[\begin{matrix} S1&0&0&0\\ 0&S2&0&0\\ 0&0&S3&0\\ 0&0&0&1\\ \end{matrix}\right] \cdot \left(\begin{matrix} x\\ y\\ z\\ 1\\ \end{matrix}\right) = \left(\begin{matrix} S1 \cdot x\\ S2 \cdot y\\ S3 \cdot z\\ 1\\ \end{matrix}\right) S10000S20000S300001⋅xyz1=S1⋅xS2⋅yS3⋅z1
位移
位移(Translation)是在原始向量的基础上加上另一个向量从而获得一个在不同位置的新向量的过程,从而在位移向量基础上移动了原始向量。我们已经讨论了向量加法,所以这应该不会太陌生。
[100Tx010Ty001Tz0001]⋅(xyz1)=(x+Txy+Tyz+Tz1)\left[\begin{matrix} 1&0&0&Tx\\ 0&1&0&Ty\\ 0&0&1&Tz\\ 0&0&0&1\\ \end{matrix}\right] \cdot \left(\begin{matrix} x\\ y\\ z\\ 1\\ \end{matrix}\right) = \left(\begin{matrix} x + Tx\\ y + Ty\\ z + Tz\\ 1\\ \end{matrix}\right) 100001000010TxTyTz1⋅xyz1=x+Txy+Tyz+Tz1
齐次坐标(Homogeneous Coordinates)
向量的w分量也叫齐次坐标。想要从齐次向量得到3D向量,我们可以把x、y和z坐标分别除以w坐标。我们通常不会注意这个问题,因为w分量通常是1.0。使用齐次坐标有几点好处:它允许我们在3D向量上进行位移(如果没有w分量我们是不能位移向量的),而且下一章我们会用w值创建3D视觉效果。
如果一个向量的齐次坐标是0,这个坐标就是方向向量(Direction Vector),因为w坐标是0,这个向量就不能位移(译注:这也就是我们说的不能位移一个方向)。
旋转
大多数旋转函数需要用弧度制的角:
- 弧度转角度:角度=弧度×(180.0/π)角度 = 弧度 \times (180.0 / \pi)角度=弧度×(180.0/π)
- 角度转弧度:弧度=角度×(π/180.0)弧度 = 角度 \times (\pi / 180.0)弧度=角度×(π/180.0)
沿着x轴旋转:
[10000cosθ−sinθ00sinθcosθ00001]⋅(xyz1)=(xcosθ⋅y−sinθ⋅zsinθ⋅y+cosθ⋅z1)\left[\begin{matrix} 1&0&0&0\\ 0&cos\theta&-sin\theta&0\\ 0&sin\theta&cos\theta&0\\ 0&0&0&1\\ \end{matrix}\right] \cdot \left(\begin{matrix} x\\ y\\ z\\ 1\\ \end{matrix}\right) = \left(\begin{matrix} x\\ cos\theta\cdot y - sin\theta\cdot z\\ sin\theta\cdot y + cos\theta\cdot z\\ 1\\ \end{matrix}\right) 10000cosθsinθ00−sinθcosθ00001⋅xyz1=xcosθ⋅y−sinθ⋅zsinθ⋅y+cosθ⋅z1
沿着y轴旋转:
[cosθ0sinθ00100−sinθ0cosθ00001]⋅(xyz1)=(cosθ⋅x+sinθ⋅zy−sinθ⋅x+cosθ⋅z1)\left[\begin{matrix} cos\theta&0&sin\theta&0\\ 0&1&0&0\\ -sin\theta&0&cos\theta&0\\ 0&0&0&1\\ \end{matrix}\right] \cdot \left(\begin{matrix} x\\ y\\ z\\ 1\\ \end{matrix}\right) = \left(\begin{matrix} cos\theta\cdot x+ sin\theta\cdot z\\ y \\ -sin\theta\cdot x + cos\theta\cdot z\\ 1\\ \end{matrix}\right) cosθ0−sinθ00100sinθ0cosθ00001⋅xyz1=cosθ⋅x+sinθ⋅zy−sinθ⋅x+cosθ⋅z1
沿着z轴旋转:
[cosθ−sinθ00sinθcosθ0000100001]⋅(xyz1)=(cosθ⋅x−sinθ⋅ysinθ⋅x+cosθ⋅yz1)\left[\begin{matrix} cos\theta&-sin\theta&0&0\\ sin\theta&cos\theta&0&0\\ 0&0&1&0\\ 0&0&0&1\\ \end{matrix}\right] \cdot \left(\begin{matrix} x\\ y\\ z\\ 1\\ \end{matrix}\right) = \left(\begin{matrix} cos\theta\cdot x - sin\theta\cdot y\\ sin\theta\cdot x + cos\theta\cdot y \\ z \\ 1\\ \end{matrix}\right) cosθsinθ00−sinθcosθ0000100001⋅xyz1=cosθ⋅x−sinθ⋅ysinθ⋅x+cosθ⋅yz1
矩阵的组合
使用矩阵进行变换的真正力量在于,根据矩阵之间的乘法,我们可以把多个变换组合到一个矩阵中。让我们看看我们是否能生成一个变换矩阵,让它组合多个变换。假设我们有一个顶点(x, y, z),我们希望将其缩放2倍,然后位移(1, 2, 3)个单位。我们需要一个位移和缩放矩阵来完成这些变换。结果的变换矩阵看起来像这样:
[1001010200130001]⋅[2000020000200001]=[2001020200230001]\left[\begin{matrix} 1&0&0&1\\ 0&1&0&2\\ 0&0&1&3\\ 0&0&0&1\\ \end{matrix}\right] \cdot \left[\begin{matrix} 2&0&0&0\\ 0&2&0&0\\ 0&0&2&0\\ 0&0&0&1\\ \end{matrix}\right] = \left[\begin{matrix} 2&0&0&1\\ 0&2&0&2\\ 0&0&2&3\\ 0&0&0&1\\ \end{matrix}\right] 1000010000101231⋅2000020000200001=2000020000201231
用最终的变换矩阵左乘我们的向量会得到以下结果:
[2001020200230001]⋅(xyz1)=(2x+12y+22z+31)\left[\begin{matrix} 2&0&0&1\\ 0&2&0&2\\ 0&0&2&3\\ 0&0&0&1\\ \end{matrix}\right] \cdot \left(\begin{matrix} x\\ y\\ z\\ 1\\ \end{matrix}\right) = \left(\begin{matrix} 2x + 1\\ 2y + 2\\ 2z + 3 \\ 1\\ \end{matrix}\right) 2000020000201231⋅xyz1=2x+12y+22z+31
代码实现
#version 330 core
layout (location = 0) in vec3 aPos;
layout (location = 1) in vec3 aColor;
layout (location = 1) in vec2 aTexCord;
out vec3 ourColor; // 向片段着色器输出一个颜色
out vec2 texCord; // 向片段着色器输出一个颜色
uniform mat4 RotationMatrix;
void main()
{gl_Position = RotationMatrix * vec4(aPos, 1.0);ourColor = aColor; // 将ourColor设置为我们从顶点数据那里得到的输入颜色texCord = aTexCord;
}
QMatrix4x4 matrix;
unsigned int time = QTime::currentTime().msec();
matrix.translate(3,3);
matrix.rotate(time, 0.0f, 0.0f, 1.0f);
...
shader_program_.setUniformValue("RotationMatrix", matrix);
相关文章:

QT+ OpenGL 变换
文章目录QT OpenGL变换向量的运算矩阵矩阵与向量相乘代码实现QT OpenGL 本篇完整工程见gitee:QTOpenGL 对应点的tag,由turbolove提供技术支持,您可以关注博主或者私信博主。 变换 我们需要改变物体的位置 现有解决办法(每一帧,…...
【算法】前缀和
作者:指针不指南吗 专栏:算法篇 🐾要学会在纸上打草稿,这个很重要🐾 文章目录1.什么是前缀和?2.怎么求前缀和?3.前缀和有什么用?4.进阶二维:矩阵和前缀和 主打一个记公式 1.什么是前…...
《Redis实战篇》七、Redis消息队列
7.1 Redis消息队列-认识消息队列 什么是消息队列:字面意思就是存放消息的队列。最简单的消息队列模型包括3个角色: 消息队列:存储和管理消息,也被称为消息代理(Message Broker)生产者:发送消息…...

android组件化
学习流程:1.开源最佳实践:Android平台页面路由框架ARouter-阿里云开发者社区 (aliyun.com)2.中文ARouter使用API:https://github.com/alibaba/ARouter/blob/master/README_CN.md3.看当前文档后面的代码4.这是通俗易懂的文章:https…...
)
华为OD机试真题Python实现【特异性双端队列】真题+解题思路+代码(20222023)
🔥系列专栏 华为OD机试(Python)真题目录汇总华为OD机试(JAVA)真题目录汇总华为OD机试(C++)真题目录汇总华为OD机试(JavaScript)真题目录汇总文章目录 🔥系列专栏题目输入输出示例一输入输出解题思路核心知识点Python 代码实现代码运行结果版权说明<...

24.架构能力
文章目录24. 架构能力24.1 Competence of Individuals: Duties, Skills, and Knowledge of Architects 个人能力:架构师的职责、技能和知识24.2 Competence of a Software Architecture Organization 软件架构组织的能力24.3 Summary 小结24.4 For Further Reading …...

前端原生 CSS 跑马灯效果,无限轮播(横竖版本,带渐变遮罩,简单实用)
一、横版跑马灯 <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><meta http-equiv"X-UA-Compatible" content"IEedge"><meta name"viewport" content"widthdevice-wid…...
4.8 注解与自定义注解
文章目录1.概述2.注解的分类2.1 JDK注解2.2 元注解2.2.1 Target ElementType…2.2.2 Retention RetentionPolicy…3 自定义注解1.概述 在注解刚出现时,曾受到过好多程序员的鄙夷,觉得这就是多此一举的操作; 但随着时间的推移,越…...

webpack 的热更新是如何做到的?原理是什么?
Hot Module Replacement,简称 HMR,在不需要刷新整个页面的同时更新模块,能够提升开发的效率和体验。热更新时只会局部刷新页面上发生了变化的模块,同时可以保留当前页面的状态,比如复选框的选中状态等。 在 webpack 中…...
嵌入式ARM设计编程(一) 简单数据搬移
文章和代码已归档至【Github仓库:hardware-tutorial】,需要的朋友们自取。或者公众号【AIShareLab】回复 嵌入式 也可获取。 一、实验目的 熟悉实验开发环境,掌握简单ARM汇编指令的使用方法。 二、实验环境 硬件:PC机 软件&am…...

【Selenium】十分钟手把手带你学会WebDriver API
目录 1、定位元素【8种】 2、操作测试对象 3、添加等待 4、弹窗类型 5、浏览器的操作 6、键盘事件 7、选择框 8、上传文件 1、定位元素【8种】 元素定位是自动化测试的核心,想要去操作一个对象,第一步就是需要我们先去识别这个对象。每个对象就会…...
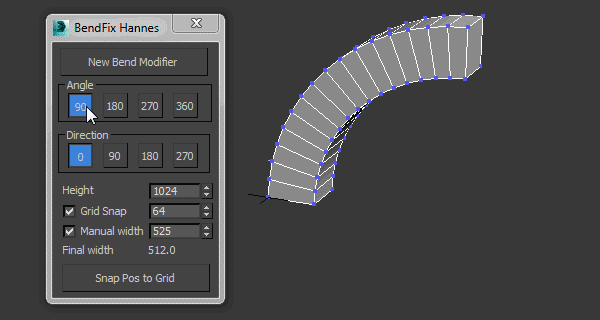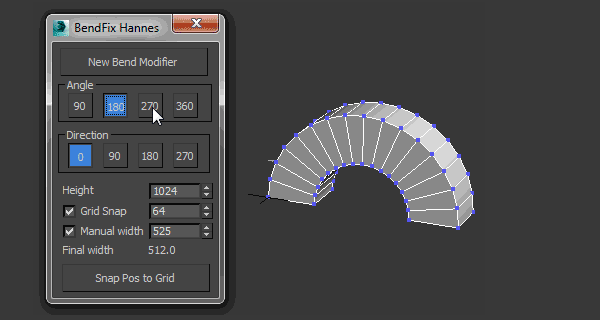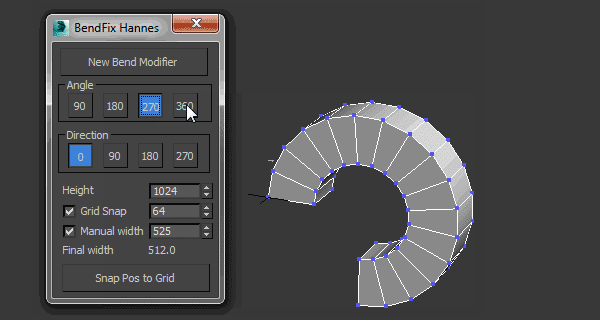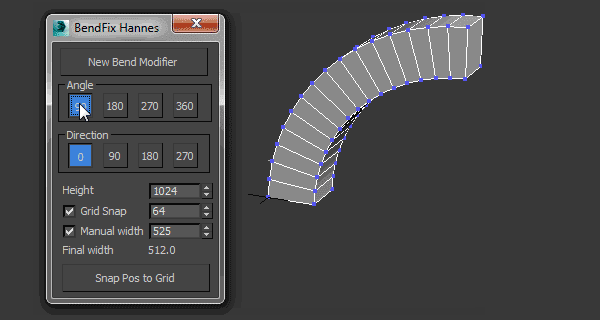
3DMAX高级弯曲插件使用教程
3dMax高级弯曲插件是对3dmax原生“弯曲(Bend)”修改器的一个增强,给用户更多控制弯曲修改器的参数设置,它让用户输入宽度,插件脚本将移动中心以获得正确的宽度。 主要特性: - 使用智能捕捉捕捉到自定义网格…...

前端面试题之性能优化大杂烩
主要内容为下面几大类:移动端、图片、JavaScript、css、html、页面内容、服务器、cookie。 移动端性能优化: 保持单个文件小于25KB 移动网站页面要求下载资源,如果文件过大,会大大减慢页面加载速度。 打包内容为分段multipart文…...
SpringBoot+Vue实现养老智慧服务平台
文末获取源码 开发语言:Java 框架:springboot JDK版本:JDK1.8 服务器:tomcat7 数据库:mysql 5.7/8.0 数据库工具:Navicat11 开发软件:eclipse/myeclipse/idea Maven包:Maven3.3.9 浏…...

tigervnc2023
sudo apt-get install tigervnc-standalone-server 配置用户 /etc/tigervnc/vncserver.users :1user1 :2user2 :3user3 全局配置 /etc/tigervnc/vncserver-config-defaults $localhost"no"; $geometry "1920x1200"; 分别进入user1 user2 user3 用户…...

智能三子棋(人机大战)—— 你会是最终赢家吗?万字讲解让你实现与自己对弈
魔王的介绍:😶🌫️一名双非本科大一小白。魔王的目标:🤯努力赶上周围卷王的脚步。魔王的主页:🔥🔥🔥大魔王.🔥🔥🔥 ❤️…...
【自制开发板】自制STM32F407开发板(含TFT 8080串口屏幕接口)
【2023 年 2 月 14 日】 许久没有更新,最近做了个小开发板玩了玩。更新一下吧,作为记录!! 主要是象试一下LVGL在STM32上的应用,所以开发板的大小都是基于屏幕大小来设计的。 分享出来,给大家一个板子结构…...

openvino yolov5/ssd 实时推流目标检测在html上显示
安装ffmepg并添加到环境变量中,流媒体使用m7s 运行效果 SSD:检测在10ms左右,yolov5在100ms左右 app.py #!/usr/local/bin/python3 # encodin: utf-8import subprocess import threading import time import cv2 import osfrom OpenVinoYoloV…...
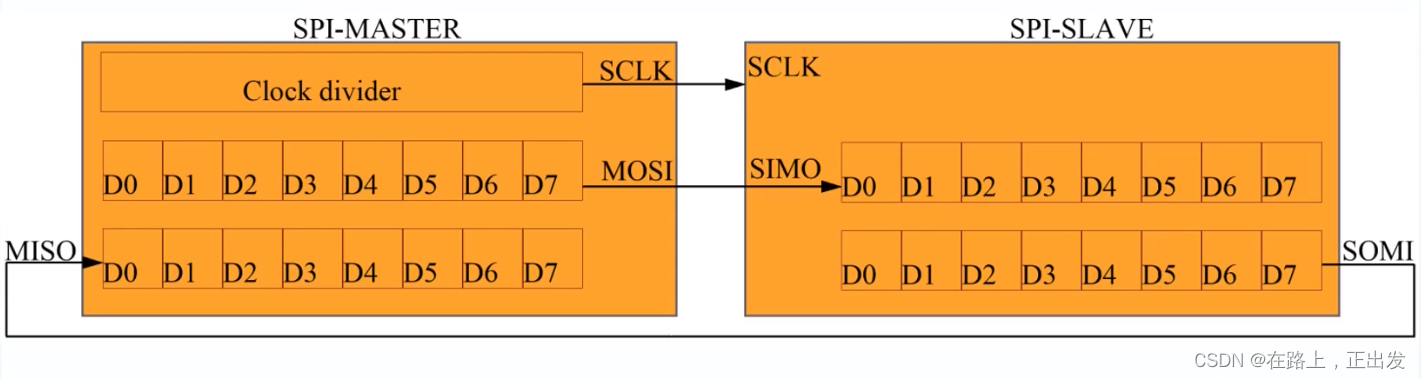
基于FPGA的 SPI通信 设计(1)
引言 低速通信目前搞过 UART串口通信、IIC通信。其实 SPI 也算是中低速(有时也可以用作高速通信)串行通信的范畴,但是一直还没真正实现过,所以此系列就 SPI的协议以及FPGA设计作几篇博客记录。欢迎订阅关注~ SPI 标准协议 x1模式…...
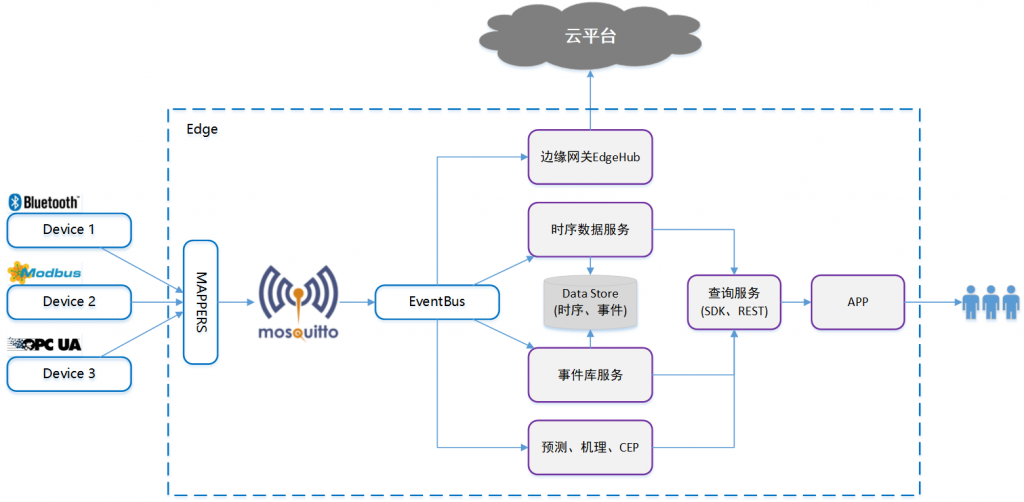
为什么西门子、美的等企业这样进行架构升级,看看改造效果就知道了
在工业领域, 生产、测试、运行阶段都可能会产生大量带有时间戳的传感器数据,这都属于典型的时序数据。时序数据主要由各类型实时监测、检查与分析设备所采集或产生,涉及制造、电力、化工、工程作业等多个行业,具备写多读少、量非常…...

【OSG学习笔记】Day 18: 碰撞检测与物理交互
物理引擎(Physics Engine) 物理引擎 是一种通过计算机模拟物理规律(如力学、碰撞、重力、流体动力学等)的软件工具或库。 它的核心目标是在虚拟环境中逼真地模拟物体的运动和交互,广泛应用于 游戏开发、动画制作、虚…...

DeepSeek 赋能智慧能源:微电网优化调度的智能革新路径
目录 一、智慧能源微电网优化调度概述1.1 智慧能源微电网概念1.2 优化调度的重要性1.3 目前面临的挑战 二、DeepSeek 技术探秘2.1 DeepSeek 技术原理2.2 DeepSeek 独特优势2.3 DeepSeek 在 AI 领域地位 三、DeepSeek 在微电网优化调度中的应用剖析3.1 数据处理与分析3.2 预测与…...

从深圳崛起的“机器之眼”:赴港乐动机器人的万亿赛道赶考路
进入2025年以来,尽管围绕人形机器人、具身智能等机器人赛道的质疑声不断,但全球市场热度依然高涨,入局者持续增加。 以国内市场为例,天眼查专业版数据显示,截至5月底,我国现存在业、存续状态的机器人相关企…...

C# 类和继承(抽象类)
抽象类 抽象类是指设计为被继承的类。抽象类只能被用作其他类的基类。 不能创建抽象类的实例。抽象类使用abstract修饰符声明。 抽象类可以包含抽象成员或普通的非抽象成员。抽象类的成员可以是抽象成员和普通带 实现的成员的任意组合。抽象类自己可以派生自另一个抽象类。例…...

数据库分批入库
今天在工作中,遇到一个问题,就是分批查询的时候,由于批次过大导致出现了一些问题,一下是问题描述和解决方案: 示例: // 假设已有数据列表 dataList 和 PreparedStatement pstmt int batchSize 1000; // …...

站群服务器的应用场景都有哪些?
站群服务器主要是为了多个网站的托管和管理所设计的,可以通过集中管理和高效资源的分配,来支持多个独立的网站同时运行,让每一个网站都可以分配到独立的IP地址,避免出现IP关联的风险,用户还可以通过控制面板进行管理功…...

通过 Ansible 在 Windows 2022 上安装 IIS Web 服务器
拓扑结构 这是一个用于通过 Ansible 部署 IIS Web 服务器的实验室拓扑。 前提条件: 在被管理的节点上安装WinRm 准备一张自签名的证书 开放防火墙入站tcp 5985 5986端口 准备自签名证书 PS C:\Users\azureuser> $cert New-SelfSignedCertificate -DnsName &…...

学习一下用鸿蒙DevEco Studio HarmonyOS5实现百度地图
在鸿蒙(HarmonyOS5)中集成百度地图,可以通过以下步骤和技术方案实现。结合鸿蒙的分布式能力和百度地图的API,可以构建跨设备的定位、导航和地图展示功能。 1. 鸿蒙环境准备 开发工具:下载安装 De…...

Ubuntu系统复制(U盘-电脑硬盘)
所需环境 电脑自带硬盘:1块 (1T) U盘1:Ubuntu系统引导盘(用于“U盘2”复制到“电脑自带硬盘”) U盘2:Ubuntu系统盘(1T,用于被复制) !!!建议“电脑…...

区块链技术概述
区块链技术是一种去中心化、分布式账本技术,通过密码学、共识机制和智能合约等核心组件,实现数据不可篡改、透明可追溯的系统。 一、核心技术 1. 去中心化 特点:数据存储在网络中的多个节点(计算机),而非…...
