嵌入式ARM设计编程(一) 简单数据搬移
文章和代码已归档至【Github仓库:hardware-tutorial】,需要的朋友们自取。或者公众号【AIShareLab】回复 嵌入式 也可获取。
一、实验目的
熟悉实验开发环境,掌握简单ARM汇编指令的使用方法。
二、实验环境
硬件:PC机
软件:ADS1.2 集成开发环境
三、实验内容
熟悉开发环境并使用LDR/STR,MOV等指令访问寄存器或存储单元;
使用ADD/SUB/LSL/LSR/AND/ORR等指令,完成基本数学/逻辑运算。
四、实验要求
(1)按照2.3节介绍的方法, 在ADS下创建一个工程asmlab1,定义两个变量x,y和堆栈地址0x1000,将变量x的内容存到堆栈顶,然后计算x+y,并将和存到堆栈的下一个单元。通过AXD查看寄存器和memory和寄存器中数据变化。
(2)在指令后面加上适当注释,说明指令功能。
(3)指出程序执行完成后各相关寄存器及存储器单元的具体内容。
五、实验完成情况
1、实验源代码(含注释):
AREA Init,CODE,READONLY ;伪指令AREA定义名为Init,属性为只读或的代码片段ENTRY ;伪指令ENTRY声明程序入口CODE32 ;声明以下代码为 32 位 ARM 指令
x EQU 45
y EQU 64 ;定义两个变量 x,y
stack_top EQU 0x1000 ;定义堆栈地址 0x1000
start MOV SP, #stack_top ;设置栈顶地址MOV R0, #x ;把x的值赋给R0STR R0, [SP] ;R0中的内容入栈
MOV R0, #y ;把y的值赋给R0
LDR R1, [SP] ; 数据出栈,放入R1,即R1中放x的值ADD R0, R0, R1 ;R0=R0+R1STR R0, [SP,#4] ;先执行SP+4(ARM为32位指令集),再将R0内容复制到SP指向的寄存器B .
END ;程序结束
2、实验过程(含结果截图及相应文字解释):
根据代码可知,
1.首先执行start MOV SP, #stack_top 通过该语句设置了栈顶地址为0x1000。
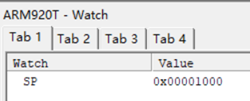
2.然后执行MOV R0, #x,把x的值赋值给了R0寄存器,此时R0寄存器的值变成45,由于是十六进制存储的,因此显示为2D。
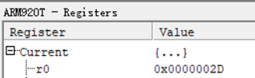
3.然后执行STR R0, [SP],将R0的值入栈,由于前面已经设置了栈顶地址为0x1000,因此可以查看到内存地址0x100处的数据变成了2D。
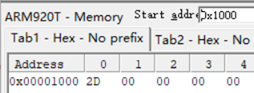
4.然后执行MOV R0, #y,把y的值赋值给了R0寄存器,此时R0寄存器的值变成64,由于是十六进制存储的,因此显示为40。
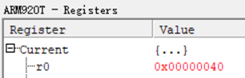
5.然后执行LDR R1, [SP],该数据出栈,将数据赋值给R1,此时R1中保存的值为2D。
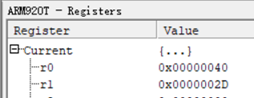
6.然后执行ADD R0, R0, R1,其含义相当于R0=R0+R1,因此R0寄存器的值为2D+40 = 6D。
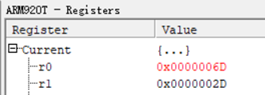
7.最后执行STR R0, [SP, #4],先执行SP+4,将指针进行偏移,再将R0的值复制到此时SP指向的地址0x1004,该数据赋值为6D。
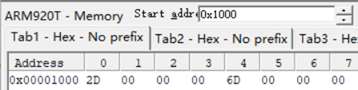
最后程序执行完成后各相关寄存器及存储器单元的具体内容如下:
寄存器:
- R0内容为0x6D,
- R1内容为0x2D,
- SP内容为0x1000,
存储器单元:
- 0x1000内容为0x2D,
- 0x1004内容为0x6D。
练习题
编写程序实现对一段数据的最大值最小值搜索,最大值存于max变量之中,最小值存于min变量之中。
提示: 数据的定义采用伪指令:DCD来实现,如:
DataBuf DCD 11,-2,35,47,96,63,128,-23
搜索最大值和最小值可以利用两个寄存器R1,R2来存放。用到的比较指令为CMP,用到的条件标识符小于为LT,大于为GT。
基本思路为:利用R0做基地址,将R1,R2分别存入第一个单元的内容,利用R3做循环计数器,利用R4遍历读取第2至最后一个数据,如果R1的数据小于新读入的R4数据则将R4的内容存入R1, 如果R2的内容大于R4的内容则将R4的内容存入R2。遍历完成之后,R1将存放最大数据,R2将存放最小数据。
AREA comp,CODE,READONLY ;定义CODE片段comp 只读ENTRY ;进入程序CODE32 ;以下为32位的ARM程序
START LDR R0, = DAT ;加载数据段中DAT的数据的地址到R0LDR R1, [R0] ;加载R0的内容到R1LDR R2, [R0] ;加载R0的内容到R1MOV R3,#1 ;设置循环变量R3并初始化为1
LOOPADD R0,R0,#4 ;每次循环R0+4LDR R4,[R0] ;R4存入R0的数据CMP R1,R4 ;比较R1,R4MOVLT R1,R4 ;如果R1<R4 就把R4存入R1CMP R2,R4 ;比较R2,R4MOVGT R2,R4 ;如果R2>R4 就把R4存入R2ADD R3,R3,#1 ;每次循环R3值加一CMP R3,#8 ;判断R3与8BLT LOOP ;如果R3 < 8则跳转到LOOP执行B . ;退出AREA D,DATA,READONLY ;定义一个数据段D,读写
DAT DCD 11,-2,35,47,96,63,128,-23END
实验结果如下:
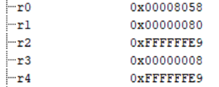
程序的基本思路是将DataBuf的首地址装载到R0中,再通过首地址将第一个数据装载到R1和R2中,设定R3为循环变量,并且初始化为1。然后进入循环,通过循环比较,将比较过程中得到的最大值放在R1中,最小值放在R2中,每一次循环R3中的值加1,当R3=8时,比较循环结束。
相关文章:

嵌入式ARM设计编程(一) 简单数据搬移
文章和代码已归档至【Github仓库:hardware-tutorial】,需要的朋友们自取。或者公众号【AIShareLab】回复 嵌入式 也可获取。 一、实验目的 熟悉实验开发环境,掌握简单ARM汇编指令的使用方法。 二、实验环境 硬件:PC机 软件&am…...

【Selenium】十分钟手把手带你学会WebDriver API
目录 1、定位元素【8种】 2、操作测试对象 3、添加等待 4、弹窗类型 5、浏览器的操作 6、键盘事件 7、选择框 8、上传文件 1、定位元素【8种】 元素定位是自动化测试的核心,想要去操作一个对象,第一步就是需要我们先去识别这个对象。每个对象就会…...
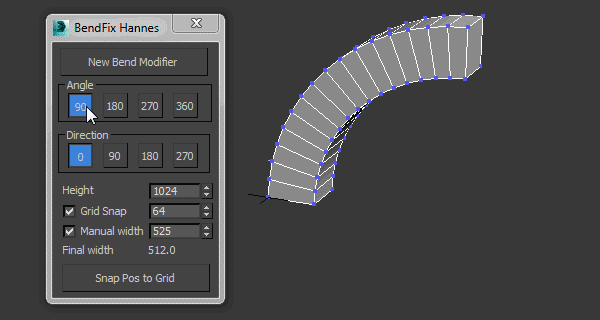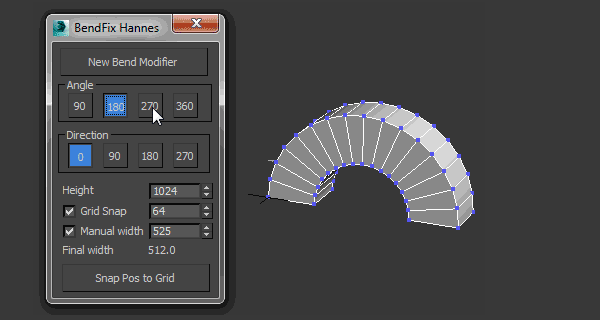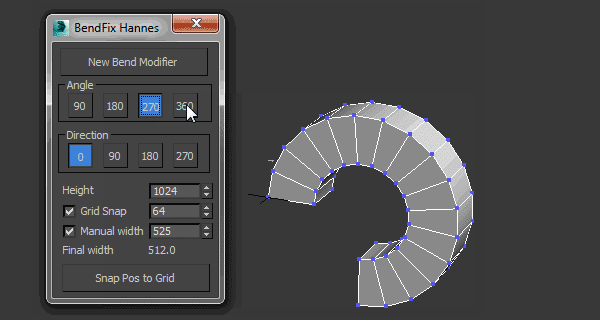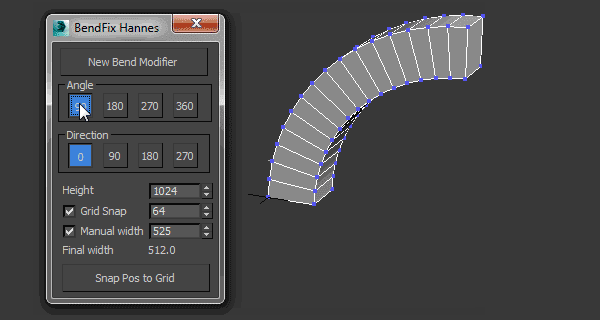
3DMAX高级弯曲插件使用教程
3dMax高级弯曲插件是对3dmax原生“弯曲(Bend)”修改器的一个增强,给用户更多控制弯曲修改器的参数设置,它让用户输入宽度,插件脚本将移动中心以获得正确的宽度。 主要特性: - 使用智能捕捉捕捉到自定义网格…...

前端面试题之性能优化大杂烩
主要内容为下面几大类:移动端、图片、JavaScript、css、html、页面内容、服务器、cookie。 移动端性能优化: 保持单个文件小于25KB 移动网站页面要求下载资源,如果文件过大,会大大减慢页面加载速度。 打包内容为分段multipart文…...
SpringBoot+Vue实现养老智慧服务平台
文末获取源码 开发语言:Java 框架:springboot JDK版本:JDK1.8 服务器:tomcat7 数据库:mysql 5.7/8.0 数据库工具:Navicat11 开发软件:eclipse/myeclipse/idea Maven包:Maven3.3.9 浏…...

tigervnc2023
sudo apt-get install tigervnc-standalone-server 配置用户 /etc/tigervnc/vncserver.users :1user1 :2user2 :3user3 全局配置 /etc/tigervnc/vncserver-config-defaults $localhost"no"; $geometry "1920x1200"; 分别进入user1 user2 user3 用户…...

智能三子棋(人机大战)—— 你会是最终赢家吗?万字讲解让你实现与自己对弈
魔王的介绍:😶🌫️一名双非本科大一小白。魔王的目标:🤯努力赶上周围卷王的脚步。魔王的主页:🔥🔥🔥大魔王.🔥🔥🔥 ❤️…...
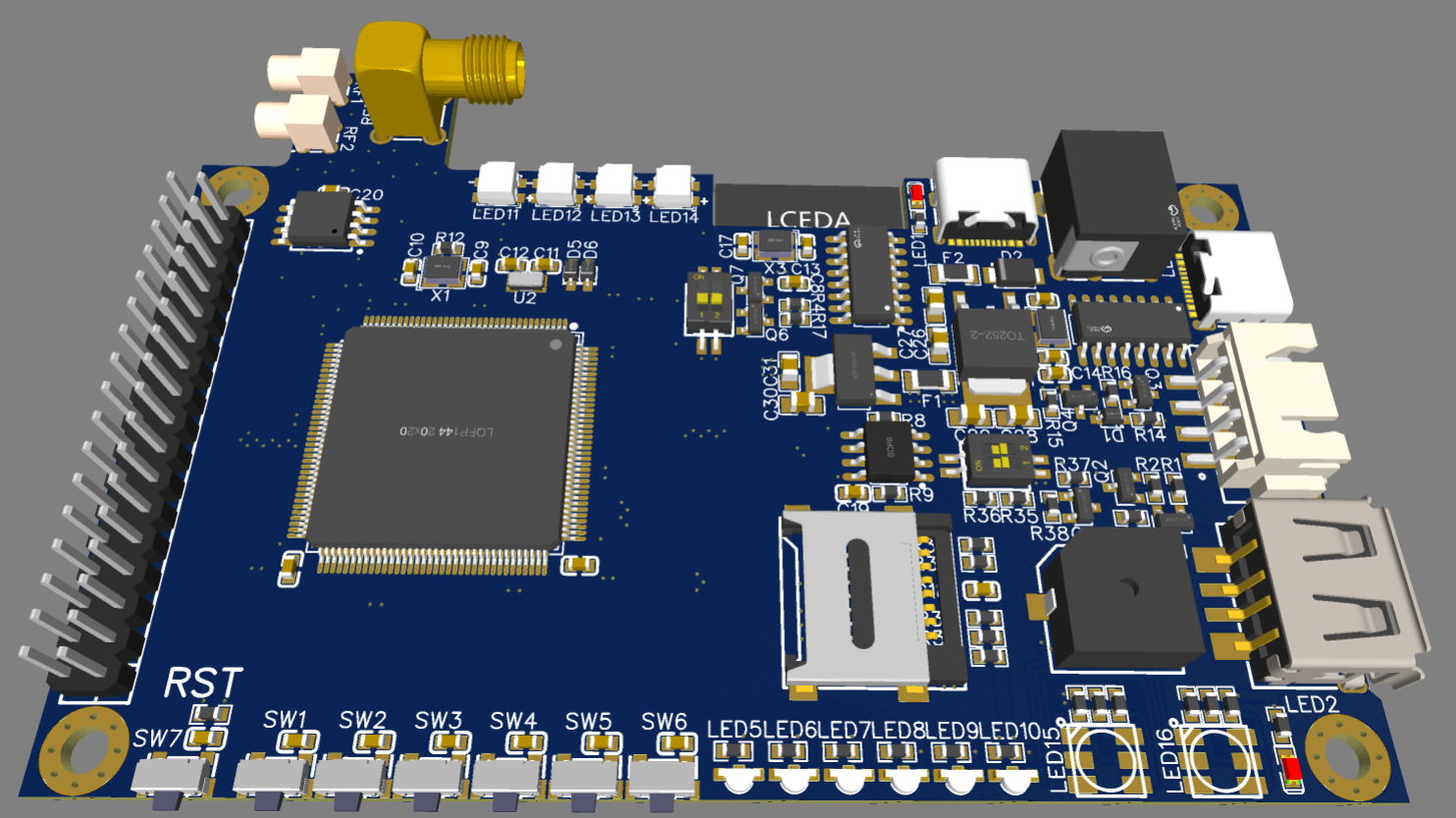
【自制开发板】自制STM32F407开发板(含TFT 8080串口屏幕接口)
【2023 年 2 月 14 日】 许久没有更新,最近做了个小开发板玩了玩。更新一下吧,作为记录!! 主要是象试一下LVGL在STM32上的应用,所以开发板的大小都是基于屏幕大小来设计的。 分享出来,给大家一个板子结构…...

openvino yolov5/ssd 实时推流目标检测在html上显示
安装ffmepg并添加到环境变量中,流媒体使用m7s 运行效果 SSD:检测在10ms左右,yolov5在100ms左右 app.py #!/usr/local/bin/python3 # encodin: utf-8import subprocess import threading import time import cv2 import osfrom OpenVinoYoloV…...
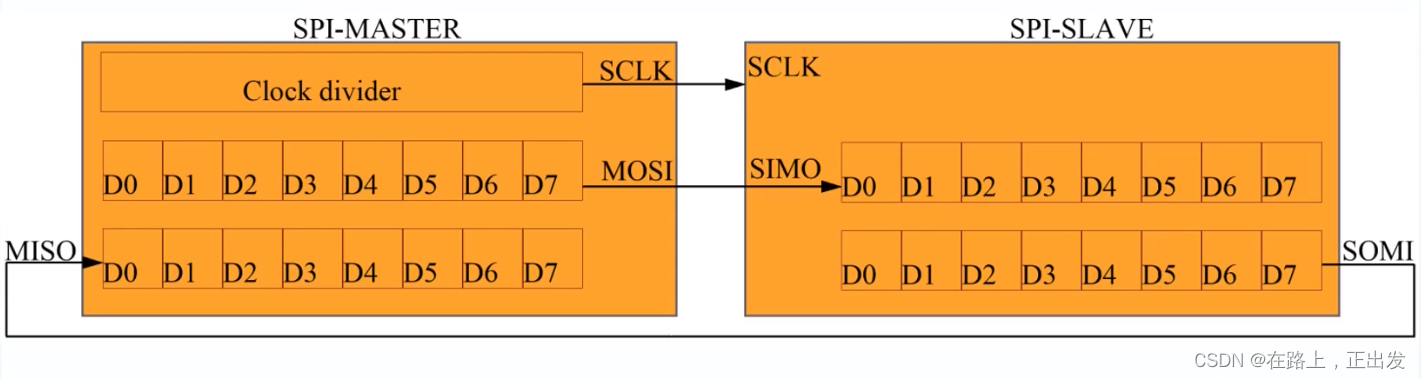
基于FPGA的 SPI通信 设计(1)
引言 低速通信目前搞过 UART串口通信、IIC通信。其实 SPI 也算是中低速(有时也可以用作高速通信)串行通信的范畴,但是一直还没真正实现过,所以此系列就 SPI的协议以及FPGA设计作几篇博客记录。欢迎订阅关注~ SPI 标准协议 x1模式…...
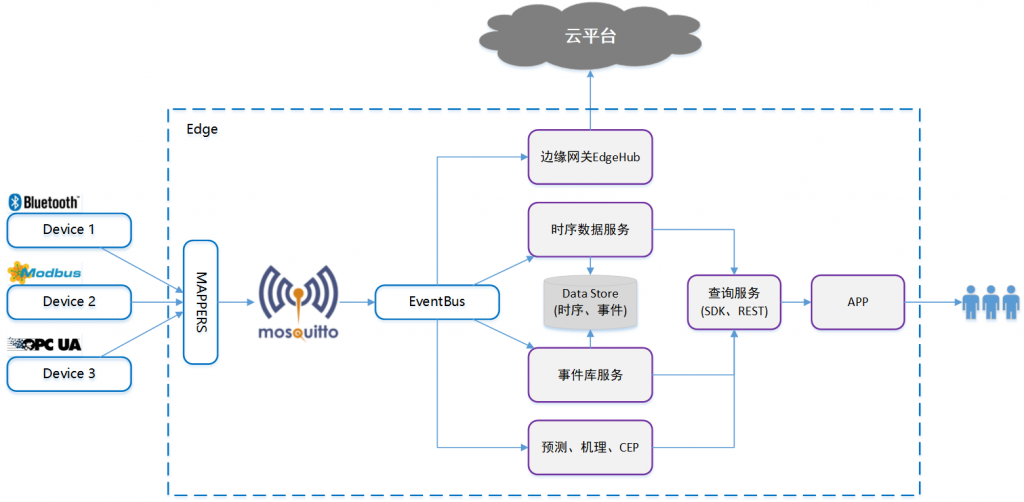
为什么西门子、美的等企业这样进行架构升级,看看改造效果就知道了
在工业领域, 生产、测试、运行阶段都可能会产生大量带有时间戳的传感器数据,这都属于典型的时序数据。时序数据主要由各类型实时监测、检查与分析设备所采集或产生,涉及制造、电力、化工、工程作业等多个行业,具备写多读少、量非常…...

open3d点云配准函数registration_icp
文章目录基本原理open3d调用绘图基本原理 ICP, 即Iterative Closest Point, 迭代点算法。 ICP算法有多种形式,其中最简单的思路就是比较点与点之间的距离,对于点云P{pi},Q{qi}P\{p_i\}, Q\{q_i\}P{pi},Q{qi}而言,如果二者是同一目标&am…...
HTML编码规范
本篇文章是基于王叨叨大佬师父维护的文档梳理的,有兴趣可以去看一下原文HTML编码规范。 1. 缩进与换行 【建议】 使用 2 个空格作为一个缩进层级,不允许使用tab字符 解释: 具体项目,可以使用2个空格,也可以使用…...

PDF SDK for Linux 8.4.2 Crack
PDF SDK for Linux 是适用于任何 Linux 企业或云应用程序的强大解决方案,非常适合需要完全可定制的 PDF 查看器或后端流程的任何 Linux 开发人员。 将 Foxit PDF SDK 嵌入到基于 Linux 的应用程序中非常容易。只需打开您最喜欢的 Linux IDE,复制您需要的…...

vb 模块和作用域的关系
模块在VB中有三种类型的模块,分别是窗体模块、标准模块和类模块。窗体模块窗体模块中包含了窗体以及窗体中所有控件的事件过程,文件扩展名为(*.frm),窗体文件中不仅包含窗体对象的外观设计,也包含窗体模块(…...
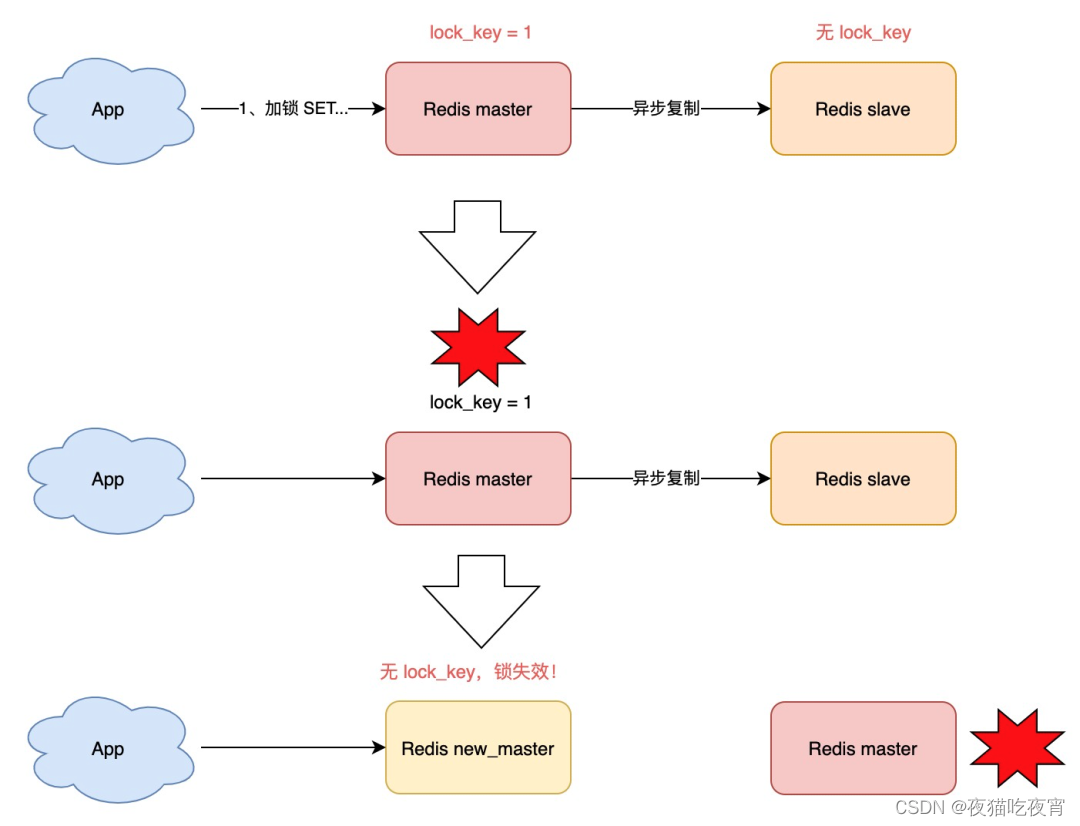
Redis分布式锁
一、背景 与分布式锁相对应的是「单机锁」,我们在写多线程程序时,避免同时操作一个共享变量产生数据问题,通常会使用一把锁来「互斥」,以保证共享变量的正确性,其使用范围是在「同一个进程」中。单机环境下࿰…...

京东前端经典面试题整理
img的srcset属性的作⽤? 响应式页面中经常用到根据屏幕密度设置不同的图片。这时就用到了 img 标签的srcset属性。srcset属性用于设置不同屏幕密度下,img 会自动加载不同的图片。用法如下: <img src"image-128.png" srcset&qu…...

django+mysql实现一个简单的web登录页面
目录 一、使用pyacharm创建一个django项目 二、启动django项目验证 三、配置mysql数据库 1、本地安装mysql数据库 1)安装mysql数据库 2)自己创建一个数据库 2、安装 pymysql 3、配置mysql数据库 1)在项目同名包下的_init_.py里面添加…...

python cartopy手动导入地图数据绘制底图/python地图上绘制散点图:Downloading:warnings/散点图添加图里标签
……开学回所,打开电脑spyder一看一脸懵逼,简直不敢相信这些都是我自己用过的代码,想把以前的自己喊过来科研了() 废话少说,最近写小综述论文,需要绘制一个地图底图+散点图ÿ…...

JavaScript中常用的数组方法
在日常开发中,我们会接触到js中数组的一些方法,这些方法对我们来说,可以很便利的达到我们想要的结果,但是因为方法比较多,有些方法也不常用,可能会过一段时间就会忘记,那么在这里我整理了一些数…...

铭豹扩展坞 USB转网口 突然无法识别解决方法
当 USB 转网口扩展坞在一台笔记本上无法识别,但在其他电脑上正常工作时,问题通常出在笔记本自身或其与扩展坞的兼容性上。以下是系统化的定位思路和排查步骤,帮助你快速找到故障原因: 背景: 一个M-pard(铭豹)扩展坞的网卡突然无法识别了,扩展出来的三个USB接口正常。…...
)
Spring Boot 实现流式响应(兼容 2.7.x)
在实际开发中,我们可能会遇到一些流式数据处理的场景,比如接收来自上游接口的 Server-Sent Events(SSE) 或 流式 JSON 内容,并将其原样中转给前端页面或客户端。这种情况下,传统的 RestTemplate 缓存机制会…...
)
IGP(Interior Gateway Protocol,内部网关协议)
IGP(Interior Gateway Protocol,内部网关协议) 是一种用于在一个自治系统(AS)内部传递路由信息的路由协议,主要用于在一个组织或机构的内部网络中决定数据包的最佳路径。与用于自治系统之间通信的 EGP&…...

微信小程序 - 手机震动
一、界面 <button type"primary" bindtap"shortVibrate">短震动</button> <button type"primary" bindtap"longVibrate">长震动</button> 二、js逻辑代码 注:文档 https://developers.weixin.qq…...

CMake 从 GitHub 下载第三方库并使用
有时我们希望直接使用 GitHub 上的开源库,而不想手动下载、编译和安装。 可以利用 CMake 提供的 FetchContent 模块来实现自动下载、构建和链接第三方库。 FetchContent 命令官方文档✅ 示例代码 我们将以 fmt 这个流行的格式化库为例,演示如何: 使用 FetchContent 从 GitH…...

图表类系列各种样式PPT模版分享
图标图表系列PPT模版,柱状图PPT模版,线状图PPT模版,折线图PPT模版,饼状图PPT模版,雷达图PPT模版,树状图PPT模版 图表类系列各种样式PPT模版分享:图表系列PPT模板https://pan.quark.cn/s/20d40aa…...

【Go语言基础【12】】指针:声明、取地址、解引用
文章目录 零、概述:指针 vs. 引用(类比其他语言)一、指针基础概念二、指针声明与初始化三、指针操作符1. &:取地址(拿到内存地址)2. *:解引用(拿到值) 四、空指针&am…...
)
C++课设:简易日历程序(支持传统节假日 + 二十四节气 + 个人纪念日管理)
名人说:路漫漫其修远兮,吾将上下而求索。—— 屈原《离骚》 创作者:Code_流苏(CSDN)(一个喜欢古诗词和编程的Coder😊) 专栏介绍:《编程项目实战》 目录 一、为什么要开发一个日历程序?1. 深入理解时间算法2. 练习面向对象设计3. 学习数据结构应用二、核心算法深度解析…...

计算机基础知识解析:从应用到架构的全面拆解
目录 前言 1、 计算机的应用领域:无处不在的数字助手 2、 计算机的进化史:从算盘到量子计算 3、计算机的分类:不止 “台式机和笔记本” 4、计算机的组件:硬件与软件的协同 4.1 硬件:五大核心部件 4.2 软件&#…...

Qt 事件处理中 return 的深入解析
Qt 事件处理中 return 的深入解析 在 Qt 事件处理中,return 语句的使用是另一个关键概念,它与 event->accept()/event->ignore() 密切相关但作用不同。让我们详细分析一下它们之间的关系和工作原理。 核心区别:不同层级的事件处理 方…...
