传奇私服搭建网站的几种方法
搭建网站的几种方法：
一些人，连简单的搭建网站都不会，还要请技术帮忙，真是牛B，这里简单介绍下几种办法
一：2003系统下，直接使用IIS，这个太简单了，桌面上就有IIS，打开IIS之后，看下面2008系统的，基本一样！
二：2008系统，一些人说，找不到IIS，我们需要先安装下IIS
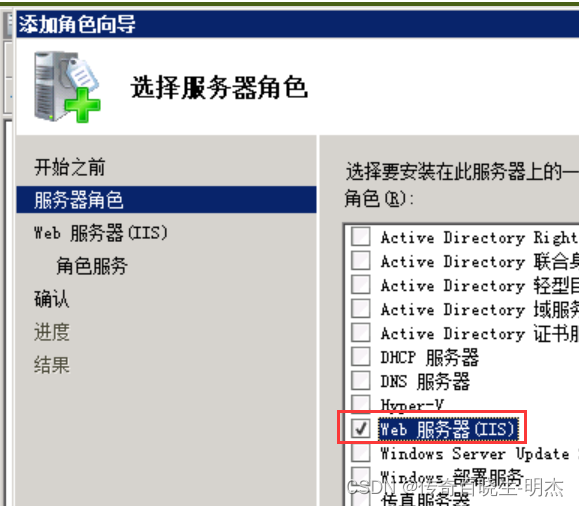
然后下一步，下一步，下一步，安装。
等几分钟，安装好
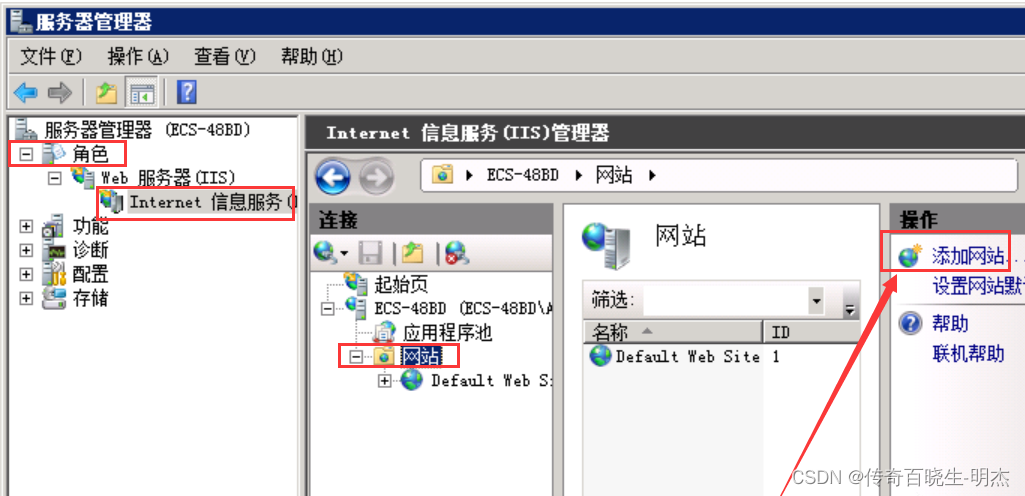
好了，现在IIS安装好，添加网站
我们这里可以使用自己的域名。已经备案的域名可以使用80端口，没备案的就换个端口
除了使用域名，如果我们域名这里为空，则可以使用IP+端口来搭建网站，IDC那边貌似必须使用IP+非80端口，
然后，把做好的网站文件解压到d:\wangzhan 就好了！
同理，搭建一个列表txt也是这样，和搭建网站毫无区别。
三：宝塔搭建网站
宝塔面板是个搭建网站的神器，可以搭建常用的静态的网站，也可以搭建论坛之类的动态网站，可以用在windows服务器，也可以用在linux服务器，他还可以在搭建网站的时候顺便把FTP搭建好，真是神器，下面以windows服务器为例
1.百度下白塔面板，下载宝塔的程序，安装
2.他会提示一个网址，账号密码
3.我们在自己电脑上，访问那个网址，输入账号密码登录
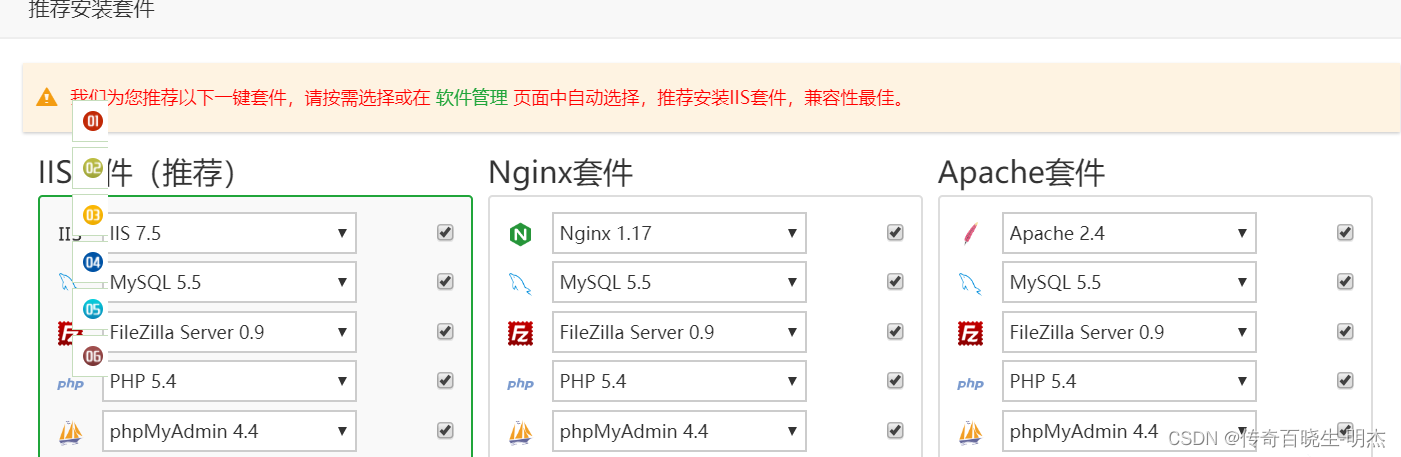
如果是干干净净的没安装IIS的服务器，用第一个，如果是以前用IIS了，就用第二个。其实这3个都差不多，都可以使用！
安装好之后，就开始搭建网站吧
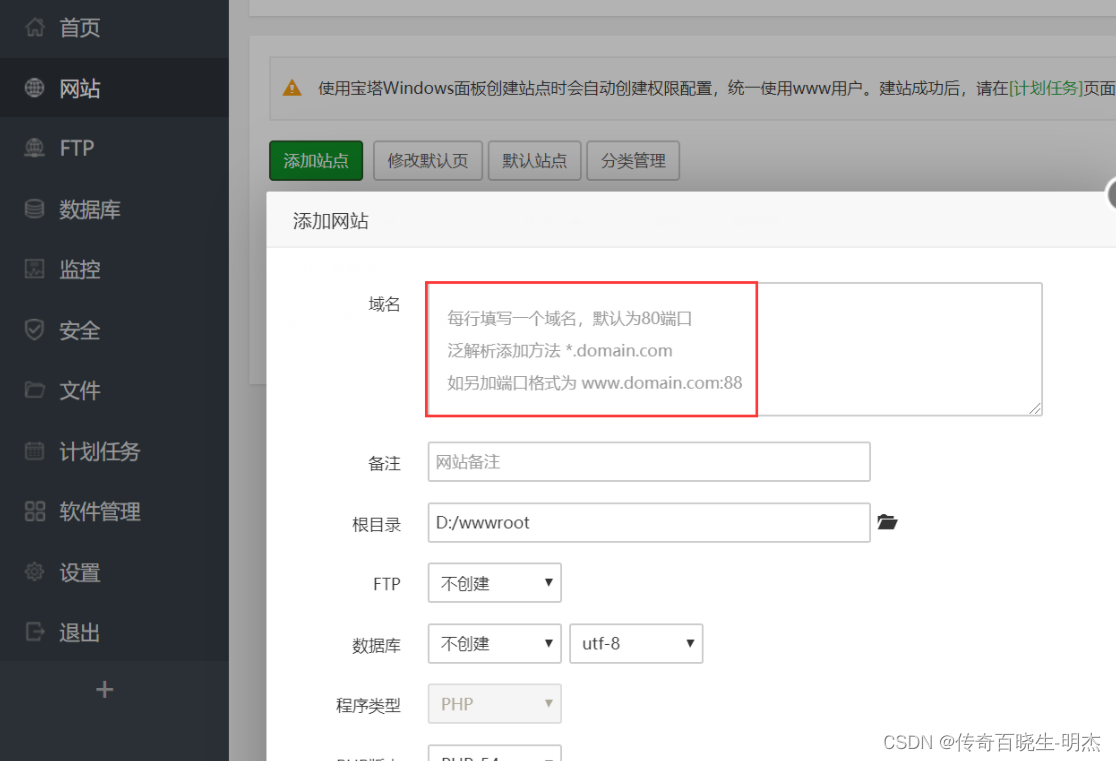
这里写域名，如果需要创建FTP就设置下，账号密码。 如果需要创建数据库就点创建，数据库一般只有论坛那些才需要创建，一般用不到。
然后创建了就OK了！ 就这么简单！比IIS好看很多
四：Linux服务器搭建网站
使用putty链接上linux服务器之后，输入宝塔的安装代码，代码去宝塔官网复制
安装成功之后，和上面三，毫无区别！
相关文章：
传奇私服搭建网站的几种方法
搭建网站的几种方法：一些人，连简单的搭建网站都不会，还要请技术帮忙，真是牛B，这里简单介绍下几种办法一：2003系统下，直接使用IIS，这个太简单了，桌面上就有IIS，…...
i.MX8MP平台开发分享（clock篇）- 各类clock的注册
专栏目录：专栏目录传送门 平台内核i.MX8MP5.15.71文章目录 1、关键数据结构1.1 clk_hw1.2 clk_hw_onecell_data2.一个clk的注册过程2.1 fixed clk2.2 pll14xx2.3 fixed factor2.4 mux2.5 composite2.6 gate1、关键数据结构 1.1 clk_hw clk_hw是描述一个时钟信息的最小单元。…...
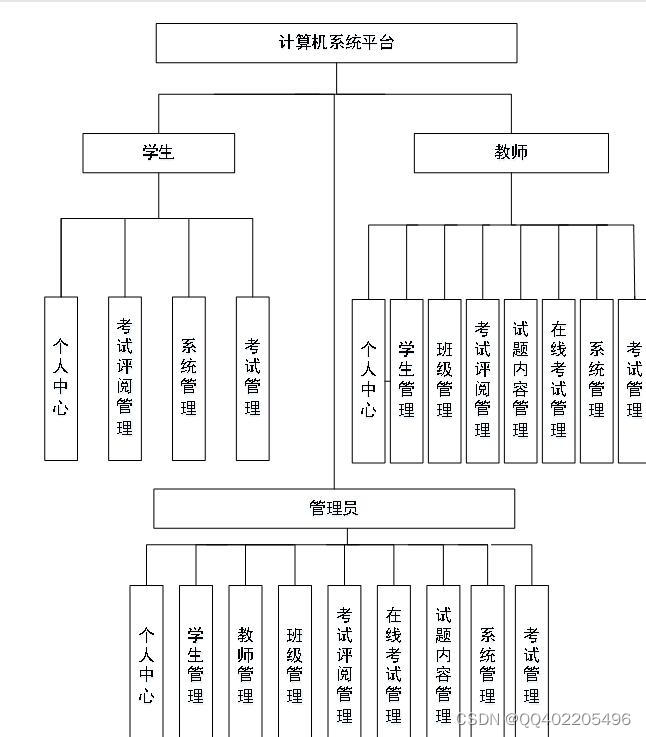
java ssm计算机系统在线考试平台idea
本系统主要包括以下功能模块学生、教师、班级、考试评阅、在线考试、试题内容、考试等模块，通过这些模块的实现能够基本满足日常计算机系统平台的操作。 本文着重阐述了计算机系统平台的分析、设计与实现，首先介绍开发系统和环境配置、数据库的设计&…...
C语言（字符串函数）
这章的内容记得引用<string.h>头文件 目录 1.strlen（） 2.strcat() 3.strncat() 4.strcmp() 5.strncmp() 6.strcpy() 7.strncpy() 8.sprintf() 8.strchr() 9.strpbrk() 10.strrchr() 11.strstr() 1.strlen（） 用于统计字符串的…...
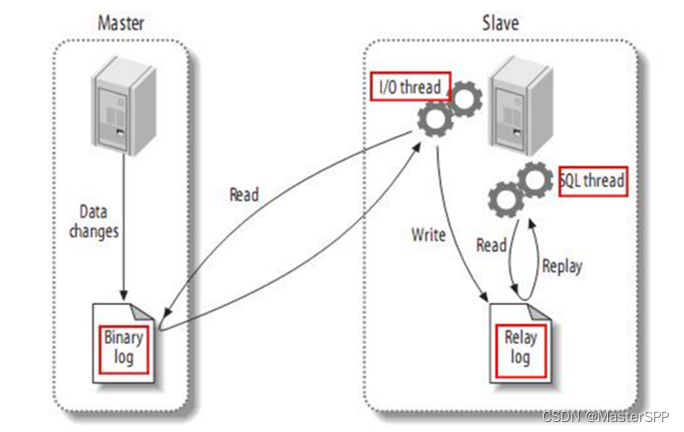
Maxwell工作流程详解
要介绍maxwell的工作原理，首先需要讲一下mysql主从复制的原理 mysql主从复制原理： 如上图，左边是master主节点，右边是slave从节点 工作流程： 1.往主节点mysql的数据库中写入数据，产生数据变化，…...
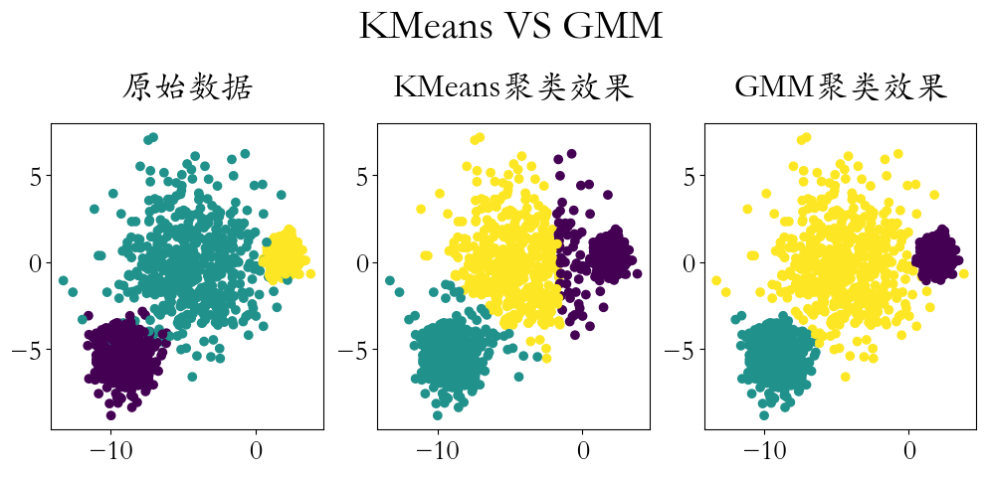
13- EM算法与GMM高斯混合 (聚类算法) (算法)
最大期望算法(EM算法) ，曾入选“数据挖掘十大算法”中，是最常见的隐变量估计方法，在机器学习中有极为广泛的用途，例如常被用来学习高斯混合模型的参数。EM算法是在概率模型中寻找参数最大似然估计或者最大后验估计的算法ÿ…...
【新】华为OD机试 - 二叉树层次遍历（Python）| 刷完获取OD招聘渠道
二叉树层次遍历 题目 有一棵二叉树 每一个节点用一个大写字母标识 最多26个节点 现有两组字母 分别表示后序遍历（左孩子指向右孩子指向父节点） 和中序遍历（左孩子指向父节点指向右孩子） 请输出层次遍历的结果 输入 输入为两个字符串 分别为二叉树的后序遍历和中序遍历结…...
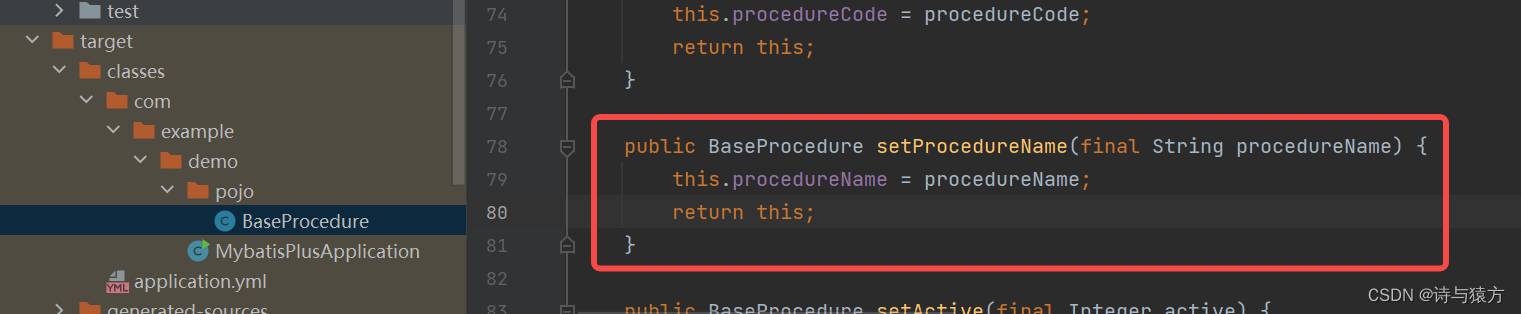
工作记录------@Accessors(chain = true)引起的BUG，Excel导入时获取不到值
工作记录------Accessors(chain true)引起的BUG，Excel导入时获取不到值 如题所示 背景：在进行文件excel文件导入时，发现实体类获取到的属性值都为null。 框架：com.alibaba.excel 2.2.0的版本。 结论：首先说下结论 如…...
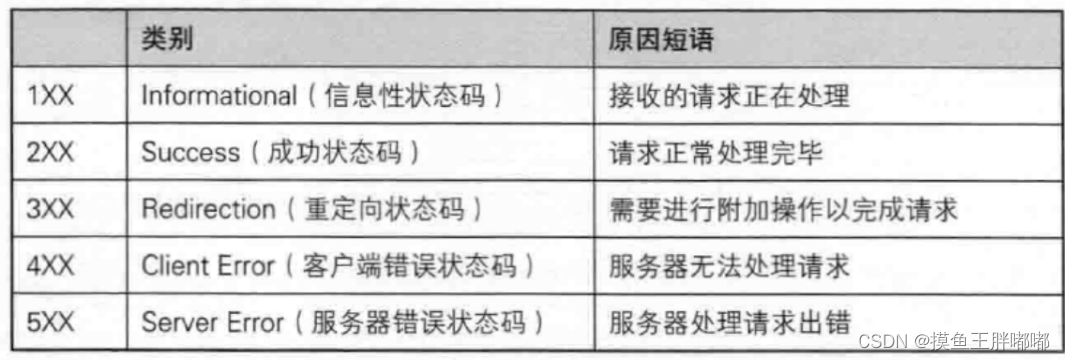
JavaEE-HTTP协议(二)
目录HTTP请求的方法GET方法POST 方法其他方法“报头”User-AgentRefererCookieHTTP响应200 OK404 Not Found403 Forbidden405 Method Not Allowed500 Internal Server Error504 Gateway Timeout302 Move temporarily301 Moved PermanentlyHTTP请求的方法 GET方法 GET 是最常用…...
代理的基本原理和多线程的基本原理
目录爬虫代理常见代理多线程并发和并行Python中的多进程和多线程爬虫时我们不到一杯茶的功夫就出现了403.打开网页一看会说您的IP访问频率太高，出现这种情况是因为网站采取了一些反爬虫措施，限制某个IP在一定时间内的请求次数，如果超过一定的…...
T38，数的递归
描述 输入一棵节点数为 n 二叉树，判断该二叉树是否是平衡二叉树。 在这里，我们只需要考虑其平衡性，不需要考虑其是不是排序二叉树 平衡二叉树（Balanced Binary Tree），具有以下性质：它是一棵空…...
QT+ OpenGL 变换
文章目录QT OpenGL变换向量的运算矩阵矩阵与向量相乘代码实现QT OpenGL 本篇完整工程见gitee:QTOpenGL 对应点的tag，由turbolove提供技术支持，您可以关注博主或者私信博主。 变换 我们需要改变物体的位置 现有解决办法（每一帧，…...
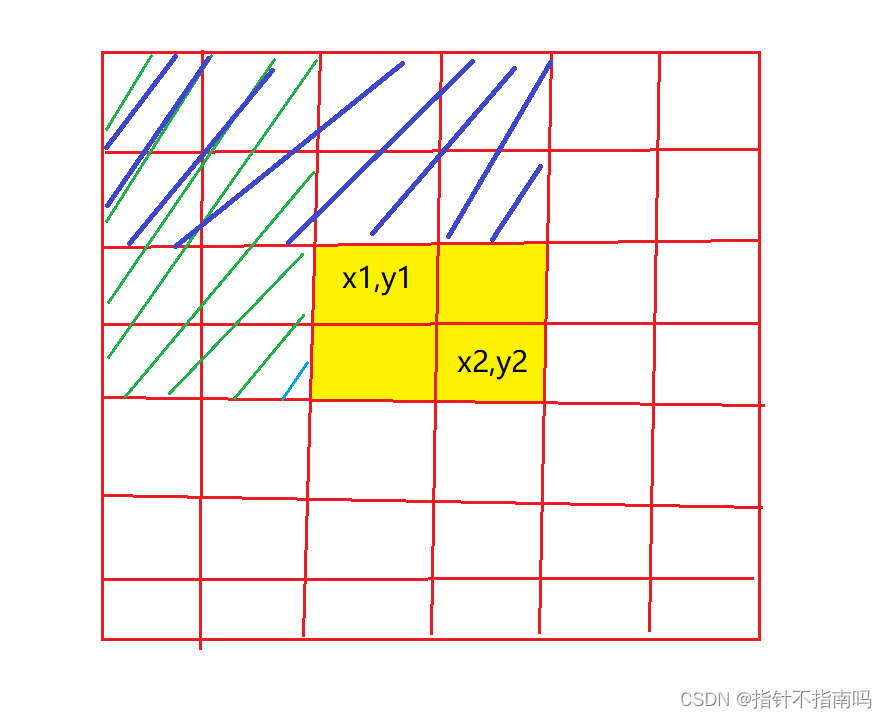
【算法】前缀和
作者：指针不指南吗 专栏：算法篇 🐾要学会在纸上打草稿，这个很重要🐾 文章目录1.什么是前缀和？2.怎么求前缀和？3.前缀和有什么用？4.进阶二维:矩阵和前缀和 主打一个记公式 1.什么是前…...
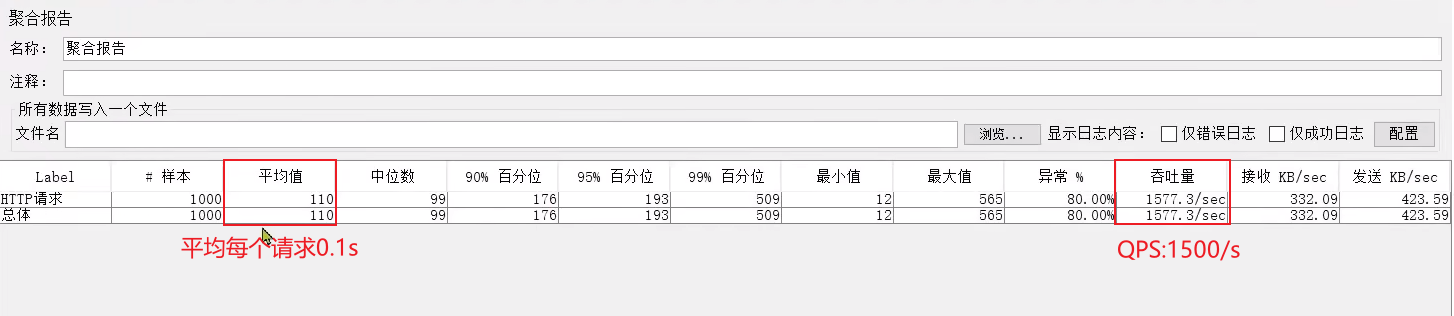
《Redis实战篇》七、Redis消息队列
7.1 Redis消息队列-认识消息队列 什么是消息队列：字面意思就是存放消息的队列。最简单的消息队列模型包括3个角色： 消息队列：存储和管理消息，也被称为消息代理（Message Broker）生产者：发送消息…...
android组件化
学习流程：1.开源最佳实践：Android平台页面路由框架ARouter-阿里云开发者社区 (aliyun.com)2.中文ARouter使用API：https://github.com/alibaba/ARouter/blob/master/README_CN.md3.看当前文档后面的代码4.这是通俗易懂的文章：https…...
华为OD机试真题Python实现【特异性双端队列】真题+解题思路+代码（20222023）
🔥系列专栏 华为OD机试（Python）真题目录汇总华为OD机试（JAVA）真题目录汇总华为OD机试（C++）真题目录汇总华为OD机试（JavaScript）真题目录汇总文章目录 🔥系列专栏题目输入输出示例一输入输出解题思路核心知识点Python 代码实现代码运行结果版权说明<...
24.架构能力
文章目录24. 架构能力24.1 Competence of Individuals: Duties, Skills, and Knowledge of Architects 个人能力：架构师的职责、技能和知识24.2 Competence of a Software Architecture Organization 软件架构组织的能力24.3 Summary 小结24.4 For Further Reading …...
前端原生 CSS 跑马灯效果，无限轮播（横竖版本，带渐变遮罩，简单实用）
一、横版跑马灯 <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><meta http-equiv"X-UA-Compatible" content"IEedge"><meta name"viewport" content"widthdevice-wid…...
4.8 注解与自定义注解
文章目录1.概述2.注解的分类2.1 JDK注解2.2 元注解2.2.1 Target ElementType…2.2.2 Retention RetentionPolicy…3 自定义注解1.概述 在注解刚出现时，曾受到过好多程序员的鄙夷，觉得这就是多此一举的操作； 但随着时间的推移，越…...
webpack 的热更新是如何做到的？原理是什么？
Hot Module Replacement，简称 HMR，在不需要刷新整个页面的同时更新模块，能够提升开发的效率和体验。热更新时只会局部刷新页面上发生了变化的模块，同时可以保留当前页面的状态，比如复选框的选中状态等。 在 webpack 中…...
XCTF-web-easyupload
试了试php，php7，pht，phtml等，都没有用 尝试.user.ini 抓包修改将.user.ini修改为jpg图片 在上传一个123.jpg 用蚁剑连接，得到flag...
基于距离变化能量开销动态调整的WSN低功耗拓扑控制开销算法matlab仿真
目录 1.程序功能描述 2.测试软件版本以及运行结果展示 3.核心程序 4.算法仿真参数 5.算法理论概述 6.参考文献 7.完整程序 1.程序功能描述 通过动态调整节点通信的能量开销，平衡网络负载，延长WSN生命周期。具体通过建立基于距离的能量消耗模型&am…...
Oracle查询表空间大小
1 查询数据库中所有的表空间以及表空间所占空间的大小 SELECTtablespace_name,sum( bytes ) / 1024 / 1024 FROMdba_data_files GROUP BYtablespace_name; 2 Oracle查询表空间大小及每个表所占空间的大小 SELECTtablespace_name,file_id,file_name,round( bytes / ( 1024 …...
LeetCode - 394. 字符串解码
题目 394. 字符串解码 - 力扣（LeetCode） 思路 使用两个栈：一个存储重复次数，一个存储字符串 遍历输入字符串： 数字处理：遇到数字时，累积计算重复次数左括号处理：保存当前状态&a…...
Linux简单的操作
ls ls 查看当前目录 ll 查看详细内容 ls -a 查看所有的内容 ls --help 查看方法文档 pwd pwd 查看当前路径 cd cd 转路径 cd .. 转上一级路径 cd 名 转换路径 …...
Vue2 第一节_Vue2上手_插值表达式{{}}_访问数据和修改数据_Vue开发者工具
文章目录 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染2. 插值表达式{{}}3. 访问数据和修改数据4. vue响应式5. Vue开发者工具--方便调试 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染 准备容器引包创建Vue实例 new Vue()指定配置项 ->渲染数据 准备一个容器,例如: …...
Java-41 深入浅出 Spring - 声明式事务的支持 事务配置 XML模式 XML+注解模式
点一下关注吧！！！非常感谢！！持续更新！！！ 🚀 AI篇持续更新中！（长期更新） 目前2025年06月05日更新到： AI炼丹日志-28 - Aud…...
在Ubuntu中设置开机自动运行（sudo）指令的指南
在Ubuntu系统中，有时需要在系统启动时自动执行某些命令，特别是需要 sudo权限的指令。为了实现这一功能，可以使用多种方法，包括编写Systemd服务、配置 rc.local文件或使用 cron任务计划。本文将详细介绍这些方法，并提供…...
Psychopy音频的使用
Psychopy音频的使用 本文主要解决以下问题： 指定音频引擎与设备；播放音频文件 本文所使用的环境： Python3.10 numpy2.2.6 psychopy2025.1.1 psychtoolbox3.0.19.14 一、音频配置 Psychopy文档链接为Sound - for audio playback — Psy…...
鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个生活电费的缴纳和查询小程序
一、项目初始化与配置 1. 创建项目 ohpm init harmony/utility-payment-app 2. 配置权限 // module.json5 {"requestPermissions": [{"name": "ohos.permission.INTERNET"},{"name": "ohos.permission.GET_NETWORK_INFO"…...