算法记录 | Day38 动态规划
对于动态规划问题,将拆解为如下五步曲
- 确定dp数组(dp table)以及下标的含义
- 确定递推公式
- dp数组如何初始化
- 确定遍历顺序
- 举例推导dp数组
509.斐波那契数
思路:
-
确定dp数组(dp table)以及下标的含义:dp[i]的定义为:第i个数的斐波那契数值是dp[i]
-
确定递推公式:状态转移方程 dp[i] = dp[i - 1] + dp[i - 2]
-
dp数组如何初始化:dp[0] = 0,dp[1] = 1
-
确定遍历顺序:从前到后遍历
-
举例推导dp数组:推导一下,当N为10的时候,dp数组应该是如下的数列:
0 1 1 2 3 5 8 13 21 34 55
class Solution:def fib(self, n: int) -> int:dp = [0 for _ in range(n+1)]if n < 1:return 0dp[0] = 0dp[1] = 1for i in range(2,n+1):dp[i] = dp[i-1] + dp[i-2]return dp[n]
70.爬楼梯
思路:
-
确定dp数组(dp table)以及下标的含义:dp[i]: 爬到第i层楼梯,有dp[i]种方法
-
确定递推公式:
dp[i] 可以有两个方向推出来。
首先是dp[i - 1],上i-1层楼梯,有dp[i - 1]种方法,那么再一步跳一个台阶不就是dp[i]了么。
还有就是dp[i - 2],上i-2层楼梯,有dp[i - 2]种方法,那么再一步跳两个台阶不就是dp[i]了么。
-
dp数组如何初始化:dp[0] = 1,dp[1] = 1
-
确定遍历顺序:从前到后遍历
-
举例推导dp数组:
class Solution:def climbStairs(self, n: int) -> int:dp = [0 for _ in range(n+1)]if n == 0:return 0dp[0] = 1dp[1] = 1for i in range(2,n+1):dp[i] = dp[i-1] + dp[i-2]return dp[n]
746.使用最小花费爬楼梯
思路:
-
确定dp数组(dp table)以及下标的含义:dp[i]爬到楼顶的花费
-
确定递推公式:
dp[i - 1],到上i-1层楼梯,花费dp[i - 1],i-1到i花费dp[i - 1]+cost[i-1]
dp[i - 2],上i-2层楼梯,花费dp[i - 2],i-2到i花费dp[i - 2]+cost[i-2]
dp [i] = min(dp[i - 1]+cost[i-1],dp[i - 2]+cost[i-2])
-
dp数组如何初始化:dp[0] = 0,dp[1] = 0
**注意:**题目描述中明确说了 “你可以选择从下标为 0 或下标为 1 的台阶开始爬楼梯。” 也就是说 从 到达 第 0 个台阶是不花费的,但从 第0 个台阶 往上跳的话,需要花费 cost[0]。
-
确定遍历顺序:从前到后遍历
-
举例推导dp数组:
cost = [1, 100, 1, 1, 1, 100, 1, 1, 100, 1] ,来模拟一下dp数组的状态变化,如下:
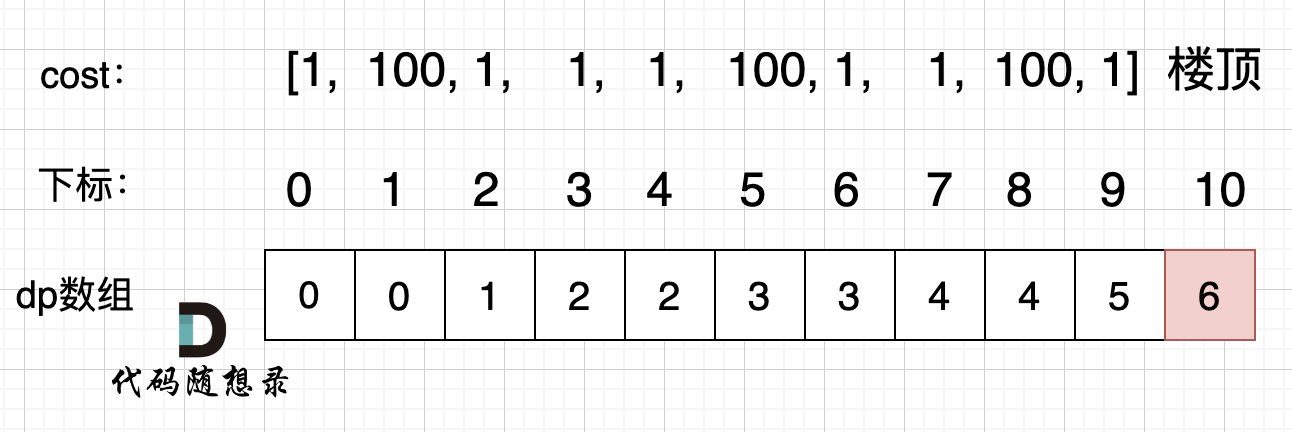
class Solution:def minCostClimbingStairs(self, cost: List[int]) -> int:n = len(cost) dp = [0 for _ in range(n+1)]if n < 1:return 0dp[0] = 0dp[1] = 0for i in range(2, n+1):dp[i] = min(dp[i-1]+cost[i-1],dp[i-2]+cost[i-2])return dp[n]
相关文章:

算法记录 | Day38 动态规划
对于动态规划问题,将拆解为如下五步曲 确定dp数组(dp table)以及下标的含义确定递推公式dp数组如何初始化确定遍历顺序举例推导dp数组 509.斐波那契数 思路: 确定dp数组(dp table)以及下标的含义&#x…...
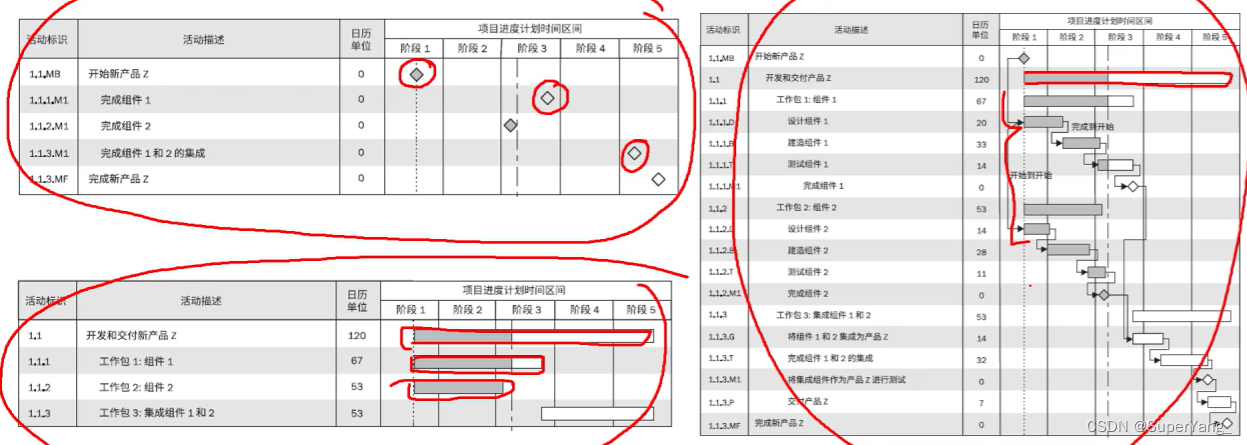
PMP项目管理-[第六章]进度管理
进度管理知识体系: 规划进度管理: 定义活动: 排列活动顺序: 估算活动持续时间: 制定进度计划: 6.1 规划进度管理 定义:为规划、编制、管理、执行和控制项目进度而制定政策、程序和文档的过程 作…...

Python变量
一、变量的定义 变量名的命名规范:变量名是标识符的一种,变量名不能随便起,要遵守 Python 标识符命名规范。 ## 常用的命名规范有以下几种: 1. 变量名为单个单词的话全部小写 name "张三" 2. 多个单词组成的话&#…...

准备换工作的看过来~
大家好,最近有不少小伙伴在后台留言,得准备面试了,又不知道从何下手!为了帮大家节约时间,特意准备了一份面试相关的资料,内容非常的全面,真的可以好好补一补,希望大家在都能拿到理想…...
免费AI人工智能在线写作伪原创-百度ai自动写文章
免费伪原创洗稿工具 免费伪原创洗稿工具现在终于推出了!你是否在写作的时候,经常因为缺乏灵感而苦恼?或者,你在撰写文章的时候,发现自己的语言表述不够丰富,缺乏变化,语句重复率太高?…...
)
互联网摸鱼日报(2023-04-21)
互联网摸鱼日报(2023-04-21) InfoQ 热门话题 3年不用云能节省4亿美元!想知道我们为什么敢不用AWS吗? 华为周红:通过行业大模型促进AI价值创造 建设业务规划、交付和反馈闭环| BizDevOps 公开课 云原生时…...
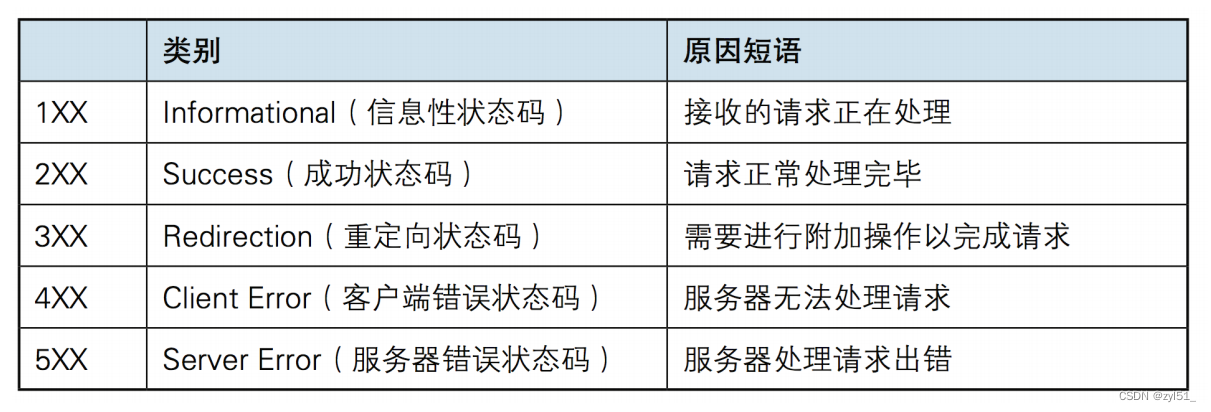
5.3、web服务器简介HTTP协议
代码地址 5.3、web服务器简介HTTP协议 1.Web-Server(网页服务器)2.HTTP协议(应用层的协议)①简介②概述③工作原理④HTTP请求报文格式⑤HTTP响应报文格式⑥HTTP请求方法⑦HTTP状态码 1.Web-Server(网页服务器) 一个 Web Server …...

【观察】华为:新一代楼宇网络,使能绿建智慧化
“碳达峰”、“碳中和”目标是我国生态文明建设和高质量可持续发展的重要战略安排,将推动全社会加速向绿色低碳转型。作为全球既有建筑和每年新建建筑量最大的国家,大力发展绿色建筑对中国全方位迈向低碳社会、实现高质量发展具有重要意义。 《“十四五”…...

【C# .NET】chapter 13 使用多任务改进性能和可扩展性
目录 一、物理内存和虚拟内存使用(Recorder 类) 二、 对比 string的“”操作与stringbuilder 操作 的处理效率,内存消耗情况, 三、异步运行任务、三种启动任务方法、将上一任务方法处理结果作为参数传给下一任务方法 四、嵌套…...

CA(证书颁发机构)
CA 根证书路径/csk-rootca/csk-ca.pem; ~ 签发数字证书,颁发者信息:(仅包含如下信息) C CN ST China L BeiJing O skills OU Operations Departments CN CSK Global Root CA 1.修改证书的路径以及相关配置 vi /etc/pki/tls/op…...

辛弃疾最有代表性的十首词
辛弃疾的词,风格多样,题材广阔,几乎涉及到生活中的各个方面,从爱国情怀到日常生活,甚至连戒酒这种事都能写入词中。辛弃疾也是两宋词人中,存词最多的作家之一,现存的六百多首作品。 辛弃疾的词…...
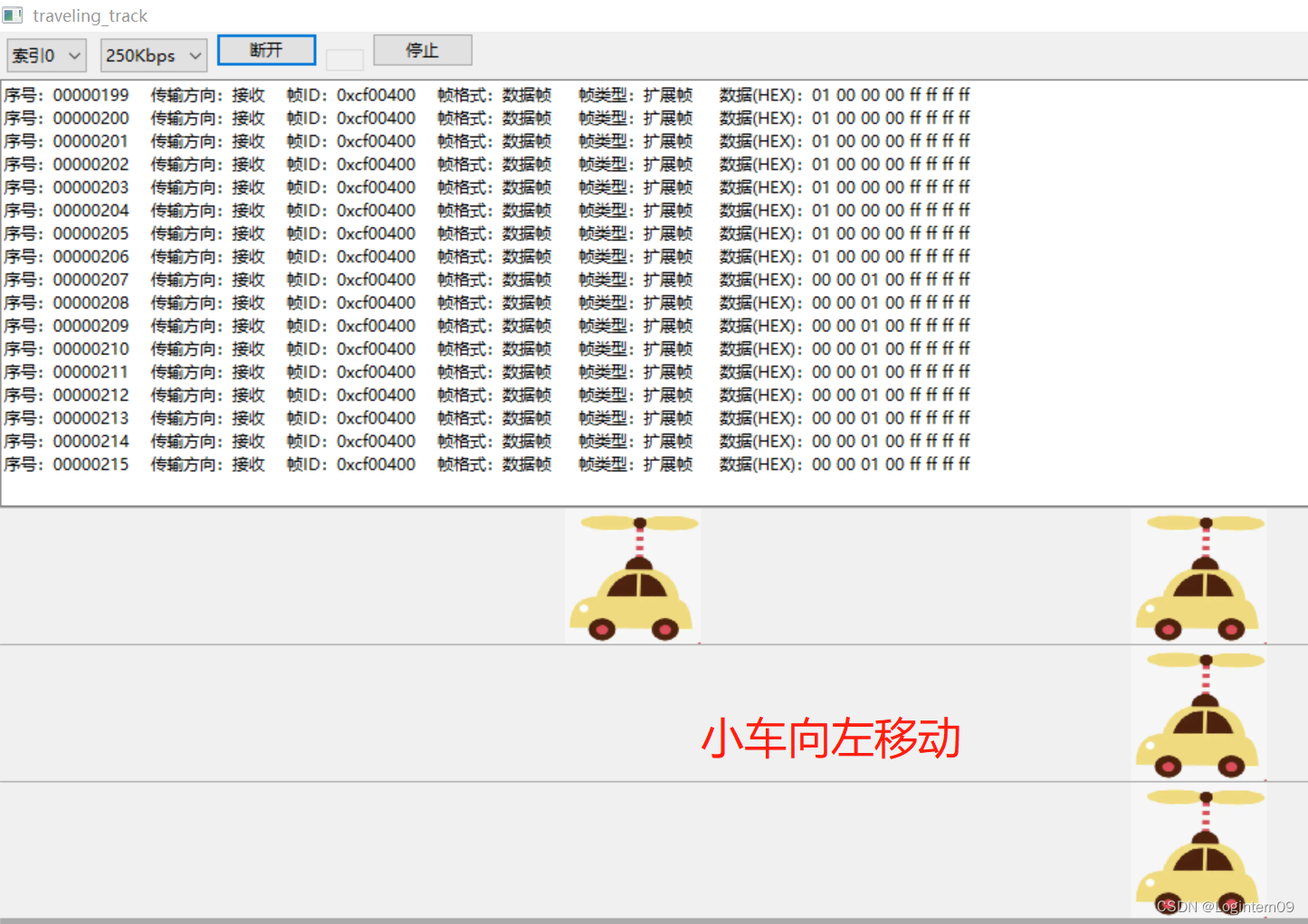
MC9S12G128开发板—实现按键发送CAN报文指示小车移动功能
实验环境:MC9S12G128开发板 基本功能:控制开发板上的按键,模拟车辆移动的上下左右四个方位,通过can通信告诉上位机界面,车辆轨迹的移动方位。 1. 1939报文发送的示例代码 MC9S12G128开发板1939协议发送can报文数据的…...
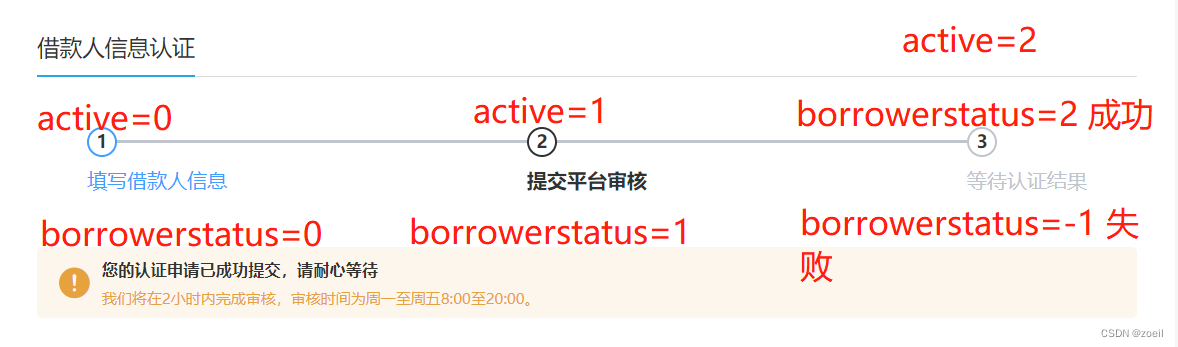
尚融宝22-提交借款申请
目录 一、需求介绍 二、图片上传 (一)前端页面 (二)实现图片上传 三、数据字典展示 (一)后端 (二)前端 四、表单信息提交 (一)后端 1、VO对象&…...
机器学习在生态、环境经济学中的实践技术应用及论文写作
近年来,人工智能领域已经取得突破性进展,对经济社会各个领域都产生了重大影响,结合了统计学、数据科学和计算机科学的机器学习是人工智能的主流方向之一,目前也在飞快的融入计量经济学研究。表面上机器学习通常使用大数据…...

Android硬件通信之 WIFI通信
一,简介 1.1 随着网络的普及和通信技术的发展,网络的传输速度也越来越快,wifi技术也还成为手机设备最基本的配置。我们可以通过wifi实现手机与手机之前的信息传输,当然也可以与任意一台有wifi模块的其它设备传输。 1.2 wifi与蓝…...
面试官:“请描述一下Android系统的启动流程”
作者:OpenGL 前言 什么是Android启动流程呢?其实指的就是我们Android系统从按下电源到显示界面的整个过程。 当我们把手机充好电,按下电源,手机会弹出相应启动界面,在等了一段时间之后,会弹出我们熟悉的主…...

k8s delete node 后 重启kubelet会自己加入到集群 ?
原因 当执行kubectl delete node命令时,Kubernetes API服务器会收到该节点的删除请求,并将其从集群中删除。此时,kubelet服务在该节点上仍然在运行,但已经不再与集群通信。 当您重启kubelet服务时,它会重新向API服务…...

REXROTH液压方向阀安装须知
安装规程 阀安装到系统之前,应该对照订货型号比较其型号说明。 确认阀的连接表面和底板无水分,没有油。 - 清洁: ‧ 安装元件时,确认工业阀和周围干净 ‧ 油箱须密闭,以防止外部污染 ‧ 安装之前&…...

【数据结构实验】哈夫曼树
【数据结构实验】哈夫曼树 简介: 为一个信息收发站编写一个哈夫曼码的编/译码系统。文末贴出了源代码。 需求分析 完整的系统需要具备完整的功能,包含初始化、编码、译码、印代码文件和印哈夫曼树,因此需要进行相应的文件操作进行配合。哈…...
浏览器不好用?插件来帮忙
一、目的 浏览器本身具备的功能并不完善,不同的用户可以为自己浏览器增加想要功能,使得浏览器更能符合自己的需求,提高浏览器使用的舒适度 二、推荐插件 AdblockPlus LastPass(密码记录,全平台通用) Dar…...
:手搓截屏和帧率控制)
Python|GIF 解析与构建(5):手搓截屏和帧率控制
目录 Python|GIF 解析与构建(5):手搓截屏和帧率控制 一、引言 二、技术实现:手搓截屏模块 2.1 核心原理 2.2 代码解析:ScreenshotData类 2.2.1 截图函数:capture_screen 三、技术实现&…...

论文浅尝 | 基于判别指令微调生成式大语言模型的知识图谱补全方法(ISWC2024)
笔记整理:刘治强,浙江大学硕士生,研究方向为知识图谱表示学习,大语言模型 论文链接:http://arxiv.org/abs/2407.16127 发表会议:ISWC 2024 1. 动机 传统的知识图谱补全(KGC)模型通过…...
)
【服务器压力测试】本地PC电脑作为服务器运行时出现卡顿和资源紧张(Windows/Linux)
要让本地PC电脑作为服务器运行时出现卡顿和资源紧张的情况,可以通过以下几种方式模拟或触发: 1. 增加CPU负载 运行大量计算密集型任务,例如: 使用多线程循环执行复杂计算(如数学运算、加密解密等)。运行图…...

拉力测试cuda pytorch 把 4070显卡拉满
import torch import timedef stress_test_gpu(matrix_size16384, duration300):"""对GPU进行压力测试,通过持续的矩阵乘法来最大化GPU利用率参数:matrix_size: 矩阵维度大小,增大可提高计算复杂度duration: 测试持续时间(秒&…...

稳定币的深度剖析与展望
一、引言 在当今数字化浪潮席卷全球的时代,加密货币作为一种新兴的金融现象,正以前所未有的速度改变着我们对传统货币和金融体系的认知。然而,加密货币市场的高度波动性却成为了其广泛应用和普及的一大障碍。在这样的背景下,稳定…...

鸿蒙DevEco Studio HarmonyOS 5跑酷小游戏实现指南
1. 项目概述 本跑酷小游戏基于鸿蒙HarmonyOS 5开发,使用DevEco Studio作为开发工具,采用Java语言实现,包含角色控制、障碍物生成和分数计算系统。 2. 项目结构 /src/main/java/com/example/runner/├── MainAbilitySlice.java // 主界…...

sipsak:SIP瑞士军刀!全参数详细教程!Kali Linux教程!
简介 sipsak 是一个面向会话初始协议 (SIP) 应用程序开发人员和管理员的小型命令行工具。它可以用于对 SIP 应用程序和设备进行一些简单的测试。 sipsak 是一款 SIP 压力和诊断实用程序。它通过 sip-uri 向服务器发送 SIP 请求,并检查收到的响应。它以以下模式之一…...

springboot整合VUE之在线教育管理系统简介
可以学习到的技能 学会常用技术栈的使用 独立开发项目 学会前端的开发流程 学会后端的开发流程 学会数据库的设计 学会前后端接口调用方式 学会多模块之间的关联 学会数据的处理 适用人群 在校学生,小白用户,想学习知识的 有点基础,想要通过项…...

招商蛇口 | 执笔CID,启幕低密生活新境
作为中国城市生长的力量,招商蛇口以“美好生活承载者”为使命,深耕全球111座城市,以央企担当匠造时代理想人居。从深圳湾的开拓基因到西安高新CID的战略落子,招商蛇口始终与城市发展同频共振,以建筑诠释对土地与生活的…...

多模态图像修复系统:基于深度学习的图片修复实现
多模态图像修复系统:基于深度学习的图片修复实现 1. 系统概述 本系统使用多模态大模型(Stable Diffusion Inpainting)实现图像修复功能,结合文本描述和图片输入,对指定区域进行内容修复。系统包含完整的数据处理、模型训练、推理部署流程。 import torch import numpy …...
