k8s delete node 后 重启kubelet会自己加入到集群 ?
原因
当执行kubectl delete node命令时,Kubernetes API服务器会收到该节点的删除请求,并将其从集群中删除。此时,kubelet服务在该节点上仍然在运行,但已经不再与集群通信。
当您重启kubelet服务时,它会重新向API服务器注册节点,并告知API服务器该节点的状态。如果该节点之前被删除并且现在重新启动,kubelet服务将向API服务器发送一个“NodeReady”消息,表明该节点已准备好接受Pod的调度。API服务器将更新该节点的状态,并将其重新添加到集群中。因此,重启kubelet服务后,它会自动加入到集群中。
正确删除 Kubernetes 集群中的节点,应该按照如下步骤进行:
-
从节点上删除所有运行的Pod,以确保没有任何应用程序在该节点上运行。
-
从 Kubernetes 集群中删除该节点,可以使用以下命令:
kubectl delete node <node-name>其中,
<node-name>是要删除的节点的名称。 -
在节点上停止 kubelet 服务,可以使用以下命令:
systemctl stop kubelet -
在节点上清除所有 Kubernetes 组件的数据,可以使用以下命令:
rm -rf /var/lib/kubelet/* rm -rf /etc/kubernetes/*这将删除 kubelet、kube-proxy 和其他 Kubernetes 组件在节点上存储的所有数据。
-
最后,从节点上删除 kubelet 二进制文件,可以使用以下命令:
rm -f /usr/bin/kubelet这将删除 kubelet 二进制文件,确保该节点不会再次加入 Kubernetes 集群。
按照上述步骤操作可以有效地从 Kubernetes 集群中删除节点。
相关文章:

k8s delete node 后 重启kubelet会自己加入到集群 ?
原因 当执行kubectl delete node命令时,Kubernetes API服务器会收到该节点的删除请求,并将其从集群中删除。此时,kubelet服务在该节点上仍然在运行,但已经不再与集群通信。 当您重启kubelet服务时,它会重新向API服务…...

REXROTH液压方向阀安装须知
安装规程 阀安装到系统之前,应该对照订货型号比较其型号说明。 确认阀的连接表面和底板无水分,没有油。 - 清洁: ‧ 安装元件时,确认工业阀和周围干净 ‧ 油箱须密闭,以防止外部污染 ‧ 安装之前&…...

【数据结构实验】哈夫曼树
【数据结构实验】哈夫曼树 简介: 为一个信息收发站编写一个哈夫曼码的编/译码系统。文末贴出了源代码。 需求分析 完整的系统需要具备完整的功能,包含初始化、编码、译码、印代码文件和印哈夫曼树,因此需要进行相应的文件操作进行配合。哈…...
浏览器不好用?插件来帮忙
一、目的 浏览器本身具备的功能并不完善,不同的用户可以为自己浏览器增加想要功能,使得浏览器更能符合自己的需求,提高浏览器使用的舒适度 二、推荐插件 AdblockPlus LastPass(密码记录,全平台通用) Dar…...

Qt Quick - 容器控件综述
Qt Quick - 容器控件综述 一、概述二、ApplicationWindow Control三、Frame Control四、GroupBox Control五、Page Control六、Pane Control七、ScrollView Control八、StackView Control九、SwipeView Control十、TabBarControl十一、ToolBar控件 一、概述 Qt Quick Controls…...

面试题30天打卡-day06
1、什么是反射机制?说说反射机制的优缺点、应用场景? 反射机制:Java的反射机制是在运行状态,对于任意一个类,都能够动态的获得这个类的属性和方法;对于一个对象,都能动态的调用它当中的方法和属…...

Spring Boot的基础使用和< artifactId>spring-boot-maven-plugin</ artifactId>爆红的处理
Spring Boot的基础使用和< artifactId>spring-boot-maven-plugin</ artifactId>爆红的处理 Spring Boot概述 微服务概述 微服务Microservices是一种软件架构风格,他是以专注于单一责任与功能的小型功能区块Small Building Blocks 为基础,…...

项目管理中的必不可少的强大工具有哪些?
在项目管理中,我们总是想寻求一套功能强大的工具,来满足我们多样化的需求。但往往事与愿违,这样强大的工具总是费用高,操作复杂,需安装多个插件。下面,我就给大家推荐一款项目管理软件 ~Zoho Projects&…...

嵌入式学习笔记——SPI通信的应用
SPI通信的应用 前言屏幕分类1.3OLED概述驱动芯片框图原理图通信时序显示的方式页地址、列地址初始化指令 程序设计初始化代码初始化写数据与写命令清屏函数 初始化代码字符显示函数 总结 前言 上一篇中介绍了STM32的SPI通信,并根据框图和寄存器进行了SPI通信的初始…...

.Net下企业应用系统架构构建心得
在开始架构设计之前,需要了解一下架构是什么,按照IEEE标准的定义是: Architecture 是一个系统的基本组织,它蕴含于系统的组件中、组件之间的相互关系中、组件与环境的相互关系中、以及呈现于其设计和演进的原则中。 (The embodied…...

【社区图书馆】关于Mybatis原理学习的读后感
1、为什么会看原理书籍 Mybatis是我们Java后端开发中的主流ORM框架,基本都会在工作中用到。所以,是既熟悉,又陌生。熟悉是因为一直都在使用,而陌生则是对于其内部原理还不够深入。刚好近期的工作中,又遇到了一个需求&a…...
C++ Primer阅读笔记--表达式和运算符的使用
1--左值和右值 C 的表达式有右值(rvalue, are-value)和左值(lvalue, ell-value)两个形式;当一个对象被用作右值时,使用的是对象的值(内容);当对象被用作左值时࿰…...

npm install xxx的执行过程及示例
当你在终端中执行npm install xxx命令时,npm会执行以下步骤来安装软件包: 检查本地npm缓存中是否有该软件包。 如果本地npm缓存中已经存在该软件包,npm将直接从缓存中提取软件包并安装。这将显著加快安装速度,因为npm无需从网络下…...
excel数据分析比赛
基础 sql:百度网盘 请输入提取码 excel函数 <...

Git使用GitHub说明
GitHub为公网代码托管仓库,Git可以将本地仓库推送到GitHub管理。 步骤:1、注册GitHub账号 2、创建仓库(会得到一个仓库地址) 3、推送本地仓库 git remote add origin https://github.com/jianshengchuanqi/xuesezhanjiang.git…...
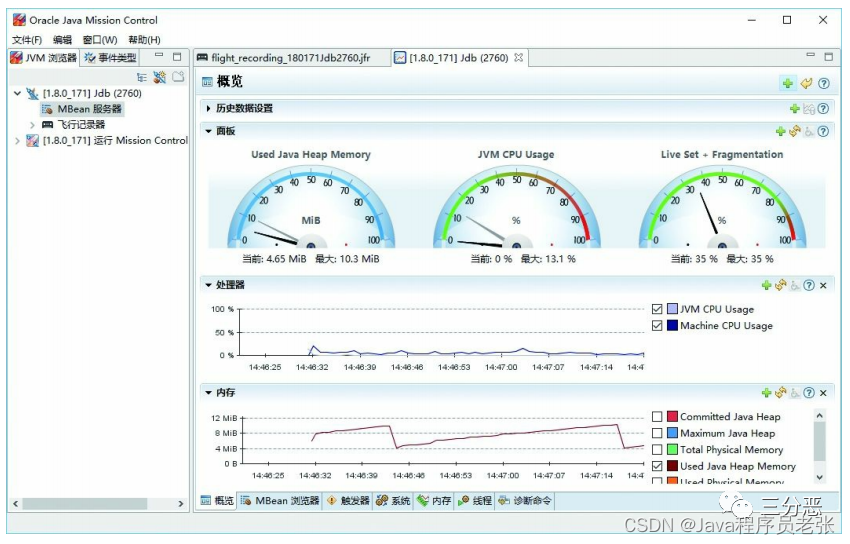
这些不可不知的JVM知识
JVM是面试中必问的部分,本文通过思维导图以面向面试的角度整理JVM中不可不知的知识。 先上图: JVM必备知识 1、JVM基本概念 1.1、JVM是什么 JVM 的全称是 「Java Virtual Machine」,也就是我们耳熟能详的 Java 虚拟机。 JVM具备着计算机的…...

基于RK3568的Linux驱动开发——GPIO知识点(一)
authordaisy.skye的博客_CSDN博客-Qt,嵌入式,Linux领域博主系列基于RK3568的Linux驱动开发—— GPIO知识点(二)_daisy.skye的博客-CSDN博客 gpio bank RK3568 有 5 组 GPIO bank:GPIO0~GPIO4,每组又以 A0-A7、B0-B7、 C0-C7、 D0…...
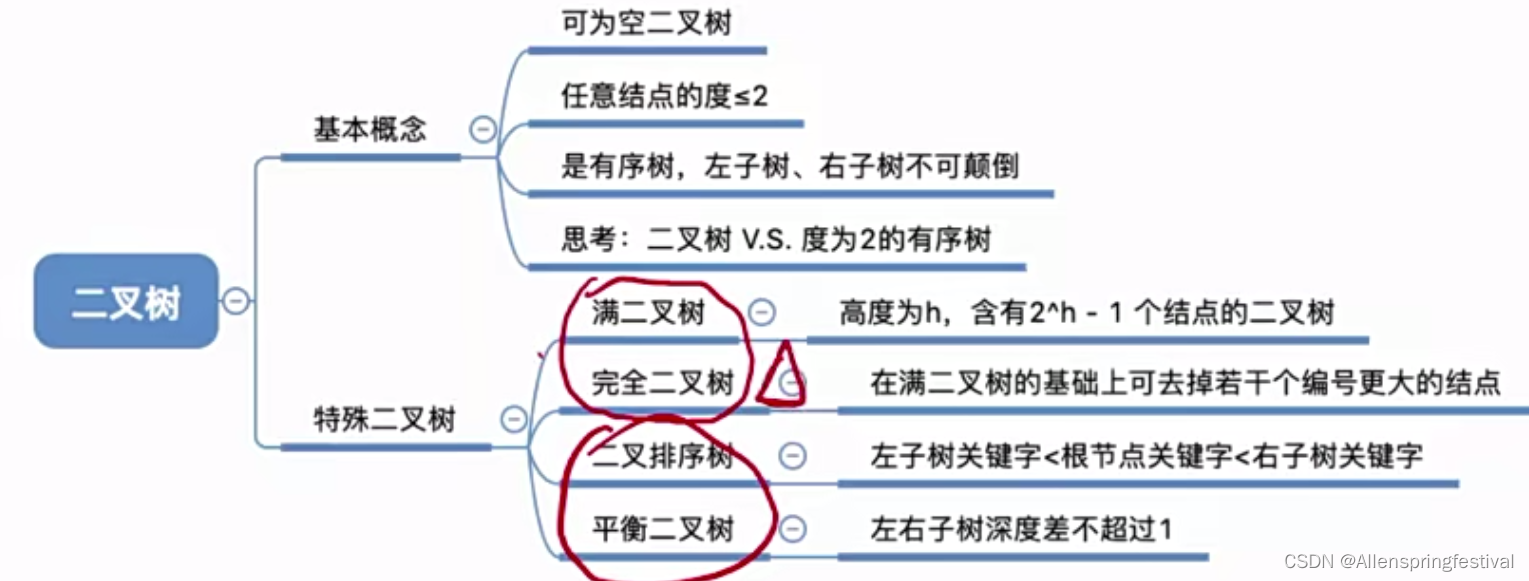
5.2.1二叉树的定义和基本术语
二叉树的基本概念: 二叉树是递归定义的二叉树 下面我们来看几个特殊的二叉树: 特点: 1)只有最后一层有叶子节点 2)不存在度为1的结点 3)按层序从1开始编号,结点i的左孩子为2i,右孩…...

动态组件、keep-alive的使用及自定义指令
目录 1. 动态组件 2.如何实现动态组件渲染 3. 使用keep-alive保持状态 4. keep-alive对应的生命周期函数 5. keep-alive的include属性 自定义指令 1.什么是自定义指令 2. 自定义指令的分类 3. 私有自定义指令 4. update函数 5. 函数简写 全局自定义指令: …...
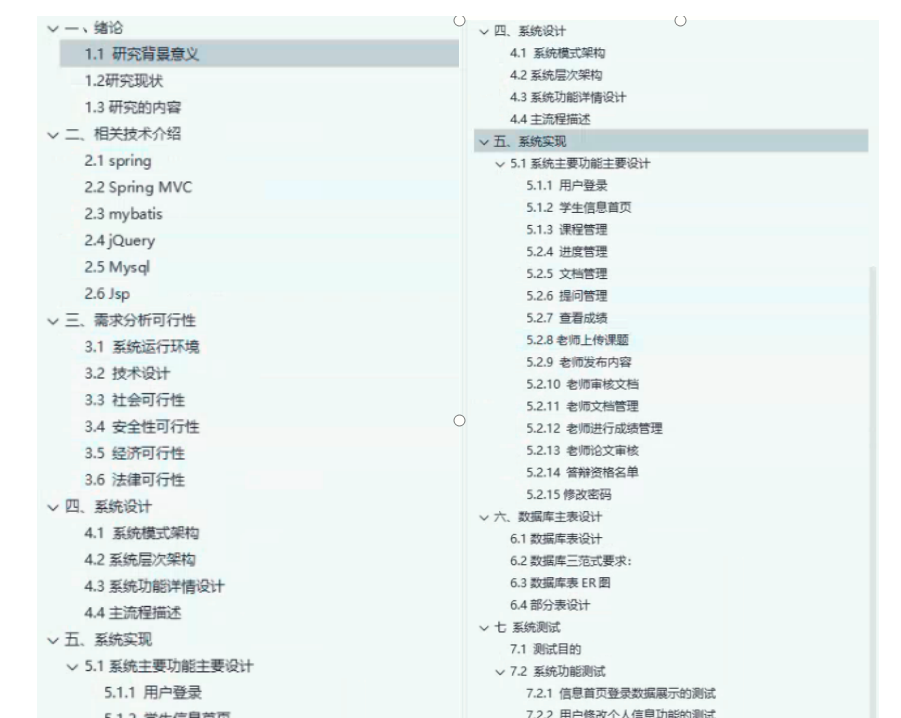
基于JavaSpringMVC+Mybatis+Jquery高校毕业设计管理系统设计和实现
基于JavaSpringMVCMybatisJquery高校毕业设计管理系统设计和实现 博主介绍:5年java开发经验,专注Java开发、定制、远程、指导等,csdn特邀作者、专注于Java技术领域 作者主页 超级帅帅吴 Java项目精品实战案例《500套》 欢迎点赞 收藏 ⭐留言 文末获取源码…...

网络编程(Modbus进阶)
思维导图 Modbus RTU(先学一点理论) 概念 Modbus RTU 是工业自动化领域 最广泛应用的串行通信协议,由 Modicon 公司(现施耐德电气)于 1979 年推出。它以 高效率、强健性、易实现的特点成为工业控制系统的通信标准。 包…...

高等数学(下)题型笔记(八)空间解析几何与向量代数
目录 0 前言 1 向量的点乘 1.1 基本公式 1.2 例题 2 向量的叉乘 2.1 基础知识 2.2 例题 3 空间平面方程 3.1 基础知识 3.2 例题 4 空间直线方程 4.1 基础知识 4.2 例题 5 旋转曲面及其方程 5.1 基础知识 5.2 例题 6 空间曲面的法线与切平面 6.1 基础知识 6.2…...

学习STC51单片机31(芯片为STC89C52RCRC)OLED显示屏1
每日一言 生活的美好,总是藏在那些你咬牙坚持的日子里。 硬件:OLED 以后要用到OLED的时候找到这个文件 OLED的设备地址 SSD1306"SSD" 是品牌缩写,"1306" 是产品编号。 驱动 OLED 屏幕的 IIC 总线数据传输格式 示意图 …...

高危文件识别的常用算法:原理、应用与企业场景
高危文件识别的常用算法:原理、应用与企业场景 高危文件识别旨在检测可能导致安全威胁的文件,如包含恶意代码、敏感数据或欺诈内容的文档,在企业协同办公环境中(如Teams、Google Workspace)尤为重要。结合大模型技术&…...

python如何将word的doc另存为docx
将 DOCX 文件另存为 DOCX 格式(Python 实现) 在 Python 中,你可以使用 python-docx 库来操作 Word 文档。不过需要注意的是,.doc 是旧的 Word 格式,而 .docx 是新的基于 XML 的格式。python-docx 只能处理 .docx 格式…...

SpringTask-03.入门案例
一.入门案例 启动类: package com.sky;import lombok.extern.slf4j.Slf4j; import org.springframework.boot.SpringApplication; import org.springframework.boot.autoconfigure.SpringBootApplication; import org.springframework.cache.annotation.EnableCach…...

Pinocchio 库详解及其在足式机器人上的应用
Pinocchio 库详解及其在足式机器人上的应用 Pinocchio (Pinocchio is not only a nose) 是一个开源的 C 库,专门用于快速计算机器人模型的正向运动学、逆向运动学、雅可比矩阵、动力学和动力学导数。它主要关注效率和准确性,并提供了一个通用的框架&…...

【无标题】路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论
路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论 一、传统路径模型的根本缺陷 在经典正方形路径问题中(图1): mermaid graph LR A((A)) --- B((B)) B --- C((C)) C --- D((D)) D --- A A -.- C[无直接路径] B -…...

力扣热题100 k个一组反转链表题解
题目: 代码: func reverseKGroup(head *ListNode, k int) *ListNode {cur : headfor i : 0; i < k; i {if cur nil {return head}cur cur.Next}newHead : reverse(head, cur)head.Next reverseKGroup(cur, k)return newHead }func reverse(start, end *ListNode) *ListN…...

Webpack性能优化:构建速度与体积优化策略
一、构建速度优化 1、升级Webpack和Node.js 优化效果:Webpack 4比Webpack 3构建时间降低60%-98%。原因: V8引擎优化(for of替代forEach、Map/Set替代Object)。默认使用更快的md4哈希算法。AST直接从Loa…...
