「计算机控制系统」6. 直接设计法
特殊类型系统的最小拍无差设计
一般系统的最小拍无差设计
最小拍控制器的工程化改进
Dahlin算法
文章目录
- 特殊类型系统的最小拍无差设计
- 理论分析
- 典型输入函数的最小拍无差系统
- 一般系统的最小拍无差设计
- 有波纹最小拍无差设计
- 无波纹最小拍无差设计
- 最小拍控制器的工程化改进
- 针对输入信号类型敏感问题
- 针对模型参数变化敏感问题
- Dahlin算法
- 使用Dahlin算法设计控制器
- 振铃及其消除
直接设计和模拟设计法相对,是指直接基于计算机控制系统进行设计。
典型的计算机控制系统如图:
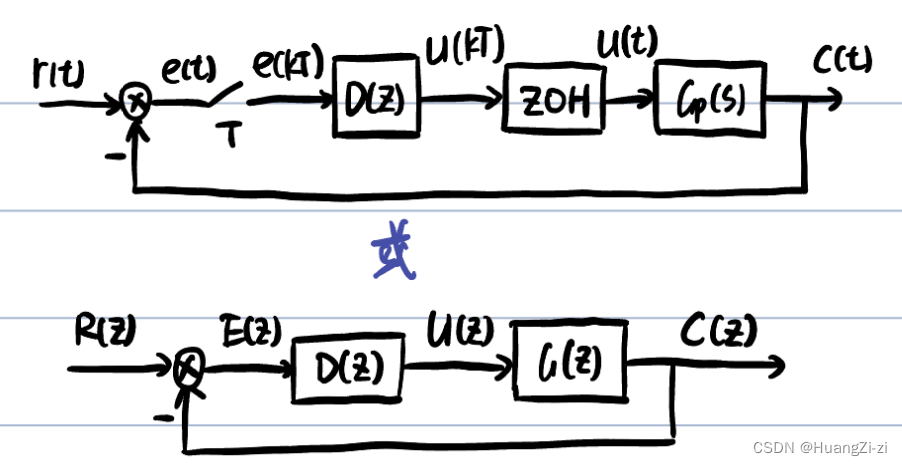
直接设计法的步骤:
- 根据控制系统性能指标或者其他约束条件,确定所需的闭环脉冲传函 ϕ ( z ) \phi(z) ϕ(z)
- 确定数字控制器的脉冲传函:

- 编写控制算法程序
特殊类型系统的最小拍无差设计
- 特殊类型系统:
(1)广义被控对象的脉冲传函 G ( z ) G(z) G(z)稳定
(2) G ( z ) G(z) G(z)中不含纯延时环节 - 最小拍无差:
在最少的几个采样周期内达到在采样时刻的输入和输出无误差。
理论分析
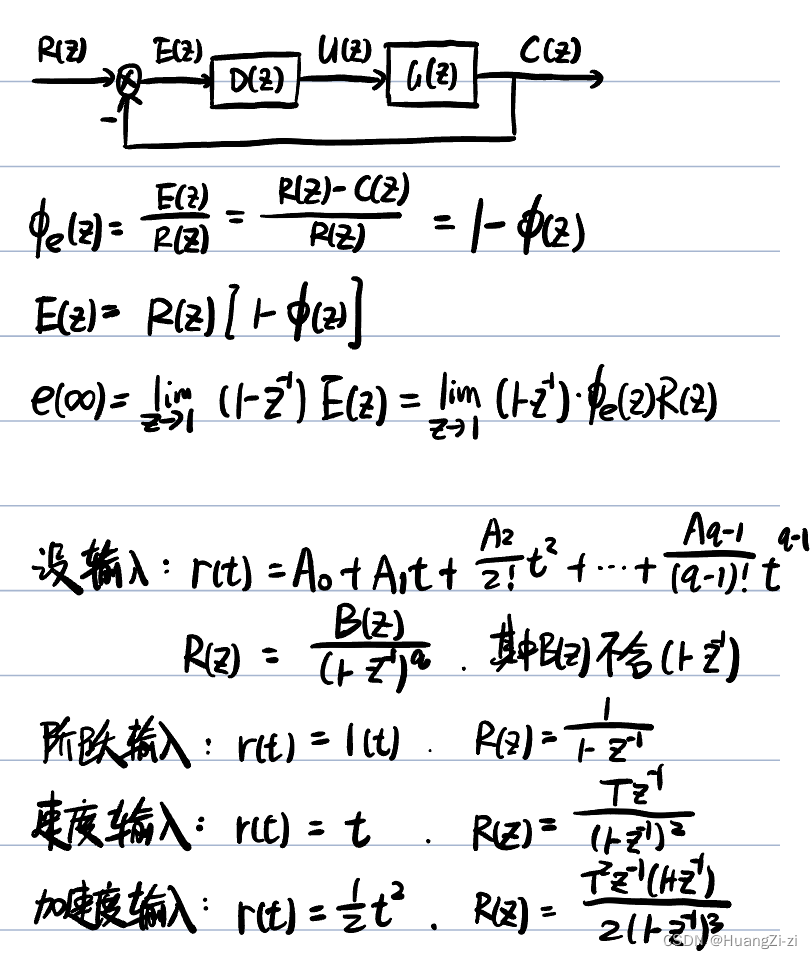

典型输入函数的最小拍无差系统
-
阶跃输入:
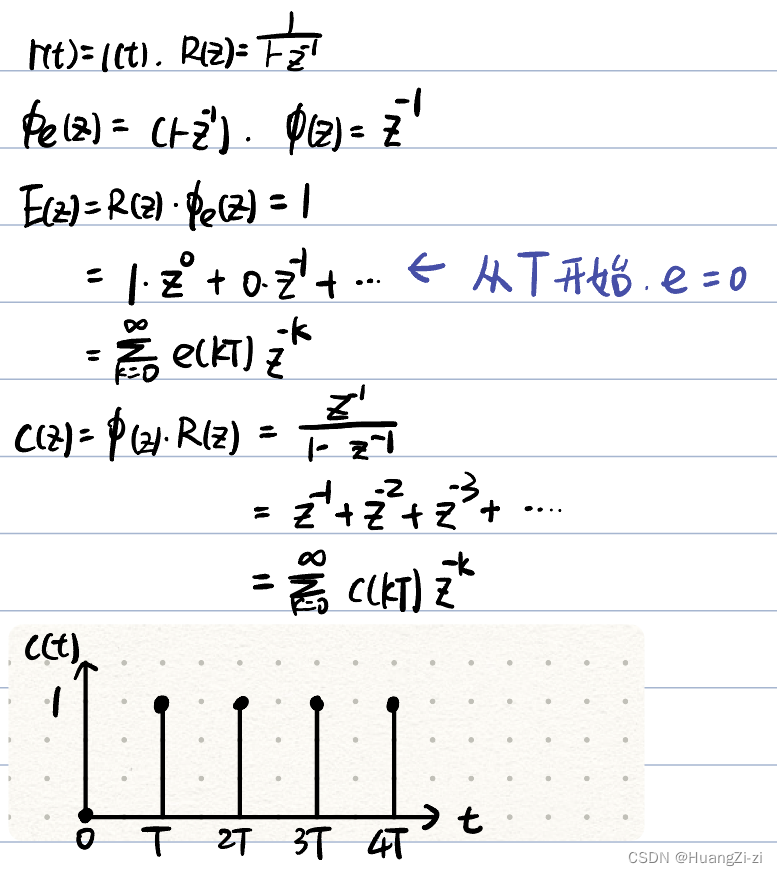
调节时间为T -
速度输入:
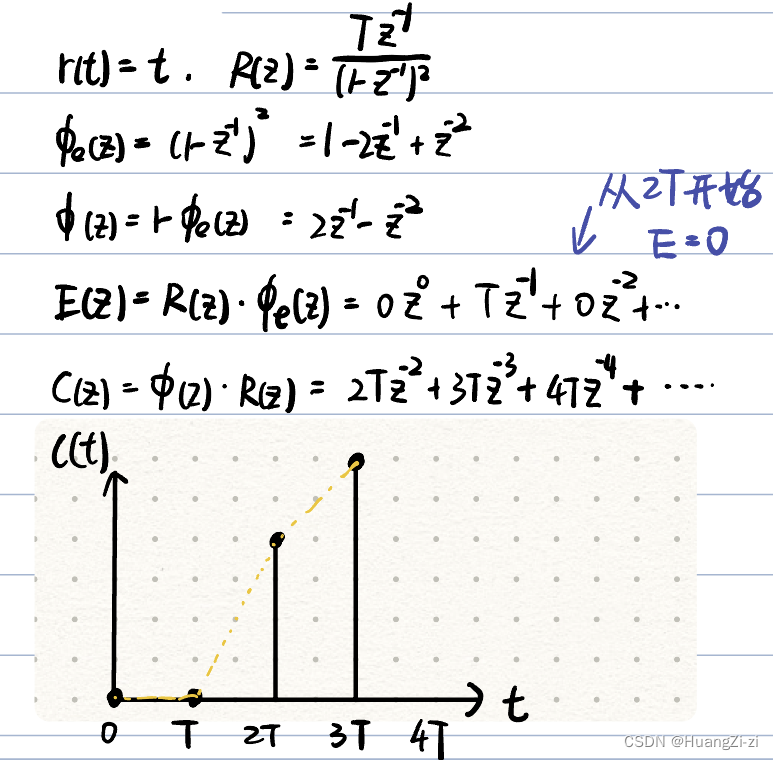
调节时间为2T -
加速度输入:
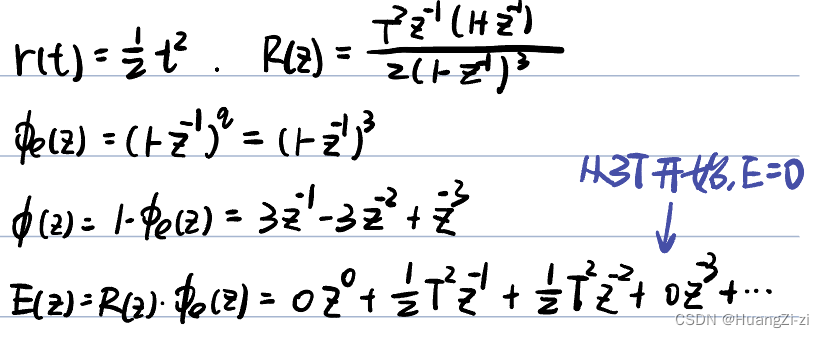
调节时间为3T
确定了 ϕ ( z ) \phi(z) ϕ(z)和 ϕ e ( z ) \phi_e(z) ϕe(z)以后,代入: D ( z ) = 1 G ( z ) ϕ ( z ) ϕ e ( z ) D(z)=\frac{1}{G(z)}\frac{\phi(z)}{\phi_e(z)} D(z)=G(z)1ϕe(z)ϕ(z)即可求出控制器的脉冲传函。
注意:针对一种典型输入函数设计的最小拍闭环脉冲传函 ϕ ( z ) \phi(z) ϕ(z)只适应这一种典型输入,不能适应各种输入。
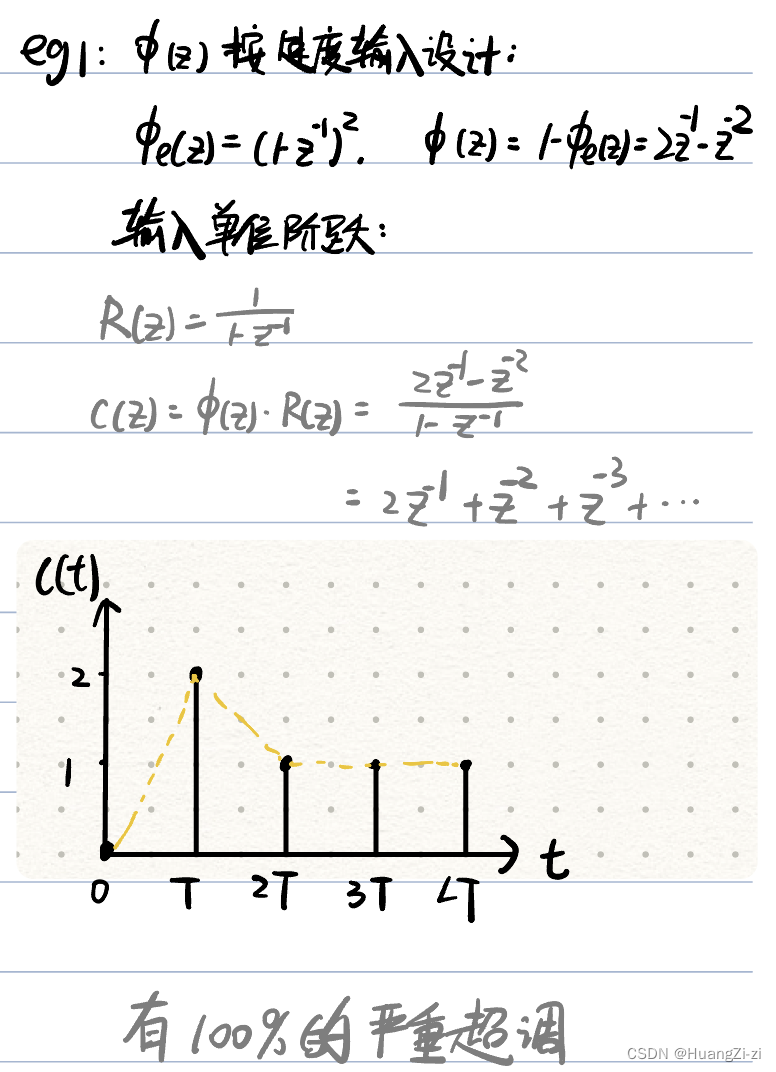
当输入次数较低的输入函数,会出现较大的超调、响应时间也增大,稳态误差为0
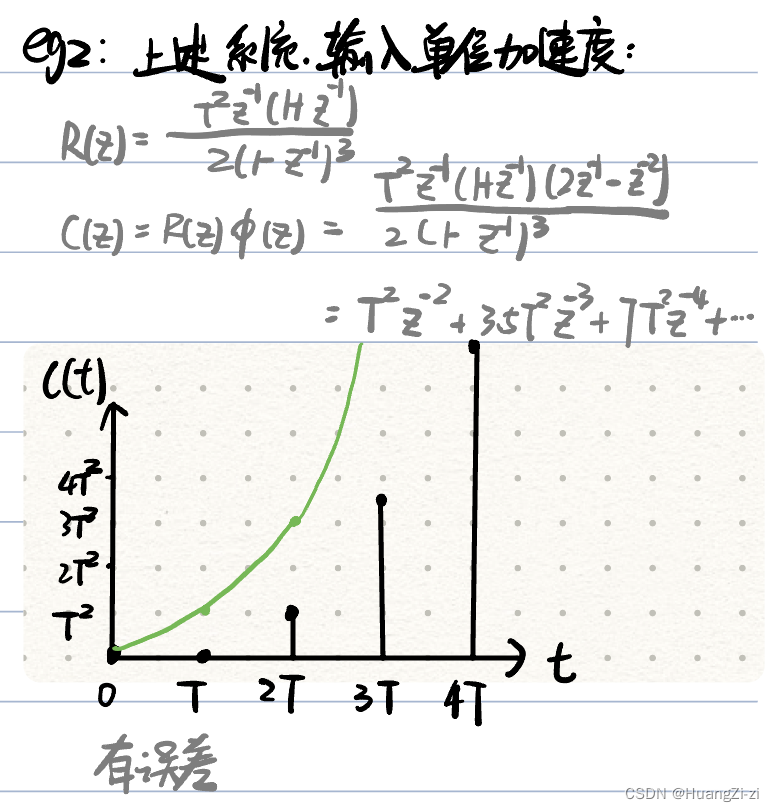
当输入次数较高的输入函数,输出不能完全跟踪输入,产生稳态误差
一般系统的最小拍无差设计
确定 ϕ ( z ) \phi(z) ϕ(z)的原则:



有波纹最小拍无差设计
也就是最一般的做法。遇到设计题没有特殊要求就这样做。


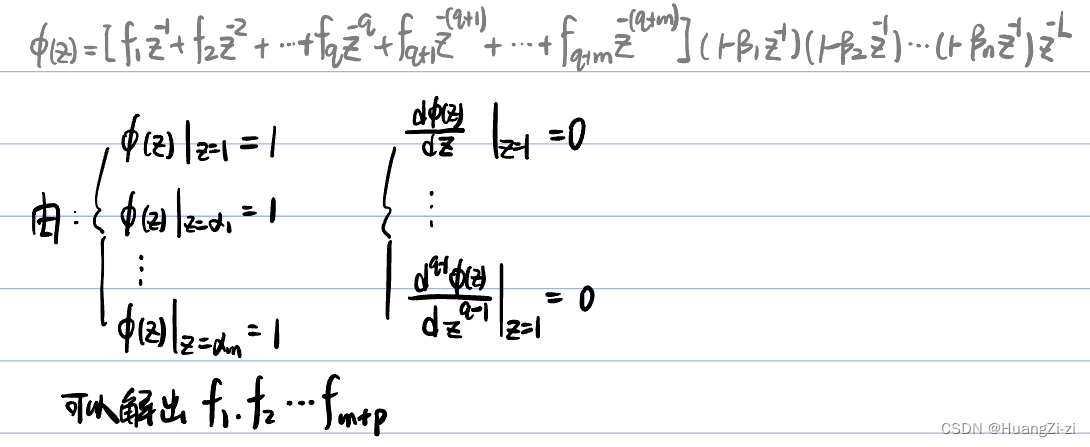
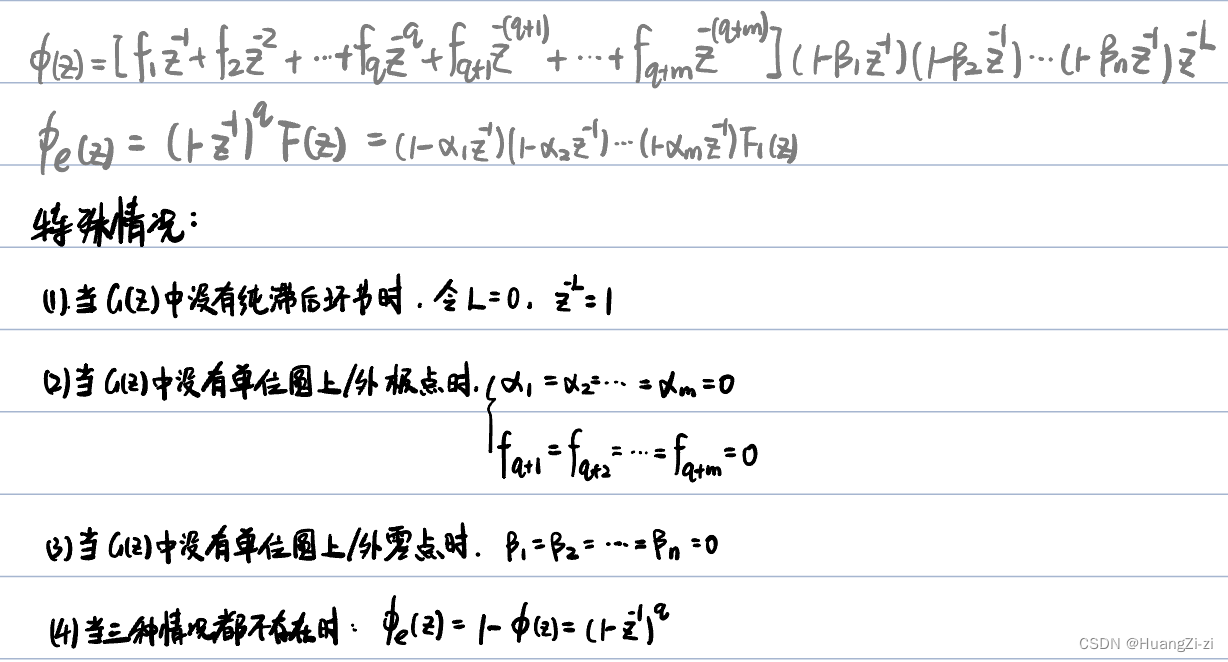
例题1:

例题2:

从这两道题可以看出:输出值可以跟随输入值。但控制器输出 u ( k ) u(k) u(k)不为常值,是震荡收敛的,因此在非采样时刻输出有误差,即有纹波(波纹)存在。
这样会浪费执行机构功率,增加机械磨损。
无波纹最小拍无差设计
需满足的条件:
- G ( z ) G(z) G(z)中有 q − 1 q-1 q−1个积分环节,q为输入型别
- 满足稳定性、物理可实现性
- ϕ ( z ) \phi(z) ϕ(z)中应包含 G ( z ) G(z) G(z)的所有零点
设计方法:

与有波纹的设计相比,区别在于:这次 ϕ ( z ) \phi(z) ϕ(z)包含了 G ( z ) G(z) G(z)的所有零点
例题3:


对比例题2和例题3,可以看出,无波纹设计,跟踪时间更长。
最小拍控制器的工程化改进
针对输入信号类型敏感问题
使用阻尼因子法。即在闭环脉冲传函中引入附加的阻尼因子,使输出偏差不立即为0,而是呈现一定的阻尼衰减特性,逐渐为0.
缺点是过渡时间增加
优点是输出对于不同信号的适应性有所改善

例题:


针对模型参数变化敏感问题
使用非最小的有限拍系统
把系统闭环脉冲传函的幂次提高1到2阶,使输出比最小拍多1到2拍才到达稳态。此时有更多可以设计的系数,即有更大的设计自由度,降低了模型参数变化的影响。


Dahlin算法
当要求系统没有超调或者超调很小时,不适用最小拍控制器。且实际工程中有很多纯滞后较大的系统,此时我们更加注意超调小或无超调,而允许调节时间为多个采样周期。
针对具有大滞后的一阶和二阶惯性环节,可以使用大林算法(Dahlin算法)
基本思路为:设计控制器,使得整个系统的闭环传函为带纯滞后的一阶环节。且闭环的纯滞后时间等于被控对象的纯滞后。
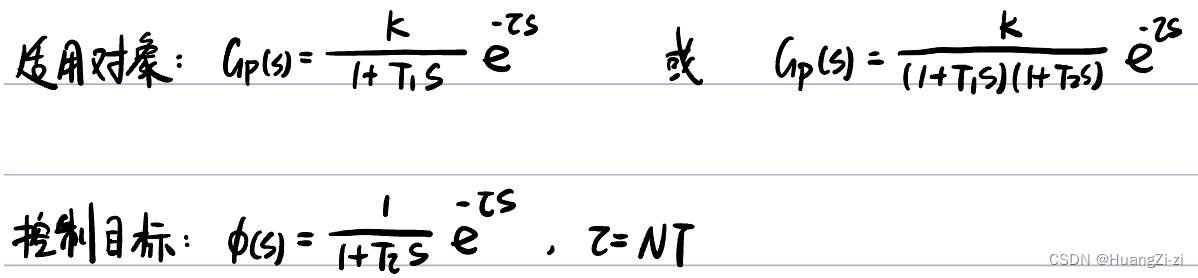
使用Dahlin算法设计控制器

根据被控对象是一阶还是二阶,方法比较固定,套公式就行:

例题1:

例题2:

振铃及其消除
在上面的例题2中可以看到,控制器的输出有大幅度的衰减震荡(意思是震荡幅度大,但振幅衰减),频率为1/2采样频率。这种现象叫做振铃。
- 振铃与波纹
- 振铃:由于被控对象中惯性环节的低通特性引起,对于输出没有影响,但增加了执行机构的磨损。
- 波纹:由于控制器输出震荡,引起输出一直有波动
-
振铃现象分析


T → 0 T\to0 T→0, z 2 = − C 2 C 1 → − 1 z_2=-\frac{C_2}{C_1}\to-1 z2=−C1C2→−1,易产生振铃,因此 T T T可以适当增大 -
振铃幅度RA

-
振铃的消除


-
工程中关键参数的选择
- 根据需要确定 T τ T_\tau Tτ和 R A RA RA的指标
- R A = C 2 C 1 − e − T T τ + e − T T 1 + e − T T 2 RA=\frac{C_2}{C_1}-e^{-\frac{T}{T_\tau}}+e^{-\frac{T}{T_1}}+e^{-\frac{T}{T_2}} RA=C1C2−e−TτT+e−T1T+e−T2T。通过上式计算T
- N = τ / T N=\tau /T N=τ/T,确定N
- 计算 G ( z ) G(z) G(z)和 ϕ ( z ) \phi(z) ϕ(z)
- 求 D ( z ) D(z) D(z)
相关文章:

「计算机控制系统」6. 直接设计法
特殊类型系统的最小拍无差设计 一般系统的最小拍无差设计 最小拍控制器的工程化改进 Dahlin算法 文章目录 特殊类型系统的最小拍无差设计理论分析典型输入函数的最小拍无差系统 一般系统的最小拍无差设计有波纹最小拍无差设计无波纹最小拍无差设计 最小拍控制器的工程化改进针对…...
什么是JWT?
起源 需要了解一门技术,首先从为什么产生开始说起是最好的。JWT 主要用于用户登录鉴权,所以我们从最传统的 session 认证开始说起。 session认证 众所周知,http 协议本身是无状态的协议,那就意味着当有用户向系统使用账户名称和…...

STM32—0.96寸OLED液晶显示
本文主要介绍基于STM32F103的0.96寸的OLED液晶显示,详细关于0.96寸OLED液晶屏幕的介绍可参考这篇博客:https://blog.csdn.net/u011816009/article/details/130119426 一、简介 OLED被称为有机激光二极管,也被称为有机激光显示,O…...

Mysql的简介和选择
文章目录 前言一、为什么要使用数据库 数据库的概念为什么要使用数据库二、程序员为什么要学习数据库三、数据库的选择 主流数据库简介使用MySQL的优势版本选择四、Windows 平台下安装与配置MySQL 启动MySQL 服务控制台登录MySQL命令五、Linux 平台下安装与配置MySQL总结 前言…...

3D视觉之深度相机方案
随着机器视觉,自动驾驶等颠覆性的技术逐步发展,采用 3D 相机进行物体识别,行为识别,场景 建模的相关应用越来越多,可以说 3D 相机就是终端和机器人的眼睛。 3D 相机 3D 相机又称之为深度相机,顾名思义&…...
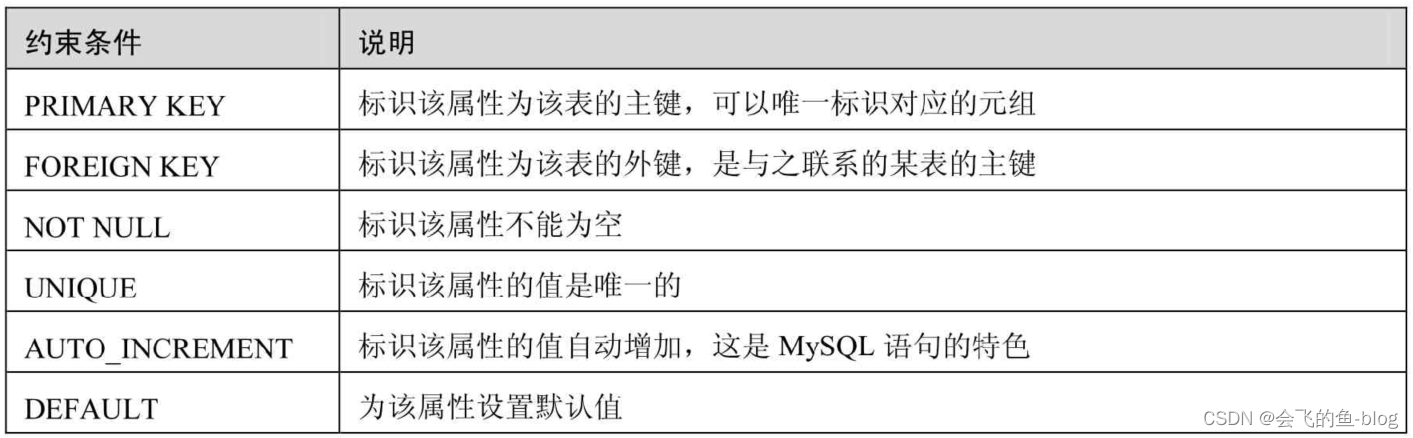
Mysql列的完整性约束详解(主键约束)
文章目录 前言一、设置表字段的主键约束(PRIMARY KEY,PK) 1.单字段主键2.多字段主键总结 前言 完整性约束条件是对字段进行限制,要求用户对该属性进行的操作符合特定的要求。如果不满足完整性约束条件,数据库系统将不再…...
母婴市场竞争激烈,如何通过软文营销脱颖而出
如今,随着宝宝数量增加以及人们对孩子的重视程度的增加,母婴市场愈发火爆。然而,母婴行业的竞争也越来越激烈,企业需要不断开拓新市场才能生存。在这样的情况下,软文营销成为了母婴企业拓展市场的一种有效方式。 首先&…...

java--线程池
目录 1.线程池概 2 为什么要使用线程池 1创建线程问题 2解决上面两个问题思路: 3线程池的好处 4线程池适合应用场景 3 线程池的构造函数参数 1.corePoolSize int 线程池核心线程大小 2.maximumPoolSize int 线程池最大线程数量 3.keepAliveTime long 空闲…...

asp.net765数码手机配件租赁系统
员工部分功能 1.员工登录,员工通过自己的账号和密码登录到系统中来,对租赁信息进行管理 2.配件查询,员工可以查询系统内的配件信息 3.客户信息管理,员工可以管理和店内有业务往来的客户信息 4.配件租赁,员工可以操作用…...

有关态势感知(SA)的卷积思考
卷积是一种数学运算,其本质是将两个函数进行操作,其中一个函数是被称为卷积核或滤波器的小型矩阵,它在另一个函数上滑动并产生新的输出。在计算机视觉中,卷积通常用于图像处理和特征提取,它可以通过滤波器对输入图像进…...
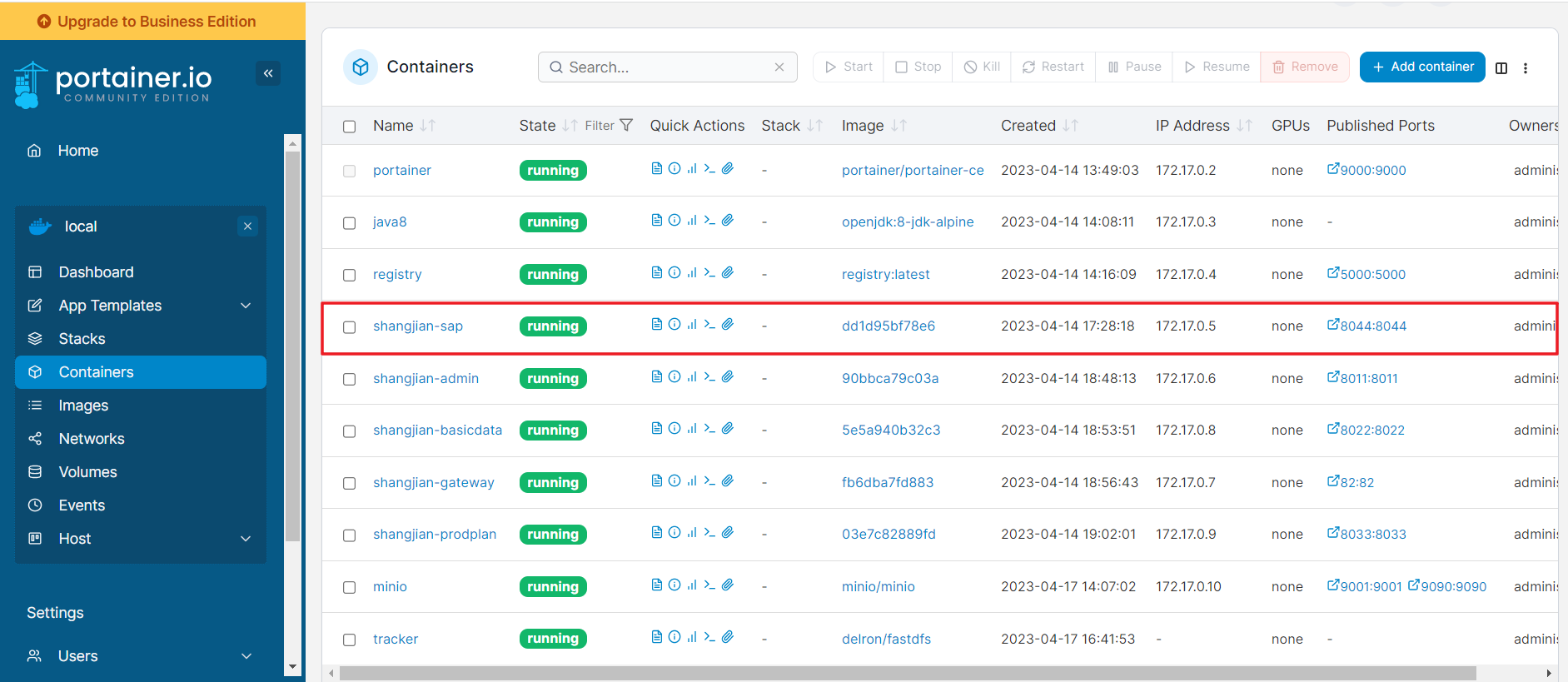
Docker快速部署springboot项目
有很多开发者在项目部署过程中都会遇到一些繁琐的问题,比如打包、上传、部署等。而使用Docker可以非常方便地解决这些问题。在本文中,将详细讲解如何使用IDEA中的docker打包插件,将代码打包并直接发布到服务器上。这样,我们就可以…...

Linux命令rsync增量同步目录下的文件
业务场景描述 最近遇到一个问题,需要编写相应的Linux命令,增量同步/var/mysql里的所有文件到另外一个目录/opt/mysql,但是里面相关的日志文件xx.log是不同步的,这个场景,可以使用rsync来实现 什么是rsync命令&#x…...
项目管理一般知识)
项目管理---(1)项目管理一般知识
一、项目管理一般知识 1.1 项目的一般知识 1.1.1 项目的定义: 项目是为创造独特的产品、服务或成果而进行的临时性工作。 1.1.2 项目的目标: 项目的目标包括成果性目标和约束性目标。 成果性目标:指通过项目开发出满足客户要求的产品、系…...

超过50多个热门的免费可用 API 分享
今天吃什么:随机返回一顿美味食物,解决你今天吃什么的难题。万年历:获取公历日期对应的农历、农历节日节气、天干地支纪年纪月纪日、生肖属相、宜忌、星座等信息。支持查询未来15天。笑话大全:各种最新、最及时的幽默、搞笑段子&a…...

记一次死锁问题
最近在做一个需求,碰到了死锁的问题,记录下解决问题的过程 背景 这个需求要改动一个接口,我这边称为A接口,原先的逻辑是A接口内部会调用c方法,c方法是一个dubbo方法, 现在需要再A接口里添加调用B方法&…...
Bean 作⽤域和⽣命周期
目录 1.lombok 1.1 1.添加依赖:(pom.xml) 1.2 在实体类上使用lombok提供的注解 1.3 安装插件 2. Bean 的 6 种作⽤域(Scope) 2.1 singleton(默认模式) 2.2 prototype(原型模式…...

SVN通过备份、过滤、再导入的方式彻底删除废弃目录
文章目录 前言简要步骤操作示例总结 前言 SVN占用的空间随着项目版本迭代越来越大,因为保存了历史记录中的各个版本,所以即使本地把废弃的目录删掉提交,也不会释放出多余的空间,大概率因为操作删除增加了一个版本号,使…...

golang支持优雅关闭和core错误记录
#经过测试,不能使用 ENTRYPOINT ["/modapi/modapi", "1>> /dev/null","2>> ./logs/stderr.log"],原因是虽然这种方案可以 #保证modapi命令为1号程序,能够接收到os的signal信号。但是如果程序core了…...

Basics of Container Isolation 容器隔离的实现原理
目录 容器隔离的实现原理 1. 使用cgroups实现资源隔离 自定义一个cgroup 设置进程的内存使用 启动一个docker 容器,观察cgroup的创建情况 2. 使用Namespaces进行资源分区 namespace继承关系引发的问题 3. 结合来使用Namespaces 和chroot 4. 结论 参考文档…...

EBS R12.1 注册客户化应用的步骤
创建客户化应用目录 登录成 applxxx 用户 -- applxxx 改成所需用户名 # 以标准INV模块作为客户化应用目录的模板 cd $APPL_TOP mkdir -p cust cp -r inv cust/template cd cust # 删除template 目录下的文件,只保留目录结构 cd $APPL_TOP/cust for rm_list in …...

谷歌浏览器插件
项目中有时候会用到插件 sync-cookie-extension1.0.0:开发环境同步测试 cookie 至 localhost,便于本地请求服务携带 cookie 参考地址:https://juejin.cn/post/7139354571712757767 里面有源码下载下来,加在到扩展即可使用FeHelp…...

大数据学习栈记——Neo4j的安装与使用
本文介绍图数据库Neofj的安装与使用,操作系统:Ubuntu24.04,Neofj版本:2025.04.0。 Apt安装 Neofj可以进行官网安装:Neo4j Deployment Center - Graph Database & Analytics 我这里安装是添加软件源的方法 最新版…...

(十)学生端搭建
本次旨在将之前的已完成的部分功能进行拼装到学生端,同时完善学生端的构建。本次工作主要包括: 1.学生端整体界面布局 2.模拟考场与部分个人画像流程的串联 3.整体学生端逻辑 一、学生端 在主界面可以选择自己的用户角色 选择学生则进入学生登录界面…...

前端导出带有合并单元格的列表
// 导出async function exportExcel(fileName "共识调整.xlsx") {// 所有数据const exportData await getAllMainData();// 表头内容let fitstTitleList [];const secondTitleList [];allColumns.value.forEach(column > {if (!column.children) {fitstTitleL…...

学校招生小程序源码介绍
基于ThinkPHPFastAdminUniApp开发的学校招生小程序源码,专为学校招生场景量身打造,功能实用且操作便捷。 从技术架构来看,ThinkPHP提供稳定可靠的后台服务,FastAdmin加速开发流程,UniApp则保障小程序在多端有良好的兼…...

剑指offer20_链表中环的入口节点
链表中环的入口节点 给定一个链表,若其中包含环,则输出环的入口节点。 若其中不包含环,则输出null。 数据范围 节点 val 值取值范围 [ 1 , 1000 ] [1,1000] [1,1000]。 节点 val 值各不相同。 链表长度 [ 0 , 500 ] [0,500] [0,500]。 …...
)
GitHub 趋势日报 (2025年06月08日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 884 cognee 566 dify 414 HumanSystemOptimization 414 omni-tools 321 note-gen …...

docker 部署发现spring.profiles.active 问题
报错: org.springframework.boot.context.config.InvalidConfigDataPropertyException: Property spring.profiles.active imported from location class path resource [application-test.yml] is invalid in a profile specific resource [origin: class path re…...

Unsafe Fileupload篇补充-木马的详细教程与木马分享(中国蚁剑方式)
在之前的皮卡丘靶场第九期Unsafe Fileupload篇中我们学习了木马的原理并且学了一个简单的木马文件 本期内容是为了更好的为大家解释木马(服务器方面的)的原理,连接,以及各种木马及连接工具的分享 文件木马:https://w…...

JAVA后端开发——多租户
数据隔离是多租户系统中的核心概念,确保一个租户(在这个系统中可能是一个公司或一个独立的客户)的数据对其他租户是不可见的。在 RuoYi 框架(您当前项目所使用的基础框架)中,这通常是通过在数据表中增加一个…...
