442. 数组中重复的数据|||41. 缺失的第一个正数|||485. 最大连续 1 的个数
442. 数组中重复的数据
题目
给你一个长度为 n 的整数数组 nums ,其中 nums 的所有整数都在范围 [1, n] 内,且每个整数出现 一次 或 两次 。请你找出所有出现 两次 的整数,并以数组形式返回。
你必须设计并实现一个时间复杂度为 O(n) 且仅使用常量额外空间的算法解决此问题。
代码
class Solution {public List<Integer> findDuplicates(int[] nums) {List<Integer> list=new ArrayList<>();int n=nums.length;for(int i=0;i<n;i++){nums[(nums[i]-1)%n]+=n;}for(int i=0;i<n;i++){if(nums[i]>2*n)list.add(i+1);}return list;}
}
思考
和之前做过的找数组中消失的数字,思路是类似的
直接用自身数组当成了辅助数组
41. 缺失的第一个正数
题目
给你一个未排序的整数数组 nums ,请你找出其中没有出现的最小的正整数。
请你实现时间复杂度为 O(n) 并且只使用常数级别额外空间的解决方案。
代码
## 排序了,时间复杂度不满足O(n)
class Solution {public int firstMissingPositive(int[] nums) {int ans=1;Arrays.sort(nums);for(int i=0;i<nums.length;i++){if(nums[i]>0 && nums[i]==ans)ans++;}return ans;}
}class Solution {public int firstMissingPositive(int[] nums) {int n=nums.length;for(int i=0;i<n;i++){if(nums[i]<=0)nums[i]=n+1;}for(int i=0;i<n;i++){int temp=Math.abs(nums[i]);if(temp-1<n)nums[temp-1]=-Math.abs(nums[temp-1]);}for(int i=0;i<n;i++){if(nums[i]>0)return i+1;}return n+1;}
}
思考
在空间复杂度有限制的情况下,那就是要原地哈希,或者自身当做自己辅助数组,但我就是没有想出来(╥╯^╰╥)。如果上一道题442. 数组中重复的数据我没有偷懒,用官解二,添负号的标记方法写了,也许能想出来吧,也许吧。
官解一思路:

有个小细节,不要重复添加。
485. 最大连续 1 的个数
题目
给定一个二进制数组 nums , 计算其中最大连续 1 的个数。
代码
class Solution {public int findMaxConsecutiveOnes(int[] nums) {int max=0,n=0;for(int i=0;i<nums.length;i++){if(nums[i]==0){max=n>max? n:max;n=0;} elsen++;}return max=n>max? n:max;}
}
思考
真正的简单题!
相关文章:

442. 数组中重复的数据|||41. 缺失的第一个正数|||485. 最大连续 1 的个数
442. 数组中重复的数据 题目 给你一个长度为 n 的整数数组 nums ,其中 nums 的所有整数都在范围 [1, n] 内,且每个整数出现 一次 或 两次 。请你找出所有出现 两次 的整数,并以数组形式返回。 你必须设计并实现一个时间复杂度为 O(n) 且仅…...
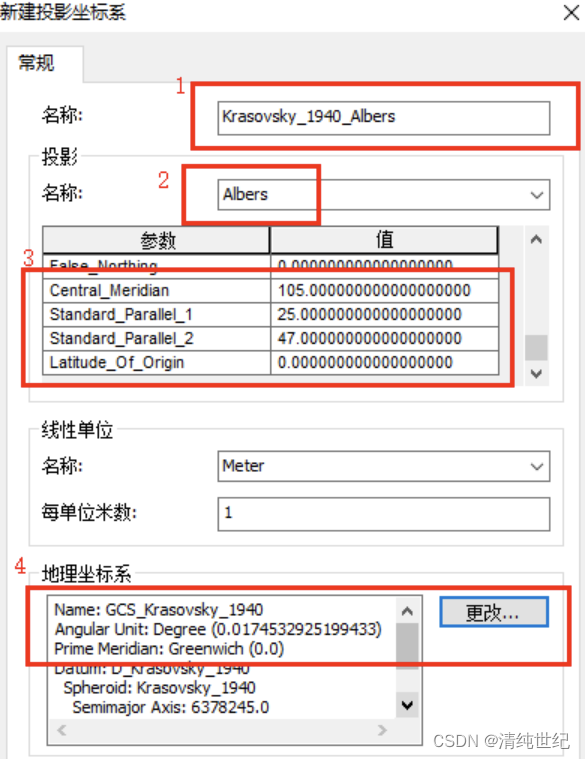
中国地图标准坐标和投影参数
目录 一、地理坐标 二、投影坐标 三、ArcGIS投影变换 四、说明 一、地理坐标 GCS_Krasovsky_1940(克拉索夫斯基_1940椭球体) 具体参数如下图: 每个国家或地区都有各自的基准面,我们通常所说的北京54坐标系、西安80坐标系实际上…...

CNN中卷积层、池化的计算公式
卷积计算公式 1、卷积层输入特征图(input feature map)的尺寸为:(batch_size,Channel,H,W) H(input)表示输入特征图的高 W(input)表示输入特征图的宽 C(input)表示输入特征图的通道数(如果是第一个卷积层则是输入图像的通道数,如果是中间…...

基类派生类多态虚函数?
通常在层次关系的根部有一个基类,其他类则直接或间接的从基类继承而来,这些继承得到的类称为派生类。基类负责定义在层次关系中所有类共同拥有的成员,而每个派生类定义各自特有的成员。 成员函数与继承派生类可以继承其基类的成员, 然而有时…...

像素是什么
像素分为设备像素和设备无关像素。 下面说说来龙去脉。 一、显示器 显示图像的电子设备。 (一)显示器种类 1.LCD LCD(Liquid crystal display),是液体晶体显示,也就是液晶显示器,LCD具有功耗低…...

NAT转换
目录标题 NAT:网络地址转换(cisco篇)一对一(静态)一对多(动态)多对多(动、静均可)端口映射(静态) nat:网络地址转换(华为篇࿰…...

设计模式:创建者模式 - 单例模式
文章目录 1.介绍2.单例模式的结构3.单例模式的实现(饿汉、懒汉)饿汉式-方式1(静态变量方式)饿汉式-方式2(静态代码块方式)懒汉式-方式1(线程不安全)懒汉式-方式2(线程安全…...

C++语言亚马逊国际获取AMAZON商品详情 API接口(
跨境电子商务是一种全新的互联网电商模式,运用电子化方式促成线上跨境交易,利用跨境物流运送商品,有利于打破传统的贸易格局,成为新的经济增长点。对我国来说,跨境电商平台正用一种全新的力量改变我国产业链的结构&…...
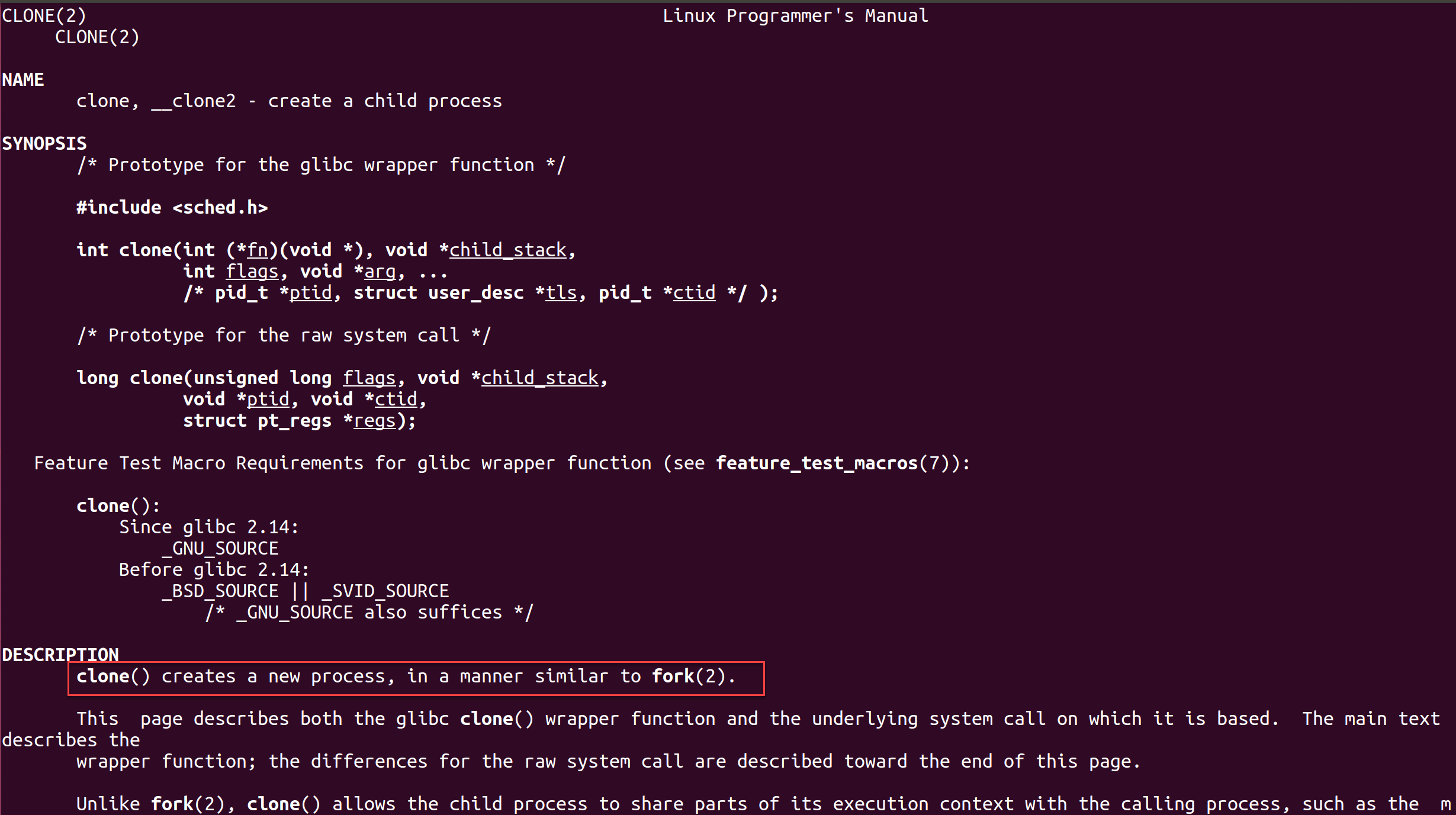
在程序里面执行system(“cd /某个目录“),为什么路径切换不成功?
粉丝提问: 彭老师,问下,在程序里面执行system(“cd /某个目录”),这样会切换不成功,为啥呢 实例代码: 粉丝的疑惑是明明第10行执行了cd /media操作, 为什么12行执行的pwd > test2.txt 结…...

c++ 对类与对象的基础框架+完整思维导图+基本练习题+深入细节+通俗易懂建议收藏
绪论 上一章,我们将c入门的基础知识进行了学习,本章其实才算真正的跨入到c开始可能比较难,但只有我们唯有不断的前进,才能斩断荆棘越过人生的坎坷! 话不多说安全带系好,发车啦(建议电脑观看&…...
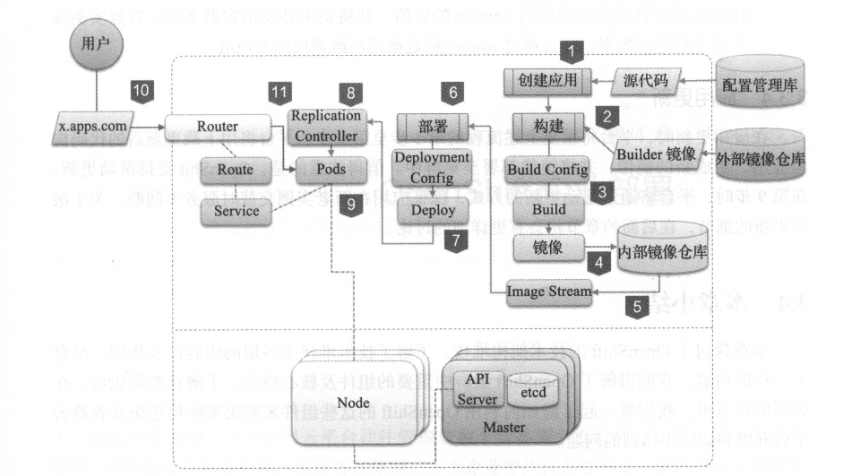
关于Open Shift(OKD) 中应用管理部署的一些笔记
写在前面 因为参加考试,会陆续分享一些 OpenShift 的笔记博文内容为介绍 openshift 不同的创建应用的方式,包括: 基于 IS 创建应用基于镜像创建应用基于源码和 image 创建应用基于源码和 IS 创建应用基于模板创建应用 学习环境为 openshift v…...
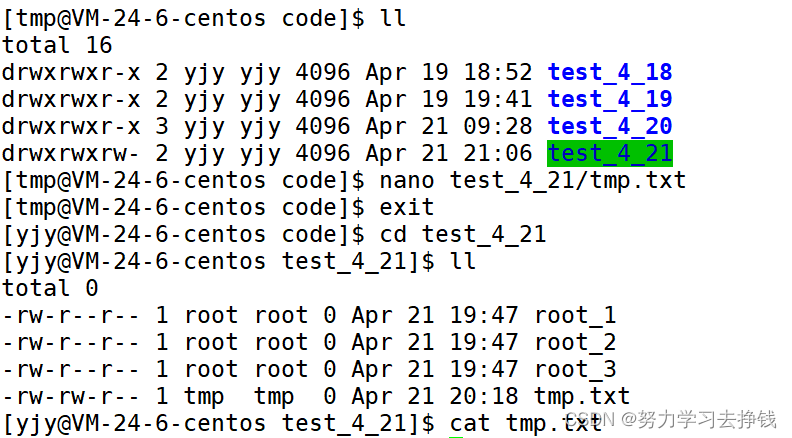
【linux】对于权限的理解
权限 Linux权限的概念用户之间的切换 Linux权限管理文件权限操作文件的人Linux文件默认权限的设置权限掩码 所属组/其他删除拥有者创建的文件文件拥有者、所属组的修改修改文件拥有者修改文件所属组一次性修改拥有者和所属组 目录的执行权限 Linux权限的概念 首先,…...
测试人必备技能:如何进行WebSocket接口测试?
目录 前言 WebSocket介绍 HTTP与WebSocket的区别 二者关系 WebSocket测试方法 使用Postman 使用Jmeter 使用Python 结语 前言 随着Web应用的日益普及,WebSocket作为一种全双工通信协议,在移动端、游戏、视频会议等方面得到广泛应用。 而对于需…...

【Android FrameWork (三)】- SystemServer
文章目录 知识回顾启动第一个流程initZygote的流程 前言源码分析1.system_server2.SystemServer.main3,startBootstrapServices4,startService 拓展知识LoadApkcontext 对于Android context 大家是怎么理解的?LocalServices.java: addServece方法中 ArrayMap和HashM…...

Docker容器部署及基本使用
文章目录 一、环境初始化配置二、安装Docker三、优化配置四、基础命令 一、环境初始化配置 1、关闭防火墙 systemctl stop firewalld systemctl disable firewalldsetenforce 0sed -i s/SELINUXenforcing/SELINUXdisabled/g /etc/selinux/config sed -i s/SELINUXenforcing/S…...
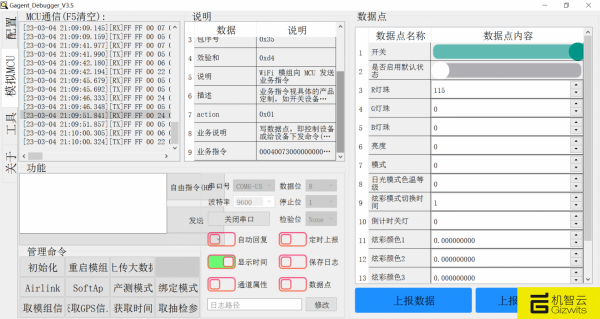
【机智云物联网低功耗转接板】+模拟MCU快速上手
GE211是机智云自研的定制化转接板,使用 ESP32-C3-WROOM-02 通讯模块,适用于白色智能家电等设备应用。 转接板已经烧录了机智云连云的最新GAgent固件,所以不需要烧写任何软件就可以快速上手使用。 GE211板卡带有一个串口,一般是把这…...

ai免费写作在线平台-ai免费伪原创文章生成器软件
ai伪原创能检测出来吗 人工智能技术可以检测伪原创,但是不是所有的伪原创都可以被检测出来。 现在有许多自然语言处理(NLP)算法和技术可以用来检测伪原创内容,例如文本相似度比较算法,语气分析算法等。这些算法可以检…...
Web自动化测试简介及web自动化测试实战交教程
一、认识web自动化测试 1.什么是自动化测试? 自动化测试的概念: 软件自动化测试就是通过测试工具或者其他手段,按照测试人员的预定计划对软件产品进行自动化测试,他是软件测试的一个重要组成部分,能够完成许多手工测试无法完成或…...

基于单片机的家庭应急电源设计
基于单片机的家庭应急电源 摘 要 本设计基于STC89C52单片机设计得应急电源,以应急电源为研究对象,单片机设计为控制集成IC,ADC为模数转换控制模块,无源蜂鸣器作为报警电路。系统分为单片机设计最小系统,AD转换控制模…...
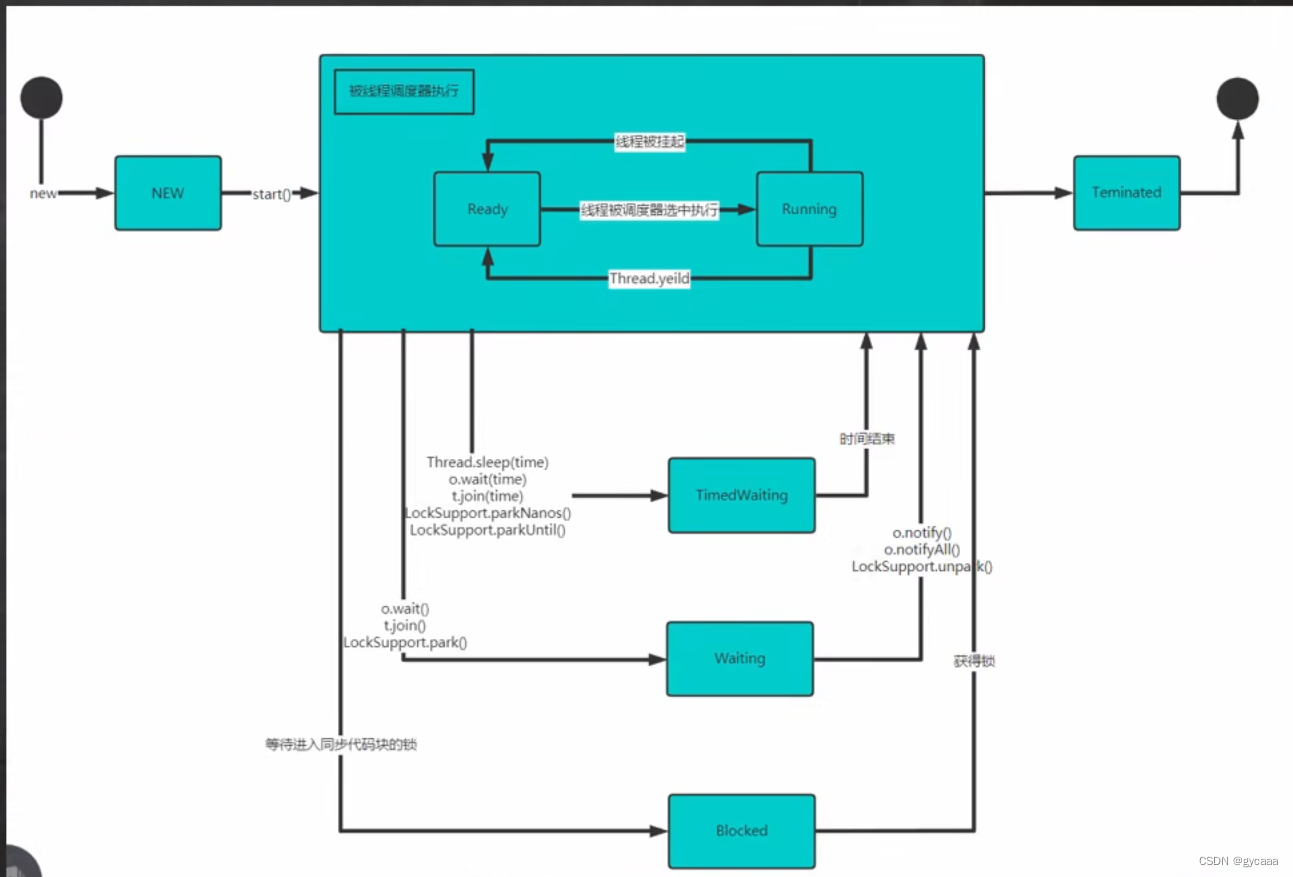
线程七大状态
线程生命周期(七大状态) 新建状态(New):当Java线程被创建时,它处于新建状态。此时,线程对象已被创建,但尚未启动。在这个状态下,线程并没有开始执行任何代码,…...

RocketMQ延迟消息机制
两种延迟消息 RocketMQ中提供了两种延迟消息机制 指定固定的延迟级别 通过在Message中设定一个MessageDelayLevel参数,对应18个预设的延迟级别指定时间点的延迟级别 通过在Message中设定一个DeliverTimeMS指定一个Long类型表示的具体时间点。到了时间点后…...

FFmpeg 低延迟同屏方案
引言 在实时互动需求激增的当下,无论是在线教育中的师生同屏演示、远程办公的屏幕共享协作,还是游戏直播的画面实时传输,低延迟同屏已成为保障用户体验的核心指标。FFmpeg 作为一款功能强大的多媒体框架,凭借其灵活的编解码、数据…...

微信小程序 - 手机震动
一、界面 <button type"primary" bindtap"shortVibrate">短震动</button> <button type"primary" bindtap"longVibrate">长震动</button> 二、js逻辑代码 注:文档 https://developers.weixin.qq…...

使用van-uploader 的UI组件,结合vue2如何实现图片上传组件的封装
以下是基于 vant-ui(适配 Vue2 版本 )实现截图中照片上传预览、删除功能,并封装成可复用组件的完整代码,包含样式和逻辑实现,可直接在 Vue2 项目中使用: 1. 封装的图片上传组件 ImageUploader.vue <te…...

EtherNet/IP转DeviceNet协议网关详解
一,设备主要功能 疆鸿智能JH-DVN-EIP本产品是自主研发的一款EtherNet/IP从站功能的通讯网关。该产品主要功能是连接DeviceNet总线和EtherNet/IP网络,本网关连接到EtherNet/IP总线中做为从站使用,连接到DeviceNet总线中做为从站使用。 在自动…...

让AI看见世界:MCP协议与服务器的工作原理
让AI看见世界:MCP协议与服务器的工作原理 MCP(Model Context Protocol)是一种创新的通信协议,旨在让大型语言模型能够安全、高效地与外部资源进行交互。在AI技术快速发展的今天,MCP正成为连接AI与现实世界的重要桥梁。…...

稳定币的深度剖析与展望
一、引言 在当今数字化浪潮席卷全球的时代,加密货币作为一种新兴的金融现象,正以前所未有的速度改变着我们对传统货币和金融体系的认知。然而,加密货币市场的高度波动性却成为了其广泛应用和普及的一大障碍。在这样的背景下,稳定…...

重启Eureka集群中的节点,对已经注册的服务有什么影响
先看答案,如果正确地操作,重启Eureka集群中的节点,对已经注册的服务影响非常小,甚至可以做到无感知。 但如果操作不当,可能会引发短暂的服务发现问题。 下面我们从Eureka的核心工作原理来详细分析这个问题。 Eureka的…...

使用Spring AI和MCP协议构建图片搜索服务
目录 使用Spring AI和MCP协议构建图片搜索服务 引言 技术栈概览 项目架构设计 架构图 服务端开发 1. 创建Spring Boot项目 2. 实现图片搜索工具 3. 配置传输模式 Stdio模式(本地调用) SSE模式(远程调用) 4. 注册工具提…...

mac 安装homebrew (nvm 及git)
mac 安装nvm 及git 万恶之源 mac 安装这些东西离不开Xcode。及homebrew 一、先说安装git步骤 通用: 方法一:使用 Homebrew 安装 Git(推荐) 步骤如下:打开终端(Terminal.app) 1.安装 Homebrew…...
