leetcode两数、三数、四数之和
如有错误,感谢不吝赐教、交流
文章目录
- 两数之和
- 题目
- 方法一:暴力两重循环(不可取)
- 方法二:HashMap空间换时间
- 三数之和
- 题目
- 方法一:当然是暴力破解啦
- 方法二:同两数之和的原理,借助HashMap和HashSet实现
- 四数之和
两数之和
题目
给定一个整数数组 nums 和一个整数目标值 target,请你在该数组中找出 和为目标值 target 的那 两个 整数,并返回它们的数组下标。
你可以假设每种输入只会对应一个答案。但是,数组中同一个元素在答案里不能重复出现。
你可以按任意顺序返回答案。
方法一:暴力两重循环(不可取)
方法二:HashMap空间换时间
借助HashMap实现,如下图示例

public int[] twoSum(int[] nums, int target) {HashMap<Integer, Integer> map = new HashMap<>();map.put(target - nums[0], 0);int res [] = new int[2];for (int i = 1; i < nums.length; i++) {Integer index = map.get(nums[i]);if (index != null) {res[0] = (int) index;res[1] = i;break;} else {map.put(target - nums[i], i);}}return res;}
三数之和
题目
给你一个整数数组 nums ,判断是否存在三元组 [nums[i], nums[j], nums[k]] 满足 i != j、i != k 且 j != k ,同时还满足 nums[i] + nums[j] + nums[k] == 0 。请
你返回所有和为 0 且不重复的三元组。
注意:答案中不可以包含重复的三元组。 这里尤其注意一下,不能包含重复的三元组(借助HashSet实现比较简单,不过有点费时间和空间)
方法一:当然是暴力破解啦
直接使用三重for循环暴力破解,太费时间,不可取。
方法二:同两数之和的原理,借助HashMap和HashSet实现
要求是三个数之和,这里将其中一个数保存到HashMap中,再使用双重for循环遍历,即可获得三个数的答案
原理是和两数之和的原理一样。
这里需要注意,会出现重复的组合结果,如[0, 0,0,0],可能得组合就有[0,0,0], [0,0,0], [0,0,0]
显然这里重复了,于是使用HashSet去重。
// 先对nums排序Arrays.sort(nums);HashMap<Integer, Integer> map = new HashMap<>();HashSet<List<Integer>> hashSet = new HashSet<>();map.put(-nums[0], 1);for (int i = 1; i < nums.length - 1; i++) {for (int j = i + 1; j < nums.length; j++) {int i1 = nums[i] + nums[j];Integer map_val = map.get(i1);if (map_val != null) {List<Integer> integers = new ArrayList<>();integers.add(-i1);integers.add(nums[i]);integers.add(nums[j]);hashSet.add(integers);}}map.put(-nums[i], 1);}List<List<Integer>> lists = new ArrayList<>(hashSet);return lists;
四数之和
方法原理和上面一样,借助HashMap和三重for循环实现
ps:计划每日更新一篇博客,今日2023-04-22,日更第六天,昨日更新:LeetCode6_N字形变换
相关文章:

leetcode两数、三数、四数之和
如有错误,感谢不吝赐教、交流 文章目录 两数之和题目方法一:暴力两重循环(不可取)方法二:HashMap空间换时间 三数之和题目方法一:当然是暴力破解啦方法二:同两数之和的原理,借助Has…...
使用Docker部署wikitten个人知识库
使用Docker部署wikitten个人知识库 一、wikitten介绍1.wikitten简介2.wikitten特点 二、本地实践环境介绍三、本地环境检查1.检查Docker服务状态2.检查Docker版本 四、部署wikitten个人知识库1.创建数据目录2.下载wikitten镜像3.创建wikitten容器4.查看wikitten容器状态5.检查w…...
【MYSQL】Java的JDBC编程(idea连接数据库)
1. 配置 (1)新建一个项目 (2)Build System 那里选择Maven,下一步Create (3)配置pom.xml文件 首先查看自己的MYSQL版本:进入MySQL命令窗口 我的MYSQL版本是8.0版本的. 下一步,…...
机器学习——主成分分析法(PCA)概念公式及应用python实现
机器学习——主成分分析法(PCA) 文章目录 机器学习——主成分分析法(PCA)一、主成分分析的概念二、主成分分析的步骤三、主成分分析PCA的简单实现四、手写体识别数字降维 一、主成分分析的概念 主成分分析(PCA&#x…...
手写axios源码系列二:创建axios函数对象
文章目录 一、模块化目录介绍二、创建 axios 函数对象1、创建 axios.js 文件2、创建 defaults.js 文件3、创建 _Axios.js 文件4、总结 当前篇章正式进入手写 axios 源码系列,我们要真枪实弹的开始写代码了。 因为 axios 源码的代码量比较庞大,所以我们这…...

HTB-Time
HTB-Time 信息收集80端口 立足pericles -> root 信息收集 80端口 有两个功能,一个是美化JSON数据。 一个是验证JSON,并且输入{“abc”:“abc”}之类的会出现报错。 Validation failed: Unhandled Java exception: com.fasterxml.jackson.core.JsonPa…...

零基础C/C++开发到底要学什么?
作者:黑马程序员 链接:https://www.zhihu.com/question/597037176/answer/2999707086 先和我一起看看,C/C学完了可以做什么: 软件工程师:负责设计、开发、测试和维护各类型的软件应用程序;游戏开发&#x…...

OpenStack中的CPU与内存超分详解
目录 什么是超分 CPU超分 查看虚拟机虚拟CPU运行在哪些物理CPU上 内存超分 内存预留 内存共享 如何设置内存预留和内存共享 全局设置 临时设置 什么是超分 超分通常指的是CPU或者GPU的分区或者分割,以在一个物理CPU或GPU内模拟多个逻辑CPU或GPU的功能。这…...

main.m文件解析--@autoreleasepool和UIApplicationMain
iOS 程序入口UIApplicationMain详解,相信大家新建一个工程的时候都会看到一个main.m文件,只不过我们很少了解它,现在我们分析一下它的作用是什么? 一、main.m文件 int main(int argc, char * argv[]) {autoreleasepool {return …...
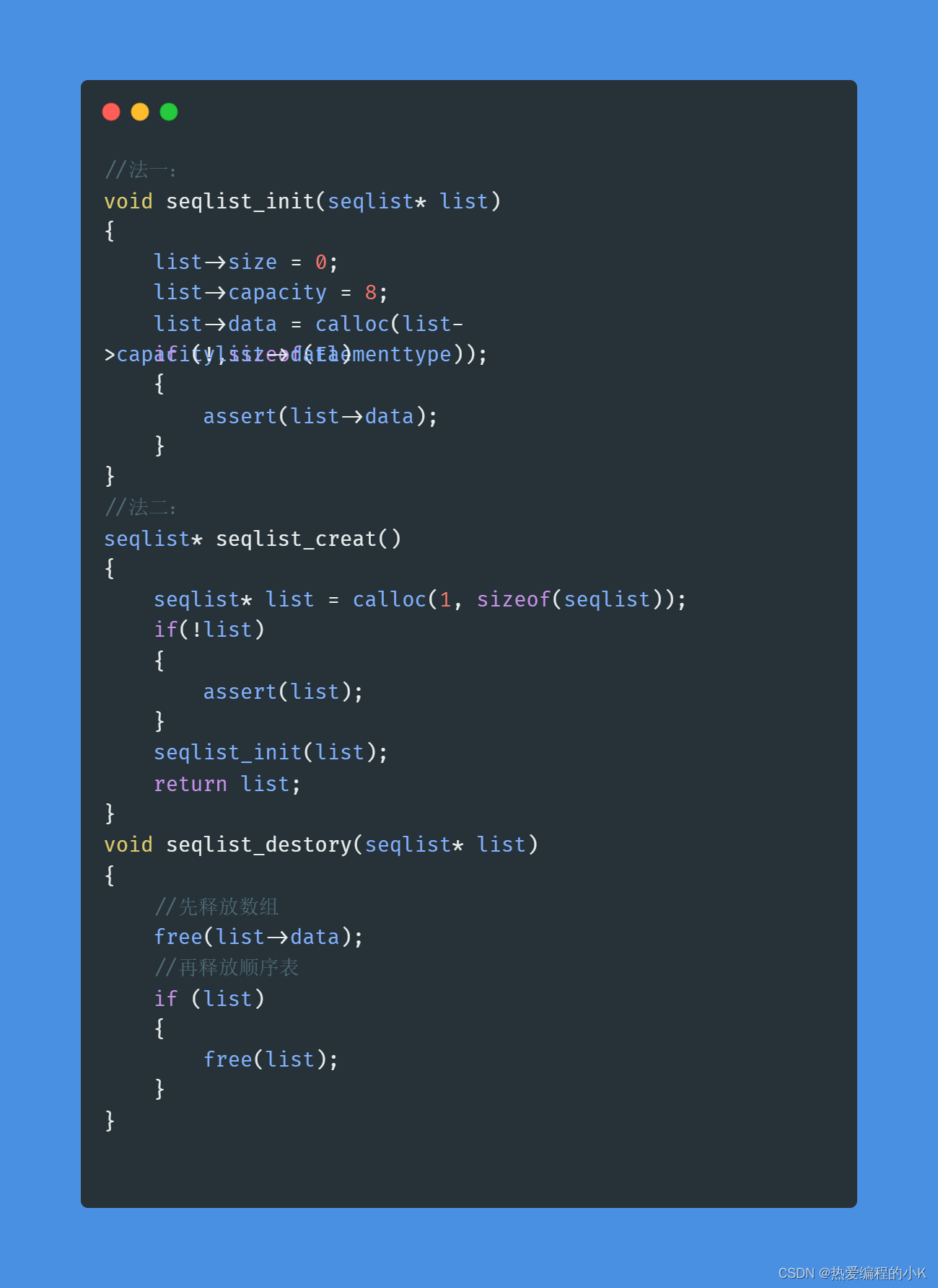
C语言复习之顺序表(十五)
📖作者介绍:22级树莓人(计算机专业),热爱编程<目前在c阶段>——目标C、Windows,MySQL,Qt,数据结构与算法,Linux,多线程,会持续分享…...
学系统集成项目管理工程师(中项)系列10_立项管理
1. 系统集成项目管理至关重要的一个环节 2. 重点在于是否要启动一个项目,并为其提供相应的预算支持 3. 项目建议 3.1. Request for Proposal, RFP 3.2. 立项申请 3.3. 项目建设单位向上级主管部门提交的项目申请文件,是对拟建项目提出的总体设想 3…...

电视盒子哪个好?数码小编盘点2023电视盒子排行榜
随着网络剧的热播,电视机又再度受宠,电视盒子也成为不可缺少的小家电。但面对复杂的参数和品牌型号,挑选时不知道电视盒子哪款最好,小编根据销量和用户评价整理半个月后盘点了电视盒子排行榜前五,对电视盒子哪个好感兴…...
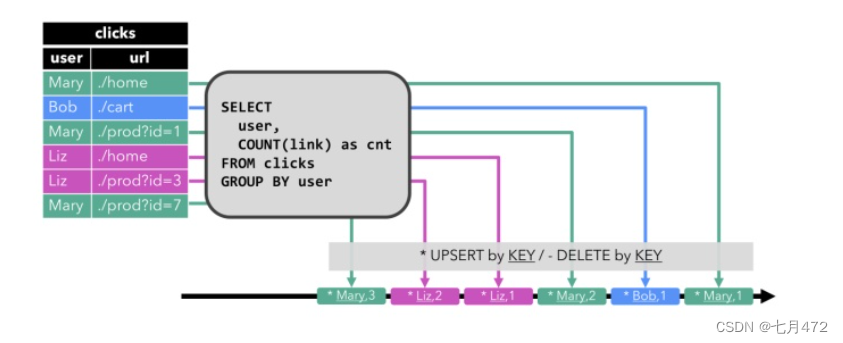
flink动态表的概念详解
目录 前言🚩 动态表和持续不断查询 stream转化成表 连续查询 查询限制 表转化为流 前言🚩 传统的数据库SQL和实时SQL处理的差别还是很大的,这里简单列出一些区别: 尽管存在这些差异,但使用关系查询和SQL处理流并…...

ArcGIS Pro用户界面
目录 1 功能区 1.1 快速访问工具栏 1.2 自定义快速访问工具栏 1.3 自定义功能区选项 1.3.1 添加组和命令 1.3.2 添加新选项卡 2 视图 3 用户界面排列 编辑 4 窗格 4.1 内容窗格 4.2 目录窗格 4.3 目录视图(类似ArcCatalog) 4.4 浏览对话框…...

HDCTF 2023 Pwn WriteUp
Index 前言Pwnner分析EXP: KEEP_ON分析EXP: Minions分析EXP: 后记: 前言 本人是菜狗,比赛的时候只做出来1题,2题有思路但是不会,还是太菜了。 栈迁移还是不会,但又都是栈迁移的题,真头大。得找时间好好学学…...

【 Spring 事务 】
文章目录 一、为什么需要事务(简单回顾)二、MySQL 中的事务使⽤三、Spring 中事务的实现3.1 Spring 编程式事务(手动事务)3.2 Spring 声明式事务(自动事务)3.2.1 Transactional 作⽤范围3.2.2 Transactional 参数说明3.2.3 Transactional 不进行事务回滚的情况3.2.4 Transactio…...
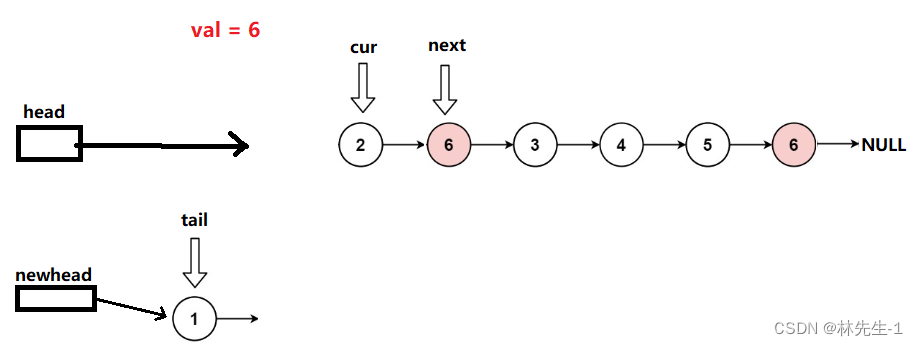
【刷题之路】LeetCode 203. 移除链表元素
【刷题之路】LeetCode 203. 移除链表元素 一、题目描述二、解题1、方法1——在原链表上动刀子1.1、思路分析1.2、代码实现 2、方法2——使用额外的链表2.1、思路分析2.2、代码实现 一、题目描述 原题连接: 203. 移除链表元素 题目描述: 给你一个链表的…...
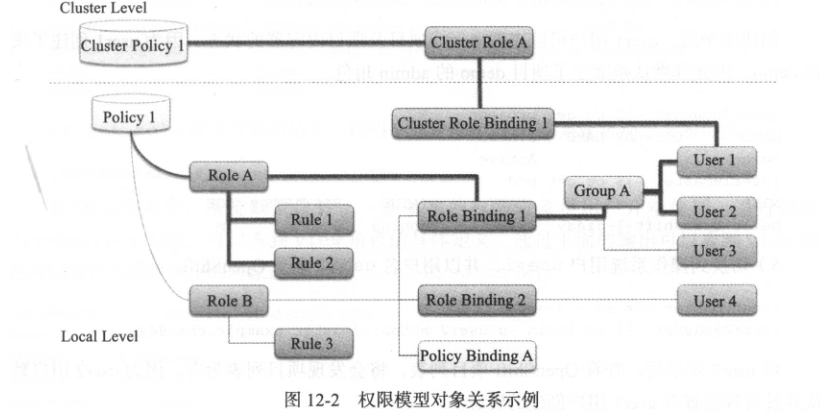
关于Open Shift(OKD) 中 用户认证、权限管理、SCC 管理的一些笔记
写在前面 因为参加考试,会陆续分享一些 OpenShift 的笔记博文内容为 openshift 用户认证和权限管理以及 scc 管理相关笔记学习环境为 openshift v3 的版本,有些旧这里如果专门学习 openshift ,建议学习 v4 版本理解不足小伙伴帮忙指正 对每个…...
)
活动文章测试(勿删)
大家好! 我是CSDN官方博客! 恭喜你正式加入CSDN博客,迈上技术成神之路~~ 路漫漫其修远兮——身为技术人,求索之路道阻且艰,但一万次的翘首却比不过一次的前行。 现在,就来开启你的个人博客,发布…...

Windows下 批量重命名文件【bat实现】
目录 前言 一、Windows简单实现重命名 二、使用命令行和Excel实现重命名 前言 在实际应用中,我们经常会遇到将指定文件夹下的文件重命名,以便程序读写。 本文介绍了两种方式,都是在Windows系统中自带的重命名方式。 一、Windows简单实现…...

在软件开发中正确使用MySQL日期时间类型的深度解析
在日常软件开发场景中,时间信息的存储是底层且核心的需求。从金融交易的精确记账时间、用户操作的行为日志,到供应链系统的物流节点时间戳,时间数据的准确性直接决定业务逻辑的可靠性。MySQL作为主流关系型数据库,其日期时间类型的…...

高危文件识别的常用算法:原理、应用与企业场景
高危文件识别的常用算法:原理、应用与企业场景 高危文件识别旨在检测可能导致安全威胁的文件,如包含恶意代码、敏感数据或欺诈内容的文档,在企业协同办公环境中(如Teams、Google Workspace)尤为重要。结合大模型技术&…...

【Web 进阶篇】优雅的接口设计:统一响应、全局异常处理与参数校验
系列回顾: 在上一篇中,我们成功地为应用集成了数据库,并使用 Spring Data JPA 实现了基本的 CRUD API。我们的应用现在能“记忆”数据了!但是,如果你仔细审视那些 API,会发现它们还很“粗糙”:有…...

BCS 2025|百度副总裁陈洋:智能体在安全领域的应用实践
6月5日,2025全球数字经济大会数字安全主论坛暨北京网络安全大会在国家会议中心隆重开幕。百度副总裁陈洋受邀出席,并作《智能体在安全领域的应用实践》主题演讲,分享了在智能体在安全领域的突破性实践。他指出,百度通过将安全能力…...

[Java恶补day16] 238.除自身以外数组的乘积
给你一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 不要使用除法,且在 O(n) 时间复杂度…...

AspectJ 在 Android 中的完整使用指南
一、环境配置(Gradle 7.0 适配) 1. 项目级 build.gradle // 注意:沪江插件已停更,推荐官方兼容方案 buildscript {dependencies {classpath org.aspectj:aspectjtools:1.9.9.1 // AspectJ 工具} } 2. 模块级 build.gradle plu…...

sipsak:SIP瑞士军刀!全参数详细教程!Kali Linux教程!
简介 sipsak 是一个面向会话初始协议 (SIP) 应用程序开发人员和管理员的小型命令行工具。它可以用于对 SIP 应用程序和设备进行一些简单的测试。 sipsak 是一款 SIP 压力和诊断实用程序。它通过 sip-uri 向服务器发送 SIP 请求,并检查收到的响应。它以以下模式之一…...

算法岗面试经验分享-大模型篇
文章目录 A 基础语言模型A.1 TransformerA.2 Bert B 大语言模型结构B.1 GPTB.2 LLamaB.3 ChatGLMB.4 Qwen C 大语言模型微调C.1 Fine-tuningC.2 Adapter-tuningC.3 Prefix-tuningC.4 P-tuningC.5 LoRA A 基础语言模型 A.1 Transformer (1)资源 论文&a…...
:观察者模式)
JS设计模式(4):观察者模式
JS设计模式(4):观察者模式 一、引入 在开发中,我们经常会遇到这样的场景:一个对象的状态变化需要自动通知其他对象,比如: 电商平台中,商品库存变化时需要通知所有订阅该商品的用户;新闻网站中࿰…...

[大语言模型]在个人电脑上部署ollama 并进行管理,最后配置AI程序开发助手.
ollama官网: 下载 https://ollama.com/ 安装 查看可以使用的模型 https://ollama.com/search 例如 https://ollama.com/library/deepseek-r1/tags # deepseek-r1:7bollama pull deepseek-r1:7b改token数量为409622 16384 ollama命令说明 ollama serve #:…...
