分治与减治算法实验: 排序中减治法的程序设计
目录
前言
实验内容
实验目的
实验分析
实验过程
流程演示
写出伪代码
实验代码
代码详解
运行结果
总结
前言
本文介绍了算法实验排序中减治法的程序设计。减治法是一种常用的算法设计技术,它通过减少问题的规模来求解问题。减治法可以应用于排序问题,例如插入排序、选择排序和快速排序等。本文将分析这些排序算法的原理、实现和性能,并给出相应的程序代码和测试结果。
本文中使用的语言是C语言,使用的工具是devc++
实验内容
给出一个记录序列,用堆排序的方法将其进行升序排列,输出结果,输出时要求有文字说明。请任选一种语言编写程序实现上述算法,并分析其算法复杂度。
实验目的
(1)掌握堆的有关概念;
(2)掌握堆排序的基本思想和其算法的实现过程;
(3)熟练掌握筛选算法的实现过程;
(4)在掌握的基础上编程实现堆排序的具体实现过程。
实验分析
这个题目要求使用堆排序的方法将一个记录序列进行升序排列,并输出结果和文字说明。需要选择一种编程语言来实现堆排序算法,并分析其算法复杂度。这个题目考察了对堆排序算法的理解和应用能力,以及你对编程语言的掌握程度和代码风格的规范性。需要注意以下几点:
- 堆排序算法是一种基于二叉堆结构的排序方法,它利用了二叉堆的性质,即堆顶元素是最大或最小值,来不断地选出序列中的最大或最小值,并将其放在正确的位置。它分为两个步骤:构建堆和调整堆。构建堆是从最后一个非叶子节点开始,自下而上地调整每个节点,使其满足大顶堆或小顶堆的性质。调整堆是从最后一个元素开始,将堆顶元素与末尾元素交换,然后调整剩余的元素为新的堆,重复这个过程直到只剩一个元素。
- 堆排序算法的时间复杂度为O(nlogn),空间复杂度为O(1)。它是一种原地排序算法,不需要额外的空间来存储数据。它的时间复杂度是由构建堆和调整堆的次数决定的,每次构建或调整堆都需要O(logn)的时间,而总共需要进行n次构建或调整,所以总的时间复杂度为O(nlogn)。它的空间复杂度是由交换元素所需的辅助空间决定的,每次交换只需要一个临时变量来存储数据,所以总的空间复杂度为O(1)。
实验过程
流程演示
- 首先,我们从最后一个非叶子节点开始,自下而上构建大顶堆。最后一个非叶子节点的索引是(n/2-1),其中n是序列的长度。在这个例子中,n=9,所以最后一个非叶子节点的索引是3,对应的元素是6。我们从这个节点开始,依次向上调整每个节点,使其满足大顶堆的性质。调整的过程是:比较当前节点和它的左右孩子,如果当前节点小于它的左右孩子中的任何一个,就交换它们,并递归地调整被交换的子树。调整后的结果如下:
9/ \8 7/ \ / \6 5 4 3/ \2 1
- 然后,我们将堆顶元素与末尾元素交换,即将9和1交换,这样我们就得到了序列中的最大值,并将其放在了正确的位置。交换后,我们将剩余的元素(除了最后一个)看作一个新的堆,并对其进行调整,使其满足大顶堆的性质。调整后的结果如下:
8/ \6 7/ \ / \2 5 4 3/
1
- 接着,我们重复上面的步骤,将堆顶元素与末尾元素交换,即将8和2交换,这样我们就得到了序列中的第二大值,并将其放在了正确的位置。交换后,我们将剩余的元素(除了最后两个)看作一个新的堆,并对其进行调整,使其满足大顶堆的性质。调整后的结果如下:
7/ \6 4/ \ /1 5 3/
2
- 我们继续重复上面的步骤,直到只剩一个元素为止。每次交换和调整后,我们都会得到序列中的一个最大值,并将其放在了正确的位置。最终,我们得到了升序排列的序列[1, 2, 3, 4, 5, 6, 7, 8, 9]
写出伪代码
//定义一个交换函数,接受一个数组和两个索引作为参数,交换这两个索引对应的元素
swap(arr, i, j):temp <- arr[i]arr[i] <- arr[j]arr[j] <- temp//定义一个调整函数,接受一个数组,一个数组的长度,和一个需要调整的节点的索引作为参数,调整该节点和它的子树,使其满足大顶堆的性质
heapify(arr, n, i):largest <- i //假设当前节点为最大值left <- 2 * i + 1 //左孩子的索引right <- 2 * i + 2 //右孩子的索引//如果左孩子存在且大于当前节点,更新最大值的索引if left < n and arr[left] > arr[largest]:largest <- left//如果右孩子存在且大于当前节点,更新最大值的索引if right < n and arr[right] > arr[largest]:largest <- right//如果最大值不是当前节点,交换它们,并递归地调整被交换的子树if largest != i:swap(arr, i, largest)heapify(arr, n, largest)//定义一个堆排序函数,接受一个数组和一个数组的长度作为参数,对该数组进行升序排列
heapSort(arr, n)://从最后一个非叶子节点开始,自下而上地构建大顶堆for i from n / 2 - 1 to 0:heapify(arr, n, i)//从最后一个元素开始,将堆顶元素与末尾元素交换,然后调整剩余的元素为新的大顶堆,重复这个过程直到只剩一个元素for i from n - 1 to 1:swap(arr, 0, i)heapify(arr, i, 0)//定义一个打印函数,接受一个数组和一个数组的长度作为参数,打印该数组中的每个元素
printArray(arr, n):for i from 0 to n - 1:print arr[i] and a spaceprint a newline//测试代码
main()://通过键盘输入序列的长度和元素print "请输入序列的长度:"read n //读取序列的长度print "请输入序列的元素:"arr <- an array of size n //动态分配内存空间存储序列for i from 0 to n - 1:read arr[i] //读取每个元素//输出原始序列print "原始序列:"printArray(arr, n)//使用堆排序算法对序列进行升序排列heapSort(arr, n)//输出排序结果print "排序结果:"printArray(arr, n)实验代码
#include <stdio.h>
#include <stdlib.h>//交换数组中的两个元素
void swap(int arr[], int i, int j) {int temp = arr[i];arr[i] = arr[j];arr[j] = temp;
}//调整数组中的元素,使其满足大顶堆的性质
void heapify(int arr[], int n, int i) {int largest = i; //假设当前节点为最大值int left = 2 * i + 1; //左孩子的索引int right = 2 * i + 2; //右孩子的索引//如果左孩子存在且大于当前节点,更新最大值的索引if (left < n && arr[left] > arr[largest]) {largest = left;}//如果右孩子存在且大于当前节点,更新最大值的索引if (right < n && arr[right] > arr[largest]) {largest = right;}//如果最大值不是当前节点,交换它们,并递归调整被交换的子树if (largest != i) {swap(arr, i, largest);heapify(arr, n, largest);}
}//堆排序算法
void heapSort(int arr[], int n) {//从最后一个非叶子节点开始,自下而上构建大顶堆for (int i = n / 2 - 1; i >= 0; i--) {heapify(arr, n, i);}//从最后一个元素开始,将堆顶元素与末尾元素交换,然后调整剩余的元素为新的大顶堆,重复这个过程直到只剩一个元素for (int i = n - 1; i > 0; i--) {swap(arr, 0, i);heapify(arr, i, 0);}
}//打印数组
void printArray(int arr[], int n) {for (int i = 0; i < n; i++) {printf("%d ", arr[i]);}printf("\n");
}//测试代码
int main() {//通过键盘输入序列的长度和元素printf("请输入序列的长度:\n");int n;scanf("%d", &n); //读取序列的长度printf("请输入序列的元素:\n");int *arr = (int *)malloc(sizeof(int) * n); //动态分配内存空间存储序列for (int i = 0; i < n; i++) {scanf("%d", &arr[i]); //读取每个元素}//输出原始序列printf("原始序列:\n");printArray(arr, n);//使用堆排序算法对序列进行升序排列heapSort(arr, n);//输出排序结果printf("排序结果:\n");printArray(arr, n);//释放内存空间free(arr);return 0;
}代码详解
代码分为以下几个部分:
- 交换数组中的两个元素的函数swap,它接受一个数组和两个索引作为参数,然后将这两个索引对应的元素互换位置。
- 调整数组中的元素,使其满足大顶堆的性质的函数heapify,它接受一个数组,一个数组的长度,和一个需要调整的节点的索引作为参数。它首先假设当前节点为最大值,然后比较它和它的左右孩子,如果左右孩子中有比它大的,就更新最大值的索引。如果最大值不是当前节点,就交换它们,并递归地调整被交换的子树。
- 堆排序算法的函数heapSort,它接受一个数组和一个数组的长度作为参数。它首先从最后一个非叶子节点开始,自下而上构建大顶堆。然后从最后一个元素开始,将堆顶元素与末尾元素交换,然后调整剩余的元素为新的大顶堆,重复这个过程直到只剩一个元素。
- 打印数组的函数printArray,它接受一个数组和一个数组的长度作为参数。它遍历数组中的每个元素,并打印出来。
- 测试代码的主函数main,它定义了一个待排序的序列,并调用了heapSort函数对其进行排序,并打印了排序前后的结果。
运行结果
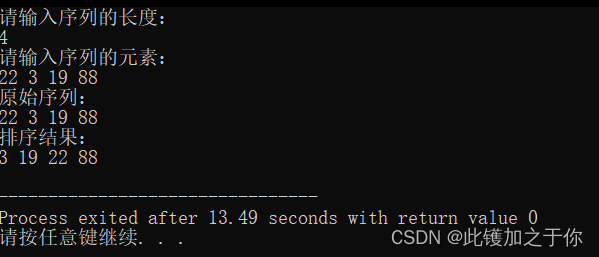
总结
减治法是一种算法设计策略,它的基本思想是将一个规模为n的问题转化为一个规模为n-1的子问题,然后利用子问题的解来求解原问题。减治法可以分为三种类型,分别是减去一个常量、减去一个常数因子和减去一个可变因子。在排序问题中,减治法有很多应用,例如插入排序、堆排序等。
插入排序是一种基于减一法的排序算法,它的过程类似于扑克牌抓牌时的排序。每次从未排序的序列中取出一个元素,将其插入到已排序的序列中合适的位置,使得已排序的序列仍然有序。插入排序的时间复杂度为O(n^2),空间复杂度为O(1)。插入排序是一种稳定的排序算法,也就是说,相同元素的相对顺序不会改变。
堆排序是一种基于减去常数因子的排序算法,它的过程利用了堆这种数据结构。堆是一种特殊的完全二叉树,它满足堆序性质,即每个节点的值都不小于(或不大于)其子节点的值。堆可以分为最大堆和最小堆,分别用于降序和升序排列。堆排序的过程分为两个步骤:建堆和调整堆。建堆是将一个无序的数组构造成一个堆,调整堆是每次将堆顶元素与最后一个元素交换,并将剩余的元素重新调整成一个堆,直到只剩下一个元素。堆排序的时间复杂度为O(nlogn),空间复杂度为O(1)。堆排序是一种不稳定的排序算法,也就是说,相同元素的相对顺序可能会改变。
相关文章:

分治与减治算法实验: 排序中减治法的程序设计
目录 前言 实验内容 实验目的 实验分析 实验过程 流程演示 写出伪代码 实验代码 代码详解 运行结果 总结 前言 本文介绍了算法实验排序中减治法的程序设计。减治法是一种常用的算法设计技术,它通过减少问题的规模来求解问题。减治法可以应用于排序问题&…...

leetcode两数、三数、四数之和
如有错误,感谢不吝赐教、交流 文章目录 两数之和题目方法一:暴力两重循环(不可取)方法二:HashMap空间换时间 三数之和题目方法一:当然是暴力破解啦方法二:同两数之和的原理,借助Has…...
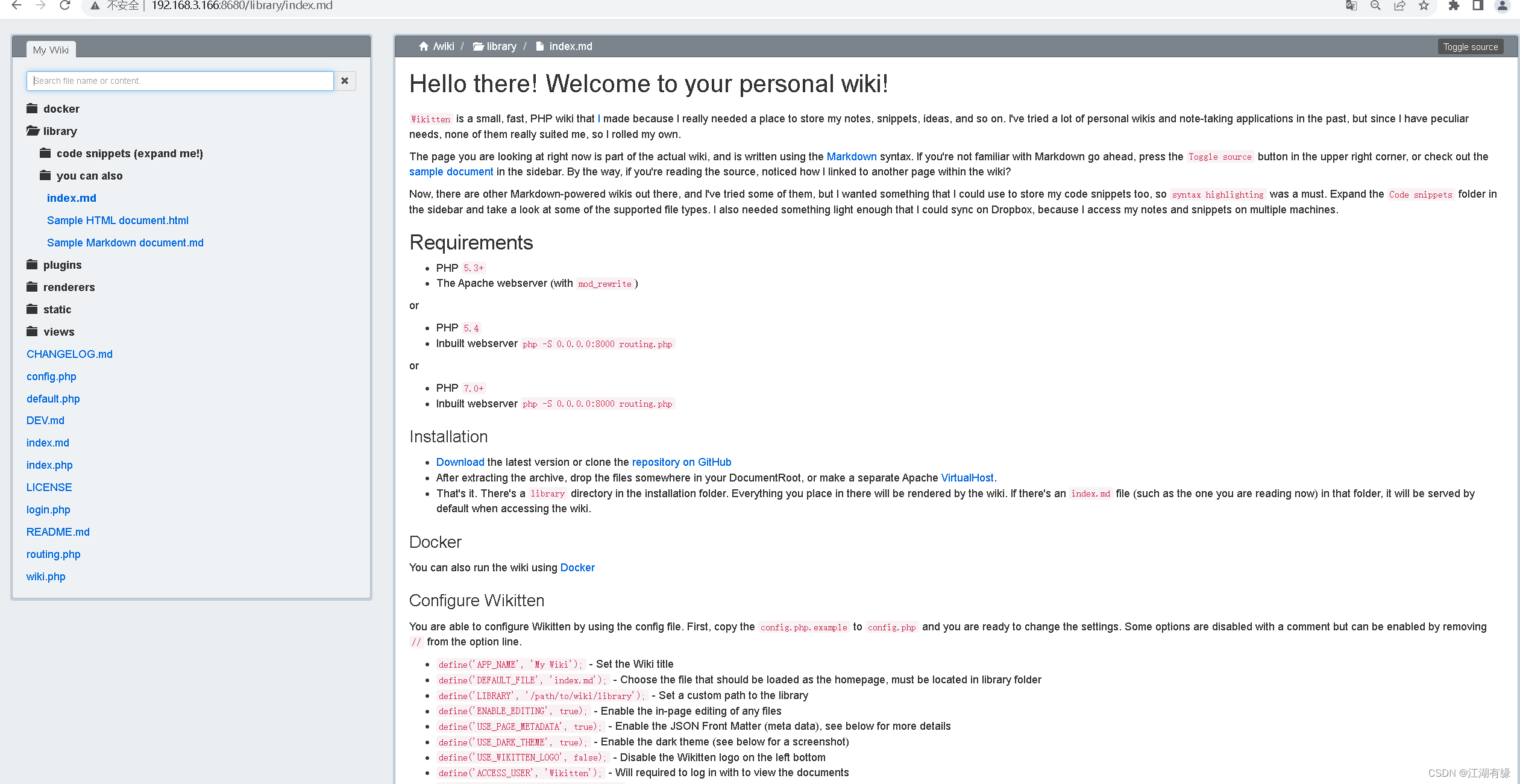
使用Docker部署wikitten个人知识库
使用Docker部署wikitten个人知识库 一、wikitten介绍1.wikitten简介2.wikitten特点 二、本地实践环境介绍三、本地环境检查1.检查Docker服务状态2.检查Docker版本 四、部署wikitten个人知识库1.创建数据目录2.下载wikitten镜像3.创建wikitten容器4.查看wikitten容器状态5.检查w…...
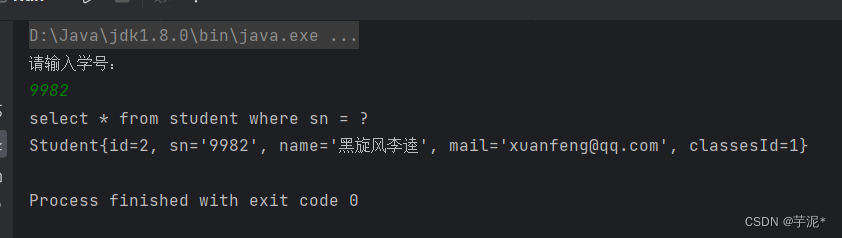
【MYSQL】Java的JDBC编程(idea连接数据库)
1. 配置 (1)新建一个项目 (2)Build System 那里选择Maven,下一步Create (3)配置pom.xml文件 首先查看自己的MYSQL版本:进入MySQL命令窗口 我的MYSQL版本是8.0版本的. 下一步,…...
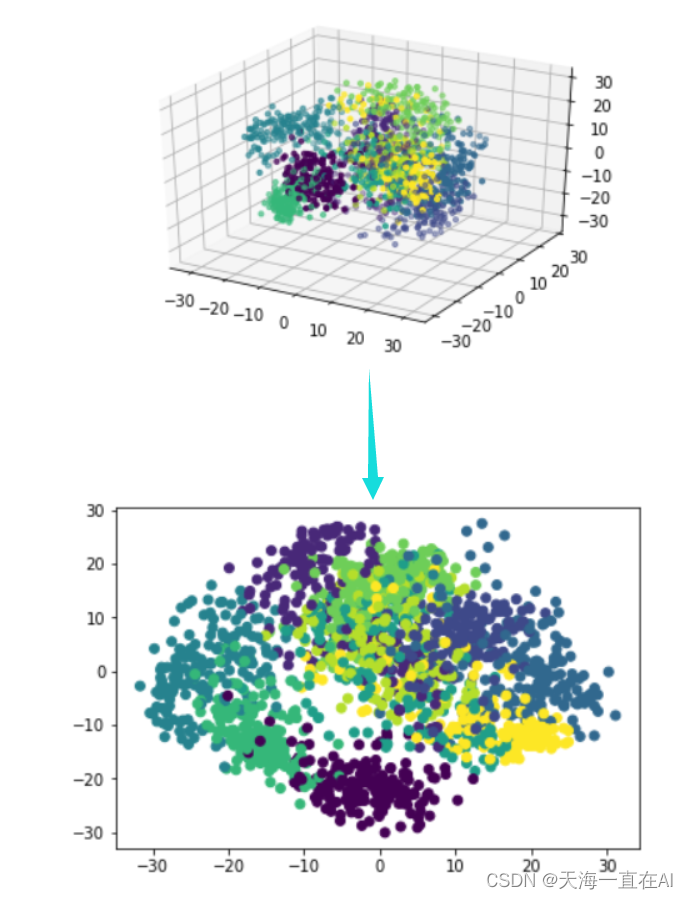
机器学习——主成分分析法(PCA)概念公式及应用python实现
机器学习——主成分分析法(PCA) 文章目录 机器学习——主成分分析法(PCA)一、主成分分析的概念二、主成分分析的步骤三、主成分分析PCA的简单实现四、手写体识别数字降维 一、主成分分析的概念 主成分分析(PCA&#x…...
手写axios源码系列二:创建axios函数对象
文章目录 一、模块化目录介绍二、创建 axios 函数对象1、创建 axios.js 文件2、创建 defaults.js 文件3、创建 _Axios.js 文件4、总结 当前篇章正式进入手写 axios 源码系列,我们要真枪实弹的开始写代码了。 因为 axios 源码的代码量比较庞大,所以我们这…...

HTB-Time
HTB-Time 信息收集80端口 立足pericles -> root 信息收集 80端口 有两个功能,一个是美化JSON数据。 一个是验证JSON,并且输入{“abc”:“abc”}之类的会出现报错。 Validation failed: Unhandled Java exception: com.fasterxml.jackson.core.JsonPa…...

零基础C/C++开发到底要学什么?
作者:黑马程序员 链接:https://www.zhihu.com/question/597037176/answer/2999707086 先和我一起看看,C/C学完了可以做什么: 软件工程师:负责设计、开发、测试和维护各类型的软件应用程序;游戏开发&#x…...

OpenStack中的CPU与内存超分详解
目录 什么是超分 CPU超分 查看虚拟机虚拟CPU运行在哪些物理CPU上 内存超分 内存预留 内存共享 如何设置内存预留和内存共享 全局设置 临时设置 什么是超分 超分通常指的是CPU或者GPU的分区或者分割,以在一个物理CPU或GPU内模拟多个逻辑CPU或GPU的功能。这…...

main.m文件解析--@autoreleasepool和UIApplicationMain
iOS 程序入口UIApplicationMain详解,相信大家新建一个工程的时候都会看到一个main.m文件,只不过我们很少了解它,现在我们分析一下它的作用是什么? 一、main.m文件 int main(int argc, char * argv[]) {autoreleasepool {return …...
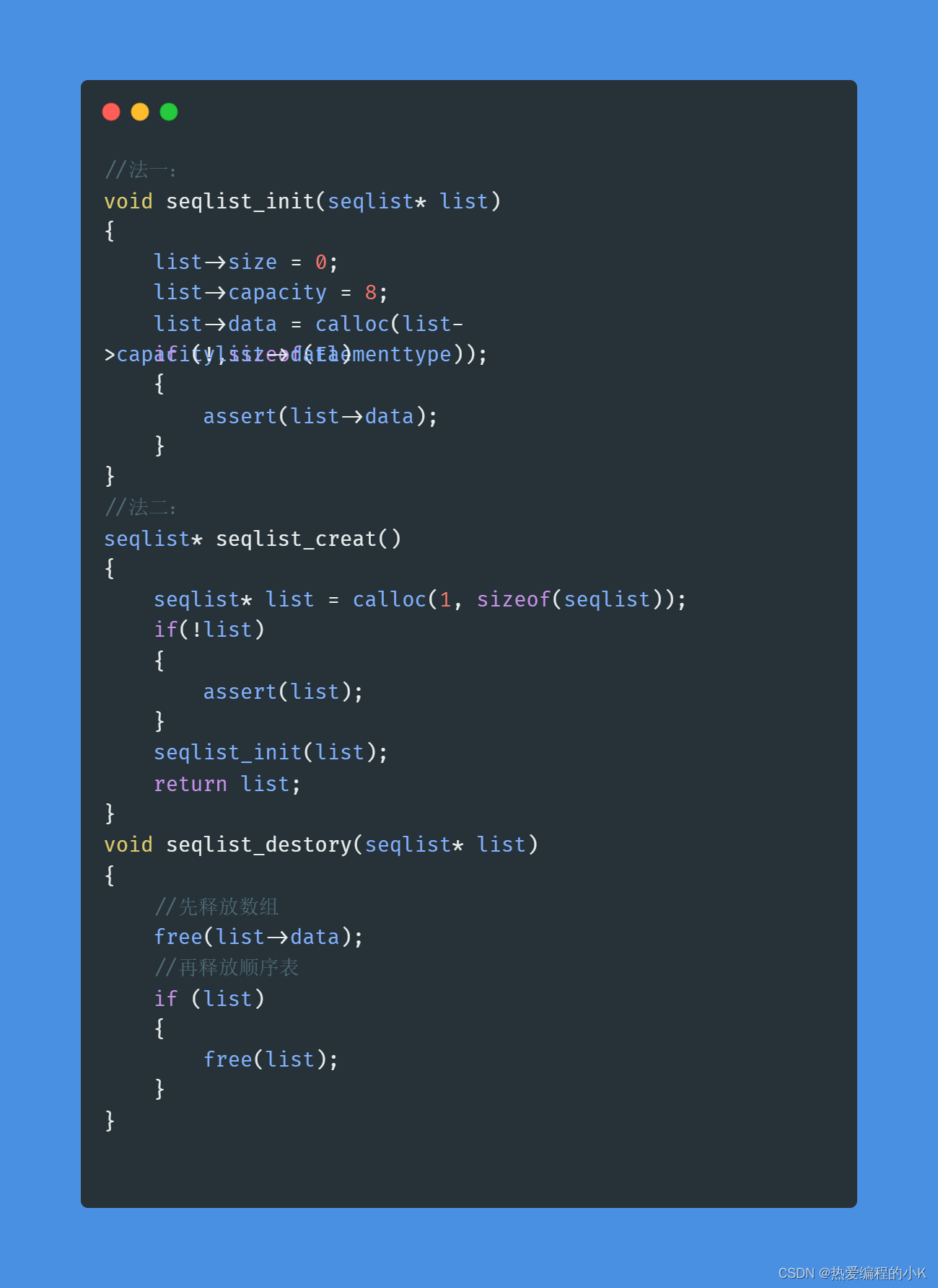
C语言复习之顺序表(十五)
📖作者介绍:22级树莓人(计算机专业),热爱编程<目前在c阶段>——目标C、Windows,MySQL,Qt,数据结构与算法,Linux,多线程,会持续分享…...
学系统集成项目管理工程师(中项)系列10_立项管理
1. 系统集成项目管理至关重要的一个环节 2. 重点在于是否要启动一个项目,并为其提供相应的预算支持 3. 项目建议 3.1. Request for Proposal, RFP 3.2. 立项申请 3.3. 项目建设单位向上级主管部门提交的项目申请文件,是对拟建项目提出的总体设想 3…...

电视盒子哪个好?数码小编盘点2023电视盒子排行榜
随着网络剧的热播,电视机又再度受宠,电视盒子也成为不可缺少的小家电。但面对复杂的参数和品牌型号,挑选时不知道电视盒子哪款最好,小编根据销量和用户评价整理半个月后盘点了电视盒子排行榜前五,对电视盒子哪个好感兴…...
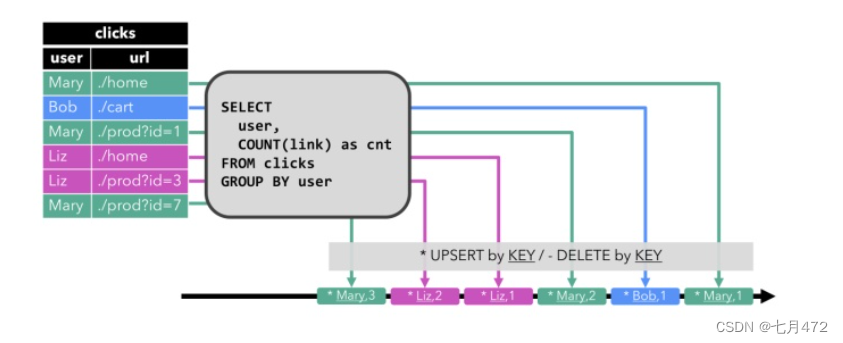
flink动态表的概念详解
目录 前言🚩 动态表和持续不断查询 stream转化成表 连续查询 查询限制 表转化为流 前言🚩 传统的数据库SQL和实时SQL处理的差别还是很大的,这里简单列出一些区别: 尽管存在这些差异,但使用关系查询和SQL处理流并…...

ArcGIS Pro用户界面
目录 1 功能区 1.1 快速访问工具栏 1.2 自定义快速访问工具栏 1.3 自定义功能区选项 1.3.1 添加组和命令 1.3.2 添加新选项卡 2 视图 3 用户界面排列 编辑 4 窗格 4.1 内容窗格 4.2 目录窗格 4.3 目录视图(类似ArcCatalog) 4.4 浏览对话框…...

HDCTF 2023 Pwn WriteUp
Index 前言Pwnner分析EXP: KEEP_ON分析EXP: Minions分析EXP: 后记: 前言 本人是菜狗,比赛的时候只做出来1题,2题有思路但是不会,还是太菜了。 栈迁移还是不会,但又都是栈迁移的题,真头大。得找时间好好学学…...

【 Spring 事务 】
文章目录 一、为什么需要事务(简单回顾)二、MySQL 中的事务使⽤三、Spring 中事务的实现3.1 Spring 编程式事务(手动事务)3.2 Spring 声明式事务(自动事务)3.2.1 Transactional 作⽤范围3.2.2 Transactional 参数说明3.2.3 Transactional 不进行事务回滚的情况3.2.4 Transactio…...
【刷题之路】LeetCode 203. 移除链表元素
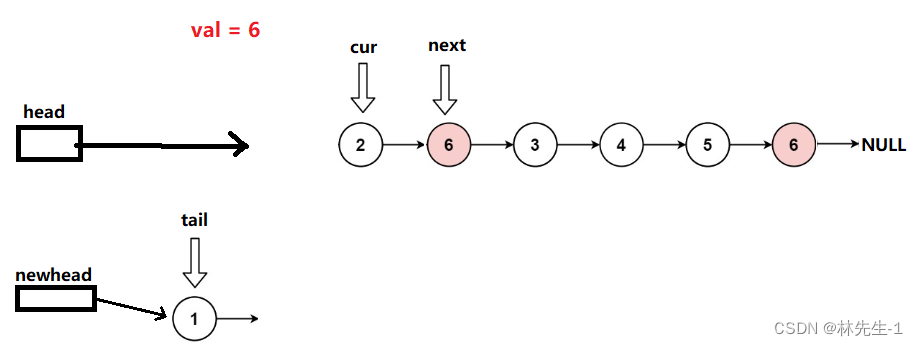
【刷题之路】LeetCode 203. 移除链表元素 一、题目描述二、解题1、方法1——在原链表上动刀子1.1、思路分析1.2、代码实现 2、方法2——使用额外的链表2.1、思路分析2.2、代码实现 一、题目描述 原题连接: 203. 移除链表元素 题目描述: 给你一个链表的…...
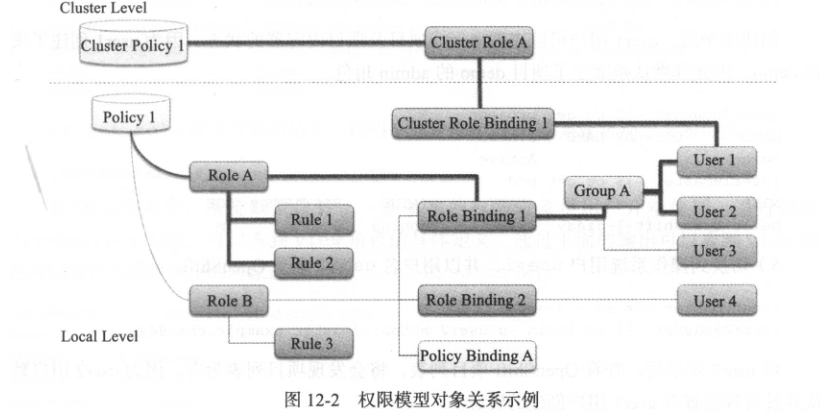
关于Open Shift(OKD) 中 用户认证、权限管理、SCC 管理的一些笔记
写在前面 因为参加考试,会陆续分享一些 OpenShift 的笔记博文内容为 openshift 用户认证和权限管理以及 scc 管理相关笔记学习环境为 openshift v3 的版本,有些旧这里如果专门学习 openshift ,建议学习 v4 版本理解不足小伙伴帮忙指正 对每个…...
)
活动文章测试(勿删)
大家好! 我是CSDN官方博客! 恭喜你正式加入CSDN博客,迈上技术成神之路~~ 路漫漫其修远兮——身为技术人,求索之路道阻且艰,但一万次的翘首却比不过一次的前行。 现在,就来开启你的个人博客,发布…...

synchronized 学习
学习源: https://www.bilibili.com/video/BV1aJ411V763?spm_id_from333.788.videopod.episodes&vd_source32e1c41a9370911ab06d12fbc36c4ebc 1.应用场景 不超卖,也要考虑性能问题(场景) 2.常见面试问题: sync出…...

2024年赣州旅游投资集团社会招聘笔试真
2024年赣州旅游投资集团社会招聘笔试真 题 ( 满 分 1 0 0 分 时 间 1 2 0 分 钟 ) 一、单选题(每题只有一个正确答案,答错、不答或多答均不得分) 1.纪要的特点不包括()。 A.概括重点 B.指导传达 C. 客观纪实 D.有言必录 【答案】: D 2.1864年,()预言了电磁波的存在,并指出…...

全球首个30米分辨率湿地数据集(2000—2022)
数据简介 今天我们分享的数据是全球30米分辨率湿地数据集,包含8种湿地亚类,该数据以0.5X0.5的瓦片存储,我们整理了所有属于中国的瓦片名称与其对应省份,方便大家研究使用。 该数据集作为全球首个30米分辨率、覆盖2000–2022年时间…...

Nginx server_name 配置说明
Nginx 是一个高性能的反向代理和负载均衡服务器,其核心配置之一是 server 块中的 server_name 指令。server_name 决定了 Nginx 如何根据客户端请求的 Host 头匹配对应的虚拟主机(Virtual Host)。 1. 简介 Nginx 使用 server_name 指令来确定…...

CMake 从 GitHub 下载第三方库并使用
有时我们希望直接使用 GitHub 上的开源库,而不想手动下载、编译和安装。 可以利用 CMake 提供的 FetchContent 模块来实现自动下载、构建和链接第三方库。 FetchContent 命令官方文档✅ 示例代码 我们将以 fmt 这个流行的格式化库为例,演示如何: 使用 FetchContent 从 GitH…...

Caliper 配置文件解析:config.yaml
Caliper 是一个区块链性能基准测试工具,用于评估不同区块链平台的性能。下面我将详细解释你提供的 fisco-bcos.json 文件结构,并说明它与 config.yaml 文件的关系。 fisco-bcos.json 文件解析 这个文件是针对 FISCO-BCOS 区块链网络的 Caliper 配置文件,主要包含以下几个部…...

有限自动机到正规文法转换器v1.0
1 项目简介 这是一个功能强大的有限自动机(Finite Automaton, FA)到正规文法(Regular Grammar)转换器,它配备了一个直观且完整的图形用户界面,使用户能够轻松地进行操作和观察。该程序基于编译原理中的经典…...

网站指纹识别
网站指纹识别 网站的最基本组成:服务器(操作系统)、中间件(web容器)、脚本语言、数据厍 为什么要了解这些?举个例子:发现了一个文件读取漏洞,我们需要读/etc/passwd,如…...

LLMs 系列实操科普(1)
写在前面: 本期内容我们继续 Andrej Karpathy 的《How I use LLMs》讲座内容,原视频时长 ~130 分钟,以实操演示主流的一些 LLMs 的使用,由于涉及到实操,实际上并不适合以文字整理,但还是决定尽量整理一份笔…...

tomcat指定使用的jdk版本
说明 有时候需要对tomcat配置指定的jdk版本号,此时,我们可以通过以下方式进行配置 设置方式 找到tomcat的bin目录中的setclasspath.bat。如果是linux系统则是setclasspath.sh set JAVA_HOMEC:\Program Files\Java\jdk8 set JRE_HOMEC:\Program Files…...
