【代码随想录训练营】【Day14】第六章|二叉树|理论基础|递归遍历|迭代遍历|统一迭代
理论基础
二叉树的定义形式有:节点指针和数组
- 在数组中,父节点的下标为
i,那么其左孩子的下标即i*2+1,右孩子的下标即为i*2+2
二叉树的常见遍历形式有:前序遍历、后序遍历、中序遍历和层序遍历
- 前序遍历:二叉树的节点遍历顺序为,根节点、左节点、右节点,常记为“根左右”
- 同理后序遍历则为“左右根”,中序遍历则为“左根右”,其主要的区别在于“根节点”的遍历顺序
- 但是注意,访问顺序和遍历顺序不是相同的概念,例如中序遍历应该理解为已访问过中节点,只是未处理它,需要优先处理它的左节点
- 层序遍历:顾名思义,就是按照从根节点到叶节点、从左到右的顺序,一层一层地遍历节点
根据二叉树的定义不同,又可分为不同类型的二叉树,常见的有:
- 满二叉树:只有度为0的结点和度为2的节点,并且度为0的结点都在同一层上。
- 完全二叉树:整颗树(包括其每一棵子树)
除了叶节点,其他每一个节点都有左右节点(节点不为空),同时要保证父子节点的顺序关系。 - 二叉搜索树:整颗树(包括其每一棵子树)都满足
左节点 < 父节点,右节点 > 父节点的条件,其中序遍历的结果为递增序列。 - 二叉平衡树:整颗树(包括其每一棵子树)每一个节点都满足
|其左右节点的树的高度的差值| <= 1
更多有关二叉树的理论基础可查阅:《代码随想录》二叉树理论基础
对于二叉树的遍历在《代码随想录》中都有非常详细的解释,我也是阅读学习之后再来解题的,所以在下面的解题过程中就不加以赘述了,仅贴出实现不同遍历形式的程序代码。
递归遍历二叉树
Java解法(递归,前序遍历):
class Solution {public List<Integer> preorderTraversal(TreeNode root) {List<Integer> ans = new ArrayList<>();this.preorder(root, ans);return ans;}public void preorder(TreeNode root, List<Integer> list){if(null == root){return;}list.add(root.val);this.preorder(root.left, list);this.preorder(root.right, list);}
}
Java解法(递归,中序遍历):
class Solution {public List<Integer> inorderTraversal(TreeNode root) {List<Integer> ans = new ArrayList<>();this.inorder(root, ans);return ans;}public void inorder(TreeNode root, List<Integer> list){if(null == root){return;}this.inorder(root.left, list);list.add(root.val);this.inorder(root.right, list);}
}
Java解法(递归,后序遍历):
class Solution {public List<Integer> postorderTraversal(TreeNode root) {List<Integer> ans = new ArrayList<>();this.postorder(root, ans);return ans;}public void postorder(TreeNode root, List<Integer> list){if(null == root){return;}this.postorder(root.left, list);this.postorder(root.right, list);list.add(root.val);}
}
迭代遍历二叉树
Java解法(迭代,前序遍历):
class Solution {public List<Integer> preorderTraversal(TreeNode root) {List<Integer> ans = new ArrayList<>();this.preorder(root, ans);return ans;}public void preorder(TreeNode root, List<Integer> list){Stack<TreeNode> stack = new Stack<>();if(null != root) stack.push(root);while(!stack.isEmpty()){root = stack.pop();list.add(root.val);if(null != root.right) stack.push(root.right);if(null != root.left) stack.push(root.left);}}
}
Java解法(迭代,中序遍历):
class Solution {public List<Integer> inorderTraversal(TreeNode root) {List<Integer> ans = new ArrayList<>();this.inorder(root, ans);return ans;}public void inorder(TreeNode root, List<Integer> list){Stack<TreeNode> stack = new Stack<>();while(null != root || !stack.isEmpty()){if(null != root){stack.push(root);root = root.left;}else{root = stack.pop();list.add(root.val);root = root.right;}}}
}
Java解法(迭代,后序遍历):
class Solution {public List<Integer> postorderTraversal(TreeNode root) {List<Integer> ans = new ArrayList<>();this.postorder(root, ans);return ans;}public void postorder(TreeNode root, List<Integer> list){Stack<TreeNode> stack = new Stack<>();if(null != root) stack.push(root);while(!stack.isEmpty()){root = stack.pop();list.add(root.val);if(null != root.left) stack.push(root.left);if(null != root.right) stack.push(root.right);}Collections.reverse(list);}
}
我们发现迭代法实现的先中后序,其实风格也不是那么统一,除了先序和后序,有关联,中序完全就是另一个风格了,一会用栈遍历,一会又用指针来遍历。那么如何针对三种不同的遍历方式,使用迭代法是可以写出统一风格的代码?
统一迭代遍历二叉树【重点】
可以利用标记法来做到统一迭代:
- 将访问的节点放入栈中,把要处理的节点也放入栈中但是要做标记。
- 在这里,我们利用空指针来做标记,在要处理的节点放入栈之后,紧接着放入一个空指针作为标记。
- 详细的解释和实现可以查阅:《代码随想录》二叉树的统一迭代法
Java解法(统一迭代,前序遍历):
class Solution {public List<Integer> preorderTraversal(TreeNode root) {List<Integer> ans = new ArrayList<>();this.preorder(root, ans);return ans;}public void preorder(TreeNode root, List<Integer> list){Stack<TreeNode> stack = new Stack<>();if(null != root) stack.push(root);while(!stack.isEmpty()){root = stack.peek();if(null != root){stack.pop(); // 需要先弹出节点,避免后续重复访问// 节点按照右左根的顺序进栈,后续出栈顺序为根左右(前序遍历)if(null != root.right) stack.push(root.right);if(null != root.left) stack.push(root.left);stack.push(root);stack.push(null); // 对需要处理的节点,在其后面跟上空指针作为标记}else{stack.pop(); // 遇到标记时,先弹出标记// 再弹出下一个节点进行处理root = stack.pop();list.add(root.val);}}}
}
Java解法(统一迭代,中序遍历):
class Solution {public List<Integer> inorderTraversal(TreeNode root) {List<Integer> ans = new ArrayList<>();this.inorder(root, ans);return ans;}public void inorder(TreeNode root, List<Integer> list){Stack<TreeNode> stack = new Stack<>();if(null != root) stack.push(root);while(!stack.isEmpty()){root = stack.peek();if(null != root){stack.pop(); // 需要先弹出节点,避免后续重复访问// 节点按照右根左的顺序进栈,后续出栈顺序为左根右(中序遍历)if(null != root.right) stack.push(root.right);stack.push(root);stack.push(null); // 对需要处理的节点,在其后面跟上空指针作为标记if(null != root.left) stack.push(root.left);}else{stack.pop(); // 遇到标记时,先弹出标记// 再弹出下一个节点进行处理root = stack.pop();list.add(root.val);}}}
}
Java解法(统一迭代,后序遍历):
class Solution {public List<Integer> postorderTraversal(TreeNode root) {List<Integer> ans = new ArrayList<>();this.postorder(root, ans);return ans;}public void postorder(TreeNode root, List<Integer> list){Stack<TreeNode> stack = new Stack<>();if(null != root) stack.push(root);while(!stack.isEmpty()){root = stack.peek();if(null != root){stack.pop();// 需要先弹出节点,避免后续重复访问// 节点按照根右左的顺序进栈,后续出栈顺序为左右根(后序遍历)stack.push(root);stack.push(null);// 对需要处理的节点,在其后面跟上空指针作为标记if(null != root.right) stack.push(root.right);if(null != root.left) stack.push(root.left);}else{stack.pop();// 遇到标记时,先弹出标记// 再弹出下一个节点进行处理root = stack.pop();list.add(root.val);}}}
}
二叉树结构也是在编程中常见的数据结构之一,例如堆其实就是一个树结构,以及哈希表中也运用到了红黑树来优化哈希表的存储结构等等。
通过今天的练习,我第一次了解并学习到了二叉树的统一迭代遍历算法,利用标记法来遍历二叉树的方法真的是非常巧妙,同时通过迭代算法的练习,也加深了对递归是如何模拟一个栈,以及递归算法如何转变为迭代算法有了一个初步的思路:
门径初窥书海奥, 欣喜若狂凯歌还。
相关文章:

【代码随想录训练营】【Day14】第六章|二叉树|理论基础|递归遍历|迭代遍历|统一迭代
理论基础 二叉树的定义形式有:节点指针和数组 在数组中,父节点的下标为i,那么其左孩子的下标即i*21,右孩子的下标即为i*22 二叉树的常见遍历形式有:前序遍历、后序遍历、中序遍历和层序遍历 前序遍历:二…...

AXI-Stream 学习笔记
参考 https://wuzhikai.blog.csdn.net/article/details/121326701 https://zhuanlan.zhihu.com/p/152283168 AXI4 介绍 AXI4 是ARM公司提出的一种片内总线,描述了主从设备之间的数据传输方式。主要有AXI4_LITE、AXI4_FULL、AXI4_STREAM三种。 AXI4_LITE࿱…...
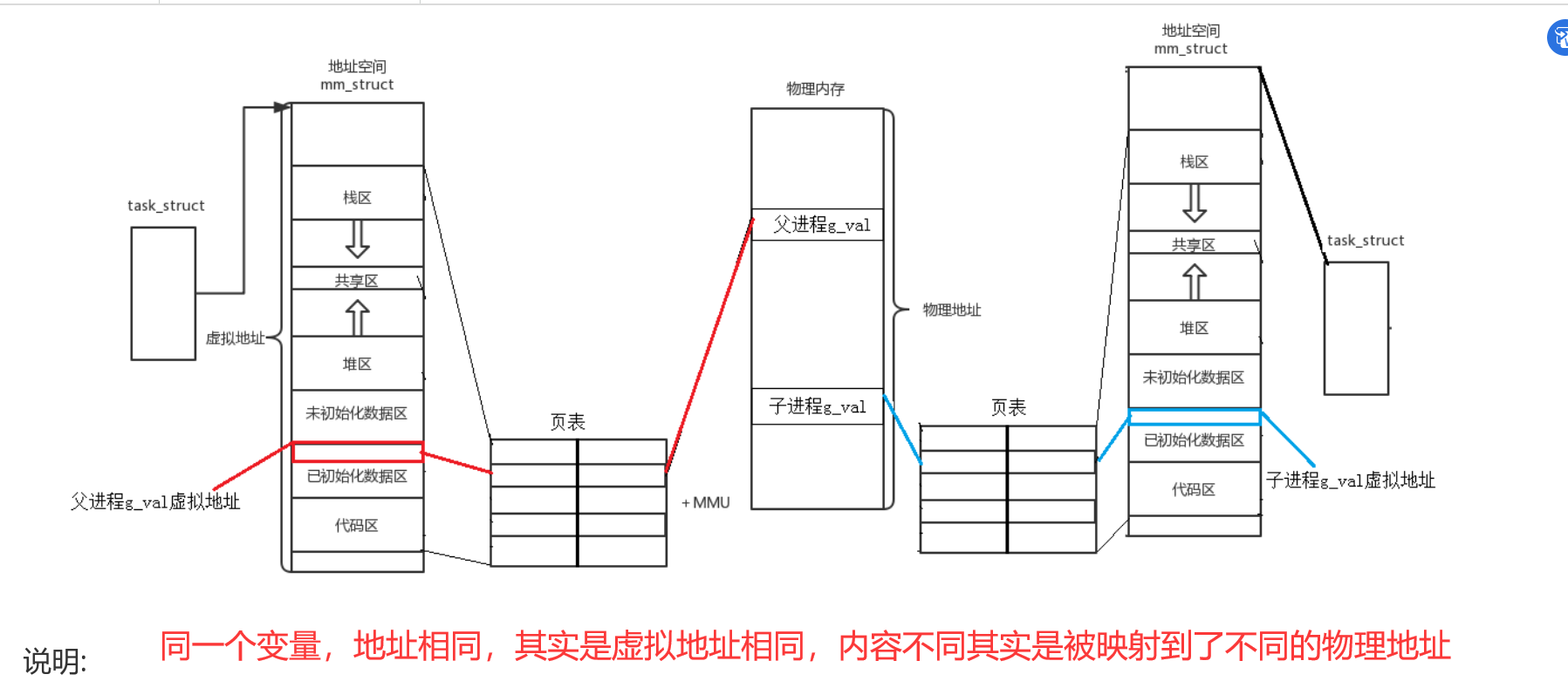
【Linux】程序进程地址空间
文章目录程序地址空间进程地址空间程序地址空间 在Linux下,这种地址叫做 虚拟地址, 我们在用C/C语言所看到的地址,全部都是虚拟地址!物理地址,用户一概看不到,由OS统一管理 问:C/C程序地址空间是内存吗? -> 根本就不是内存! 是进程虚拟地址空间 堆栈…...

电压放大器在液滴微流控芯片的功能研究中的应用
实验名称:电压放大器在液滴微流控芯片的功能研究中的应用研究方向:微流控生物芯片测试目的:液滴微流控技术能够在微通道内实现液滴生成,精准控制生成液滴的尺寸以及生成频率。结合芯片结构设计和外部控制条件,可以对液…...
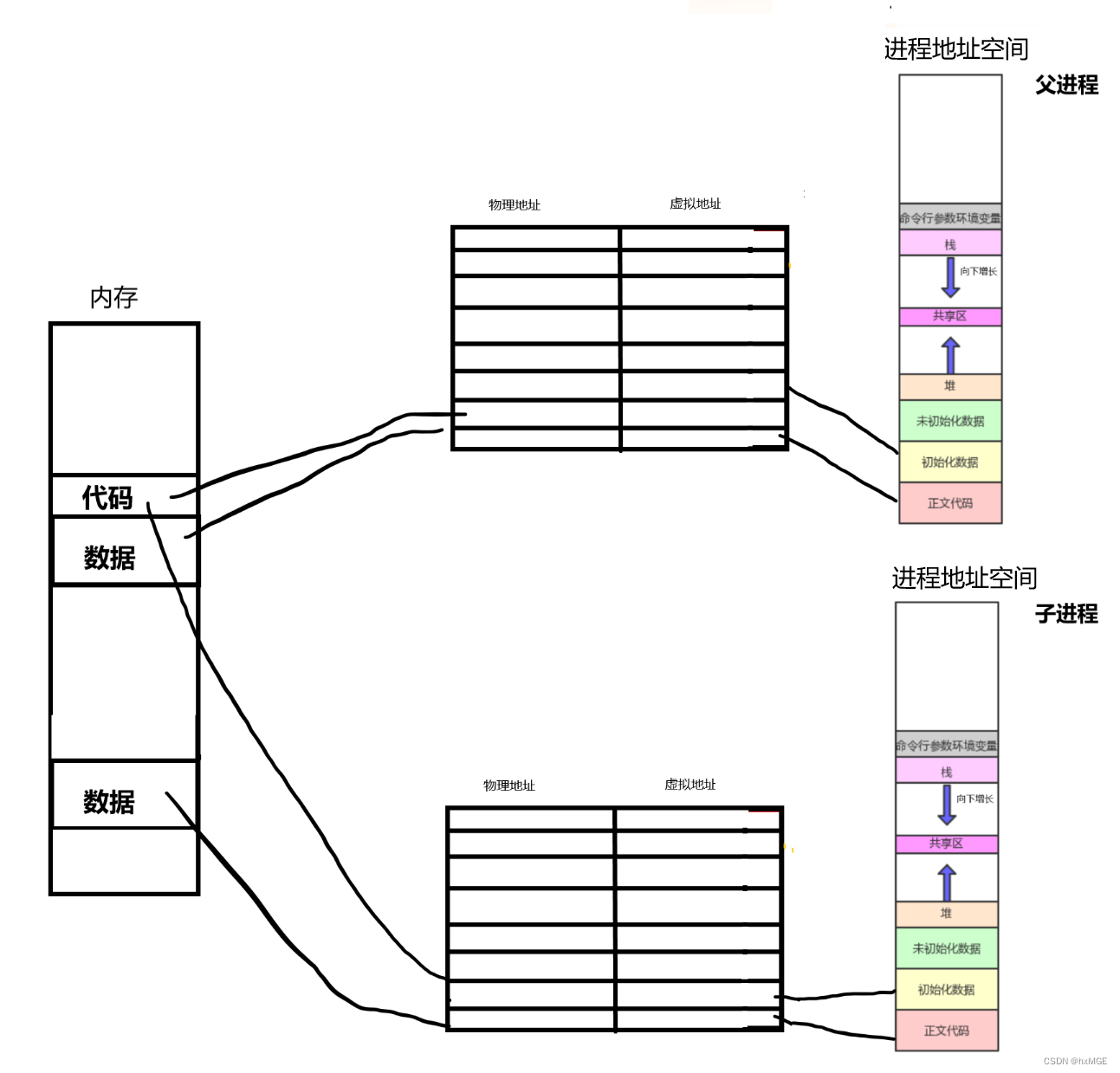
Linux操作系统学习(进程地址空间)
文章目录进程地址空间奇怪的现象什么是进程地址空间???虚拟地址是如何与物理内存联系的?页表是什么呢?为什么要有页表和地址空间,让进程直接访问内存不行吗?现象解释进程地址空间 在我们学习其…...

【排序】快速排序实现
目录 一、快速排序是什么? 二、左右指针法 1.实现原理 2.代码如下: 三、挖坑法 1.实现原理 2.代码如下: 四、前后指针法 1.实现原理 2.代码如下: 五、三数取中 1.实现思想 2.代码如下: 3.使用方法 总结…...

YOLOv5/v7 Flask Web 车牌识别 | YOLOv7 + EasyOCR 实现车牌识别
YOLOv7 Flask Web 车牌识别图片效果展示 本篇博文只包含源码以及使用方式,目前不同提供详细开发教程。 YOLOv7 Flask Web 车牌识别视频效果展示 YOLOv7 + EasyOCR 实现车牌识别 什么是Flask? 简介 Flask是一个轻量级的可定制框架,使用Python语言编写,较其他同类型框架更…...

【Opencv实战】几十年前的Vlog火了:黑白老照片如何上色?这黑科技操作一定要知道,复原度超高,竟美的出奇~(图像修复神级代码)
导语 哈喽大家好呀!我是每天疯狂赶代码的木木子吖~情人节快乐呀! 所有文章完整的素材源码都在👇👇 粉丝白嫖源码福利,请移步至CSDN社区或文末公众hao即可免费。 我们都知道,有很多经典的老照片…...

React源码分析(一)Fiber
前言 本次React源码参考版本为17.0.3。 React架构前世今生 查阅文档了解到, React16.x是个分水岭。 React15及之前 在16之前,React架构大致可以分为两层: Reconciler: 主要职责是对比查找更新前后的变化的组件;R…...
小樽 C++指针—— (壹) 指针变量
(壹) 指针变量 一、指针的概念与定义 二、给指针变量p赋值 三、指针变量的的、-运算 四、无类型指针 五、多重指针 C (壹) 指针变量 小明想把从李华家借来的书——《CCF中学生计算机程序设计》还给李华,但李华不在家,于是把书放到书架第3层的最右边…...
java 代码块 万字详解
概述 : 特点 : 格式 : 情景 : 细节 : 演示 : 英文 : //v,新版编辑器无手动添加目录的功能,PC端阅读建议通过侧边栏进行目录跳转;移动端建议用PC端阅读。😂一、概述 :代码块,也称为初始化块,属于类中的成员&…...
杂项-图片隐写
图片隐写的常见隐写方法: 三基色:RGB(Red Green Blue) 图片文件隐写 1.Firework 使用winhex打开文件时会看到文件头部中包含firework的标识,通过firework可以找到隐藏图片。 使用场景:查看隐写的图片文件…...

【高性价比】初学者入门吉他值得推荐购买的民谣单板吉他品牌—VEAZEN费森吉他
“在未知的世界里,我们是一群不疲不倦的行者,执念于真善美,热衷于事物的极致。我们抽丝剥茧,不断地打败自己,超越自己,我们无所畏惧终将成为巨人。”这是VEAZEN吉他官网首页上很明显的一段话,也…...
2023年浙江交安安全员考试题库及答案
百分百题库提供交安安全员考试试题、交安安全员考试真题、交安安全员证考试题库等,提供在线做题刷题,在线模拟考试,助你考试轻松过关。 50.根据《建设工程安全生产管理条例》第65条规定,施工单位有下列()行…...
)
【新】华为OD机试 - 跳格子(Python)
跳格子 题目 地上共有 N 个格子,你需要跳完地上所有的格子, 但是格子间是有强依赖关系的,跳完前一个格子后, 后续的格子才会被开启,格子间的依赖关系由多组 steps 数组给出, steps[0] 表示前一个格子, steps[1] 表示 steps[0] 可以开启的格子: 比如 [0,1] 表示从跳完第…...

乡村能做社区团购吗?怎么做?我走访调查后发现机会很大
乡村能做社区团购吗?怎么做?我走访调查后发现机会很大#深度触网 #社区团购 #乡村振兴##乡村旅游##县域经济##市场经济##农文旅产业振兴研究院#乡村旅游能带动农产品加工业、服务业、商贸业等相关联产业的发展 乡村能做社区团购吗?怎么做&…...

态路小课堂丨下一代数据中心100G接口第二篇——SFP-DD封装
100G光模块根据封装模式可分为QSFP28、CXP、CFP、CFP2、FCP4、DSFP和SFP-DD等。态路小课堂之前已经大量介绍了相关内容(。 态路小课堂丨下一代数据中心100G接口——DSFP态路小课堂丨100G解决方案-425G NRZ光模块态路小课堂丨什么是100G QSFP28单波光模块?…...

状态栏和导航栏高度获取
/*** 获取导航栏高度*/public static int getNavigationBarHeight(Context context){int navigationBarHeight 0;int resourceId context.getResources().getIdentifier("navigation_bar_height", "dimen", "android")if (resourceId > 0) {…...

插曲:第一桶金 1w 的来由
因为前天跟同事聊天,发现有个比较严重的认知,就是关于赚钱思维。 同事反馈说工作十来年,却没有接过私活,这里话分两头,有可能私 活钱少,但他给我的理由是:私活太麻烦,有时候不敢接&a…...

中国甲基异丁基甲醇行业头部企业市场占有率及排名调研报告
内容摘要 本文调研和分析全球甲基异丁基甲醇发展现状及未来趋势,核心内容如下: (1)全球市场总体规模,分别按销量和按收入进行了统计分析,历史数据2018-2022年,预测数据2023至2029年。 …...

使用docker在3台服务器上搭建基于redis 6.x的一主两从三台均是哨兵模式
一、环境及版本说明 如果服务器已经安装了docker,则忽略此步骤,如果没有安装,则可以按照一下方式安装: 1. 在线安装(有互联网环境): 请看我这篇文章 传送阵>> 点我查看 2. 离线安装(内网环境):请看我这篇文章 传送阵>> 点我查看 说明:假设每台服务器已…...

【大模型RAG】拍照搜题技术架构速览:三层管道、两级检索、兜底大模型
摘要 拍照搜题系统采用“三层管道(多模态 OCR → 语义检索 → 答案渲染)、两级检索(倒排 BM25 向量 HNSW)并以大语言模型兜底”的整体框架: 多模态 OCR 层 将题目图片经过超分、去噪、倾斜校正后,分别用…...

铭豹扩展坞 USB转网口 突然无法识别解决方法
当 USB 转网口扩展坞在一台笔记本上无法识别,但在其他电脑上正常工作时,问题通常出在笔记本自身或其与扩展坞的兼容性上。以下是系统化的定位思路和排查步骤,帮助你快速找到故障原因: 背景: 一个M-pard(铭豹)扩展坞的网卡突然无法识别了,扩展出来的三个USB接口正常。…...

零门槛NAS搭建:WinNAS如何让普通电脑秒变私有云?
一、核心优势:专为Windows用户设计的极简NAS WinNAS由深圳耘想存储科技开发,是一款收费低廉但功能全面的Windows NAS工具,主打“无学习成本部署” 。与其他NAS软件相比,其优势在于: 无需硬件改造:将任意W…...

C++_核心编程_多态案例二-制作饮品
#include <iostream> #include <string> using namespace std;/*制作饮品的大致流程为:煮水 - 冲泡 - 倒入杯中 - 加入辅料 利用多态技术实现本案例,提供抽象制作饮品基类,提供子类制作咖啡和茶叶*//*基类*/ class AbstractDr…...

Linux链表操作全解析
Linux C语言链表深度解析与实战技巧 一、链表基础概念与内核链表优势1.1 为什么使用链表?1.2 Linux 内核链表与用户态链表的区别 二、内核链表结构与宏解析常用宏/函数 三、内核链表的优点四、用户态链表示例五、双向循环链表在内核中的实现优势5.1 插入效率5.2 安全…...

MongoDB学习和应用(高效的非关系型数据库)
一丶 MongoDB简介 对于社交类软件的功能,我们需要对它的功能特点进行分析: 数据量会随着用户数增大而增大读多写少价值较低非好友看不到其动态信息地理位置的查询… 针对以上特点进行分析各大存储工具: mysql:关系型数据库&am…...

STM32+rt-thread判断是否联网
一、根据NETDEV_FLAG_INTERNET_UP位判断 static bool is_conncected(void) {struct netdev *dev RT_NULL;dev netdev_get_first_by_flags(NETDEV_FLAG_INTERNET_UP);if (dev RT_NULL){printf("wait netdev internet up...");return false;}else{printf("loc…...

linux 错误码总结
1,错误码的概念与作用 在Linux系统中,错误码是系统调用或库函数在执行失败时返回的特定数值,用于指示具体的错误类型。这些错误码通过全局变量errno来存储和传递,errno由操作系统维护,保存最近一次发生的错误信息。值得注意的是,errno的值在每次系统调用或函数调用失败时…...

Psychopy音频的使用
Psychopy音频的使用 本文主要解决以下问题: 指定音频引擎与设备;播放音频文件 本文所使用的环境: Python3.10 numpy2.2.6 psychopy2025.1.1 psychtoolbox3.0.19.14 一、音频配置 Psychopy文档链接为Sound - for audio playback — Psy…...
