【学习笔记】CF603E Pastoral Oddities
先不考虑数据结构部分,尝试猜一下结论。
结论:一个连通块有解当且仅当连通块的度数为偶数。
然后这题要你最大边权最小。最无脑的方法就是直接上 lct \text{lct} lct。真省事啊
我第一眼想到的还是整体二分。这玩意非常好写。
但是为什么也可以用线段树分治来做呢。这需要简单的分析一下性质。考虑求出每条边在哪些生成树上出现过,分析可知这一定是一段区间。
然后是非常玄学的操作。考虑离线,然后 倒着处理询问 (真是违背常理啊),这样的话一条边如果原来在生成树上,那么删去一条边后显然还是在生成树上(上面的分析告诉你的),这意味着恰好有一条边被加了进去,而这条边被加进去的条件就是连接的两个点不联通。
基于上述分析,我们可以尝试分治。首先,计算出影响区间的右端点在 [ m i d + 1 , r ] [mid+1,r] [mid+1,r]之间的边,那么我们就要先算出哪些边的影响区间 ≥ m i d + 1 \ge mid+1 ≥mid+1,哪些边的影响区间 ≤ m i d \le mid ≤mid,这样就将边集分成了两部分。使用可撤销并查集,然后往两边递归即可。怎么计算答案呢,发现递归到叶子节点的时候可以把那颗生成树算出来,然后就做完了。
事实上算边的影响区间部分我们可以不用真的将边分到两个集合中去。考虑更聪明的想法,倒着往前处理询问的时候,之前在生成树上的边还是在生成树上,那么我们事实上只需要在此基础上加入边权更大的边(当然这条边必须合法),直到得到的图满足条件。那么我们就知道新加入的这些边的影响区间的右端点就是当前这个位置,在线段树上对应部分打一个标记即可。这个半在线做法非常神奇。
这高级玩意估计考场上也想不到/kk
复杂度 O ( n log n log m ) O(n\log n\log m) O(nlognlogm)。
实现了后一种较为复杂的方法。
该死,有一个地方打挂了。
#include<bits/stdc++.h>
#define ll long long
#define fi first
#define se second
#define pb push_back
#define inf 0x3f3f3f3f
#define db double
#define cpx complex<db>
using namespace std;
const int N=3e5+5;
int n,m,cnt,res[N],now;
int fa[N],s[N],sa[N];
vector<int>G[N<<2];
struct node{int x,y,z;
}e[N];
bool cmp(int x,int y){return e[x].z<e[y].z;
}
int find(int x){return fa[x]==x?x:find(fa[x]);
}
void modify(int p,int l,int r,int ql,int qr,int x){if(ql>qr)return;if(ql<=l&&r<=qr){G[p].pb(x);return;}int mid=l+r>>1;if(ql<=mid)modify(p<<1,l,mid,ql,qr,x);if(mid<qr)modify(p<<1|1,mid+1,r,ql,qr,x);
}
void solve(int p,int l,int r){vector<pair<int,int>>bak;for(auto pos:G[p]){int x=find(e[pos].x),y=find(e[pos].y);if(x!=y){cnt-=(s[x]&1)+(s[y]&1);if(s[x]>s[y])swap(x,y);bak.pb(make_pair(x,y));fa[x]=y,s[y]+=s[x],cnt+=(s[y]&1);}}if(l==r){while(cnt&&now<=m){int x=find(e[sa[now]].x),y=find(e[sa[now]].y);if(sa[now]<l)modify(1,1,m,sa[now],l-1,sa[now]);//fixedif(sa[now]<=l&&x!=y){cnt-=(s[x]&1)+(s[y]&1);if(s[x]>s[y])swap(x,y);bak.pb(make_pair(x,y));fa[x]=y,s[y]+=s[x],cnt+=(s[y]&1);}now++;}if(!cnt)res[l]=e[sa[now-1]].z;else res[l]=-1;}else{int mid=l+r>>1;solve(p<<1|1,mid+1,r);solve(p<<1,l,mid);}reverse(bak.begin(),bak.end());for(auto x:bak){cnt-=s[x.se]&1;fa[x.fi]=x.fi,s[x.se]-=s[x.fi];cnt+=(s[x.fi]&1)+(s[x.se]&1);}
}
int main(){ios::sync_with_stdio(false);cin.tie(0),cout.tie(0);cin>>n>>m;for(int i=1;i<=n;i++)fa[i]=i,s[i]=1;for(int i=1;i<=m;i++){cin>>e[i].x>>e[i].y>>e[i].z,sa[i]=i;}sort(sa+1,sa+1+m,cmp);cnt=n,now=1;solve(1,1,m);for(int i=1;i<=m;i++)cout<<res[i]<<"\n";
}
相关文章:

【学习笔记】CF603E Pastoral Oddities
先不考虑数据结构部分,尝试猜一下结论。 结论:一个连通块有解当且仅当连通块的度数为偶数。 然后这题要你最大边权最小。最无脑的方法就是直接上 lct \text{lct} lct。真省事啊 我第一眼想到的还是整体二分。这玩意非常好写。 但是为什么也可以用线段…...
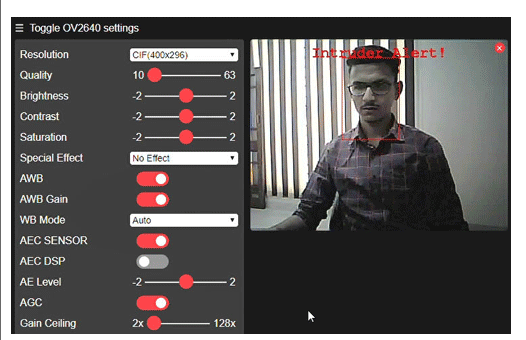
如何使用ESP32-CAM构建一个人脸识别系统
有许多人识别系统使用签名、指纹、语音、手部几何、人脸识别等来识别人,但除了人脸识别系统。 人脸识别系统不仅可以用于安全目的来识别公共场所的人员,还可以用于办公室和学校的考勤目的。 在这个项目中,我们将使用 ESP32-CAM 构建一个人脸识…...

JavaWeb分页条件查询参数特殊字符处理
问题背景 在项目开发过程中,基本都会有列表条件查询,例如用户管理会有通过用户姓名模糊查询用户,课程管理会有课程名称模糊查询课程等等。 而查询过程中如果用户在界面上输入一些特殊字符,例如:%_等等,这…...

ubuntu18服务安装
一、JDK安装 将jdk解压缩到该目录 /opt/ sudo tar -zxvf jdk-8u261-linux-x64.tar.gz -C /opt/ #重命名 cd /opt sudo mv jdk-8u261-linux-x64 jdk_8 修改环境变量 sudo vi ~/.bashrc #在文件最后追加以下文本 #进入编辑器后输入以下指令: #1. G //将光标移到最后一…...

这些使用工具大推荐,现在知道不晚
1.Snip Snip是一款截图软件,它突出的优点就是可以制作滚动截图。 例如:对整个网页进行截图,使用Snip即可轻松获取,无需处理水印。 2.Sleep Cycle 快节奏、高压力的生活导致我们越来越晚睡觉,睡眠质量越来越差。 想提…...

【Java|golang】1048. 最长字符串链
给出一个单词数组 words ,其中每个单词都由小写英文字母组成。 如果我们可以 不改变其他字符的顺序 ,在 wordA 的任何地方添加 恰好一个 字母使其变成 wordB ,那么我们认为 wordA 是 wordB 的 前身 。 例如,“abc” 是 “abac”…...

Hive基础和使用详解
文章目录 一、启动hive1. hive启动的前置条件2. 启动方式一: hive命令3. 方式二:使用jdbc连接hive 二、Hive常用交互命令1. hive -help 命令2. hive -e 命令3. hive -f 命令4. 退出hive窗口5. 在hive窗口中执行dfs -ls /; 三、Hive语法1.DDL语句1.1 创建数据库1.2 两…...

c/c++:栈帧,传值,传址,实参传值给形参,传地址指针给形参
c/c:栈帧,传值,传址,实参传值给形参,传地址指针给形参 2022找工作是学历、能力和运气的超强结合体,遇到寒冬,大厂不招人,此时学会c的话, 我所知道的周边的会c的同学&…...
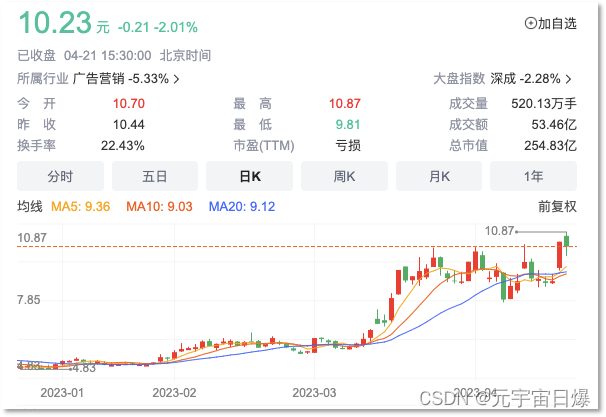
玩元宇宙血亏后 蓝色光标梭哈AI也挺悬
蓝色光标2022年年度报告出炉,巨亏21.75 亿元,其中20.38亿亏损因商誉、无形资产及其他资产减值造成,而在实际亏损业务中,元宇宙占比不小。 蓝色光标在元宇宙领域的布局,主要通过三家子公司实施,分别为蓝色宇…...

生物---英文
标题 前言必学场景词汇及用法鸟类昆虫类哺乳类爬行类情境常用单词鸟类虫类哺乳类两栖类与爬行类分类与动物相关的习语前言 加油 必学场景词汇及用法 鸟类 1bird [b[插图]d] n.鸟bird’s-eye-view[ˈb[插图]dzaɪˌvju]adj.鸟瞰图的a bird’s-eye view鸟瞰a flock of bird…...

ENVI 国产高分2号(GF-2)卫星数据辐射定标 大气校正 影像融合
1.数据 高分2号卫星数据,包含: MSS-1\2多光谱数据,4m分辨率; Pan-1\2全色波段数据,0.8m分辨率。 2.处理软件 ENVI5.3 国产插件下载地址:ENVI App Store (geoscene.cn) 首先下载插件文件; …...

操作系统考试复习——第二章 进程控制 同步与互斥
进程控制一般是由OS中的原语来实现的。 大多数OS内核都包含了两大方面的功能: 1.支撑功能:1)中断处理 2)时钟管理 3)原语操作(原语操作就是原子操作。所谓原子操作就是一个操作中所有动作要不全做要不全不做) 2.资源管理功能:1)进程管理…...
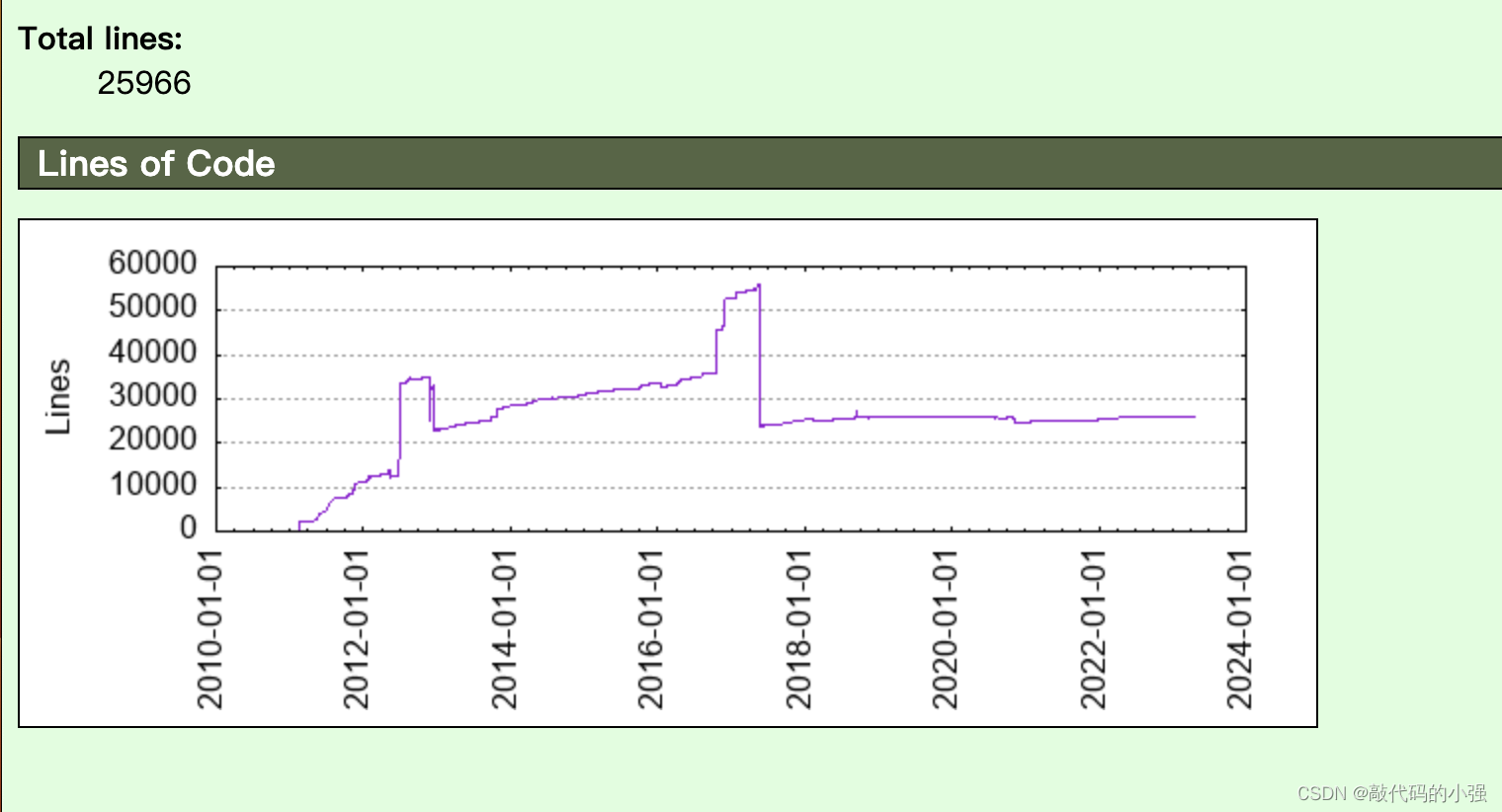
mac gitstats查看git提交记录
一、介绍: 进一步来讲,Gitstats它是一个git仓库分析软件,它可以检查仓库并生成历史数据的统计信息。可以帮助你查看git仓库的提交状态,根据不同维度分析计算,并自动生成数据图表。 官网介绍:http://gitst…...
电脑系统错误怎么办?您可以看看这5个方法!
案例:电脑出现系统错误该如何解决? 【这几天长时间使用我的电脑,导致它的系统出现了错误。有没有小伙伴知道如何解决电脑系统出错的问题?求一个能快速解决的方法。】 电脑系统出现错误是使用电脑时难免会遇到的问题之一…...

九款顶级AI工具推荐
ChatGPT OpenAI开发的最强对话系统 地址:chat.openai.com ChatGPT能够在同一个会话期间内回答上下文相关的后续问题。其在短时间内引爆全球的原因在于,在网友们晒出的截图中,ChatGPT不仅能流畅地与用户对话,甚至能写诗、撰文、编…...

StringRedisTemplate-基本使用
StringRedisTemplate继承自RedisTemplate,在这里说明一下,当我们使用RedisTemplate往redis中存储java对象的时候,他会顺带着将该java对象的字节码文件也同时存进了内存中,这是为了实现自动反序列化Autowired private StringRedisTemplate red…...

ansible自动运维——ansible使用临时命令通过模块来执行任务
大家好,这里是天亮之前ict,本人网络工程大三在读小学生,拥有锐捷的ie和红帽的ce认证。每天更新一个linux进阶的小知识,希望能提高自己的技术的同时,也可以帮助到大家 另外其它专栏请关注: 锐捷数通实验&…...
)
python 之数据类型(四)
1、字符串(String) 使用双引号或者单引号中的数据,就是字符串 注:python中使用三引号时允许一个字符串跨多行,字符串中可以包含换行符、制表符以及其它特殊符号 a a c g print(a)运行结果: a c g1、下标 …...

洛谷P1345 无向图最小割点数
题意: 给出一副有 n n n个点, m m m条边的无向图,求出这副图的最小割点数 题意: 首先对于有向图,求他的最小割边,只需要令每条边的容量为 1 1 1,求出起点到终点的最大流就是最小割边数了。 容…...

适合程序员阅读的有用书籍:
几本适合程序员阅读的有用书籍: 1.《计算机程序设计艺术》(The Art of Computer Programming)是由Donald E. Knuth撰写的一系列著作,是计算机科学领域的经典之作。该系列著作共分为三卷,分别介绍了算法和计算机程序设计的基础知识和技巧。 …...
详解)
后进先出(LIFO)详解
LIFO 是 Last In, First Out 的缩写,中文译为后进先出。这是一种数据结构的工作原则,类似于一摞盘子或一叠书本: 最后放进去的元素最先出来 -想象往筒状容器里放盘子: (1)你放进的最后一个盘子(…...

浅谈 React Hooks
React Hooks 是 React 16.8 引入的一组 API,用于在函数组件中使用 state 和其他 React 特性(例如生命周期方法、context 等)。Hooks 通过简洁的函数接口,解决了状态与 UI 的高度解耦,通过函数式编程范式实现更灵活 Rea…...

iOS 26 携众系统重磅更新,但“苹果智能”仍与国行无缘
美国西海岸的夏天,再次被苹果点燃。一年一度的全球开发者大会 WWDC25 如期而至,这不仅是开发者的盛宴,更是全球数亿苹果用户翘首以盼的科技春晚。今年,苹果依旧为我们带来了全家桶式的系统更新,包括 iOS 26、iPadOS 26…...

在rocky linux 9.5上在线安装 docker
前面是指南,后面是日志 sudo dnf config-manager --add-repo https://download.docker.com/linux/centos/docker-ce.repo sudo dnf install docker-ce docker-ce-cli containerd.io -y docker version sudo systemctl start docker sudo systemctl status docker …...

uni-app学习笔记二十二---使用vite.config.js全局导入常用依赖
在前面的练习中,每个页面需要使用ref,onShow等生命周期钩子函数时都需要像下面这样导入 import {onMounted, ref} from "vue" 如果不想每个页面都导入,需要使用node.js命令npm安装unplugin-auto-import npm install unplugin-au…...

Python爬虫实战:研究feedparser库相关技术
1. 引言 1.1 研究背景与意义 在当今信息爆炸的时代,互联网上存在着海量的信息资源。RSS(Really Simple Syndication)作为一种标准化的信息聚合技术,被广泛用于网站内容的发布和订阅。通过 RSS,用户可以方便地获取网站更新的内容,而无需频繁访问各个网站。 然而,互联网…...

unix/linux,sudo,其发展历程详细时间线、由来、历史背景
sudo 的诞生和演化,本身就是一部 Unix/Linux 系统管理哲学变迁的微缩史。来,让我们拨开时间的迷雾,一同探寻 sudo 那波澜壮阔(也颇为实用主义)的发展历程。 历史背景:su的时代与困境 ( 20 世纪 70 年代 - 80 年代初) 在 sudo 出现之前,Unix 系统管理员和需要特权操作的…...

什么?连接服务器也能可视化显示界面?:基于X11 Forwarding + CentOS + MobaXterm实战指南
文章目录 什么是X11?环境准备实战步骤1️⃣ 服务器端配置(CentOS)2️⃣ 客户端配置(MobaXterm)3️⃣ 验证X11 Forwarding4️⃣ 运行自定义GUI程序(Python示例)5️⃣ 成功效果
Java 二维码
Java 二维码 **技术:**谷歌 ZXing 实现 首先添加依赖 <!-- 二维码依赖 --><dependency><groupId>com.google.zxing</groupId><artifactId>core</artifactId><version>3.5.1</version></dependency><de…...

AI,如何重构理解、匹配与决策?
AI 时代,我们如何理解消费? 作者|王彬 封面|Unplash 人们通过信息理解世界。 曾几何时,PC 与移动互联网重塑了人们的购物路径:信息变得唾手可得,商品决策变得高度依赖内容。 但 AI 时代的来…...
