数据结构 | 树 | 二叉树
🔥Go for it!🔥
📝个人主页:按键难防
📫 如果文章知识点有错误的地方,请指正!和大家一起学习,一起进步👀📖系列专栏:数据结构与算法
🔥 如果感觉博主的文章还不错的话,还请 点赞👍🏻收藏⭐️ + 留言📝支持 一下博主哦
目录
树
二叉树:
二叉树定义方法(链式存储):
层次建树实战:
①辅助队列(链式存储实现):
②建树(源码):
二叉树的遍历:
①前序遍历
②中序遍历
③后序遍历
④层次遍历
汇总:

树
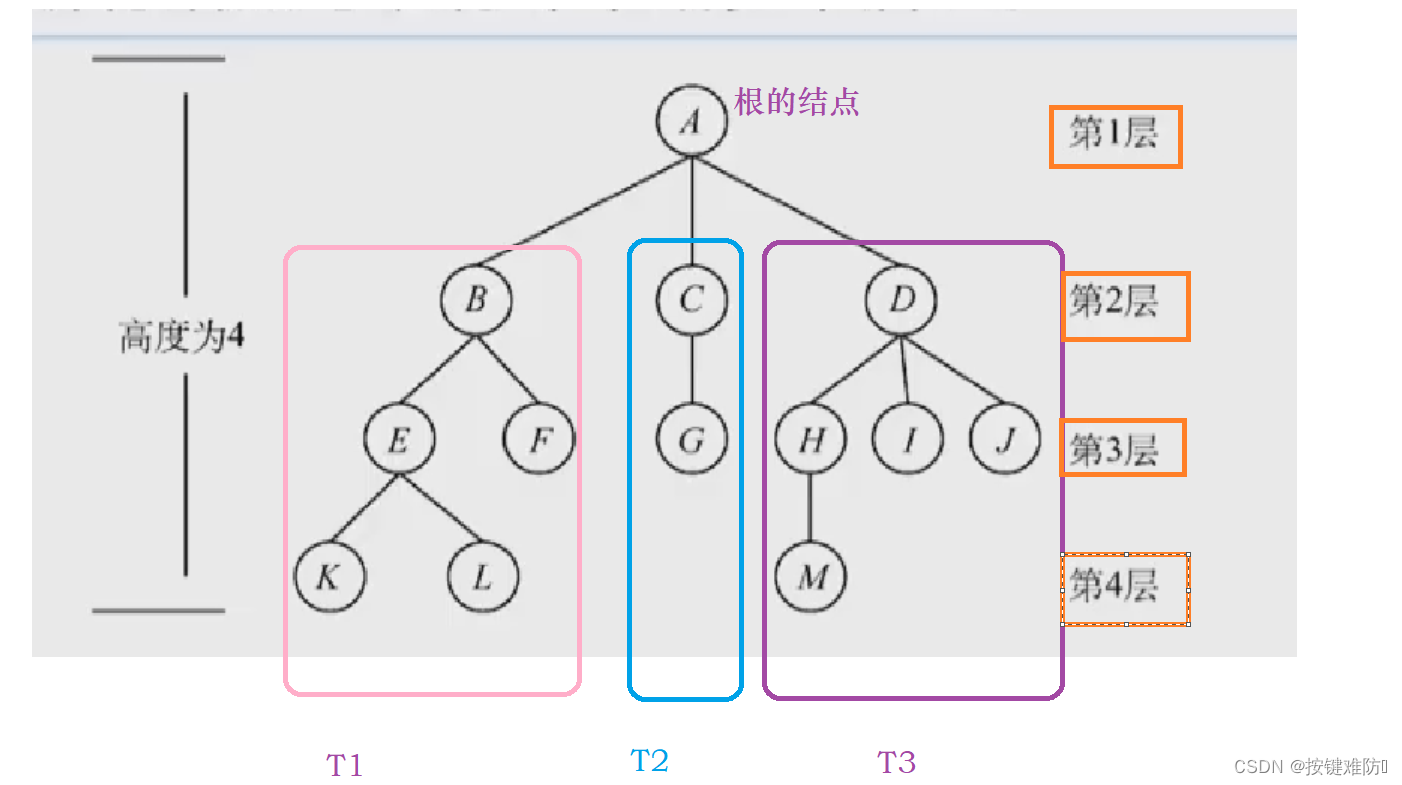
树是n(n ≥ 0)个节点的有限集。当n = 0时,称为空树。在任意一棵非空树中应满足:
1)有且仅有一个特定的结点的称为根的结点。
2)当n > 1时,其余节点可分为m(m > 0)个 互不相交的有限集T1, T2,…, Tm,其中每个集合 本身又是一棵树,并且称为根的子树。
特点:
树作为一种逻辑结构,同时也是一种分层结构,具 有以下两个特点:
1)树的根结点没有前驱,除根结点外的所有结点有且只有一个前驱。
2)树中所有结点可以有零个或多个后继。
二叉树:
二叉树是另一种树形结构,其特点是每个结点至多只有两棵子树 (即二叉树中不存在度大于2的结点),并且二叉树的子树有左右之分,其次序不能任意颠倒。 与树相似,二叉树也以递归的形式定义。二叉树是n(n ≥ 0)个 结点的有限集合:
① 或者为空二叉树,即n = 0。
② 或者由一个根结点和两个互不相交的被称为根的左子树和右子树组成。左子树和右子树又分别是一棵二叉树。
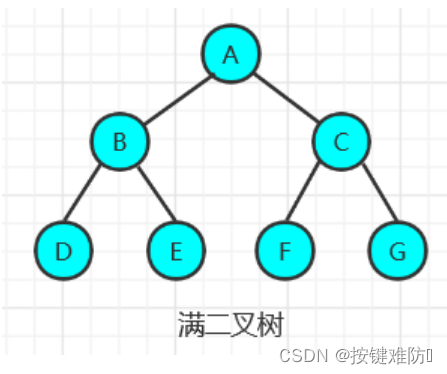
满二叉树:
在一颗二叉树中,如果所有分支结点都有左子结点和右子结点,并且叶结点都集中在二叉树的最底层,这样的二叉树称为满二叉树。
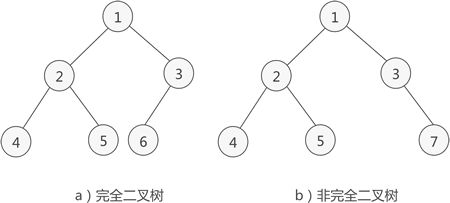
完全二叉树:
完全二叉树是由满二叉树引出的。满二叉树要求每一层的节点数都达到最大值,完全二叉树仅要求除最后一层外的节点数达到最大值,也就是说最后一层可以不满。但是最后一层从左往右不能有中断。
二叉树定义方法(链式存储):
typedef char BiElemType;
typedef struct BiTNode{BiElemType c;//c就是书籍上的datastruct BiTNode *lchild;//该二叉树的左孩子struct BiTNode *rchild;//该二叉树的右孩子
}BiTNode, *BiTree;
解释:typedef重命名了两个数据类型,
分别是将struct BiTNode重命名为BiTNode,将struct BiTNode*重命名为BiTree
前者是个结构体,后者是个指向该结构体的指针
用BiTNode创建变量,就是创建一个结构体(树的结点)
用BiTree创建变量,就是指向这个结构体的指针,用于接受动态内存开辟返回的指针层次建树实战:
将"abcdefghij"用二叉树的方式存起来。
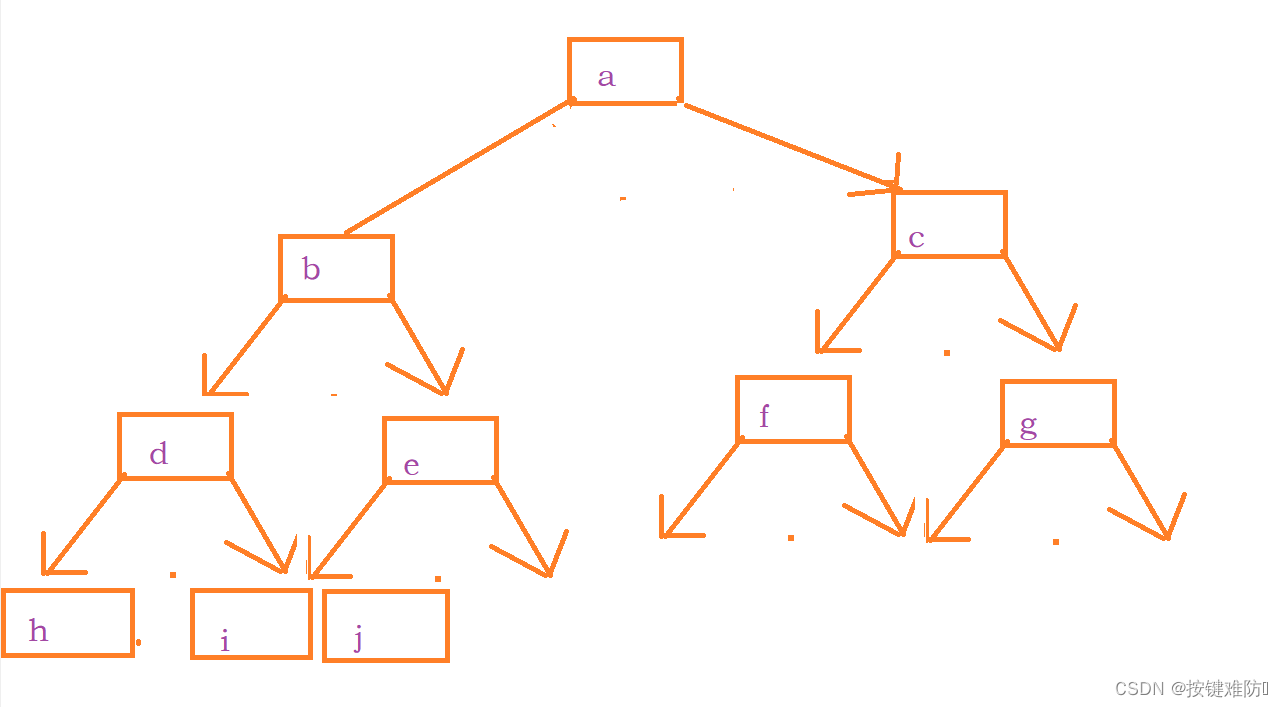
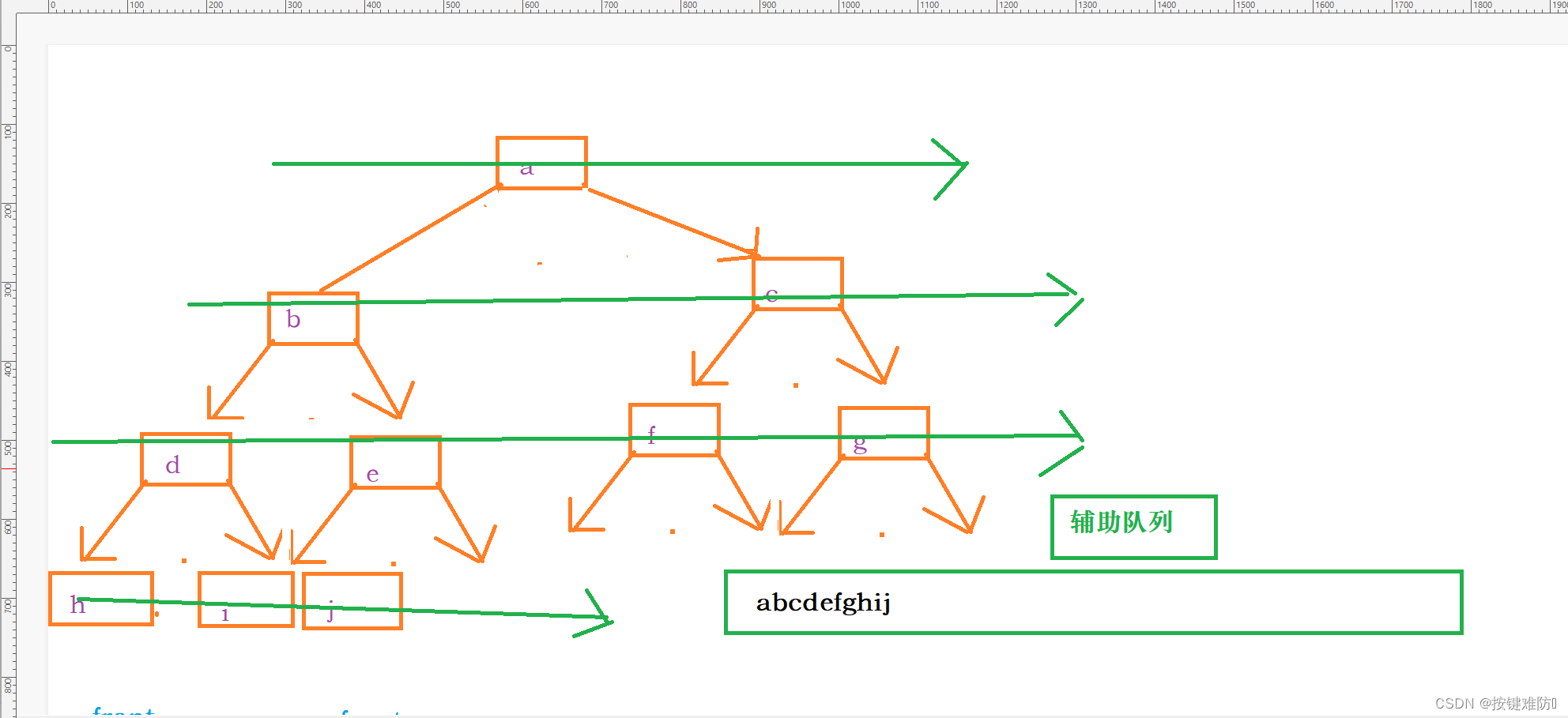
①辅助队列(链式存储实现):
每多一个分支就当做一个元素入队,每当一个结点都有左右孩子,出队该节点。
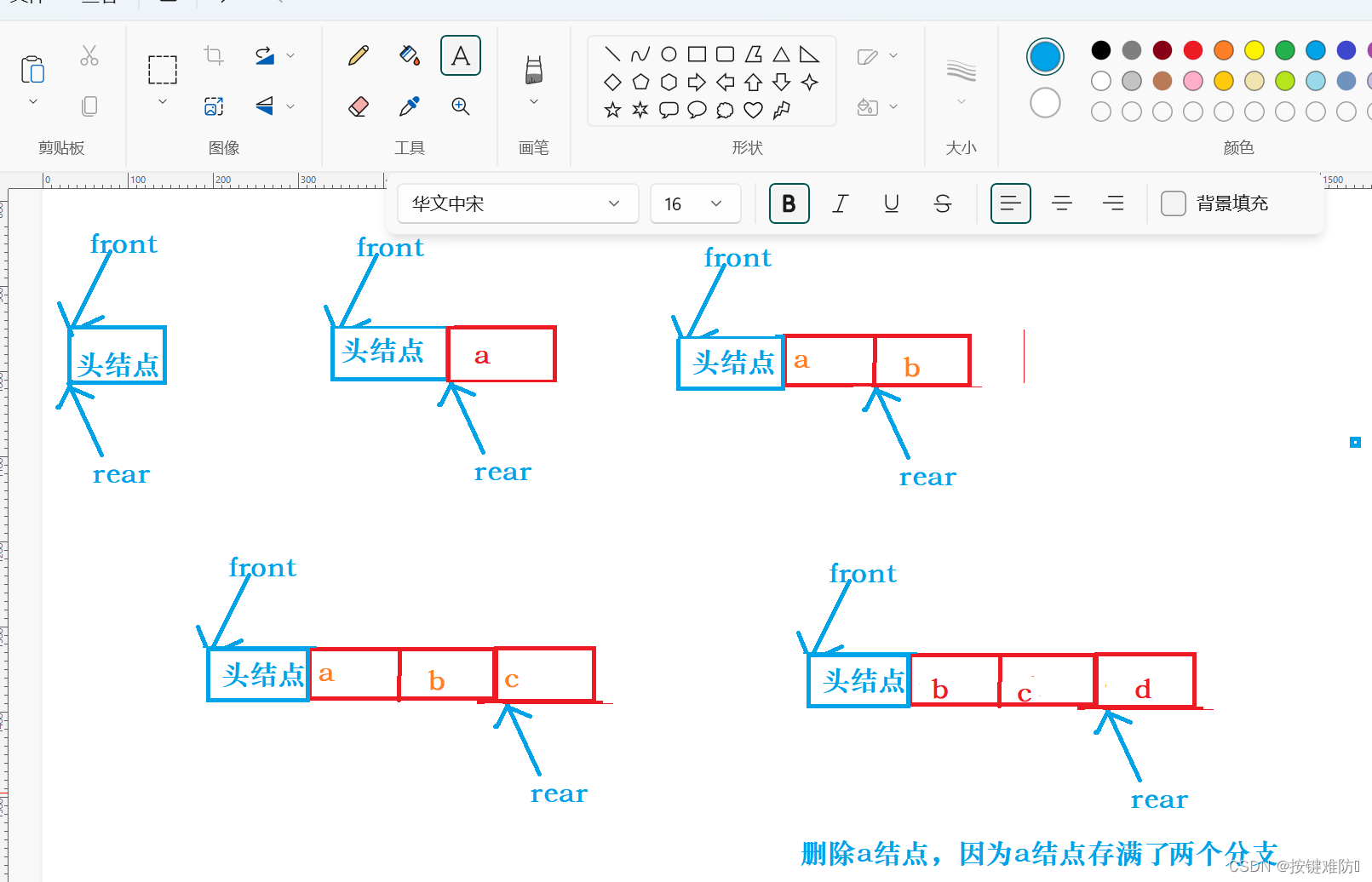
所以只要满3个结点,就说明有一个树的结点存满两个分支,这样就需要删除第一个结点。
保证第一个结点始终不满两个分支。
实现:
typedef struct LinkNode//LinkNode结构体是辅助队列的结点
{BiTree p;//数据域,存放树的结点的地址值struct LinkNode *next;//指针域,辅助队列中下一个结点
}LinkNode;
typedef struct//结构体,用于存放辅助队列头结点和队列尾结点的指针
{ LinkNode* front, *rear;
}LinkQueue;
void InitQueue(LinkQueue &Q) //初始化头尾指针,就是创建头结点,然后头尾指针都指向这一头结点
{Q.front = Q.rear = (LinkNode*)malloc(sizeof(LinkNode));//为辅助队列头结点申请空间//初始化时头尾指针都指向这一头结点Q.front->next = NULL;//头结点的next指针为NULL
}
void EnQueue(LinkQueue&Q, BiTree x)//入队,尾部插入法
{LinkNode *s = (LinkNode *)malloc(sizeof(LinkNode));//为入队的元素申请空间s->p = x; s->next = NULL;//新申请的结点作为最后一个结点Q.rear->next =s;//先让前一结点(Q.rear)的指针域指向新插入的结点Q.rear = s;//然后再让Q.rear变为指向尾部的那个结点
}
//出队 头部删除法
bool DeQueueF(LinkQueue &Q)
{//front始终指向头结点,但头结点什么都没存LinkNode *q = Q.front->next;//将第一个节点存入qQ.front->next = q->next;//断链,保留第一个结点的指针域,让头节点指向第二个结点free(q);return true;
}②建树(源码):
注释的很详细
#include <stdio.h>
#include <stdlib.h>
typedef char BiElemType;
typedef struct BiTNode{BiElemType data;struct BiTNode *lchild;struct BiTNode *rchild;
}BiTNode, *BiTree;
typedef struct LinkNode//LinkNode结构体是辅助队列的结点
{BiTree p;//树的某一个结点的地址值,不是数值struct LinkNode *next;//辅助队列中下一个结点
}LinkNode;
typedef struct //结构体,用于存放辅助队列头结点和队列尾结点的指针
{ LinkNode* front, *rear;
}LinkQueue;
void InitQueue(LinkQueue &Q) //初始化头尾指针,就是创建头结点,然后头尾指针都指向这一头结点
{Q.front = Q.rear = (LinkNode*)malloc(sizeof(LinkNode));//为辅助队列头结点申请空间//初始化时头尾指针都指向这一头结点Q.front->next = NULL;//头结点的next指针为NULL
}
void EnQueue(LinkQueue&Q, BiTree x)//入队,尾部插入法
{LinkNode *s = (LinkNode *)malloc(sizeof(LinkNode));//为入队的元素申请空间s->p = x; s->next = NULL;//新申请的结点作为最后一个结点Q.rear->next =s;//先让前一结点(Q.rear)的指针域指向新插入的结点Q.rear = s;//然后再让Q.rear变为指向尾部的那个结点
}
//出队 头部删除法
bool DeQueueF(LinkQueue &Q)
{//front始终指向头结点,但头结点什么都没存LinkNode *q = Q.front->next;//将第一个节点存入qQ.front->next = q->next;//断链,保留第一个结点的指针域,让头节点指向第二个结点free(q);return true;
}
int main()//二叉树的建树(层次建树)
{LinkQueue Q;//创建辅助队列头尾指针InitQueue(Q);//初始化头尾指针BiTree pnew;//用来指向新申请的树结点的指针BiTree tree = NULL;//树根的指针char c;//输入内容为 abcdefghijwhile (scanf("%c", &c)){if (c == '\n'){break;}pnew = (BiTree)calloc(1, sizeof(BiTNode));//calloc申请空间并对空间进行初始化,赋值为0pnew->data = c;//数据放进去EnQueue(Q, pnew);//将新创建的树的结点的地址入队辅助队列//下面是建树的过程if (NULL == tree)//空树{tree = pnew; //tree指向树的根节点continue;//该节点为树的第一个节点//直接跳到循环的判断部分}else {if (NULL == Q.front->next->p->lchild)//如何把新结点放入树{//Q.front->next为辅助队列第一个结点Q.front->next->p->lchild = pnew;//把新结点放到要插入结点的左边}else if (NULL == Q.front->next->p->lchild){Q.front->next->p->rchild = pnew;//把新结点放到要插入结点的右边DeQueue(Q);//左右都放了结点后,辅助队列该删除第一个节点了//该函数只用于出队,不保存出队结点的数据}}}return 0;
}二叉树的遍历:
①前序遍历
首先前序遍历是先打印自身,再打印左子树,再打印右子树,我们通 过 PreOrder 函数来实现
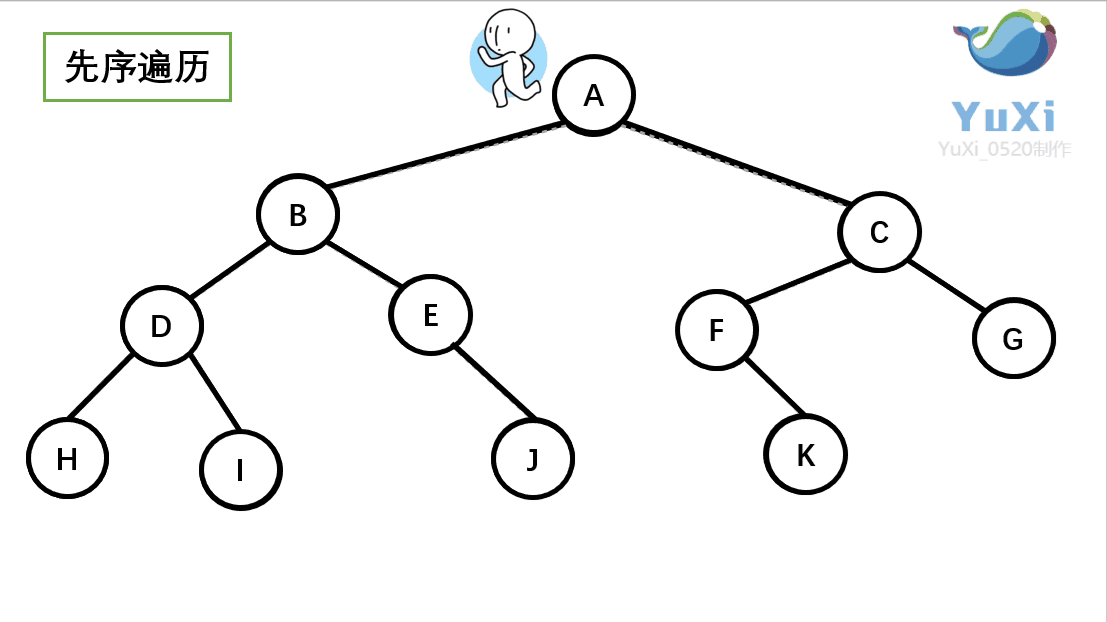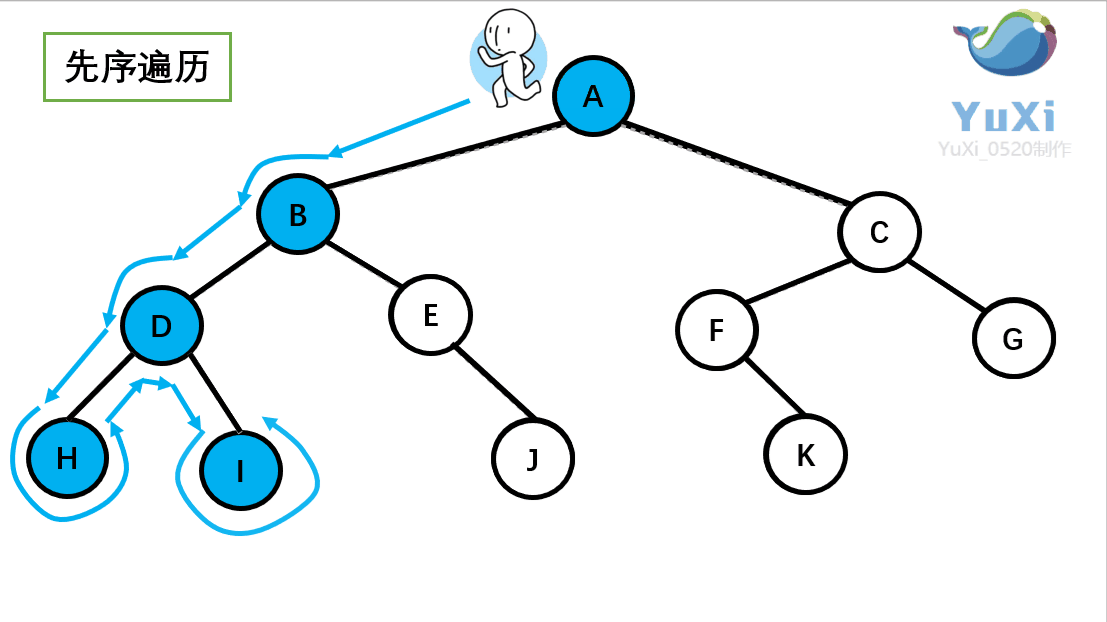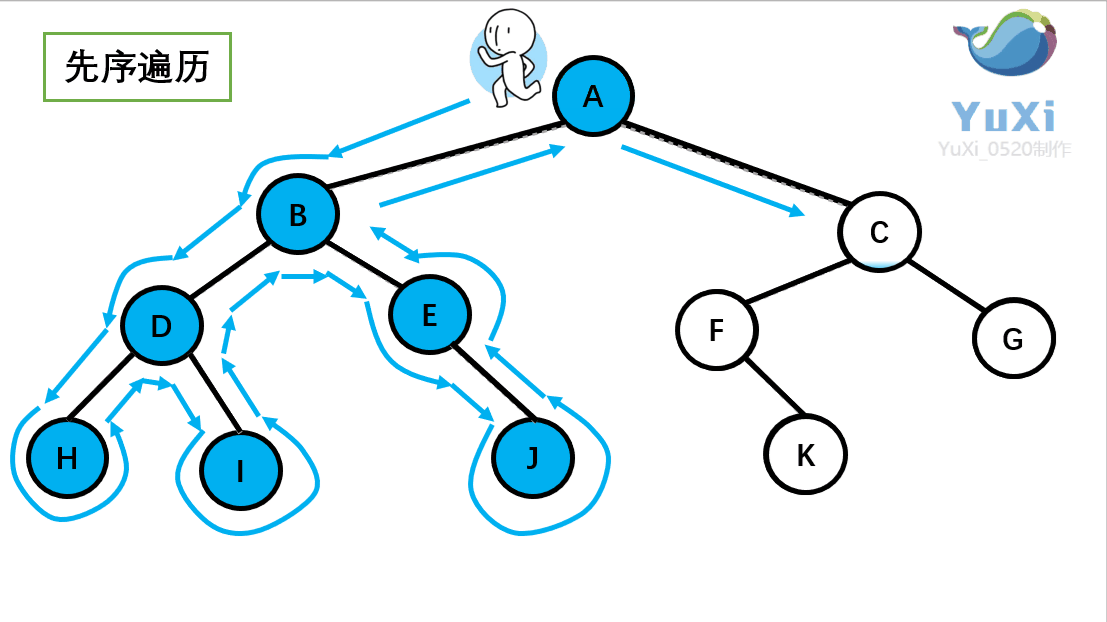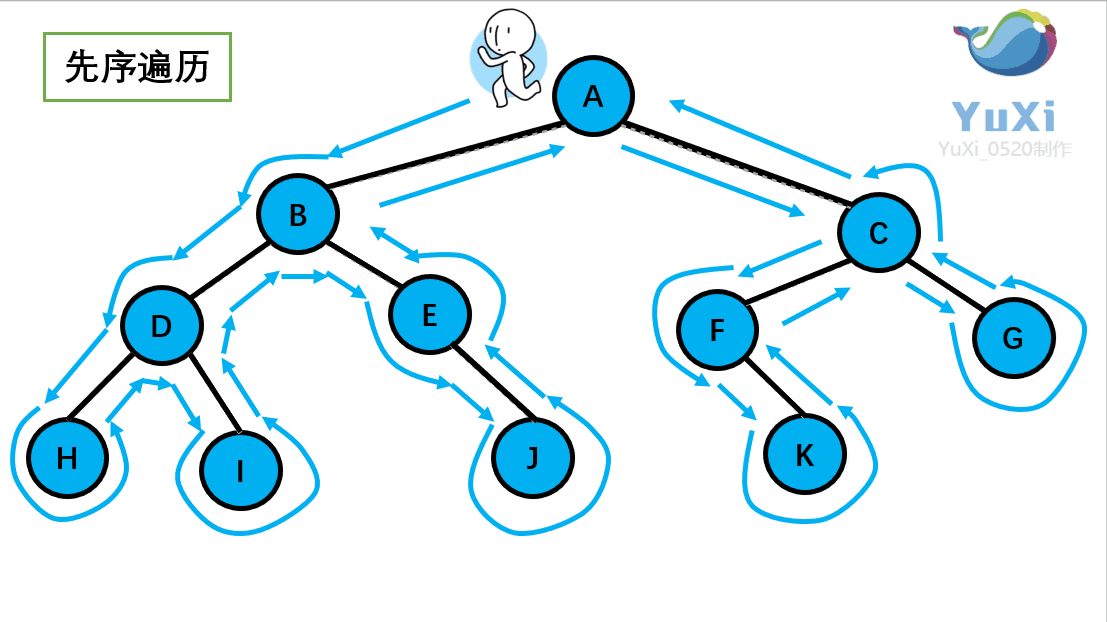
//递归实现
//abdhiejcfg 前序遍历,前序遍历就是深度优先遍历
void PreOrder(BiTree p)
{if (p != NULL){putchar(p->data);PreOrder(p->lchild);PreOrder(p->rchild);}
}②中序遍历
中序遍历是先打印左子树,再打印当前结点,再打印右子树,我 们通过 InOrder 函数来实现。
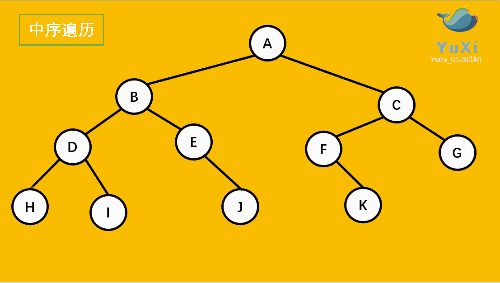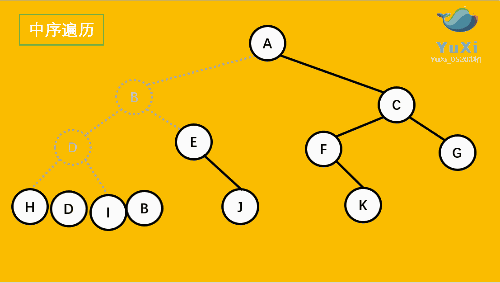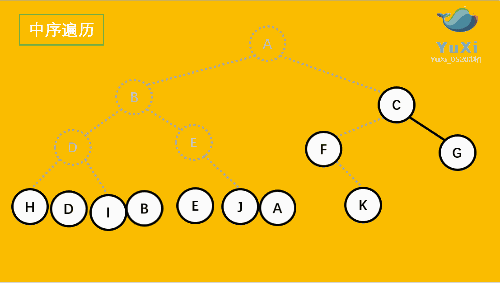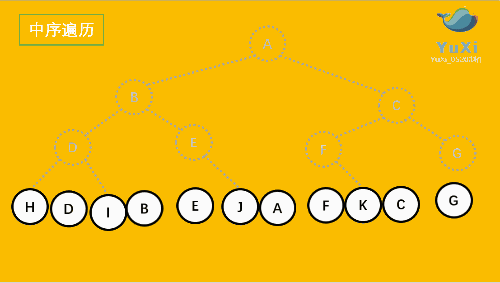
//中序遍历 hdibjeafcg
void InOrder(BiTree p)
{if (p != NULL){InOrder(p->lchild);putchar(p->data);InOrder(p->rchild);}
}③后序遍历
后序遍历是先打印左子树,再打印右子树,最后打印当前结点, 我们通过 PostOrder 函数来实现。
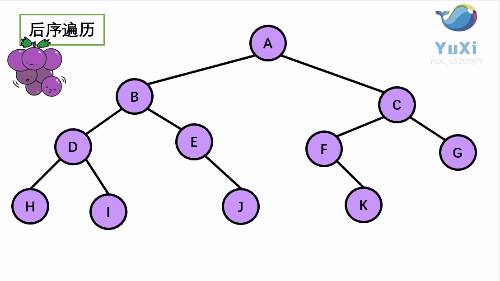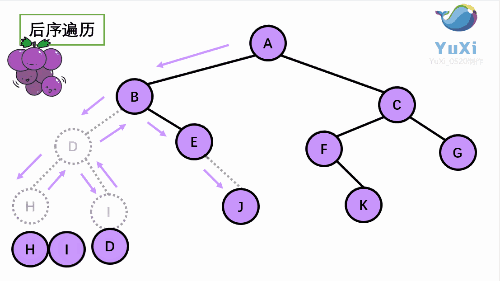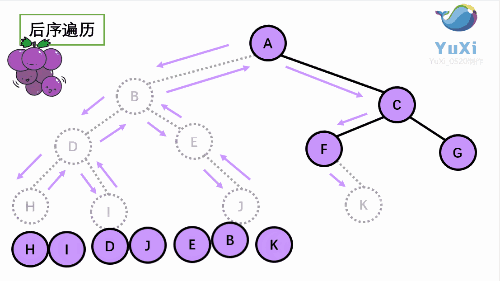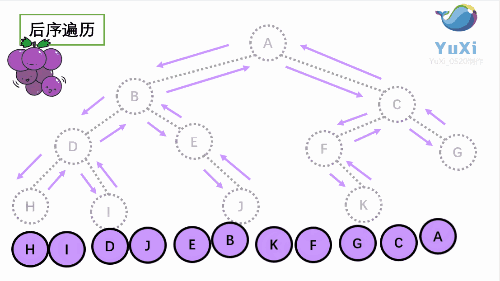
//hidjebfgca 后序遍历
void PostOrder(BiTree p)
{if (p != NULL){PostOrder(p->lchild);PostOrder(p->rchild);putchar(p->data);}
}④层次遍历
二叉树的层次遍历 ,顾名思义就是指从二叉树的第一层(根节点)开始,从上至下逐层遍历,在同一层中,则按照从左到右的顺序对节点逐个访问。在逐层遍历过程中,按从顶层到底层的次序访问树中元素,在同一层中,从左到右进行访问。
树根的地址作为辅助队列的第一个结点的数据域,然后删除第一个结点,保留数据域,然后借助树根的地址让自己的左孩子(b)和右孩子(c)分别入队,然后打印左孩子数据域(b),再入队左孩子的两个分支(de),然后打印右孩子的数据域,入队右孩子的两个分支(fg),然后一直这样循环。就可以把树连根拔起。
void LevelOrder(BiTree T)
{LinkQueue Q1;//辅助队列InitQueue(Q1);//初始化队列BiTree p;//存储出队的结点EnQueue(Q1, T);//树根入队while (!IsEmpty(Q1))//!是逻辑反操作{//队列不是空,循环继续DeQueue(Q1,p);//出队当前结点//p是出队结点的数据域,借助它找到出队结点指向的树的结点的左右孩子putchar(p->data);//打印数据域if (p->lchild != NULL) //入队左孩子{EnQueue(Q1, p->lchild);}if (p->rchild != NULL) //入队右孩子{EnQueue(Q1, p->rchild);}}
汇总:
#include <stdio.h>
#include <stdlib.h>
typedef char BiElemType;
typedef struct BiTNode{BiElemType data;struct BiTNode *lchild;struct BiTNode *rchild;
}BiTNode, *BiTree;
typedef struct LinkNode//LinkNode结构体是辅助队列的结点
{BiTree p;//树的某一个结点的地址值,不是数值struct LinkNode *next;//辅助队列中下一个结点
}LinkNode;
typedef struct //结构体,用于存放辅助队列头结点和队列尾结点的指针
{ LinkNode* front, *rear;
}LinkQueue;
void InitQueue(LinkQueue &Q) //初始化头尾指针,就是创建头结点,然后头尾指针都指向这一头结点
{Q.front = Q.rear = (LinkNode*)malloc(sizeof(LinkNode));//为辅助队列头结点申请空间//初始化时头尾指针都指向这一头结点Q.front->next = NULL;//头结点的next指针为NULL
}
bool IsEmpty(LinkQueue Q)
{if (Q.front == Q.rear)return true;elsereturn false;
}
void EnQueue(LinkQueue&Q, BiTree x)//入队,尾部插入法
{LinkNode *s = (LinkNode *)malloc(sizeof(LinkNode));//为入队的元素申请空间s->p = x; s->next = NULL;//新申请的结点作为最后一个结点Q.rear->next =s;//先让前一结点(Q.rear)的指针域指向新插入的结点Q.rear = s;//然后再让Q.rear变为指向尾部的那个结点
}
//出队 头部删除法
bool DeQueueF(LinkQueue &Q)
{//不保存删除结点数据域//front始终指向头结点,但头结点什么都没存LinkNode *q = Q.front->next;//将第一个节点存入qQ.front->next = q->next;//断链,保留第一个结点的指针域,让头节点指向第二个结点free(q);return true;
}
bool DeQueue(LinkQueue &Q, BiTree &x)//出队
{//x用于保存删除结点的数据域if (Q.front == Q.rear){return false;}//队列为空//front始终指向头结点,但头结点什么都没存LinkNode *q = Q.front->next;//将第一个节点存入qx = q->p;//获取要出队结点存储的值Q.front->next = q->next;//断链,保留第一个结点的指针域,让头节点指向第二个结点if (Q.rear == q)//删除的是最后一个元素{Q.rear = Q.front;//队列置为空}free(q);return true;
}
// 递归实现
//abdhiejcfg 前序遍历,前序遍历就是深度优先遍历
void PreOrder(BiTree p)
{if (p != NULL){putchar(p->data);PreOrder(p->lchild);PreOrder(p->rchild);}
}
//中序遍历 hdibjeafcg
void InOrder(BiTree p)
{if (p != NULL){InOrder(p->lchild);putchar(p->data);InOrder(p->rchild);}
}
//hidjebfgca 后序遍历
void PostOrder(BiTree p)
{if (p != NULL){PostOrder(p->lchild);PostOrder(p->rchild);putchar(p->data);}
}
void LevelOrder(BiTree T)
{LinkQueue Q1;//辅助队列InitQueue(Q1);//初始化队列BiTree p;//存储出队的结点EnQueue(Q1, T);//树根入队while (!IsEmpty(Q1))//!是逻辑反操作{//队列不是空,循环继续DeQueue(Q1,p);//出队当前结点//p是出队结点的数据域,借助它找到出队结点指向的树的结点的左右孩子putchar(p->data);//打印数据域if (p->lchild != NULL) //入队左孩子{EnQueue(Q1, p->lchild);}if (p->rchild != NULL) //入队右孩子{EnQueue(Q1, p->rchild);}}
int main()//二叉树的建树(层次建树)
{LinkQueue Q;//创建辅助队列头尾指针InitQueue(Q);//初始化头尾指针BiTree pnew;//用来指向新申请的树结点的指针BiTree tree = NULL;//树根的指针BiTree de;//char c;//输入内容为 abcdefghijwhile (scanf("%c", &c)){if (c == '\n'){break;}pnew = (BiTree)calloc(1, sizeof(BiTNode));//calloc申请空间并对空间进行初始化,赋值为0pnew->data = c;//数据放进去EnQueue(Q, pnew);//将新创建的树的结点的地址入队辅助队列//下面是建树的过程if (NULL == tree)//空树{tree = pnew; //tree指向树的根节点continue;//该节点为树的第一个节点//直接跳到循环的判断部分}else {if (NULL == Q.front->next->p->lchild)//如何把新结点放入树{//Q.front->next为辅助队列第一个结点Q.front->next->p->lchild = pnew;//把新结点放到要插入结点的左边}else if (NULL == Q.front->next->p->rchild){Q.front->next->p->rchild = pnew;//把新结点放到要插入结点的右边DeQueueF(Q);//左右都放了结点后,辅助队列该删除第一个节点了//该函数只用于出队,不保存出队结点的数据}}}printf("--------前序遍历----------\n");//也叫先序遍历,先打印当前结点,打印左孩子,打印右孩子PreOrder(tree);printf("\n--------中序遍历------------\n");//先打印左孩子,打印父亲,打印右孩子InOrder(tree);printf("\n--------后序遍历------------\n");//先打印左孩子,打印右孩子,最后打印父亲PostOrder(tree);printf("\n--------层次遍历-----------\n");LevelOrder(tree);printf("\n");return 0;
}效果:

希望这篇文章📃能对你有所帮助😁😁

相关文章:

数据结构 | 树 | 二叉树
🔥Go for it!🔥 📝个人主页:按键难防 📫 如果文章知识点有错误的地方,请指正!和大家一起学习,一起进步👀 📖系列专栏:数据结构与算法 ὒ…...

笔记:使用 unbuild 搭建 JavaScript 构建系统笔记
使用 unbuild 搭建 JavaScript 构建系统jcLee95:https://blog.csdn.net/qq_28550263?spm1001.2101.3001.5343 邮箱 :291148484163.com 简介: 本文是笔者阅读分析 elementPlus 项目时记录的。该项目用到了一个完全没有文档和资料的工具 unbu…...
【SpringBoot3.0源码】启动流程源码解析 •下
文章目录初始化DefaultBootstrapContext开启Headless模式获取监听器并启动封装命令行参数准备环境打印Banner创建上下文容器预初始化上下文容器刷新Spring容器打印启动时间发布事件执行特定的run方法上一篇《【SpringBoot3.0源码】启动流程源码解析 • 上》,主要讲解…...
QT(56)-动态链接库-windows-导出变量-导出类
1.导出变量 1.1不使用_declspec(dllimport) _declspec(dllexport) 使用_declspec(dllimport) _declspec(dllexport) 1.2win32 mydllwin32 myexe 1.3win32 mydllqt myexe 2.导出类 使用_declspec(dllimport) _declspec(dllexport) 2.1不用关键…...
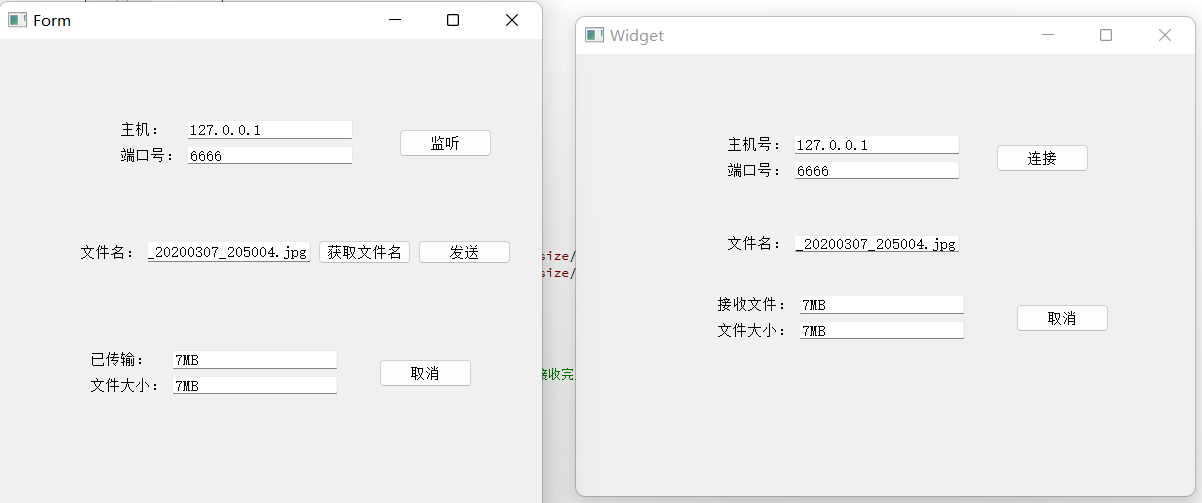
TCP传输文件
传输文件和传输信息的区别: 传输信息,只是一条数据,传输文件是多条数据传输信息传输过去一般都会显示,传输文件一般不会显示,一般只是存放在文件中传输文件需要传输,文件大小和文件名称(不然不知…...
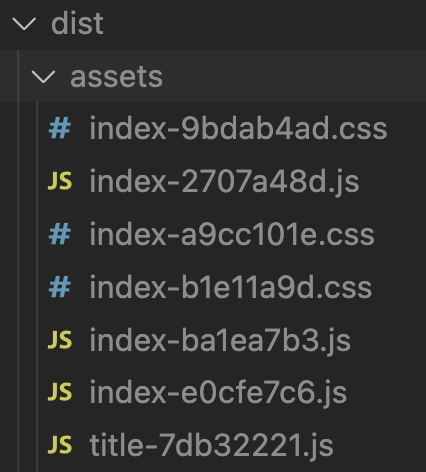
vue3:加载本地图片等静态资源
背景 在我们用 vue2 webpack 的时候,加载图片资源是这样用的: <img :src"require(/assets/test.png)" />这样打包后就会触发 file-loader 打包图片资源,在 dist 文件夹中就可以看到这个图片(如果图片较小会打包…...

工作记录------数据库group_concat函数长度问题
工作记录------group_concat函数长度问题 背景:页面在数据展示时,报错,错误显示:String index out of range: -1 异常信息 java.lang.StringIndexOutOfBoundsException: String index out of range: -1at java.lang.String.sub…...
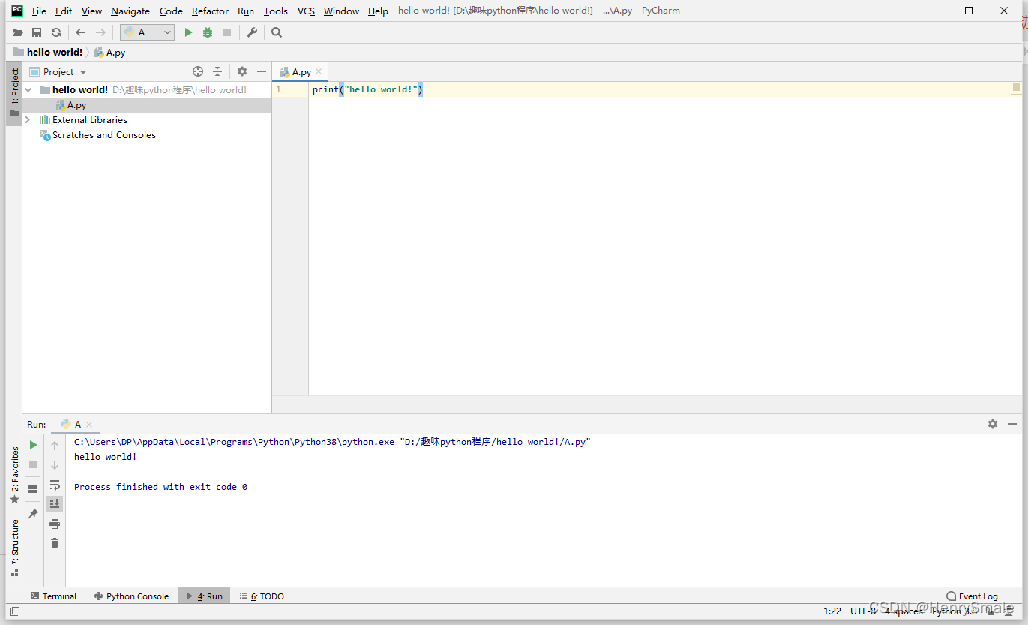
Python基础语法
1 编程环境 1.1 编译环境 pycharmpython/anaconda 1.2 环境设置 File -> settings -> Project interpreter -> 1.3 Hello world 2 条件判断 2.1 例题 【题1】输入一个年份,判断是否是闰年 ①能被4整除,但不能被100整除; ②能被400整…...
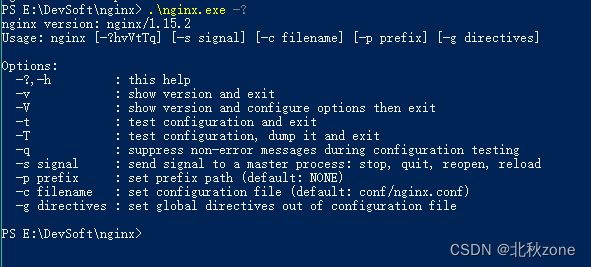
windows环境下安装Nginx及常用操作命令
windows环境下安装Nginx及常用操作命令nginx基本概述基本用途nginx安装nginx基本概述 Nginx (engine x) 是一个高性能的HTTP和反向代理web服务器。基本用途 nginx是一个轻量级高并发服务器,而tomcat并不是。nginx一般被用来做反向代理,将请求转发到应用…...

python excel数据处理?
前段时间做了个小项目,帮个海洋系的教授做了个数据处理的软件。基本的功能很简单,就是对Excel里面的一些数据进行过滤,统计,对多个表的内容进行合并等。之前没有处理Excel数据的经验,甚至于自己都很少用到Excel。记得《…...
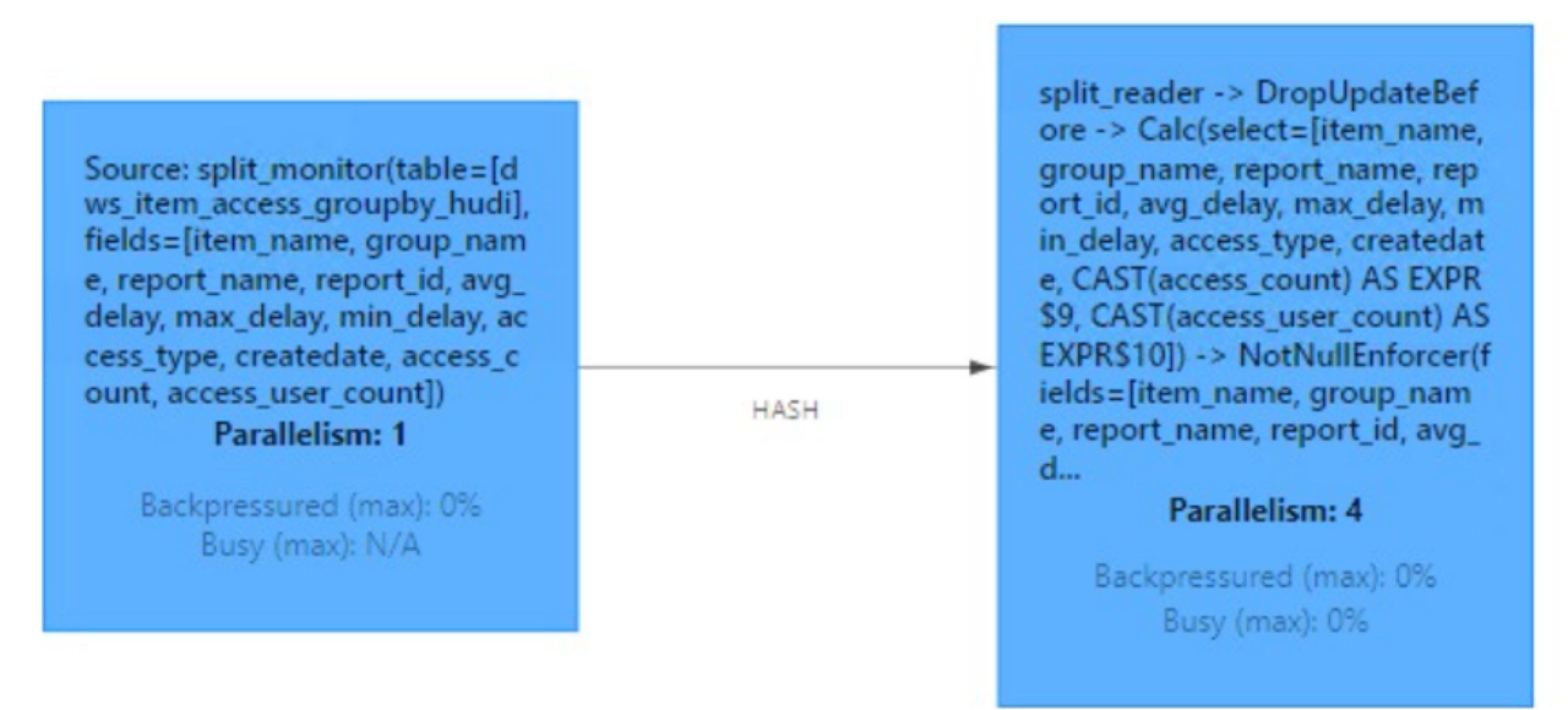
Hudi-集成Flink
文章目录集成Flink环境准备sql-client方式启动sql-client插入数据查询数据更新数据流式插入code 方式环境准备代码类型映射核心参数设置去重参数并发参数压缩参数文件大小Hadoop参数内存优化读取方式流读(Streaming Query)增量读取(Increment…...
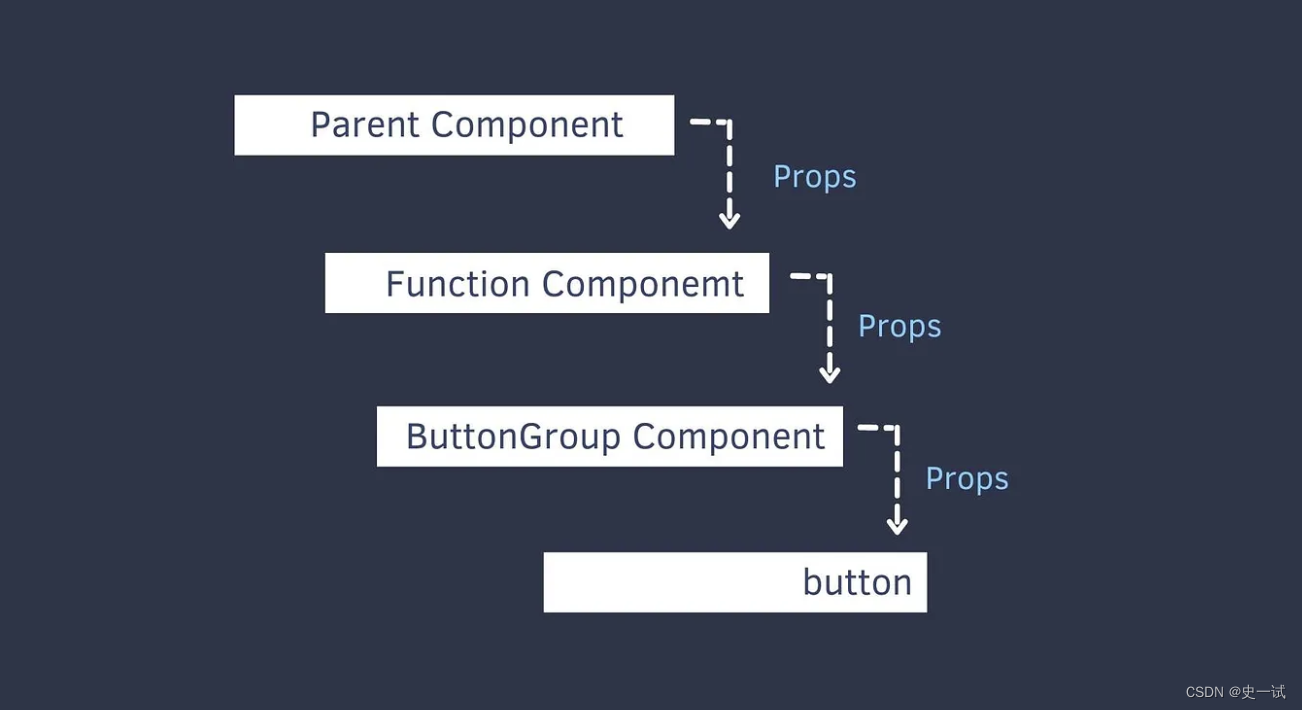
重新认识 React Hooks useContext
通常来说,React 数据的传递方式都是一层一层把资料 props 传到子层的 就算第二层(Function Component)、第三层(Button Group Compontn) 根本没有用到这个资料,但是为了传到最底层(button) ,每一层还是必须要传props // App.js const App = () => {const [dark, setDark…...
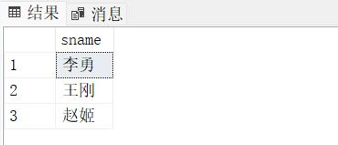
数据库(2)--加深对统计查询的理解,熟练使用聚合函数
一、内容要求 利用sql建立学生信息数据库,并定义以下基本表: 学生(学号,年龄,性别,系号) 课程(课号,课名,学分,学时) 选课࿰…...
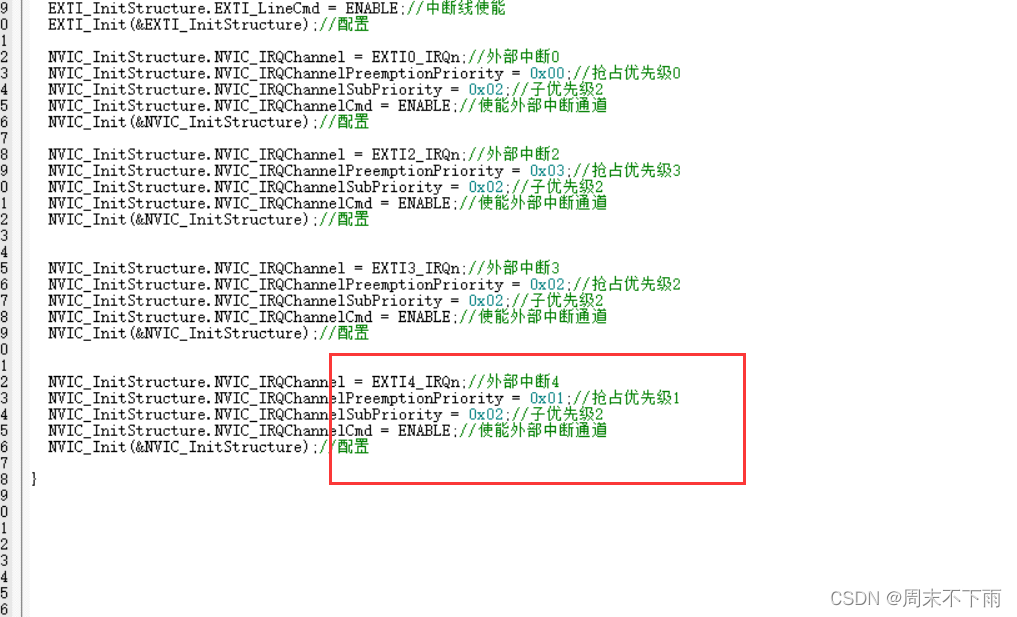
stm32f407探索者开发板(十五)——NVIC中断优先级管理
文章目录零、前言一、NVIC中断优先级分组1.1 中断的管理方法1.2 抢占优先级&相应优先级的区别1.3 举例1.4 特别说明1.5 中断优先级分组函数二、NVIC中断优先级设置2.1 中断设置相关寄存器2.2 中断设置优先级2.2.1 中断优先级控制的寄存器组 IP[240]2.2.2 中断使能寄存器组 …...
【Azure 架构师学习笔记】-Azure Logic Apps(6)- Logic Apps调用ADF
本文属于【Azure 架构师学习笔记】系列。 本文属于【Azure Logic Apps】系列。 接上文【Azure 架构师学习笔记】-Azure Logic Apps(5)- 标准和使用量类型的区别 前言 Logic Apps 和 ADF 的搭配使用是常见的组合,它们可以互相弥补各自的不足和…...

python随机获取列表中某一元素
1、利用Python中的random模块中的choice方法 random.choice()可以从任何序列,比如list列表中,选取一个随机的元素返回,可以用于字符串、列表、元组等。 import random arr[1,2,3,4,5,6] print(random.choice(arr))2、利用Python中的random模…...

Nacos微服务笔记
Nacos安装Nacos 的 Github(Tags alibaba/nacos GitHub)下载我们所需的 Nacos 版本,可以选择 windows 或者 Linux。 进入官网,选择合适版本,tar.gz为linux版本,zip为windows版本。下载并解压 nacos-server…...
MAC文件误删怎么办?mac数据恢复,亲测很好用的方法
电脑文件误删,应该很多人都经历过。之前分享了很多关于Windows电脑文件误删如何恢复的方法,那么MAC电脑文件误删该怎么办?有什么好方法可以使得mac数据恢复回来吗?下面就给大家分享一些亲测好用的方法! 一、MAC电脑的文…...

机械革命z2黑苹果改造计划第二番-MacOS实用软件渗透工具
机械革命z2黑苹果改造计划第二番-实用软件 Mac实用工具 这是旧电脑改造计划的第二篇,就是安装一些常用软件和一些渗透测试工具,武装灵魂成为真正的生产力工具 首先推荐一个网站,www.mactools.app,这个软件里边有大多数常用的软…...
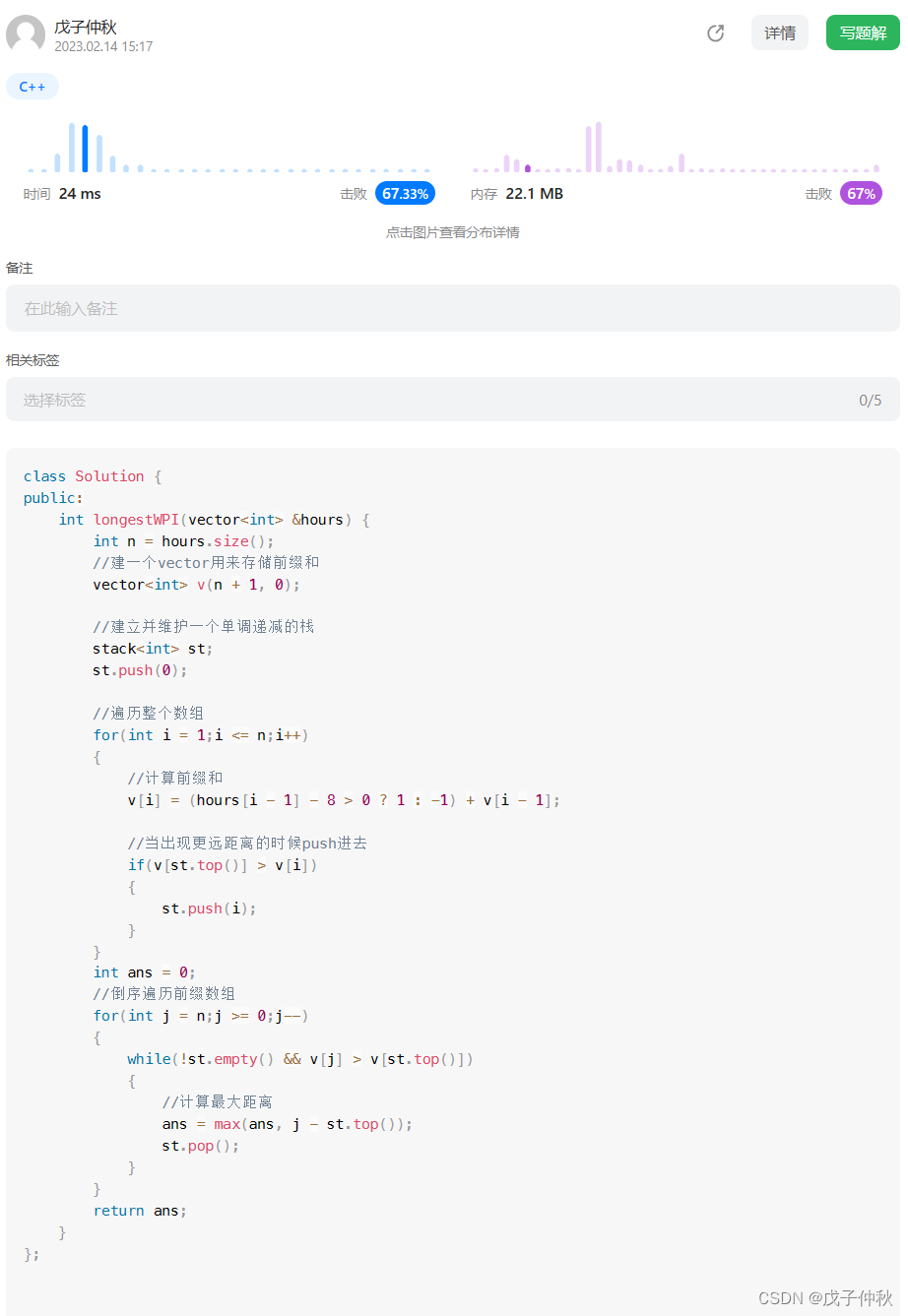
【LeetCode】每日一题(4)
目录 题目:1124. 表现良好的最长时间段 - 力扣(Leetcode) 题目的接口: 解题思路: 代码: 过啦!!! 写在最后: 题目:1124. 表现良好的最长时间…...

ubuntu搭建nfs服务centos挂载访问
在Ubuntu上设置NFS服务器 在Ubuntu上,你可以使用apt包管理器来安装NFS服务器。打开终端并运行: sudo apt update sudo apt install nfs-kernel-server创建共享目录 创建一个目录用于共享,例如/shared: sudo mkdir /shared sud…...

PHP和Node.js哪个更爽?
先说结论,rust完胜。 php:laravel,swoole,webman,最开始在苏宁的时候写了几年php,当时觉得php真的是世界上最好的语言,因为当初活在舒适圈里,不愿意跳出来,就好比当初活在…...

QMC5883L的驱动
简介 本篇文章的代码已经上传到了github上面,开源代码 作为一个电子罗盘模块,我们可以通过I2C从中获取偏航角yaw,相对于六轴陀螺仪的yaw,qmc5883l几乎不会零飘并且成本较低。 参考资料 QMC5883L磁场传感器驱动 QMC5883L磁力计…...

【android bluetooth 框架分析 04】【bt-framework 层详解 1】【BluetoothProperties介绍】
1. BluetoothProperties介绍 libsysprop/srcs/android/sysprop/BluetoothProperties.sysprop BluetoothProperties.sysprop 是 Android AOSP 中的一种 系统属性定义文件(System Property Definition File),用于声明和管理 Bluetooth 模块相…...

【C语言练习】080. 使用C语言实现简单的数据库操作
080. 使用C语言实现简单的数据库操作 080. 使用C语言实现简单的数据库操作使用原生APIODBC接口第三方库ORM框架文件模拟1. 安装SQLite2. 示例代码:使用SQLite创建数据库、表和插入数据3. 编译和运行4. 示例运行输出:5. 注意事项6. 总结080. 使用C语言实现简单的数据库操作 在…...

涂鸦T5AI手搓语音、emoji、otto机器人从入门到实战
“🤖手搓TuyaAI语音指令 😍秒变表情包大师,让萌系Otto机器人🔥玩出智能新花样!开整!” 🤖 Otto机器人 → 直接点明主体 手搓TuyaAI语音 → 强调 自主编程/自定义 语音控制(TuyaAI…...

k8s业务程序联调工具-KtConnect
概述 原理 工具作用是建立了一个从本地到集群的单向VPN,根据VPN原理,打通两个内网必然需要借助一个公共中继节点,ktconnect工具巧妙的利用k8s原生的portforward能力,简化了建立连接的过程,apiserver间接起到了中继节…...

Android Bitmap治理全解析:从加载优化到泄漏防控的全生命周期管理
引言 Bitmap(位图)是Android应用内存占用的“头号杀手”。一张1080P(1920x1080)的图片以ARGB_8888格式加载时,内存占用高达8MB(192010804字节)。据统计,超过60%的应用OOM崩溃与Bitm…...

HashMap中的put方法执行流程(流程图)
1 put操作整体流程 HashMap 的 put 操作是其最核心的功能之一。在 JDK 1.8 及以后版本中,其主要逻辑封装在 putVal 这个内部方法中。整个过程大致如下: 初始判断与哈希计算: 首先,putVal 方法会检查当前的 table(也就…...

基于Java Swing的电子通讯录设计与实现:附系统托盘功能代码详解
JAVASQL电子通讯录带系统托盘 一、系统概述 本电子通讯录系统采用Java Swing开发桌面应用,结合SQLite数据库实现联系人管理功能,并集成系统托盘功能提升用户体验。系统支持联系人的增删改查、分组管理、搜索过滤等功能,同时可以最小化到系统…...
