哈夫曼树【北邮机试】
一、哈夫曼树
机试考察的最多的就是WPL,是围绕其变式展开考察。

哈夫曼树的构建是不断选取集合中最小的两个根节点进行合并,而且在合并过程中排序也会发生变化,因此最好使用优先队列来维护单调性,方便排序和合并。
核心代码如下:
//取出两个权最小的
int num1 = (q.top()).x;
q.pop();
int num2 = (q.top()).x;
q.pop();
//权相加,生成新的节点,并放入队列
node new_node;
new_node.x = num1 + num2;
q.push(new_node);
//结果累加。本来树的带权路径计算是所有节点深度*权的和,但是这里通过
//几层累加,也能实现乘法的效果。在最下面的节点,累加次数最多,即相当于
//乘的数值最大
ans += num1 + num2;
//输出的ans即为最终WPL的值
二、哈夫曼树(北邮机试)
Time Limit: 1000 ms
Memory Limit: 256 mb
哈夫曼树,第一行输入一个数n,表示叶结点的个数。需要用这些叶结点生成哈夫曼树,根据哈夫曼树的概念,这些结点有权值,即weight,题目需要输出所有结点的值与权值的乘积之和。
输入输出格式:
输入格式
输入有多组数据。
每组第一行输入一个数n,接着输入n个叶节点(叶节点权值不超过100,2<=n<=1000)。
输出格式
输出权值。
输入输出样例:
输入样例:
5
1 2 2 5 9
输出样例:
37
AC代码如下:
#include<bits/stdc++.h>
using namespace std;struct Node {int x;Node(int a) {x = a;}//定义一下构造函数
};//重新定义比较运算符
bool operator < (const Node& a, const Node& b) {return a.x>b.x;
}//计算WPL
int getWPL(priority_queue<Node> q) {int sum = 0;while(q.size()>1) {//只剩下根节点的时候退出 int num1 = (q.top()).x;q.pop();int num2 = (q.top()).x;q.pop();Node tmp(num1+num2);q.push(tmp);sum += num1+num2; }return sum;
}int main() {int n;while(cin>>n){int a[n];priority_queue<Node> q;for(int i=0 ; i<n ; i++) {cin>>a[i];Node tmp(a[i]);q.push(tmp);}int sum = getWPL(q);cout<<sum<<endl; }return 0;
}
三、哈夫曼编码
输入输出格式:
输入格式
输入文件将包含文本字符串列表,每行一个。 文本字符串将仅包含大写字母数字字符和下划线(用于代替空格)。 输入结束将通过仅包含单词“ END”作为文本字符串的行来表示。 此行不应被处理。
输出格式
对于输入中的每个文本字符串,输出8位ASCII编码的位长度,最佳无前缀可变长度编码的位长度以及精确到小数点后的压缩率。
输入输出样例:
输入样例:
AAAAABCD
THE_CAT_IN_THE_HAT
END
输出样例:
64 13 4.9
144 51 2.8
分析:这道题目关键在于计算压缩后的长度,本质上也是计算WPL(这里的权值是每个字母出现的次数,路径长度就是编码的长度,一个二进制数就是一位)。
AC代码如下:
#include<bits/stdc++.h>
using namespace std;string str;
int len, num[30];int bfs() {priority_queue<int, vector<int>, greater<int> > q; // 创建优先队列,从小到大排序for(int i = 0; i < 30; i++) {if(num[i]) q.push(num[i]); // 放入每个字母的个数}int sum = 0;if(q.size() == 1) sum = q.top(); // 如果只有一个字母,直接等于该字母的数量while(q.size() > 1) { // 得到前两个最小的叶子节点,将和放入队列中int a = q.top(); q.pop();int b = q.top(); q.pop();sum += (a + b); q.push(a + b); // 因为ans累加了之前的值,所以传入的是a + b而非ans;}return sum;
}int main() {while(cin >> str) {memset(num, 0, sizeof num);if(str == "END") break; // 注意为双引号len = str.size(); // 得到string类型的长度for(int i = 0; i < len; i++) {if(str[i] == '_') num[26]++; // 应为'A' - 'A'等于0,从下标0开始,所以'_'就在num[26]else num[str[i] - 'A']++;} int res = bfs();printf("%d %d %.1lf\n", len * 8, res, len * 8.0 / res);}return 0;
}
四、合并果子(中南大学机试)
Time Limit: 1000 ms
Memory Limit: 256 mb
在一个果园里,多多已经将所有的果子打了下来,而且按果子的不同种类分成了不同的堆。多多决定把所有的果子合成一堆。 每一次合并,多多可以把两堆果子合并到一起,消耗的体力等于两堆果子的重量之和。可以看出,所有的果子经过n-1次合并之后,就只剩下一堆了。多多在合并果子时总共消耗的体力等于每次合并所耗体力之和。 因为还要花大力气把这些果子搬回家,所以多多在合并果子时要尽可能地节省体力。假定每个果子重量都为1,并且已知果子的种类数和每种果子的数目,你的任务是设计出合并的次序方案,使多多耗费的体力最少,并输出这个最小的体力耗费值。 例如有3种果子,数目依次为1,2,9。可以先将1、2堆合并,新堆数目为3,耗费体力为3。接着,将新堆与原先的第三堆合并,又得到新的堆,数目为12,耗费体力为12。所以多多总共耗费体力=3+12=15。可以证明15为最小的体力耗费值。
输入输出格式:
输入格式
输入包括两行,第一行是一个整数n(1<=n<=10000),表示果子的种类数。第二行包含n个整数,用空格分隔,第i个整数ai(1<=ai<=20000)是第i种果子的数目。
输出格式
输出包括一行,这一行只包含一个整数,也就是最小的体力耗费值。输入数据保证这个值小于2^31。
输入输出样例:
输入样例:
3
1 2 9
输出样例:
15
分析:这题本质上还是计算WPL,只是题面比较明显看出在构造哈夫曼树过程中对权值进行累加。
AC代码直接参考【北邮机试】代码,输出ans即可。
相关文章:

哈夫曼树【北邮机试】
一、哈夫曼树 机试考察的最多的就是WPL,是围绕其变式展开考察。 哈夫曼树的构建是不断选取集合中最小的两个根节点进行合并,而且在合并过程中排序也会发生变化,因此最好使用优先队列来维护单调性,方便排序和合并。 核心代码如下…...
thinkphp:数值(保留小数点后N位,四舍五入,左侧补零,格式化货币,取整,生成随机数,数字与字母进行转换)
一、保留小数点后N位/类似四舍五入(以保留小数点后三位为准) number_format()函数:第一个参数为要格式化的数字,第二个参数为保留的小数位数 方法一: public function test() {$num 12.56789; // 待格式化的数字$r…...

用Flutter你得了解的七个问题
Flutter是Google推出的一款用于构建高性能、高保真度移动应用程序、Web和桌面应用程序的开源UI工具包。Flutter使用自己的渲染引擎绘制UI,为用户提供更快的性能和更好的体验。 Flutter使用Dart语言,具有强大的类型、效率和易学能力,基本上你…...

Nmap使用手册
Nmap语法 -A 全面扫描/综合扫描 nmap-A 127.0.0.1 扫描指定网段 nmap 127.0.0.1 nmap 127.0.0.1/24Nmap 主机发现 -sP ping扫描 nmap -sP 127.0.0.1-P0 无ping扫描备注:【协议1,协设2〕【目标】扫描 nmap -P0 127.0.0.1如果想知道是如何判断目标主机是否存在可…...
基于ResNet-attention的负荷预测
一、attention机制 注意力模型最近几年在深度学习各个领域被广泛使用,无论是图像处理、语音识别还是自然语言处理的各种不同类型的任务中,都很容易遇到注意力模型的身影。从注意力模型的命名方式看,很明显其借鉴了人类的注意力机制。我们来看…...
)
华为校招机试 - 批量初始化次数(20230426)
题目描述 某部门在开发一个代码分析工具,需要分析模块之间的依赖关系,用来确定模块的初始化顺序是否有循环依赖等问题。 "批量初始化”是指一次可以初始化一个或多个模块。 例如模块1依赖模块2,模块3也依赖模块2,但模块1和3没有依赖关系,则必须先"批量初始化”…...
WhatsApp CRM:通过 CRM WhatsApp 集成向客户发送消息
WhatsApp CRM:通过 CRM WhatsApp 集成向客户发送消息 你是否在寻找一个支持WhatsApp整合的CRM?或者,你想将WhatsApp与你当前的CRM整合?这篇文章将回答你所有的问题。我们将首先了解什么是WhatsApp CRM,以及你需要知道…...
SOLIDWORKS Electrical无缝集成电气和机械设计
集成电气系统设计SOLIDWORKS⑧Electrical 解决方案借助专为工程专业设计的特定工具简化了电气铲品设计,并借助直观的用户界面更快地设计嵌入式电气系统。 与SOLIDWORKS 3DCAD的原生集成能提供更好的协作与生产效率,同时减少产品延迟、提高设计的一致性与…...

Numpy从入门到精通——数组变形|合并数组
这个专栏名为《Numpy从入门到精通》,顾名思义,是记录自己学习numpy的学习过程,也方便自己之后复盘!为深度学习的进一步学习奠定基础!希望能给大家带来帮助,爱睡觉的咋祝您生活愉快! 这一篇介绍《…...
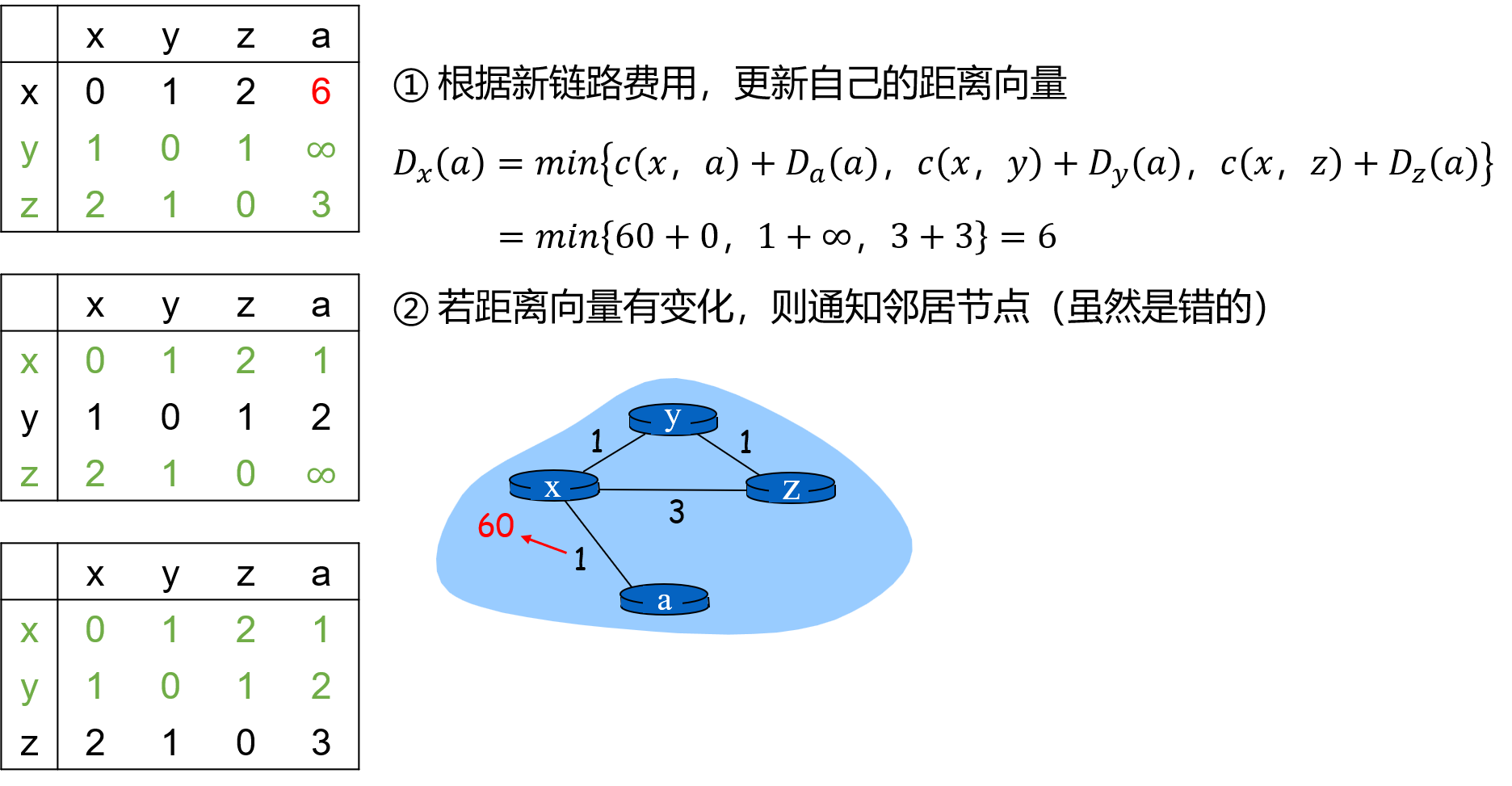
DJ4-5 路由算法:LS 和 DV
目录 一、迪杰斯特拉算法 1. 术语定义 2. 算法描述 3. 举例说明 4. 构建从源节点到目的节点的路径 5. 构建最低费用路径树 6. 构建转发表 二、距离向量路由算法 1. 术语定义 2. 举例说明 3. 距离向量表 4. 更新距离向量表 5. 举例说明 三、距离向量路由算法 PLUS…...

python图像处理之形态学梯度、礼帽、黑帽
文章目录 简介实战 简介 腐蚀和膨胀是图像形态学处理的基本运算,这两种运算的复合运算构成了开和闭,而腐蚀、膨胀与原图之间的加减操作,则构成了形态学梯度、礼帽和黑帽计算。 由于这几种函数均基于腐蚀和膨胀,所以其参数均与开…...
千万级直播系统后端架构设计
1、架构方面 1.1 基本 该图是某大型在线演唱会的直播媒体架构简图。 可以看出一场大型活动直播涵盖的技术方案点非常庞杂,本节接下来的内容我们将以推拉流链路、全局智能调度、流量精准调度以及单元化部署,对这套直播方案做一个展开介绍。 1.2 推拉流链…...
)
ImageJ 用户手册——第五部分(菜单命令File,Edit)
这里写目录标题 菜单命令26. File26.1 New26.1.1 Image26.1.2 Hyperstack26.1.3 Text Window26.1.4 Internal Clipboard26.1.5 System Clipboard 26.2 Open26.3 Open Next26.4 Open Samples26.5 Open Recent26.6 Import26.6.1 Image Sequence26.6.2 Raw26.6.3 LUT26.6.4 Text I…...

nmap常用命令
一、nmap简介 Nmap,也就是Network Mapper。nmap是一个网络连接端扫描软件,用来扫描网上电脑开放的网络连接端。确定哪些服务运行在哪些连接端,并且推断计算机运行哪个操作系统(这是亦称 fingerprinting)。它是网络管理员必用的软件之一&…...

常用adb 命令
目录 一、常用简单的adb命令: 二、adb shell pm基本的命令: 三、adb shell am基本的命令: 四、关闭某项进程,以monkey为例: 五、最近12小时的资源情况: 六、录制屏幕命令: 七、截图命令&am…...
)
后端开发常犯的问题(Java版)
数据类型使用不当 ——钱相关的计算,数据类型必须用BigDecimal 1.很多开发在做金额计算时会使用double数据类型,自测一些常用场景认为double是满足需求的因而图省事直接使用此数据类型。使用double类型存在金额精度丢失的风险,涉及到钱的数据…...

Vue CLI 部署
通用指南 如果你用 Vue CLI 处理静态资源并和后端框架一起作为部署的一部分,那么你需要的仅仅是确保 Vue CLI 生成的构建文件在正确的位置,并遵循后端框架的发布方式即可。 如果你独立于后端部署前端应用——也就是说后端暴露一个前端可访问的 API&…...

客快物流大数据项目(一百一十七):网关 Spring Cloud Gateway
文章目录 网关 Spring Cloud Gateway 一、简介 1、功能特性...
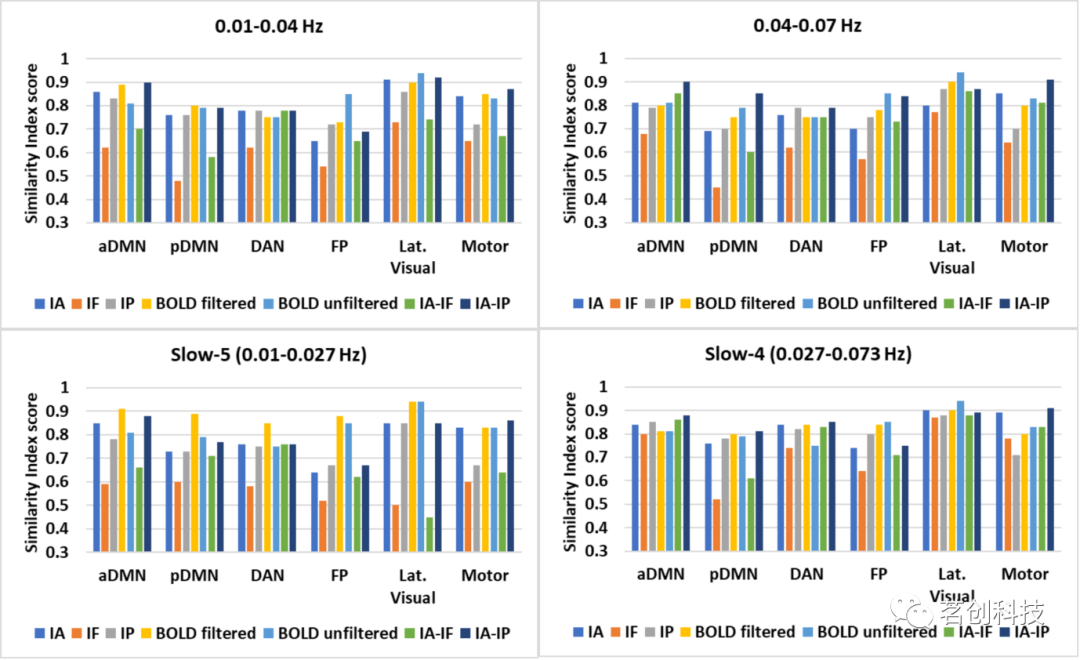
fMRI时间序列振幅和相位对功能连接分析的影响
导读 目的:fMRI领域的一些研究使用瞬时相位(IP)表征(源自BOLD时间序列的解析表征)考察了脑区之间的同步性。本研究假设来自不同脑区的瞬时振幅(IA)表征可以为脑功能网络提供额外的信息。为此,本研究探索了静息态BOLD fMRI信号的这种表征,用于…...

备战2个月,四轮面试拿下字节offer...
背景 菜 J 一枚,本硕都是计算机(普通二本),2021 届应届硕士,软件测试方向。个人也比较喜欢看书,技术书之类的都有看,最后下面也会推荐一些经典书籍。 先说一下春招结果:拿下了四个…...

19c补丁后oracle属主变化,导致不能识别磁盘组
补丁后服务器重启,数据库再次无法启动 ORA01017: invalid username/password; logon denied Oracle 19c 在打上 19.23 或以上补丁版本后,存在与用户组权限相关的问题。具体表现为,Oracle 实例的运行用户(oracle)和集…...

最新SpringBoot+SpringCloud+Nacos微服务框架分享
文章目录 前言一、服务规划二、架构核心1.cloud的pom2.gateway的异常handler3.gateway的filter4、admin的pom5、admin的登录核心 三、code-helper分享总结 前言 最近有个活蛮赶的,根据Excel列的需求预估的工时直接打骨折,不要问我为什么,主要…...

【ROS】Nav2源码之nav2_behavior_tree-行为树节点列表
1、行为树节点分类 在 Nav2(Navigation2)的行为树框架中,行为树节点插件按照功能分为 Action(动作节点)、Condition(条件节点)、Control(控制节点) 和 Decorator(装饰节点) 四类。 1.1 动作节点 Action 执行具体的机器人操作或任务,直接与硬件、传感器或外部系统…...

P3 QT项目----记事本(3.8)
3.8 记事本项目总结 项目源码 1.main.cpp #include "widget.h" #include <QApplication> int main(int argc, char *argv[]) {QApplication a(argc, argv);Widget w;w.show();return a.exec(); } 2.widget.cpp #include "widget.h" #include &q…...

vue3 定时器-定义全局方法 vue+ts
1.创建ts文件 路径:src/utils/timer.ts 完整代码: import { onUnmounted } from vuetype TimerCallback (...args: any[]) > voidexport function useGlobalTimer() {const timers: Map<number, NodeJS.Timeout> new Map()// 创建定时器con…...

laravel8+vue3.0+element-plus搭建方法
创建 laravel8 项目 composer create-project --prefer-dist laravel/laravel laravel8 8.* 安装 laravel/ui composer require laravel/ui 修改 package.json 文件 "devDependencies": {"vue/compiler-sfc": "^3.0.7","axios": …...

docker 部署发现spring.profiles.active 问题
报错: org.springframework.boot.context.config.InvalidConfigDataPropertyException: Property spring.profiles.active imported from location class path resource [application-test.yml] is invalid in a profile specific resource [origin: class path re…...

中医有效性探讨
文章目录 西医是如何发展到以生物化学为药理基础的现代医学?传统医学奠基期(远古 - 17 世纪)近代医学转型期(17 世纪 - 19 世纪末)现代医学成熟期(20世纪至今) 中医的源远流长和一脉相承远古至…...

三分算法与DeepSeek辅助证明是单峰函数
前置 单峰函数有唯一的最大值,最大值左侧的数值严格单调递增,最大值右侧的数值严格单调递减。 单谷函数有唯一的最小值,最小值左侧的数值严格单调递减,最小值右侧的数值严格单调递增。 三分的本质 三分和二分一样都是通过不断缩…...

uniapp 开发ios, xcode 提交app store connect 和 testflight内测
uniapp 中配置 配置manifest 文档:manifest.json 应用配置 | uni-app官网 hbuilderx中本地打包 下载IOS最新SDK 开发环境 | uni小程序SDK hbulderx 版本号:4.66 对应的sdk版本 4.66 两者必须一致 本地打包的资源导入到SDK 导入资源 | uni小程序SDK …...
