当前位置： 首页 > news >正文

【计算机图形学】课堂习题汇总

news 文章来源：https://blog.csdn.net/m0_65787507/article/details/130440299 2025/4/21 22:27:01

在直线的光栅化算法中，如果不考虑最大位移方向则可能得到怎样的直线？

A：斜率为1的线

B：总是垂直的

C：离散的点，无法构成直线

D：总是水平的

在直线的改进的Bresenham算法中，每当误差项k大于0.5以后必须让k减去1，否则此后的直线将变成怎样？

A：斜率绝对值为1的线

B：垂直的

C：水平的

D：离散的

椭圆弧的扫描转换算法中，如果考虑的是中心在原点，第一象限的1/4段椭圆弧，则上下部分的分界点是哪一个？

A：椭圆弧上切线斜率为1的点

B：椭圆弧上法向量x、y两个分量互为相反数的点

C：椭圆弧上切线斜率为-1的点

D：椭圆弧与直线y=x的交点

在直线的中点算法中，如果直线在第一象限，斜率k在0到1之间，如果当前点为p(x,y)，则其候选点为？

A：(x,y+1)

B：(x+1,y)

C：(x+1,y-1)

D：(x+1,y+1)

A点的代码为：

 

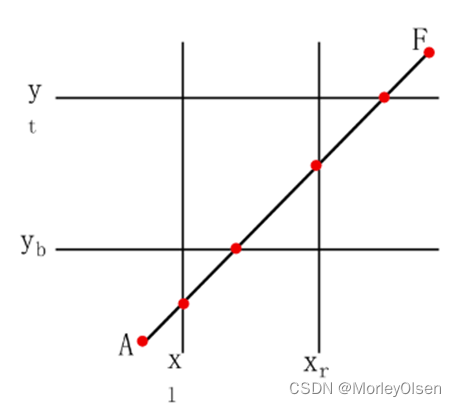
A：0000

B：1001

C：0101

D：0001

P1点的编码为0001，P2点的编码为0100，判断线段和窗口的关系。

A：完全在窗口内

B：完全在窗口外

C：和窗口相交

D：无法判断

 

Liang-Barsky算法中，若P1=P2=0，且q1<0，则该线段的位置为：

A：完全在窗口内部

B：和窗口相交

C：在窗口上边界外平行

D：在窗口左边界外平行

在多边形的逐边裁剪法中，对于某条多边形的边（方向为从端点S到端点P）与某条裁剪线（窗口的某一边）的比较结果共有以下四种情况，分别需输出一些顶点。请问哪种情况下输出的顶点是正确的？

A：S在可见一侧，P在不可见一侧，则输出线段SP与裁剪线的交点Q

B：S和P均在可见的一侧，则输出0个顶点

C：S和P均在不可见的一侧，则输出S和P

D：S在不可见的一侧，P在可见的一侧，则输出S点和线段SP与裁剪线的交点


图中红点应编码为：

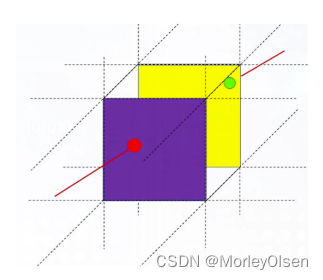
A：010001

B：100001

C：100000

D：110001


图中的裁剪类型为：

A：串精度裁剪

B：字符精度裁剪

C：笔划精度裁剪

D：像素精度裁剪

 

下述有关窗口和视区的描述哪个是错误的？

A：窗口是在世界坐标系中定义的，视区是在屏幕坐标系中定义的

B：窗口内一物体映射到视区时，假设窗口大小不变，当视区不断变大时，视区内显示的物体部分被缩小了

C：窗口区域总是大于视区的区域

D：窗口内一物体映射到视区时，假设视区大小不变，当窗口不断变小时，视区内显示的物体部分被放大了

三维空间点p(x,y,z)的规范化齐次坐标表示为哪一个？

A：(x,y,z)

B：(x,y,z,1)

C：(x,y,z,n)

D：(hx,hy,hz,hn)其中h不为1

有关矩阵运算说法正确的是？

A：任何两个矩阵都可以相乘

B：矩阵乘法满足交换律

C：矩阵乘法交换后结果一定不同

D：矩阵加法满足结合律

下列结论中，正确的答案是

A：零向量只有大小没有方向

B：对任一向量a，|a|>0总是成立的

C：向量AB和BA是相等的

D：两个相等的向量若起点相同，则终点必相同


一个三维物体使用下面的变换矩阵，将产生什么效果？

A：三维物体正投影到XOY面，即三视图中的俯视图

B：三维物体正投影到YOZ面，即三视图中的侧视图

C：三维物体斜投影到XOZ平面

D：三维物体正投影到XOZ面，即三视图中的主视图

 

在下列对投影的描述里，正确的论述为

A：太阳光线产生的投影为平行投影

B：三视图属于透视投影

C：物体经过透视投影后可产生缩放的效果

D：透视投影与平行投影相比，视觉效果更有真实感，而且能真是地反映物体的精确的尺寸和形状


使用下列二维图形变换矩阵，图形坐标[x,y,z]右乘该列变换矩阵，最终产生变换的结果为？

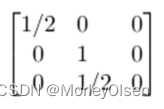
A：图形缩小1/2倍，沿X、Y坐标轴方向各移动1/2个绘图单位

B：沿Y坐标轴方向缩小1/2倍，沿X坐标轴方向移动1/2个绘图单位

C：图形放大2倍，沿X和Y坐标轴方向各移动1/2个绘图单位

D：沿X坐标轴方向缩小1/2倍，沿Y坐标轴方向移动1/2个绘图单位

 

下面关于深度缓存消隐算法（Z-Buffer）的论述，哪些是正确的

A：Z-Buffer算法需要开辟一个与图像大小相等的深度缓存数组

B：Z-Buffer算法没有利用图形的相关性与连续性

C：Z-Buffer算法是在像素级上的消隐算法，因此效率高

D：Z-Buffer算法占用空间小

下列有关曲线的论述哪些是正确的

A：在计算机图形学种，曲线的插值和拟合都可视为逼近

B：曲线的连续性分为参数和几何两种连续，其中参数连续性的条件高于几何连续性

C：参数方程的优势有更大的自由度来控制曲线、曲面的形状

D：给定N个控制点，可以有N+1条插值曲线

曲线参数化的本质是找到更多的插值多项式

A：正确

B：错误

下列有关曲线和曲面概念的叙述语句中，正确的论述为

A：实体模型和曲面造型是CAD系统中常用的主要造型方法

B：隐式表示和显式表示与坐标轴无关

C：参数曲线曲面有代数和几何两种表示形式

D：对切矢量求导可得曲率

双三次Bezier曲面的4条边界都是三次Bezier曲线，其特征网格的顶点个数是：

A：9

B：12

C：16

D：20

Bezier和B样条曲线的位置和形状只与特征多边形的顶点的位置有关，它不依赖坐标系的选择

A：对

B：错

相关文章：

【计算机图形学】课堂习题汇总

在直线的光栅化算法中&#xff0c;如果不考虑最大位移方向则可能得到怎样的直线&#xff1f; A&#xff1a;斜率为1的线 B&#xff1a;总是垂直的 C&#xff1a;离散的点&#xff0c;无法构成直线 D&#xff1a;总是水平的 在直线的改进的Bresenham算法中&#xff0c;每当误…...

编程日记 2023/4/30 6:47:43

国外导师对博士后申请简历的几点建议

正所谓“工欲善其事&#xff0c;必先利其器”&#xff0c;想要申请国外的博士后职位&#xff0c;就要准备好相应的申请文书材料。如果说Cover Letter是职位的窍门砖&#xff0c;那么申请者的简历就是争取职位的决定性筹码。 相信大家已经看过许多简历的模版了&#xff0c;但是…...

编程日记 2023/4/30 6:42:39

【五一创作】Scratch资料袋

Scratch软件是免费的、免费的、免费的。任何需要花钱才能下载Scratch软件的全是骗子。 1、什么是Scratch Scratch是麻省理工学院的“终身幼儿园团队”开发的一种图形化编程工具。是面向青少年的一款模块化&#xff0c;积木化、可视化的编程语言。 什么是模块化、积木化&…...

编程日记 2023/4/30 6:37:37

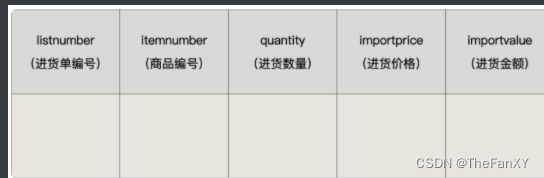
数据库基础篇 《17.触发器》

数据库基础篇 《17.触发器》 在实际开发中&#xff0c;我们经常会遇到这样的情况&#xff1a;有 2 个或者多个相互关联的表&#xff0c;如商品信息和库存信息分别存放在 2 个不同的数据表中&#xff0c;我们在添加一条新商品记录的时候&#xff0c;为了保证数据的完整性&#…...

编程日记 2023/4/30 6:32:36

03 - 大学生如何使用GPT

大学生如何使用GPT提高学习效率 一、引言 在当今的高速发展的信息时代&#xff0c;大学生面临着越来越多的学习挑战。作为一种先进的人工智能技术&#xff0c;GPT为大学生提供了一种强大的学习工具。本文将介绍大学生在不同场景中如何使用GPT来提高学习效率&#xff0c;并给出…...

编程日记 2023/4/30 6:27:35

【P1】Jmeter 准备工作

文章目录 一、Jmeter 介绍1.1、Jmeter 有什么样功能1.2、Jmeter 与 LoadRunner 比较1.3、常用性能测试工具1.4、性能测试工具如何选型1.5、学习 Jmeter 对 Java 编程的要求 二、Jmeter 软件安装2.1、官网介绍2.2、JDK 安装及环境配置2.3、Jmeter 三种模式2.4、主要配置介绍2.4.…...

编程日记 2023/4/30 6:22:34

字节的面试，你能扛住几道？

C &#xff0c; Python 哪一个更快&#xff1f; 读者答&#xff1a;这个我不知道从哪方面说&#xff0c;就是 C 的话&#xff0c;它其实能够提供开发者非常多的权限&#xff0c;就是说它能涉及到一些操作系统级别的一些操作&#xff0c;速度应该挺快。然后 Python 实现功能还…...

编程日记 2023/6/1 3:30:36

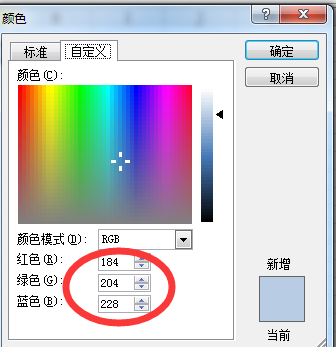
NOPI用法之自定义单元格背景色(3)

NPOI针对office2003使用HSSFWorkbook&#xff0c;对于offce2007及以上使用XSSFWorkbook&#xff1b;今天我以HSSFWorkbook自定义颜色为例说明&#xff0c;Office2007的未研究呢 在NPOI中默认的颜色类是HSSFColor&#xff0c;它内置的颜色有几十种供我们选择&#xff0c;如果不…...

编程日记 2023/5/30 4:54:59

数据分析中常见标准的参考文献

做数据分析过程中&#xff0c;有些分析法方法的标准随便一搜就能找到&#xff0c;不管是口口相传还是默认&#xff0c;大家都按那样的标准做了。日常分析不细究出处还可以&#xff0c;但是正式的学术论文你需要为你写下的每一句话负责&#xff0c;每一个判断标准都应该有参考文…...

编程日记 2023/4/30 6:07:31

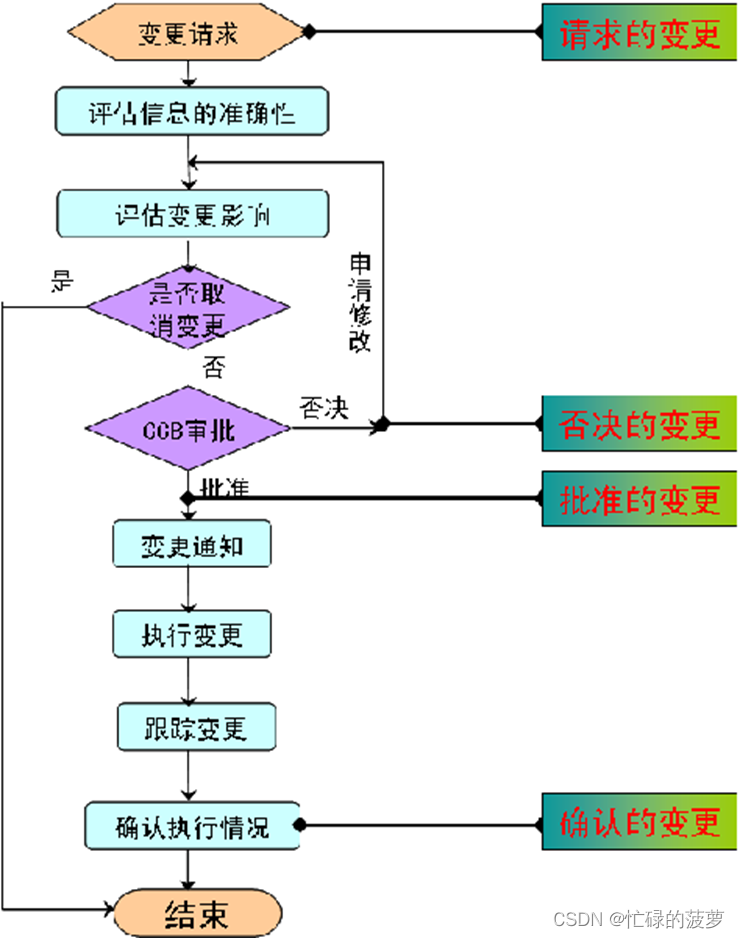
辨析 变更请求、批准的变更请求、实施批准的变更请求

变更请求、批准的变更请求、实施批准的变更请求辨析 辨析各种变更请求&#xff0c;不服来辨。 变更请求 定义&#xff1a;对正规受控的文件或计划(范围、进度、成本、政策、过程、计划或程序)等的变更&#xff0c;以反映修改或增加的意见或内容 根据变更请求的工作内容可将变…...

编程日记 2023/4/30 6:02:30

leetcode 561. 数组拆分

题目描述解题思路执行结果 leetcode 561. 数组拆分 题目描述 数组拆分 给定长度为 2n 的整数数组 nums &#xff0c;你的任务是将这些数分成 n 对, 例如 (a1, b1), (a2, b2), ..., (an, bn) &#xff0c;使得从 1 到 n 的 min(ai, bi) 总和最大。 返回该 最大总和 。 示例 1&am…...

编程日记 2023/6/1 3:31:41

AviatorScript

AviatorScript 是一门高性能、轻量级寄宿于 JVM &#xff08;包括 Android 平台&#xff09;之上的脚本语言 特性介绍 支持数字、字符串、正则表达式、布尔值、正则表达式等基本类型&#xff0c;完整支持所有 Java 运算符及优先级等。函数是一等公民&#xff0c;支持闭包和函…...

编程日记 2023/5/31 0:03:31

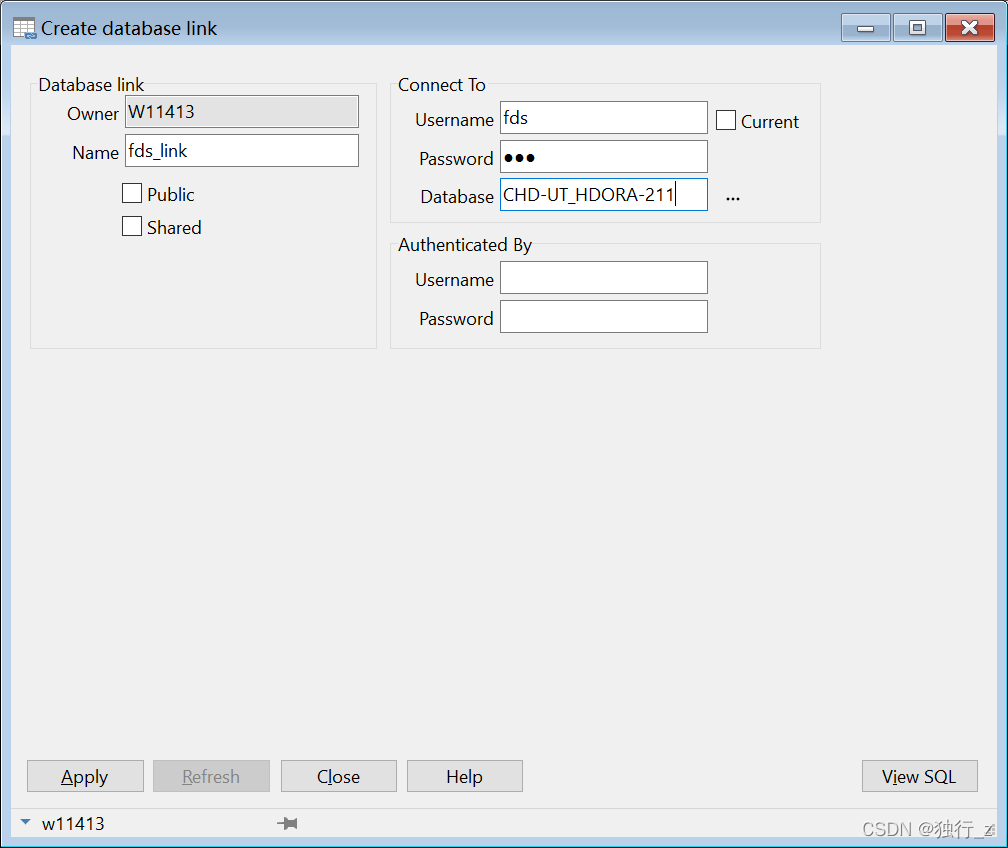
Oracle跨服务器取数——DBlink 初级使用

前言 一句话解释DBlink是干啥用的 实现跨库访问的可能性. 通过DBlink我们可以在A数据库访问到B数据库中的所有信息,例如我们在加工FDS层表时需要访问ODS层的表,这是就需要跨库访问 一、DBlink的分类 private&#xff1a;用户级别&#xff0c;只有创建该dblink的用户才可以使…...

编程日记 2023/5/31 9:19:29

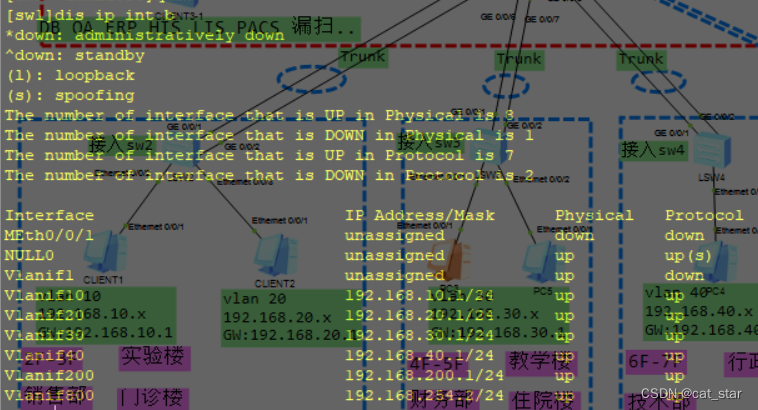
200人 500人 园区网设计

实验要求&#xff1a; ① 设置合理的STP优先级、边缘端口、Eth-trunk ② 企业内网划分多个vlan &#xff0c;减少广播域大小&#xff0c;提高网络稳定性 ③ 所有设备&#xff0c;在任何位置都可以telnet远程管理 ④ 出口配置NAT ⑤ 所有用户均为自动获取ip地址 ⑥ 在企业…...

编程日记 2023/4/30 5:42:26

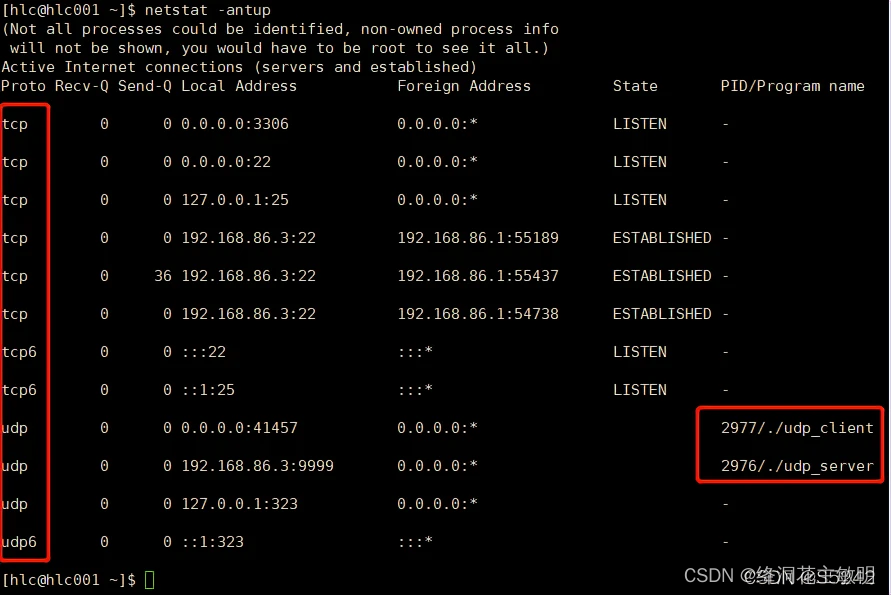
netstat命令解析

一、linux系统中netstat命令的帮助信息 └──╼ $netstat -h usage: netstat [-vWeenNcCF] [<Af>] -r netstat {-V|--version|-h|--help}netstat [-vWnNcaeol] [<Socket> ...]netstat { [-vWeenNac] -i | [-cnNe] -M | -s [-6tuw] }-r, --route …...

编程日记 2023/4/30 5:37:25

API接口的自我阐述

API&#xff08;Application Programming Interface&#xff09;&#xff0c;翻译为应用程序接口&#xff0c;是一套定义程序之间如何通讯的接口。API可以实现软件的可重用性、可维护性和互操作性&#xff0c;同时也可以提升软件的性能和安全性。API接口是一个软件系统中的重要…...

编程日记 2023/4/30 5:32:23

Day32内部类

内部类 内部类就是在一个类中定义一个类&#xff0c;&#xff08;在A类中定义一个B类&#xff0c;B类就被称为内部类&#xff09; 格式&#xff1a;public class 类名{ 修饰符 class 类名{} } 如&#xff1a;public class Outer{ public class Inner {} } //内部类可以访问外部…...

编程日记 2023/4/30 5:27:21

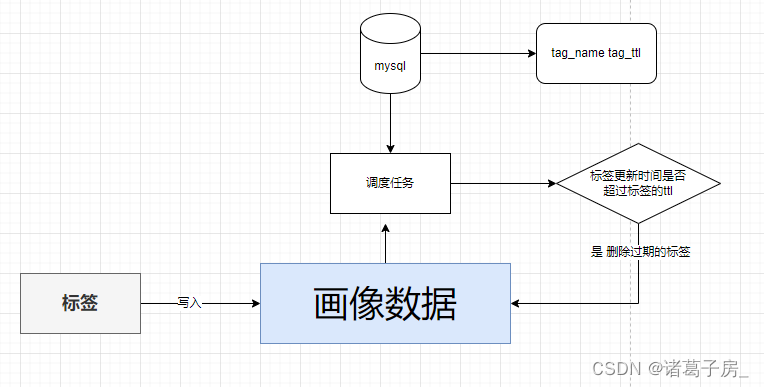
用户画像系列——HBase 在画像标签过期策略中的应用

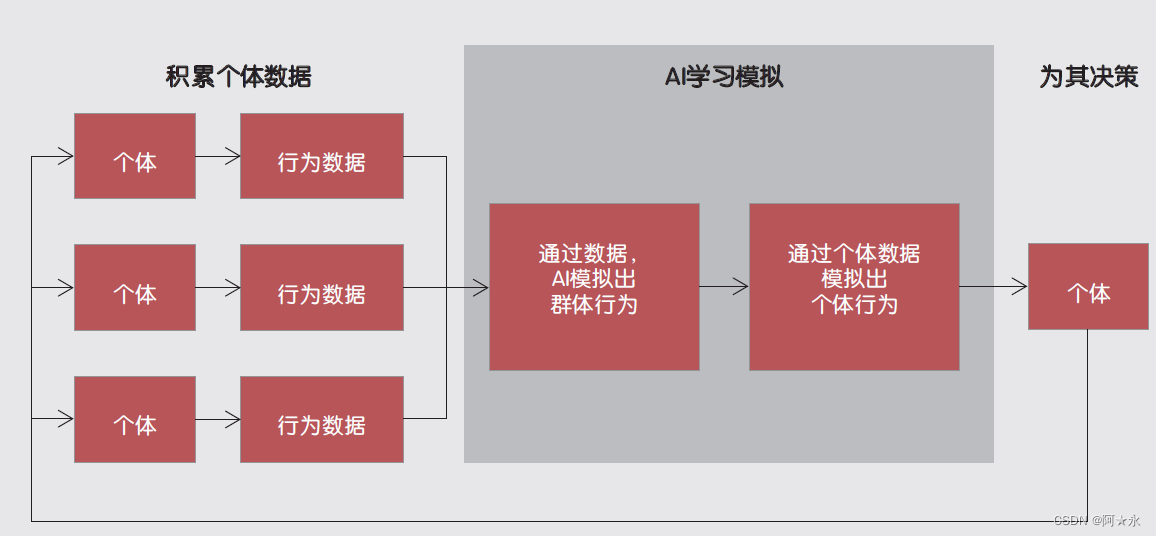
一、背景 前面系列文章介绍了用户画像的概念、用户画像的标签加工、用户画像的应用。本篇文章主要介绍一些画像的技术细节&#xff0c;让大家更加详细的了解画像数据存储和处理的逻辑 举个现实中的例子&#xff1a; 例子1&#xff1a;因为疫情原因&#xff0c;上线一个平台(…...

编程日记 2023/4/30 5:22:20

时下热门话题：ChatGPT能否取代人类？

时下热门话题&#xff1a;ChatGPT能否取代人类&#xff1f; 2022年11月底&#xff0c;人工智能对话聊天机器人ChatGPT推出&#xff0c;迅速在社交媒体上走红&#xff0c;短短5天&#xff0c;注册用户数就超过100万。2023年1月末&#xff0c;ChatGPT的月活用户已突破1亿&#x…...

编程日记 2023/4/30 5:17:19

每日刷题记录（十七）

目录 第一题&#xff1a;求12...n解题思路&#xff1a;代码实现&#xff1a; 第二题&#xff1a;两两交换链表中的节点解题思路&#xff1a;代码实现&#xff1a; 第三题&#xff1a;只出现一次的数字 II解题思路&#xff1a;代码实现&#xff1a; 第四题&#xff1a;根据字符串…...

编程日记 2023/4/30 5:12:18

开放原子训练营（第三季）RT-Thread Nano学习营一探究竟

前言 不知道从什么时候起&#xff0c;智能设备开始普及到了我们日常生活的方方面面。下班还未到家&#xff0c;热水器就可以调到合适的温度&#xff1b;上班刚进公司&#xff0c;忘关空调也不再是什么烦恼&#xff1b;诸如夜晚的灯光变换&#xff0c;白昼的窗帘适应等更给我们…...

编程日记 2023/6/1 11:13:21

数据库系统概论（二）关系数据库，SQL概述和数据库安全性

作者的话 前言&#xff1a;总结下知识点&#xff0c;自己偶尔看一看。 目录 一、关系模型概述 1.1关系数据结构及形式化定义 1.1.1域&#xff08;Domain&#xff09; 1.1.2笛卡尔积&#xff08;Cartesian Product&#xff09; 1.1.3关系&#xff08;Relation&#xff09; …...

编程日记 2023/4/30 5:02:16

【VM服务管家】VM4.x算子SDK开发_3.1 环境配置类

目录 3.1.1 环境配置&#xff1a;CSharp算子SDK开发环境配置方法3.1.2 算子封装&#xff1a;使用C封装算子SDK的方法3.1.3 异常中断&#xff1a;算子SDK软件运行报错“托管调试助手”中断的解决方法3.1.4 深度学习&#xff1a;GPU运行深度学习算子引发StackOverFlow异常的方法 …...

编程日记 2023/4/30 4:57:15

Java核心书籍1

1.《Java核心技术》是一本深入浅出的Java编程指南&#xff0c;适合初学者和有一定Java编程基础的读者。这本书的主要作者是Cay S. Horstmann和Gary Cornell&#xff0c;他们都是Java领域的知名专家。这本书的最新版本是第10版&#xff0c;其中涵盖了Java SE 9、10和11的新特性&…...

编程日记 2023/4/30 4:52:13

crontab详细用法 定时任务

使用crontab可以在指定时间执行一个shell脚本或者一系列Linux命令 crontab的使用方法 方法1.使用crontab命令 例如添加一个新的或者编辑已有的,使用: crontab -e就可以进入配置文件.此时配置crontab的执行者是当前登入用户,如果当前有用户是root,需要为其他用户配置,可以使用…...

编程日记 2023/4/30 4:47:12

基于ArcGIS Pro、Python、USLE、INVEST模型等多技术融合的生态系统服务构建生态安全格局

查看原文>>>基于ArcGIS Pro、Python、USLE、INVEST模型等多技术融合的生态系统服务构建生态安全格局 目录 第一章、生态安全评价理论及方法介绍 第二章、平台基础 第三章、数据获取与清洗 第四章、基于USLE模型的土壤侵蚀评价 第五章、基于风蚀修正模型的防风固…...

编程日记 2023/4/30 4:42:11

开心档之MySQL 创建数据类型

MySQL 数据类型 MySQL 中定义数据字段的类型对你数据库的优化是非常重要的。 MySQL 支持多种类型&#xff0c;大致可以分为三类&#xff1a;数值、日期/时间和字符串(字符)类型。 数值类型 MySQL 支持所有标准 SQL 数值数据类型。 这些类型包括严格数值数据类型(INTEGER、S…...

编程日记 2023/4/30 4:37:10

【C++ Primer(第5版) 课后习题题目及答案 第一章】

C Primer5th 课后习题答案 第一章 1.1&#xff1a;查阅你使用的编译器的文档&#xff0c;确定它所使用的文件命名约定。编译并运行main程序。1.2&#xff1a;改写程序&#xff0c;让它返回-1。返回值-1通常被当作程序错误的标识。重新编译并运行你的程序&#xff0c;观察你的系…...

编程日记 2023/4/30 4:32:08

【英语】100个句子记完7000个托福单词

其实主要的7000词其实是在主题归纳里面&#xff0c;不过过一遍100个句子也挺好的&#xff0c;反正也不多。 文章目录 Sentence 01Sentence 02Sentence 03Sentence 04Sentence 05Sentence 06Sentence 07Sentence 08Sentence 09Sentence 10Sentence 11Sentence 12Sentence 13Sent…...

编程日记 2023/4/30 4:27:06

六、CANdelaStudio入门-通信参数编辑

本专栏将由浅入深的展开诊断实际开发与测试的数据库编辑，包含大量实际开发过程中的步骤、使用技巧与少量对Autosar标准的解读。希望能对大家有所帮助，与大家共同成长，早日成为一名车载诊断、通信全栈工程师。 本文介绍CANdelaStudio的通信参数编辑，欢迎各位朋友订阅、评论，…...

编程日记 2023/6/1 3:33:37