带你搞懂人工智能、机器学习和深度学习!
不少高校的小伙伴找我聊入门人工智能该怎么起步,如何快速入门,多长时间能成长为中高级工程师(聊下来感觉大多数学生党就是焦虑,毕业即失业,尤其现在就业环境这么差),但聊到最后,很多小朋友连人工智能和机器学习、深度学习的关系都搞不清楚。
今天更文给大家科普一下这三者是什么及他们之间的关系,希望能帮到大家
人工智能
人工智能(Artificial Intelligence,简称 AI)这个词学术上是如何定义的呢?
美国麻省理工学院温斯顿教授认为:“人工智能就是研究如何使计算机去做过去只有人才能做的智能工作。另外有说“限制人工智能发展的是人的想象力”更使人工智能技术蒙上了一层浩瀚伟大的神秘外衣
人工智能的发展将会彻底改变人类的生产和生活方式,随之而来的是社会对人才需求的改变,即:就业趋势会逐渐偏向 AI 领域。
事实上,人工智能已经在各行各业的发展中扮演着重要的角色,并且它的地位还在不断地提升。
例如:人脸识别、自动驾驶、智能客服、短视频推荐、金融风控、智慧医疗、智慧农业、机器人技术等,这些都是人工智能在各个行业中的具体应用。
人工智能是一个不断发展和变化的领域,它是一个真正充满希望的行业。人工智能一方面使得其它职业容易被替代,另一方面也增加了 AI 技术人员的不可替代性。
接下来,聊一下机器学习与深度学习的概念以及它们和人工智能的关系,这是许多刚接触 AI 这个领域的人最容易混淆的几个概念。
机器学习
首先,什么是机器学习?它和人工智能有什么关系呢?
机器学习(Machine Learning,简称 ML)是从大量的经验数据中学习一种规律(或者称之为模型),从而实现人类所具备的一些能力。
举个栗子吧,比如我可以根据一个人的身高去预测他的体重,一定是因为我见过很多的人,并且了解了他们的身高和体重,才会有一个比较合理的判断。
那么我的这种判断能力可以让计算机学会吗?答案是肯定的。机器学习是人工智能的一种实现方式,也是最重要的实现方式。
首先,我们需要收集大量的身高和体重数据,然后根据这些数据画一个散点图:
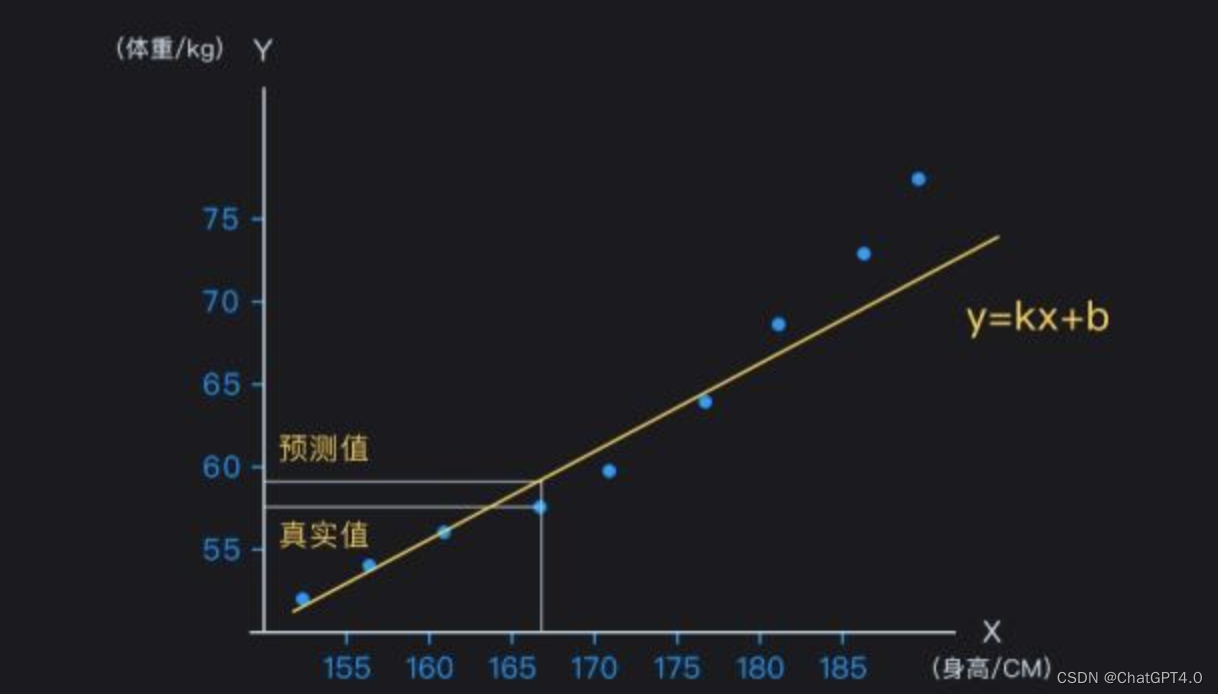
仔细观察,身高和体重的关系其实可以用高中所学的一次线性函数 f(x) = kx+b 来近似刻画,我们假设数据符合这样的规律,然后让计算机从数据中学习到函数的参数 k 和 b。
这里的 f(x) 可以理解为机器学习中的模型,换句话说,模型本质上是一个数学上的函数,也可以称之为从输入到输出的映射。
请你思考一个问题:计算机是如何从数据中学习到参数 k 和 b 的呢?
你可能会想到高中学过的一次线性函数的解法:先根据两点坐标确定斜率,然后得到点斜式直线方程。那么,计算机是这么做的吗?
计算机可不是这么解的。首先,选择哪两个点来确定斜率就是个问题。因为这些数据点并不是严格的一次线性关系,我们是用 f(x) = kx + b 来近似刻画数据的规律,所以计算机要做的是让这个近似的函数最大程度地拟合数据,进而使得误差最小化。
这其实也引出了机器学习的方法:最小化误差函数。这里的误差函数在机器学习中的术语叫做 经验风险或结构风险 。至于如何最小化,这又是一个知识点了,涉及到最优化算法。在后面的课程中,我会详细讲解经验风险、结构风险以及基本的最优化算法。
模型参数学习的思路是:先初始化参数 k 和 b,然后把数据点 (x,y) 的横坐标 x 代入一次线性函数得到预测值 f(x),根据预测值 f(x) 与真实值 y 的误差去调整参数,直到整体误差足够小时,停止学习。如图所示:

这幅图反映了模型 y=kx+b 对蓝色数据点的拟合情况,假如学习到的模型是 y = 0.34x+2,我们就可以根据 y = 0.34x + 2 来预测未知身高 x 对应的体重值 y了。
综上所述,机器学习本质上是数据驱动下的学习,而人类学习是靠过往的经验去学习。
AI、ML、DL的关系
我们经常听到的是深度学习(Deep Learning ,简称 DL)和人工智能这两个词。那么深度学习与人工智能有什么关系呢,机器学习和深度学习哪个概念的范畴更大一些呢?
答案是机器学习的范畴更大一些。具体来讲,深度学习是机器学习现在比较火的一个方向,其本身是神经网络算法的衍生,在图像、语音等富媒体的分类和识别上取得了非常好的效果。
所以,深度学习也是人工智能的一种重要的实现方式。下面这张图反映了AI、ML、DL 的从属关系和研究范畴大小:
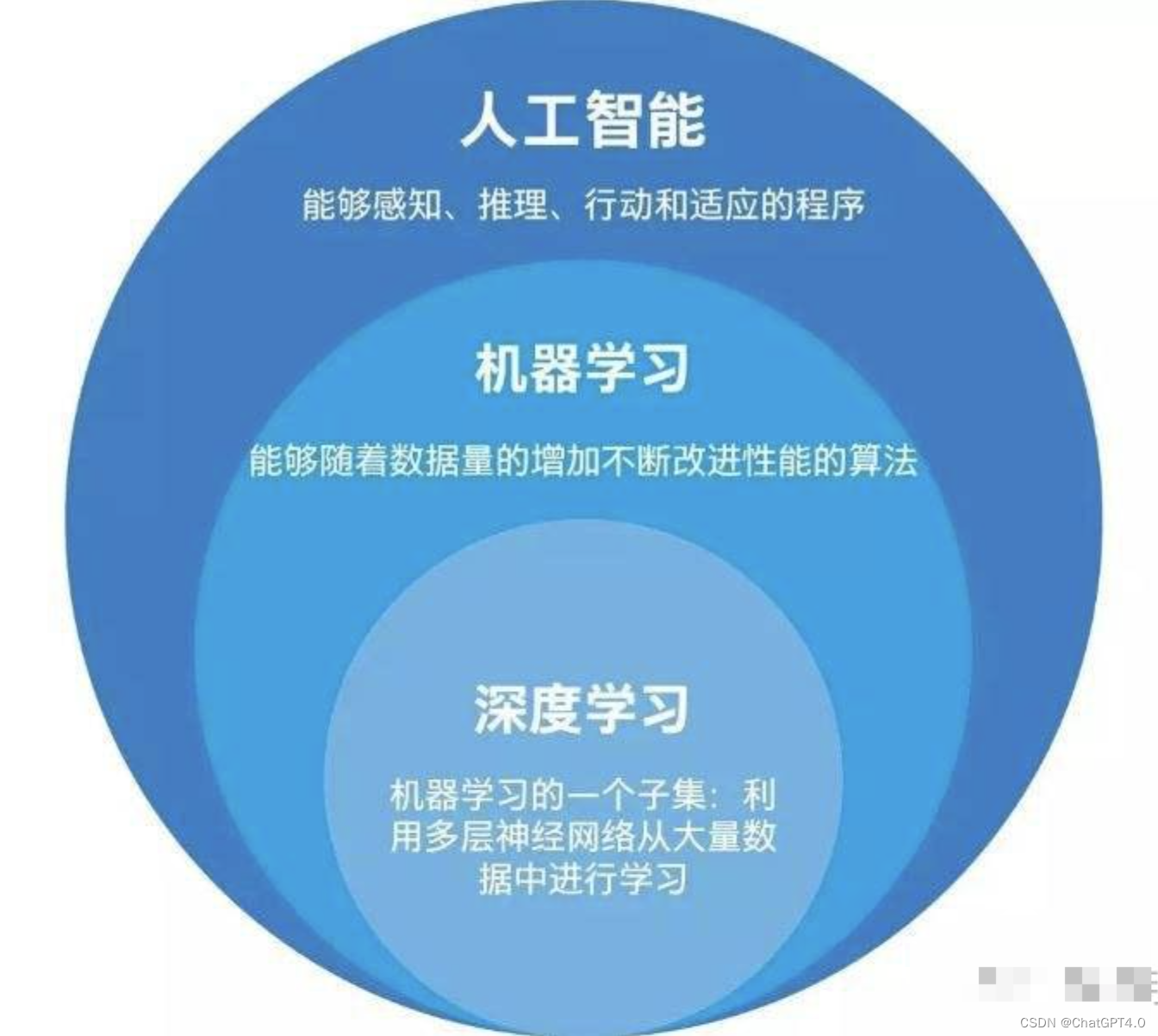
如果你有更简洁更合理的说法欢迎交流。
相关文章:

带你搞懂人工智能、机器学习和深度学习!
不少高校的小伙伴找我聊入门人工智能该怎么起步,如何快速入门,多长时间能成长为中高级工程师(聊下来感觉大多数学生党就是焦虑,毕业即失业,尤其现在就业环境这么差),但聊到最后,很多…...

Android 11.0 framework中Launcher的启动流程分析
1.前言 在11.0的系统rom定制化开发中,在rom定制过程中,在对于开发默认Launcher功能,解决开机动画后黑屏,了解fallbackhome机制等等 对于launcher的启动流程来说很重要,接下来就来分析下launcher的启动流程 2.framework中Launcher的启动流程分析的核心类 frameworks/ba…...

2023年第十五届华中杯赛题C 题 空气质量预测与预警
2023年五一假期期间,数学建模竞赛就有四场,各种比赛各种需求应接不暇。因此,对于本次浅析有不足的地方欢迎大家指出。为了更好的帮助大家华中杯参赛,下面带来,C题详细版思路。由于C题的难度,注定选题人数将…...
包、变量、函数)
Go官方指南(一)包、变量、函数
import "time" 获取当前系统时间:time.Now() 每个 Go 程序都是由包构成的 按照约定 ,包名与导入路径的最后一个元素一致。例如,"math/rand"包中的源码均以 package rand 语句开始 在 Go 中,如果一个名字以…...
liunx笔记
快捷键 #移动到行首 ctrla #移动到行尾 ctrle #删除光标之前的字符 ctrlu #删除光标之后的字符 ctrlk #清屏 ctrll正则表达式 正则中普通常用的元字符 元字符功能.匹配除了换行符以外的任意单个字符*前导字符出现0次或连续多次.*任意长度字符^行首(以…开头),如…...
vue3 封装ECharts组件
一、前言 前端开发需要经常使用ECharts图表渲染数据信息,在一个项目中我们经常需要使用多个图表,选择封装ECharts组件复用的方式可以减少代码量,增加开发效率。 ECharts图表大家应该用的都比较多,基础的用法就不细说了ÿ…...

Spring Security 6.0系列【30】授权服务器篇之JOSE规范
有道无术,术尚可求,有术无道,止于术。 本系列Spring Boot 版本 3.0.4 本系列Spring Security 版本 6.0.2 本系列Spring Authorization Server 版本 1.0.2 源码地址:https://gitee.com/pearl-organization/study-spring-security-demo 文章目录 1. 前言2. JOSE 规范3. JW…...

维度表设计原则
维度的作用一般是查询约束、分类汇总以及排序等,我们在进行维度表设计时,应当提前考虑: (1)维度属性尽量丰富,为数据使用打下基础 比如淘宝商品维度有近百个维度属性,为下游的数据统计、分析、…...

【requests模块上】——02爬虫基础——如桃花来
目录索引 requests请求:1. 基于get请求:*基础写法:**带参数的get请求:* 2. 基于post请求: 获取数据:1. 获取json数据:2. 获取二进制数据: 初步伪装小爬虫——添加headers: 引入&…...
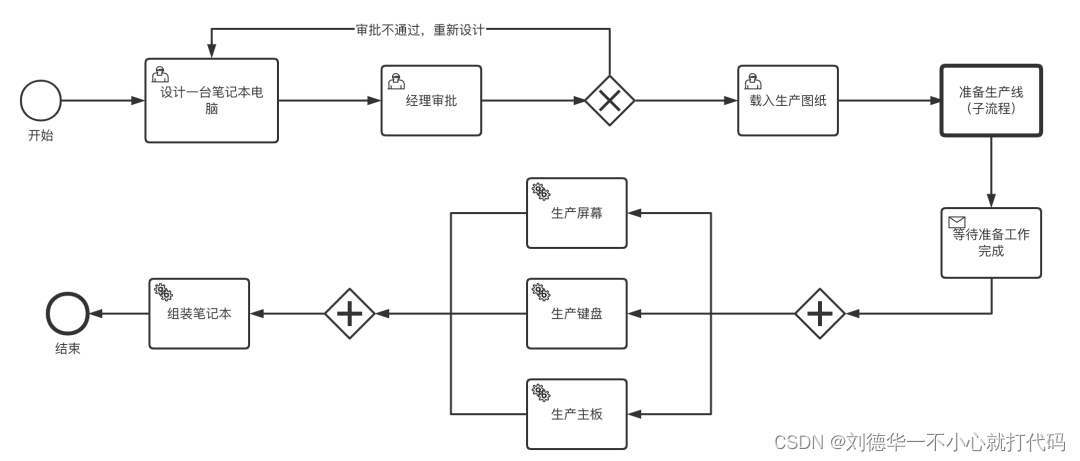
Springboot +Flowable,详细解释啥叫流程实例(一)
一.简介 上一篇中学习了Flowable 中的流程模板(流程定义)的部署问题,这一篇来学习什么叫流程实例。 部署之后的流程模板,还不能直接运行,例如我们部署了一个请假流程,现在 张三想要请假,他就需…...
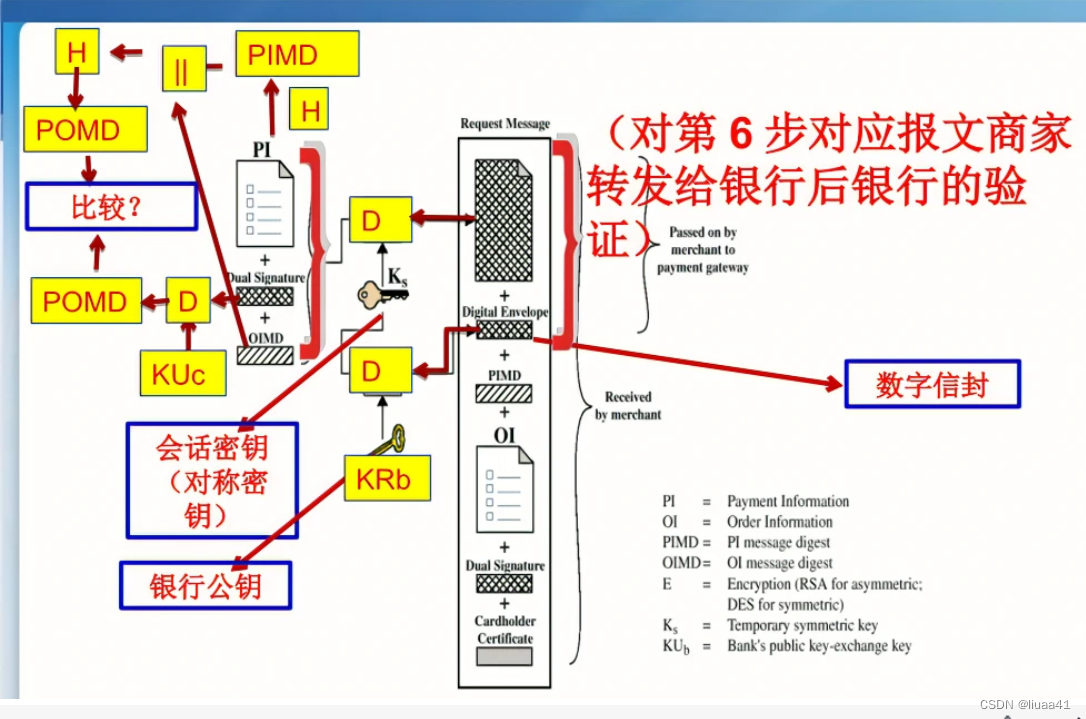
信息安全复习十:Web与电子商务安全
一、章节梗概 1.信息安全的学科内容 2.Web和电子商务安全问题提出 3.安全套接字协议SSL与传输层安全协议TLS 4.安全电子交易(SET)简要介绍 复习: 密码学内容:对称密钥密码、公开密钥密码、报文鉴别 PKI:数字签名、数字证书、信任关系 身份认…...

flutter 启动其他app server或者页面失败
1.目标Service 设置 android:exported"true" 2.目标Service需要声明自定义权限。客户端需要声明权限。 3.目标Service需要添加<intent-filter></intent-filter> 检查以上的声明和权限, 如果还是不行 说明是 Android 11引入了*包可见性*’ …...

【linux-进程2】进程控制
🌈环境变量 🍄初识 系统带的命令可以直接运行(ls ll命令等),但是我们自己写的命令必须要带上路径才能运行(./myproc),这是什么原因导致的?如果我们也想自己写的命令直接…...

【五一创作】多域名环境和Office 365混合部署方案
目录 一、多域名环境是什么? 二、Office 365是什么? 三、多域名环境与Office 365的结合 总结 一、多域名环境是什么? 多域名环境指的是一个企业拥有多个域名,这些域名可能隶属于不同的子公司、部门或者品牌,但是都归属于同一个母公司。例如,一个中国电信集团旗下有…...

Vue:路由route
一、概念 1、组成 每一个路由都由 key 和 value 组成。 keyvalue路由 route。 2、本质 路由的本质:一个路由表达了一组对应关系。路由器的本质:管理多组对应关系。 3、路由的工作原理 点击之后路径变化——>路由器监视到变化——>根据路径…...

Windows系统被faust勒索病毒攻击勒索病毒解密服务器与数据库解密恢复
在近期,一种名为faust后缀的勒索病毒威胁已经引起了全球计算机系统安全领域的关注。faust勒索病毒是一种基于RSA加密算法的恶意软件,能够加密目标计算机系统上的所有文件,并向用户勒索赎金来承诺解密恢复操作。下面为大家介绍一下Windows系统…...
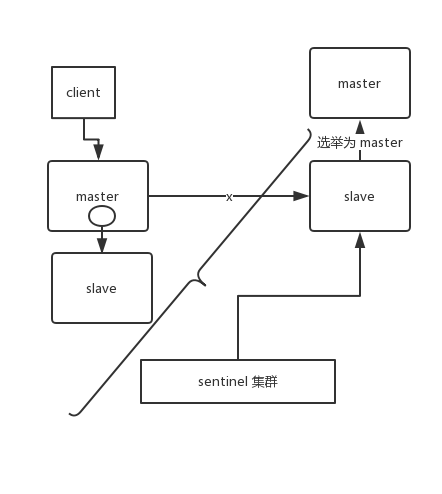
Java面试题总结 | Java面试题总结7- Redis模块(持续更新)
Redis 文章目录 Redisredis的线程模型Redis的Mysql的区别Redis和传统的关系型数据库有什么不同?Redis常见的数据结构zset数据结构Redis中rehash过程redis为什么不考虑线程安全的问题呢Redis单线程为什么还能这么快?为什么Redis是单线程的?red…...

虹科案例 | 如何通过智能、非接触式测量解决方案,提高起重机的安全和效率?
PART 1 案例详情 自建造初期以来,起重机行业已经走了很长一段路。技术的使用在行业进步中发挥了重要作用,降低了使用桥式起重机的危险性。特别是,智能、非接触式测量解决方案通过使用高架升降机更安全、更高效、更高效,为行业的进…...
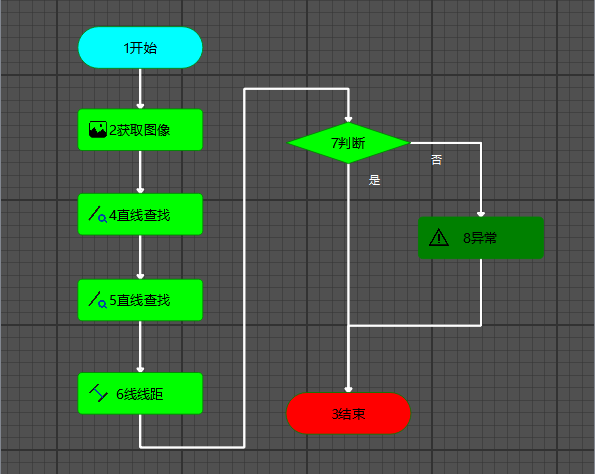
流程图拖拽视觉编程-流程编辑器
目录 一、简介 二、流程编辑器-视图实现 三、参考资料 一、简介 前期文章: 流程图拖拽视觉编程--概述_Jason~shen的博客-CSDN博客 本期内容: 本期将介绍流程编辑器模块的实现方法,效果图如下所示。该模块基于QT Graphics/View实现&…...

6.hashcode与equals区别与联系
1.hashCode介绍 hashCode() 的作用是获取哈希码,也称为散列码;它实际上是返回一个int整数。 这个哈希码的作用是确定该对象在哈希表中的索引位置。hashCode() 定义在JDK的Object.java中,这就意味着Java中的任何类都包含有hashCode() 函数。 2.equals介…...
)
Java 语言特性(面试系列2)
一、SQL 基础 1. 复杂查询 (1)连接查询(JOIN) 内连接(INNER JOIN):返回两表匹配的记录。 SELECT e.name, d.dept_name FROM employees e INNER JOIN departments d ON e.dept_id d.dept_id; 左…...

K8S认证|CKS题库+答案| 11. AppArmor
目录 11. AppArmor 免费获取并激活 CKA_v1.31_模拟系统 题目 开始操作: 1)、切换集群 2)、切换节点 3)、切换到 apparmor 的目录 4)、执行 apparmor 策略模块 5)、修改 pod 文件 6)、…...

React hook之useRef
React useRef 详解 useRef 是 React 提供的一个 Hook,用于在函数组件中创建可变的引用对象。它在 React 开发中有多种重要用途,下面我将全面详细地介绍它的特性和用法。 基本概念 1. 创建 ref const refContainer useRef(initialValue);initialValu…...

工业安全零事故的智能守护者:一体化AI智能安防平台
前言: 通过AI视觉技术,为船厂提供全面的安全监控解决方案,涵盖交通违规检测、起重机轨道安全、非法入侵检测、盗窃防范、安全规范执行监控等多个方面,能够实现对应负责人反馈机制,并最终实现数据的统计报表。提升船厂…...

质量体系的重要
质量体系是为确保产品、服务或过程质量满足规定要求,由相互关联的要素构成的有机整体。其核心内容可归纳为以下五个方面: 🏛️ 一、组织架构与职责 质量体系明确组织内各部门、岗位的职责与权限,形成层级清晰的管理网络…...

Axios请求超时重发机制
Axios 超时重新请求实现方案 在 Axios 中实现超时重新请求可以通过以下几种方式: 1. 使用拦截器实现自动重试 import axios from axios;// 创建axios实例 const instance axios.create();// 设置超时时间 instance.defaults.timeout 5000;// 最大重试次数 cons…...

【碎碎念】宝可梦 Mesh GO : 基于MESH网络的口袋妖怪 宝可梦GO游戏自组网系统
目录 游戏说明《宝可梦 Mesh GO》 —— 局域宝可梦探索Pokmon GO 类游戏核心理念应用场景Mesh 特性 宝可梦玩法融合设计游戏构想要素1. 地图探索(基于物理空间 广播范围)2. 野生宝可梦生成与广播3. 对战系统4. 道具与通信5. 延伸玩法 安全性设计 技术选…...

OPenCV CUDA模块图像处理-----对图像执行 均值漂移滤波(Mean Shift Filtering)函数meanShiftFiltering()
操作系统:ubuntu22.04 OpenCV版本:OpenCV4.9 IDE:Visual Studio Code 编程语言:C11 算法描述 在 GPU 上对图像执行 均值漂移滤波(Mean Shift Filtering),用于图像分割或平滑处理。 该函数将输入图像中的…...

Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信
文章目录 Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信前言一、网络通信基础概念二、服务端与客户端的完整流程图解三、每一步的详细讲解和代码示例1. 创建Socket(服务端和客户端都要)2. 绑定本地地址和端口&#x…...

Java毕业设计:WML信息查询与后端信息发布系统开发
JAVAWML信息查询与后端信息发布系统实现 一、系统概述 本系统基于Java和WML(无线标记语言)技术开发,实现了移动设备上的信息查询与后端信息发布功能。系统采用B/S架构,服务器端使用Java Servlet处理请求,数据库采用MySQL存储信息࿰…...
