霍兰德人格分析雷达图
雷达图 Radar Chart
雷达图是多特性直观展示的重要方式
问题分析
霍兰德认为:人格兴趣与职业之间应有一种内在的对应关系
人格分类:研究型、艺术型、社会型、企业型、传统型、现实性
职业:工程师、实验员、艺术家、推销员、记事员、社会工作者
需求:雷达图方式验证霍兰德人格分析 - 输入:各职业人群结合兴趣的调研数据 - 输出:雷达图
分析:
这段代码的作用是绘制一个极坐标系下的雷达图,其中包含了职业类型和对应的6个特质分数的数据。具体步骤如下:
-
导入所需的库:numpy和matplotlib.pyplot。
-
设置中文标签显示:将默认字体设置为中文黑体。
-
定义数据:一个6行6列的矩阵,表示6个职业的6个特质分数。
-
定义角度:使用numpy的linspace函数生成6个角度,作为雷达图的x轴坐标。
-
重复第一个角度:为了让图像闭合,将第一个角度再添加到数组的最后。
-
定义职业标签:一个包含7个字符串元素的列表。
-
绘制雷达图:通过循环绘制每个职业的特质分数图形。在循环中,使用ax.plot函数绘制特质分数的折线图,并使用ax.fill函数填充颜色。
-
添加坐标轴标签:使用ax.set_thetagrids函数添加角度轴的标签。
-
添加标题:使用plt.title函数添加图表标题。
-
添加图例:使用plt.legend函数添加图例。
-
显示图形:使用plt.show函数显示图形。
代码:
# -- coding: utf-8 --
import numpy as np
import matplotlib.pyplot as plt
# 如果需要使用中文标签,还需添加以下代码
plt.rcParams['font.sans-serif'] = ['SimHei'] # 指定默认字体为中文黑体
# 数据
data = [[0.40, 0.32, 0.35, 0.30, 0.30, 0.88],[0.85, 0.75, 0.30, 0.25, 0.20, 0.40],[0.43, 0.89, 0.30, 0.28, 0.22, 0.30],[0.20, 0.30, 0.85, 0.45, 0.32, 0.25],[0.19, 0.22, 0.40, 0.90, 0.92, 0.28],[0.62, 0.55, 0.27, 0.25, 0.35, 0.30]]# 角度(弧度)
angles = np.linspace(0, 2*np.pi, 6, endpoint=False)# 重复第一个角度以使图像闭合
angles = np.concatenate((angles, [angles[0]]))# 职业
occupations = ['工程师', '实验员', '艺术家', '推销员', '记事员', '社会工作者', '技术员']# 绘图
fig = plt.figure()
ax = fig.add_subplot(111, polar=True)
for i in range(len(data)):# 绘制折线图ax.plot(angles, data[i]+data[i][:1], 'o-', linewidth=2, label=occupations[i])# 填充颜色ax.fill(angles, data[i]+data[i][:1], alpha=0.25)
# 添加坐标轴标签
ax.set_thetagrids(angles*180/np.pi, occupations)
# 添加标题
plt.title('Holland Personality Analysis', fontsize=20)
# 添加图例
plt.legend(loc='best')
# 显示图形
plt.show()
效果:

相关文章:

霍兰德人格分析雷达图
雷达图 Radar Chart 雷达图是多特性直观展示的重要方式 问题分析 霍兰德认为:人格兴趣与职业之间应有一种内在的对应关系 人格分类:研究型、艺术型、社会型、企业型、传统型、现实性 职业:工程师、实验员、艺术家、推销员、记事员、社会工…...

《Odoo开发者模式必知必会》—— 缘起
Odoo作为业界优秀的开源商务软件,在全球范围内拥有广泛的使用者。在领英国际,可以搜索到全球很多国家都有大量odoo人才需求的招聘信息。在国内,虽然已经有为数不少的企业,他们或者已经使用odoo,或者正在了解odoo&#…...

Java8的Options介绍
Java8引入了一个名为 Options 的新类,它是一个容器,可以保存单个值或根本不保存任何值。Optional目的是提供一种更优雅的方式来处理 null 值,这通常会导致NullPointerException。在这篇博客文章中,我们将探索如何在 Java8中使用 O…...
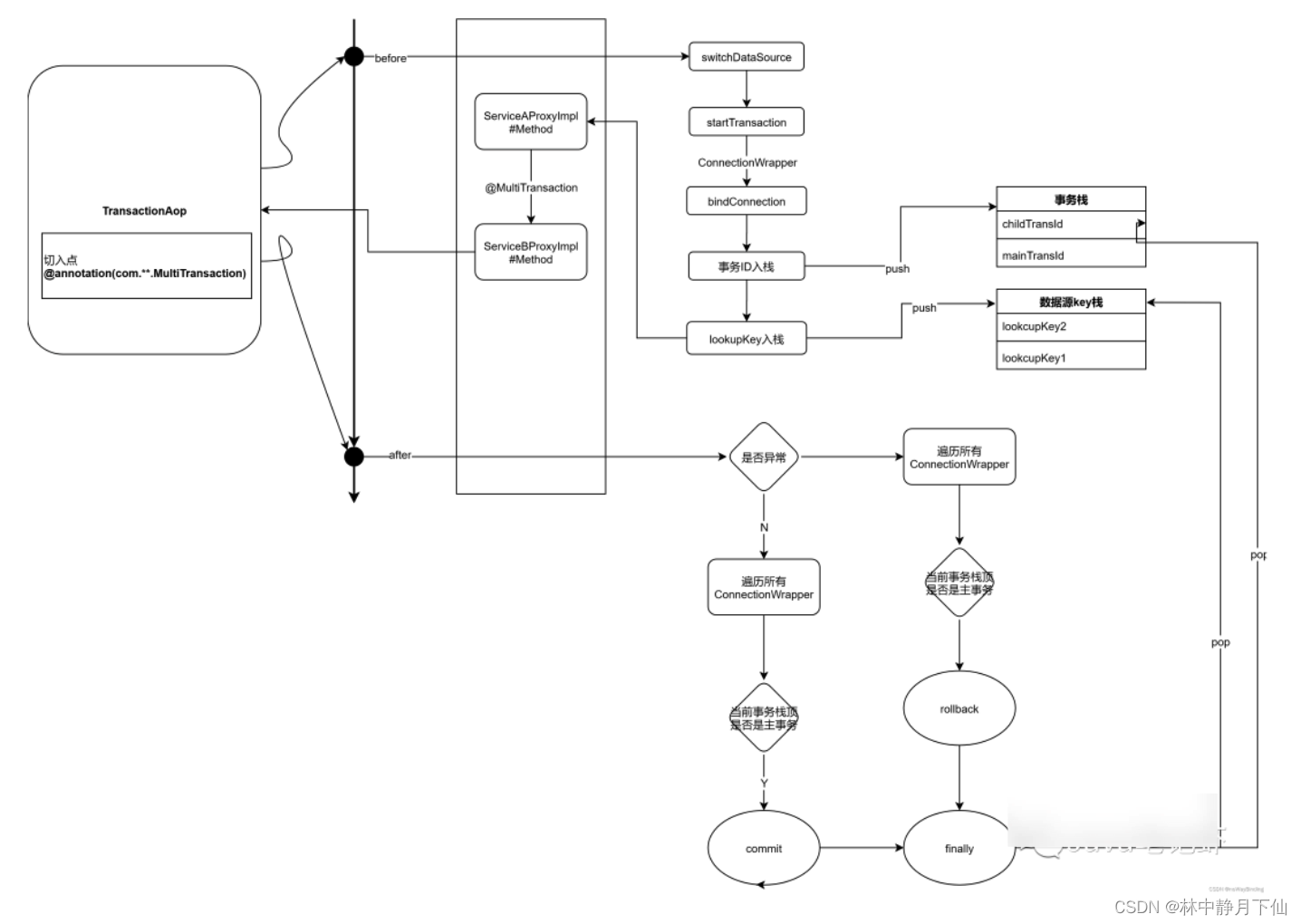
SpringBoot 多数据源及事务解决方案
1. 背景 一个主库和N个应用库的数据源,并且会同时操作主库和应用库的数据,需要解决以下两个问题: 如何动态管理多个数据源以及切换? 如何保证多数据源场景下的数据一致性(事务)? 本文主要探讨这两个问题的解决方案…...

tcpdump使用教程
一、概述 tcpdump是一个功能强大的,用于抓取网络数据包的命令行工具,与带界面的Wireshark一样,基于libpcap库构建。这篇文章主要介绍tcpdump的使用。关于如何使用tcpdump的资料中,最有用的就是tcpdump的两个手册。 tcpdump使用手…...
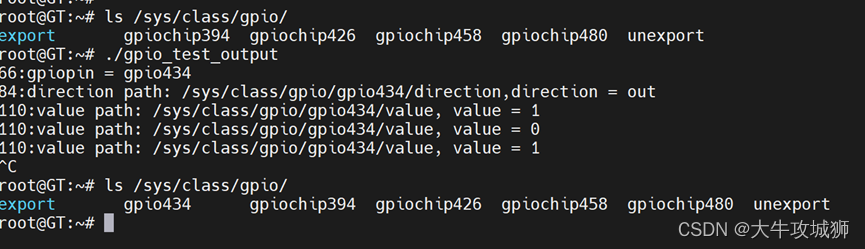
Zynq-7000、FMQL45T900的GPIO控制(五)---linux应用层配置GPIO输出控制
上文中详细阐述了对应原理图MIO/EMIO的编号,怎么计算获取linux下gpio的编号 本文涉及C代码上传,下载地址 Zynq-7000、FMQL45T900的GPIO控制c语言代码资源-CSDN文库 本文详细记录一下针对获取到gpio的编号,进行配置输出模式,并进…...
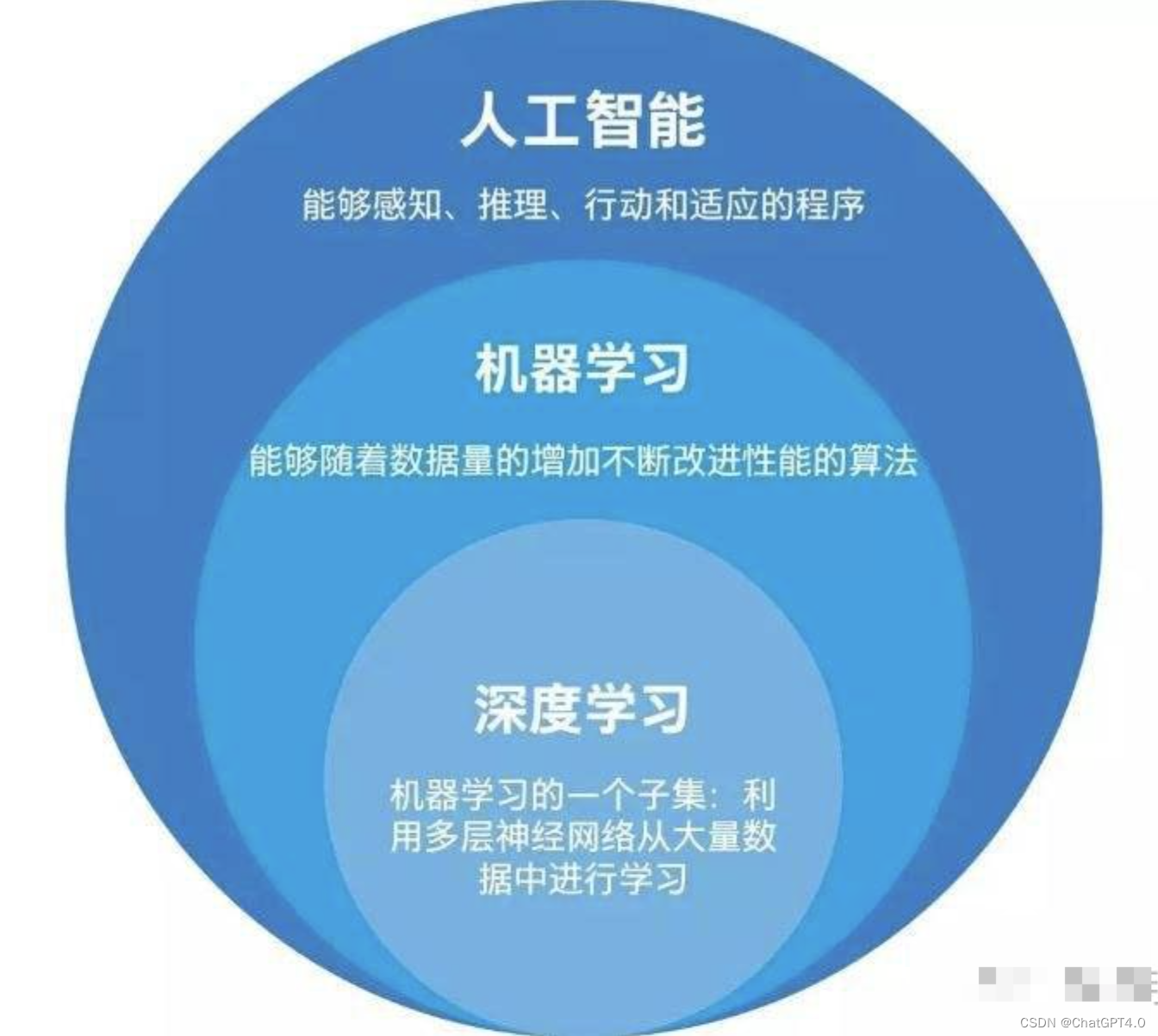
带你搞懂人工智能、机器学习和深度学习!
不少高校的小伙伴找我聊入门人工智能该怎么起步,如何快速入门,多长时间能成长为中高级工程师(聊下来感觉大多数学生党就是焦虑,毕业即失业,尤其现在就业环境这么差),但聊到最后,很多…...

Android 11.0 framework中Launcher的启动流程分析
1.前言 在11.0的系统rom定制化开发中,在rom定制过程中,在对于开发默认Launcher功能,解决开机动画后黑屏,了解fallbackhome机制等等 对于launcher的启动流程来说很重要,接下来就来分析下launcher的启动流程 2.framework中Launcher的启动流程分析的核心类 frameworks/ba…...

2023年第十五届华中杯赛题C 题 空气质量预测与预警
2023年五一假期期间,数学建模竞赛就有四场,各种比赛各种需求应接不暇。因此,对于本次浅析有不足的地方欢迎大家指出。为了更好的帮助大家华中杯参赛,下面带来,C题详细版思路。由于C题的难度,注定选题人数将…...
包、变量、函数)
Go官方指南(一)包、变量、函数
import "time" 获取当前系统时间:time.Now() 每个 Go 程序都是由包构成的 按照约定 ,包名与导入路径的最后一个元素一致。例如,"math/rand"包中的源码均以 package rand 语句开始 在 Go 中,如果一个名字以…...
liunx笔记
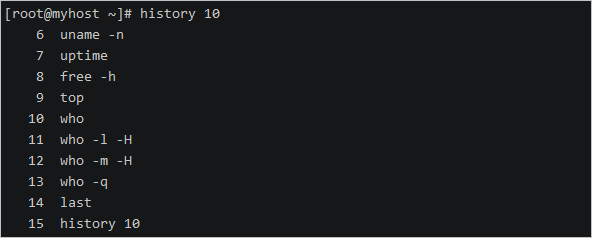
快捷键 #移动到行首 ctrla #移动到行尾 ctrle #删除光标之前的字符 ctrlu #删除光标之后的字符 ctrlk #清屏 ctrll正则表达式 正则中普通常用的元字符 元字符功能.匹配除了换行符以外的任意单个字符*前导字符出现0次或连续多次.*任意长度字符^行首(以…开头),如…...
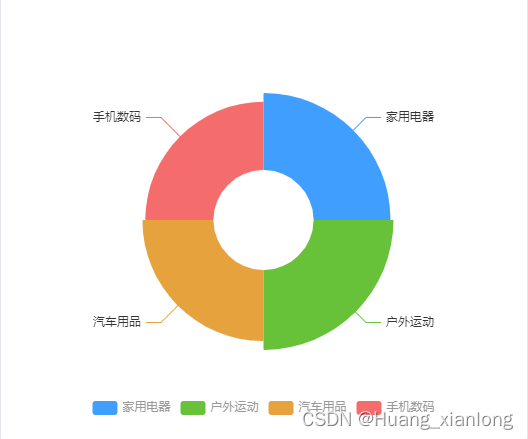
vue3 封装ECharts组件
一、前言 前端开发需要经常使用ECharts图表渲染数据信息,在一个项目中我们经常需要使用多个图表,选择封装ECharts组件复用的方式可以减少代码量,增加开发效率。 ECharts图表大家应该用的都比较多,基础的用法就不细说了ÿ…...

Spring Security 6.0系列【30】授权服务器篇之JOSE规范
有道无术,术尚可求,有术无道,止于术。 本系列Spring Boot 版本 3.0.4 本系列Spring Security 版本 6.0.2 本系列Spring Authorization Server 版本 1.0.2 源码地址:https://gitee.com/pearl-organization/study-spring-security-demo 文章目录 1. 前言2. JOSE 规范3. JW…...

维度表设计原则
维度的作用一般是查询约束、分类汇总以及排序等,我们在进行维度表设计时,应当提前考虑: (1)维度属性尽量丰富,为数据使用打下基础 比如淘宝商品维度有近百个维度属性,为下游的数据统计、分析、…...

【requests模块上】——02爬虫基础——如桃花来
目录索引 requests请求:1. 基于get请求:*基础写法:**带参数的get请求:* 2. 基于post请求: 获取数据:1. 获取json数据:2. 获取二进制数据: 初步伪装小爬虫——添加headers: 引入&…...
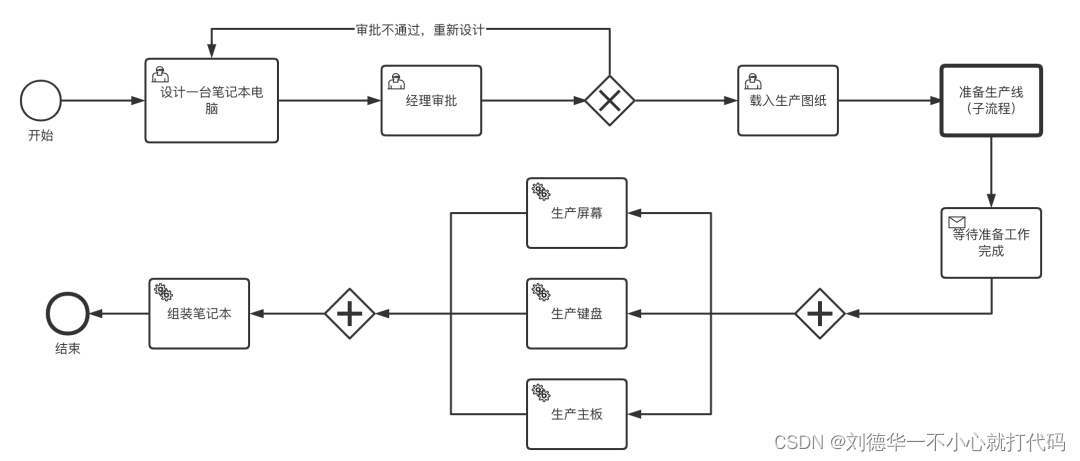
Springboot +Flowable,详细解释啥叫流程实例(一)
一.简介 上一篇中学习了Flowable 中的流程模板(流程定义)的部署问题,这一篇来学习什么叫流程实例。 部署之后的流程模板,还不能直接运行,例如我们部署了一个请假流程,现在 张三想要请假,他就需…...
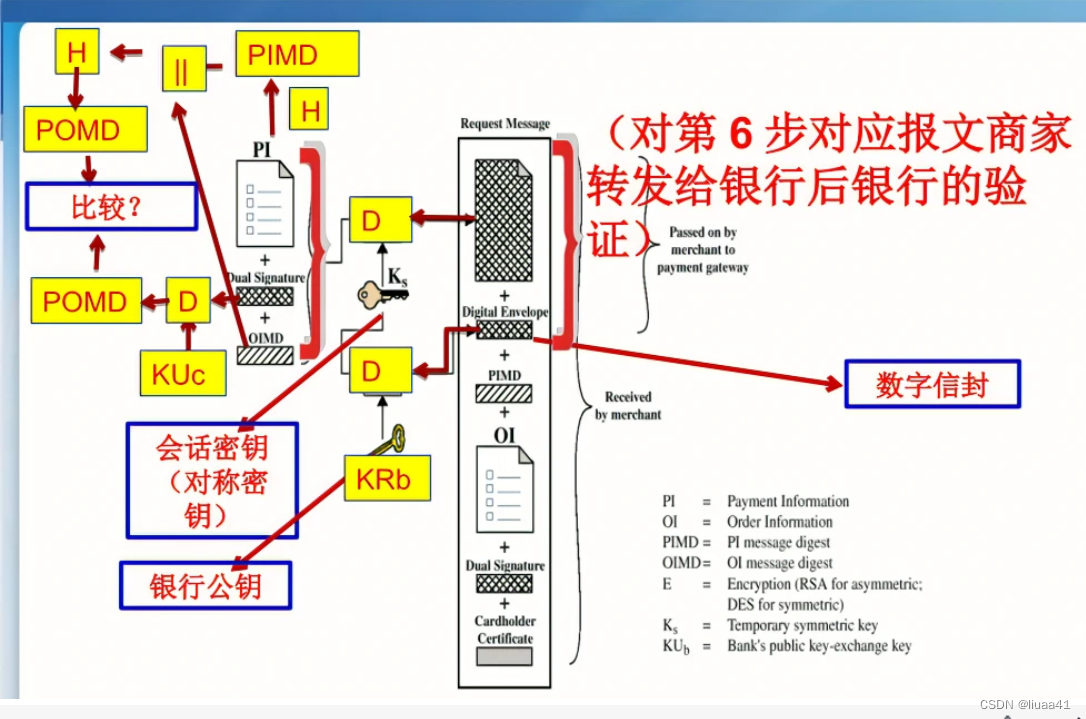
信息安全复习十:Web与电子商务安全
一、章节梗概 1.信息安全的学科内容 2.Web和电子商务安全问题提出 3.安全套接字协议SSL与传输层安全协议TLS 4.安全电子交易(SET)简要介绍 复习: 密码学内容:对称密钥密码、公开密钥密码、报文鉴别 PKI:数字签名、数字证书、信任关系 身份认…...

flutter 启动其他app server或者页面失败
1.目标Service 设置 android:exported"true" 2.目标Service需要声明自定义权限。客户端需要声明权限。 3.目标Service需要添加<intent-filter></intent-filter> 检查以上的声明和权限, 如果还是不行 说明是 Android 11引入了*包可见性*’ …...

【linux-进程2】进程控制
🌈环境变量 🍄初识 系统带的命令可以直接运行(ls ll命令等),但是我们自己写的命令必须要带上路径才能运行(./myproc),这是什么原因导致的?如果我们也想自己写的命令直接…...

【五一创作】多域名环境和Office 365混合部署方案
目录 一、多域名环境是什么? 二、Office 365是什么? 三、多域名环境与Office 365的结合 总结 一、多域名环境是什么? 多域名环境指的是一个企业拥有多个域名,这些域名可能隶属于不同的子公司、部门或者品牌,但是都归属于同一个母公司。例如,一个中国电信集团旗下有…...

家政维修平台实战20:权限设计
目录 1 获取工人信息2 搭建工人入口3 权限判断总结 目前我们已经搭建好了基础的用户体系,主要是分成几个表,用户表我们是记录用户的基础信息,包括手机、昵称、头像。而工人和员工各有各的表。那么就有一个问题,不同的角色…...

linux 错误码总结
1,错误码的概念与作用 在Linux系统中,错误码是系统调用或库函数在执行失败时返回的特定数值,用于指示具体的错误类型。这些错误码通过全局变量errno来存储和传递,errno由操作系统维护,保存最近一次发生的错误信息。值得注意的是,errno的值在每次系统调用或函数调用失败时…...

[10-3]软件I2C读写MPU6050 江协科技学习笔记(16个知识点)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16...

【git】把本地更改提交远程新分支feature_g
创建并切换新分支 git checkout -b feature_g 添加并提交更改 git add . git commit -m “实现图片上传功能” 推送到远程 git push -u origin feature_g...

在web-view 加载的本地及远程HTML中调用uniapp的API及网页和vue页面是如何通讯的?
uni-app 中 Web-view 与 Vue 页面的通讯机制详解 一、Web-view 简介 Web-view 是 uni-app 提供的一个重要组件,用于在原生应用中加载 HTML 页面: 支持加载本地 HTML 文件支持加载远程 HTML 页面实现 Web 与原生的双向通讯可用于嵌入第三方网页或 H5 应…...

4. TypeScript 类型推断与类型组合
一、类型推断 (一) 什么是类型推断 TypeScript 的类型推断会根据变量、函数返回值、对象和数组的赋值和使用方式,自动确定它们的类型。 这一特性减少了显式类型注解的需要,在保持类型安全的同时简化了代码。通过分析上下文和初始值,TypeSc…...

Linux中《基础IO》详细介绍
目录 理解"文件"狭义理解广义理解文件操作的归类认知系统角度文件类别 回顾C文件接口打开文件写文件读文件稍作修改,实现简单cat命令 输出信息到显示器,你有哪些方法stdin & stdout & stderr打开文件的方式 系统⽂件I/O⼀种传递标志位…...

麒麟系统使用-进行.NET开发
文章目录 前言一、搭建dotnet环境1.获取相关资源2.配置dotnet 二、使用dotnet三、其他说明总结 前言 麒麟系统的内核是基于linux的,如果需要进行.NET开发,则需要安装特定的应用。由于NET Framework 是仅适用于 Windows 版本的 .NET,所以要进…...

如何把工业通信协议转换成http websocket
1.现状 工业通信协议多数工作在边缘设备上,比如:PLC、IOT盒子等。上层业务系统需要根据不同的工业协议做对应开发,当设备上用的是modbus从站时,采集设备数据需要开发modbus主站;当设备上用的是西门子PN协议时…...
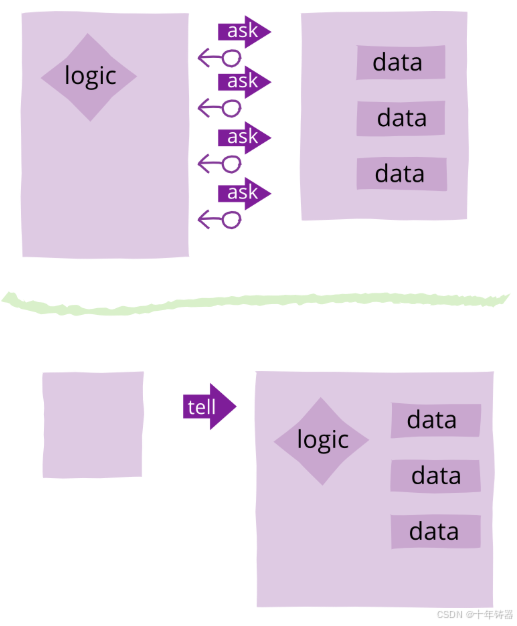
ABAP设计模式之---“Tell, Don’t Ask原则”
“Tell, Don’t Ask”是一种重要的面向对象编程设计原则,它强调的是对象之间如何有效地交流和协作。 1. 什么是 Tell, Don’t Ask 原则? 这个原则的核心思想是: “告诉一个对象该做什么,而不是询问一个对象的状态再对它作出决策。…...
