深度学习 -- pytorch 计算图与动态图机制 autograd与逻辑回归模型
前言
pytorch中的动态图机制是pytorch这门框架的优势所在,阅读本篇博客可以使我们对动态图机制以及静态图机制有更直观的理解,同时在博客的后半部分有关于逻辑回归的知识点,并且使用pytorch中张量以及张量的自动求导进行构建逻辑回归模型。
计算图
计算图是用来描述运算的有向无环图
计算图有两个主要元素:节点(Node)和边(Edge)
节点表示数据,如向量,矩阵,张量,边表示运算,如加减乘除卷积等。
用计算图表示:y = (x+w)*(w+1)
- a = x + w
- b = w + 1
- y = a * b
采用计算图进行计算的好处
它不仅仅能够让我们的运算更加简洁,更重要的作用是使得梯度求导更方便
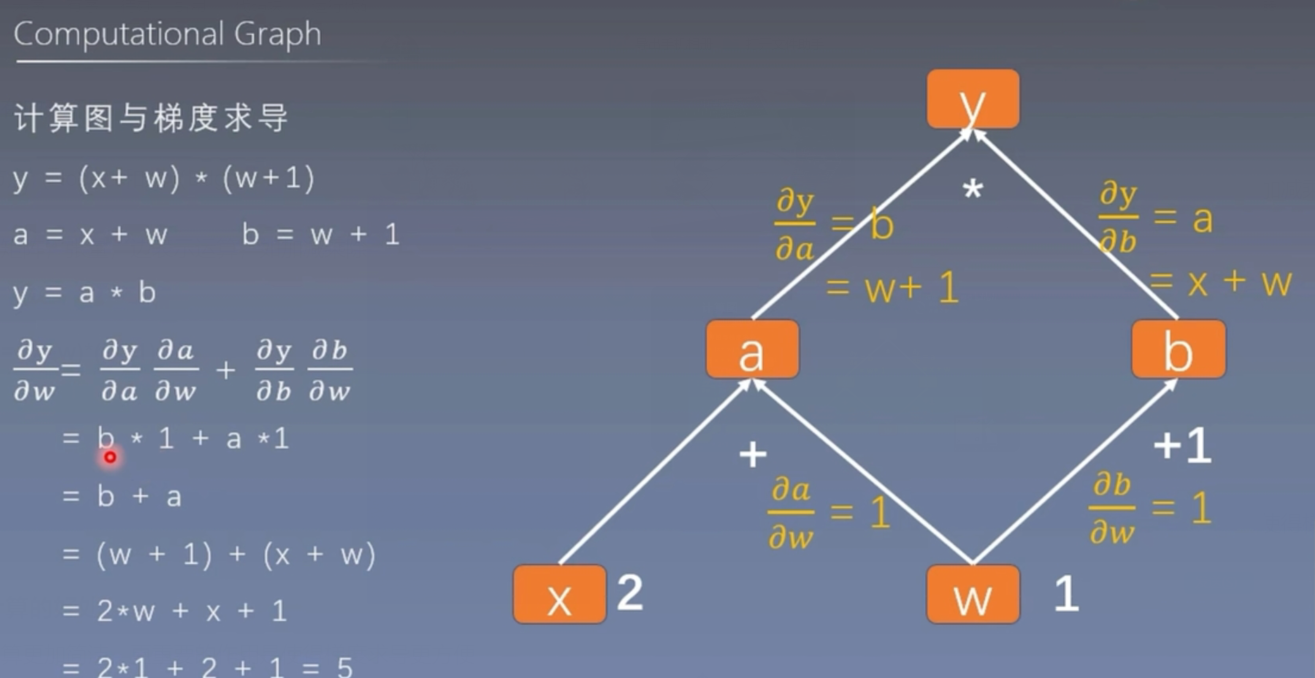
我们可以用pytorch模拟这个过程
import torch# 创建w和x两个节点
w = torch.tensor([1.],requires_grad=True)
x = torch.tensor([2.],requires_grad=True)a = torch.add(w,x)
b = torch.add(w,1)
y = torch.mul(a,b)y.backward() # 调用反向传播 梯度求导
print(w.grad) # tensor([5.])
叶子节点
用户创建的节点称为叶子节点
上述代码创建的w和x 就是叶子节点
is_leaf:知识张量是否为叶子结点
- 只有叶子节点能输出梯度 因为非叶子节点在计算之后的梯度会自动回收
import torch# 创建w和x两个节点
w = torch.tensor([1.],requires_grad=True)
x = torch.tensor([2.],requires_grad=True)a = torch.add(w,x)
b = torch.add(w,1)
y = torch.mul(a,b)# y.backward() # 调用反向传播 梯度求导
# print(w.grad)
print(w.is_leaf,x.is_leaf,a.is_leaf,b.is_leaf,y.is_leaf)
输出:
True True False False False
输出非叶子节点的梯度的方法
在非叶子节点创建之后执行.retain_grad()命令
import torch# 创建w和x两个节点
w = torch.tensor([1.],requires_grad=True)
x = torch.tensor([2.],requires_grad=True)a = torch.add(w,x)
a.retain_grad()
b = torch.add(w,1)
y = torch.mul(a,b)y.backward() # 调用反向传播 梯度求导
# print(w.grad)
# print(w.is_leaf,x.is_leaf,a.is_leaf,b.is_leaf,y.is_leaf)
print(w.grad,a.grad) # tensor([5.]) tensor([2.])
- grad_fn:记录创建该张量时所用的方法
print(y.grad_fn,a.grad_fn,b.grad_fn)
# 输出:
# <MulBackward0 object at 0x0000026458E32CA0>
# <AddBackward0 object at 0x0000026458DA2670>
# <AddBackward0 object at 0x0000026458DA20D0>
动态图与静态图
在计算图中,根据搭建方式的不同,可以将计算图分为动态图和静态图。
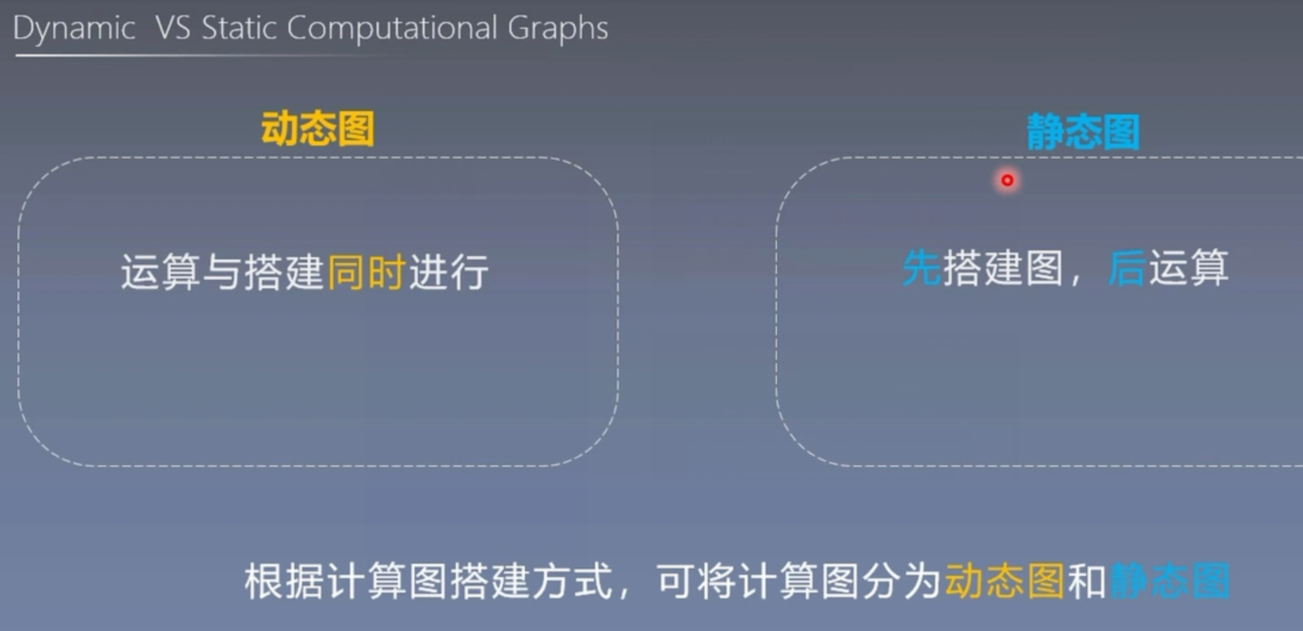
动态图的优点:灵活、易调节
静态图的优点:高效
静态图的缺点:不灵活
pytorch中的自动求导系统autograd
torch.autograd
梯度的计算在模型训练中是十分重要的,然而梯度的计算十分的繁琐,所以pytorch提供了一套自动求导的系统,我们只需要手动搭建计算图,pytorch就能帮我们自动求导。
- torch.autograd.backward
功能:自动求取梯度

tensors:用于求导的张量,如loss
retain_graph:保存计算图
create_graph:创建导数计算图,用于高阶求导
grad_tensors:多梯度权重
张量中的backward()方法实际就是调用了atuograd.backward()方法
y.backward(retain_graph=True)
backward方法中的参数retain_graph,是保存计算图的意思,如果想要连续进行两次反向传播,这个参数必须设置为True,因为如果用默认的false,执行完第一次之后pytorch会把计算图自动释放掉。
grad_tensors的使用
import torch# 创建w和x两个节点
w = torch.tensor([1.],requires_grad=True)
x = torch.tensor([2.],requires_grad=True)a = torch.add(w,x)
a.retain_grad()
b = torch.add(w,1)
y0 = torch.mul(a,b)
y1 = torch.add(a,b)
loss = torch.cat([y0,y1],dim=0)
grad_tensors = torch.tensor([1.,1.])
loss.backward(gradient=grad_tensors)
print(w.grad) # tensor([7.])
- torch.atuograd.grad
功能:求取梯度

outputs:用于求导的张量,如loss
inputs:需要梯度的张量
create_graph:创建导数计算图,用于高阶求导
retain_graph:保存计算图
grad_outputs:多梯度权重
高阶导数
import torch
x = torch.tensor([3.],requires_grad=True)
y = torch.pow(x,2) # y = x**2# 1阶求导 对y进行求导
grad_1 = torch.autograd.grad(y,x,create_graph=True) # create_graph:创建导数计算图,用于高阶求导
print(grad_1) # (tensor([6.], grad_fn=<MulBackward0>),)# 2阶求导
grad_2 = torch.autograd.grad(grad_1[0],x)
print(grad_2) # (tensor([2.]),)
注意:
1、梯度不自动清零
import torch
w = torch.tensor([1.],requires_grad=True)
x = torch.tensor([2.],requires_grad=True)for i in range(4):a = torch.add(w,x)b = torch.add(w,1)y = torch.mul(a,b)y.backward()print(w.grad)输出:
tensor([5.])
tensor([10.])
tensor([15.])
tensor([20.])
说明梯度是不断累加的,原位操作 .grad.zero_() 就能解决这个问题
2、依赖于叶子结点的结点的require_grad都是True
import torch# 创建w和x两个节点
w = torch.tensor([1.],requires_grad=True)
x = torch.tensor([2.],requires_grad=True)a = torch.add(w,x)
a.retain_grad()
b = torch.add(w,1)
y0 = torch.mul(a,b)
y1 = torch.add(a,b)
loss = torch.cat([y0,y1],dim=0)
grad_tensors = torch.tensor([1.,1.])
loss.backward(gradient=grad_tensors)
print(a.requires_grad,b.requires_grad,y0.requires_grad,y1.requires_grad)
# True True True True3、叶子结点不可执行in-place操作(原位操作)
import torch# 创建w和x两个节点
w = torch.tensor([1.],requires_grad=True)
x = torch.tensor([2.],requires_grad=True)a = torch.add(w,x)
a.retain_grad()
b = torch.add(w,1)
y0 = torch.mul(a,b)
y1 = torch.add(a,b)
w.add_(1)
报错信息:
w.add_(1)
RuntimeError: a leaf Variable that requires grad is being used in an in-place operation.
原位操作:在原始地址上直接进行改变
逻辑回归
逻辑回归模型是线性的二分类模型
模型表达式:
y = f(WX + b)
f(x) = 1/(1+e**-x)
f(x) 称为Sigmoid函数,也称为logistic函数
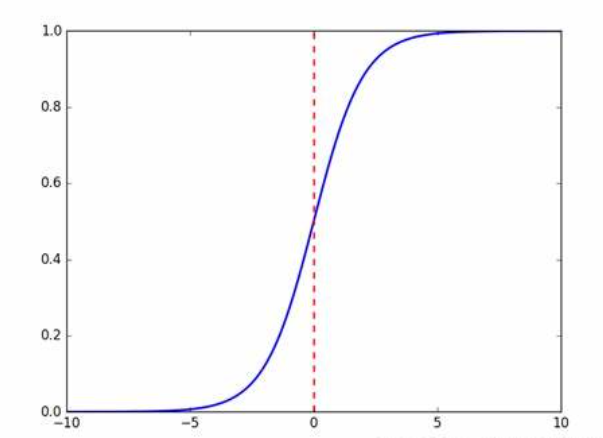
这样的函数我们通过设定一个阈值来进行二分类的工作
比如:当y的值小于等于0>=0.5 则最终输出1,反之则输出0。

线性回归是分析自变量x与因变量y(标量)之间的关系的方法
逻辑回归是分析自变量x与因变量y(概率)之间的关系的方法
pytorch中构建逻辑回归模型
import torch
import torch.nn as nn
import matplotlib.pyplot as plt
import numpy as np# 步骤1 生成数据
sample_nums = 100
mean_value = 1.7
bias = 1
n_data = torch.ones(sample_nums,2)
x0 = torch.normal(mean_value*n_data,1)+bias # 类别0的数据 shape=(100,2)
y0 = torch.zeros(sample_nums) # 类别0的数据 shape=(100,1)
x1 = torch.normal(-mean_value*n_data,1)+bias # 类别1的数据 shape(100,2)
y1 = torch.ones(sample_nums) # 类别为1 标签 shape(100,1)
train_x = torch.cat((x0,x1),0)
train_y = torch.cat((y0,y1),0)# 步骤2 选择模型
class LR(nn.Module):def __init__(self):super(LR,self).__init__()self.features = nn.Linear(2,1)self.sigmoid = nn.Sigmoid()def forward(self,x):x = self.features(x)x = self.sigmoid(x)return xlr_net = LR() # 实例化逻辑回归模型# 步骤3 选择损失函数
loss_fn = nn.BCELoss() # 交叉熵# 步骤4 选择损失函数
lr = 0.01 # 学习率
optimizer = torch.optim.SGD(lr_net.parameters(),lr=lr,momentum=0.9)# 步骤5 模型训练
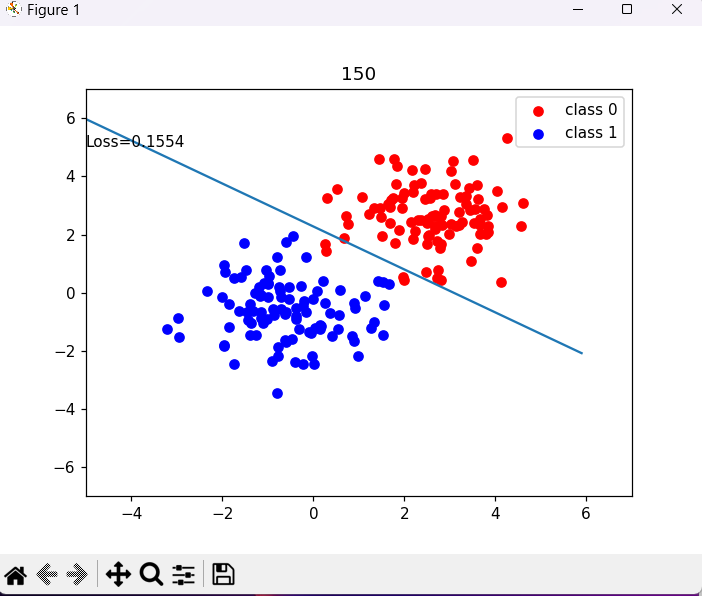
for interation in range(1000):# 前向传播y_pred = lr_net(train_x)# 计算损失loss = loss_fn(y_pred.squeeze(),train_y)# 反向传播loss.backward()# 更新参数optimizer.step()# 绘图if interation % 50==0:mask = y_pred.ge(0.5).float().squeeze() # 以0.5为阈值进行分类correct = (mask == train_y).sum()acc = correct.item()/train_y.size(0)plt.scatter(x0.data.numpy()[:,0],x0.data.numpy()[:,1],c="r",label="class 0")plt.scatter(x1.data.numpy()[:,0],x1.data.numpy()[:,1],c="b",label="class 1")w0,w1 = lr_net.features.weight[0]w0,w1 = float(w0.item()),float(w1.item())plot_b = float(lr_net.features.bias[0].item())plot_x = np.arange(-6,6,0.1)plot_y = (-w0*plot_x - plot_b)/w1plt.xlim(-5,7)plt.ylim(-7,7)plt.plot(plot_x,plot_y)plt.text(-5,5,'Loss=%.4f'%loss.data.numpy())plt.title(interation)plt.legend()plt.show()if acc > 0.99:break
相关文章:

深度学习 -- pytorch 计算图与动态图机制 autograd与逻辑回归模型
前言 pytorch中的动态图机制是pytorch这门框架的优势所在,阅读本篇博客可以使我们对动态图机制以及静态图机制有更直观的理解,同时在博客的后半部分有关于逻辑回归的知识点,并且使用pytorch中张量以及张量的自动求导进行构建逻辑回归模型。 …...
计算机网络学习03(OSI、TCP/IP网络分层模型详解))
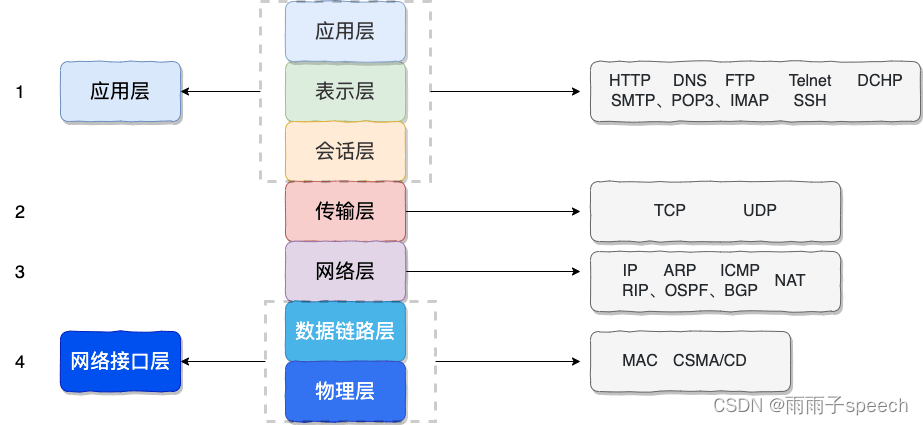
1、OSI 七层模型 OSI 七层模型 是国际标准化组织提出一个网络分层模型,其大体结构以及每一层提供的功能如下图所示: 每一层都专注做一件事情,并且每一层都需要使用下一层提供的功能比如传输层需要使用网络层提供的路由和寻址功能࿰…...

ChatGPT是什么?ChatGPT里的G、P、T分别指什么
文章目录 ChatGPT是什么GTP中的 生成式 是什么意思GTP中的 预训练 是什么意思GTP中的 变换模型 是什么意思 什么是Transformer什么是注意力机制 监督学Xi、无监督学Xi、强化学Xi ChatGPT是什么 GPT: Generative Pre-trained Transformer 生成式预训练变换模型 ChatGPT是由Ope…...
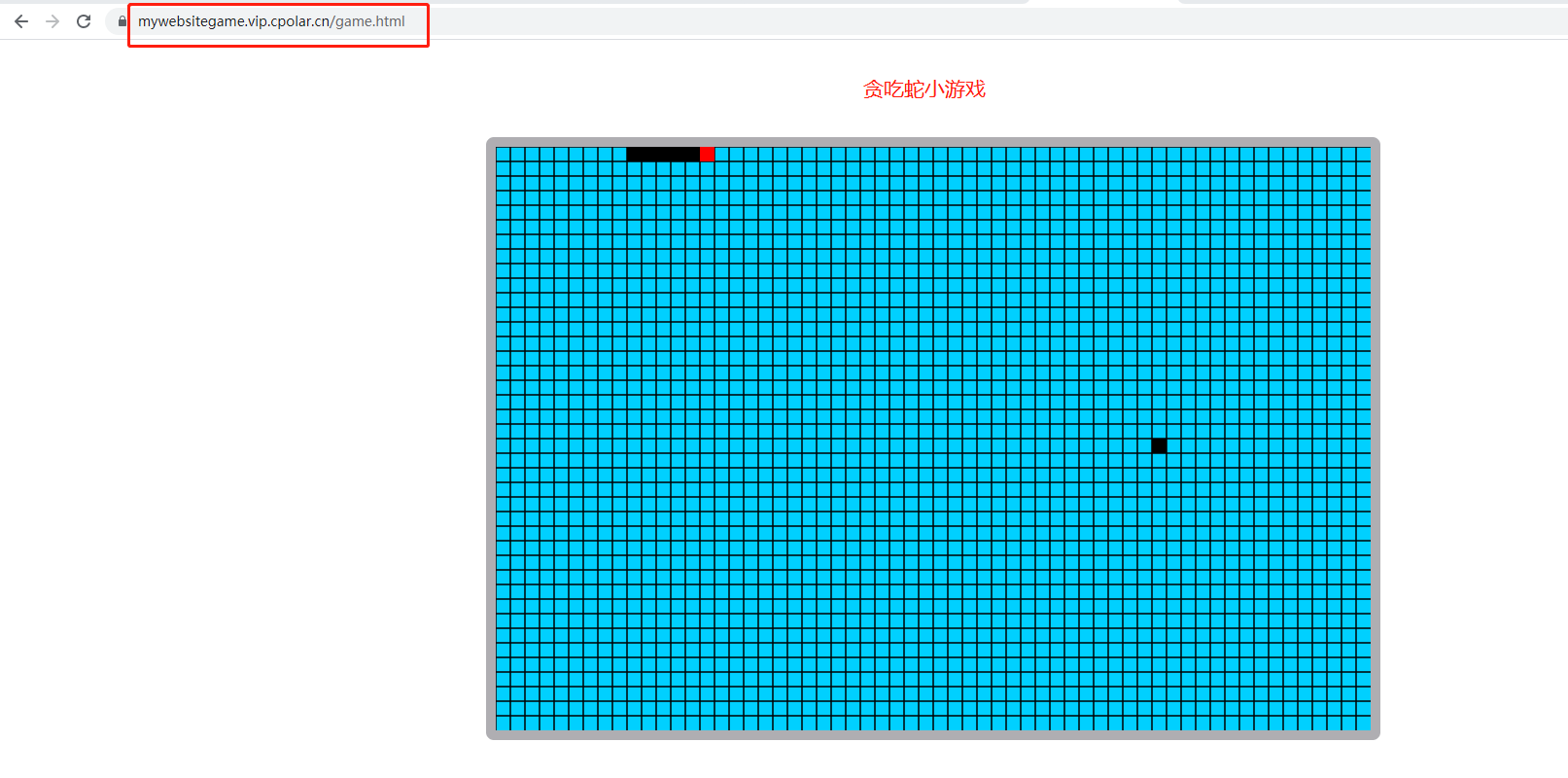
Linux服务使用宝塔面板搭建网站,并发布公网访问 - 内网穿透
文章目录 前言1. 环境安装2. 安装cpolar内网穿透3. 内网穿透4. 固定http地址5. 配置二级子域名6. 创建一个测试页面 转载自远程内网穿透的文章:Linux使用宝塔面板搭建网站,并内网穿透实现公网访问 前言 宝塔面板作为简单好用的服务器运维管理面板&#…...

TDA4VH j784s4 使用
// sdk https://www.ti.com/tool/PROCESSOR-SDK-J784S4 // Jacinto Processors TDA4AP-Q1/TDA4VP-Q1/TDA4AH-Q1/TDA4VH-Q1 EVM User’s Guide https://www.ti.com/lit/ug/spruj62/spruj62.pdf?ts1682337275236&ref_urlhttps%253A%252F%252Fwww.ti.com%252Fsitesearch%252…...
)
CSS布局基础(字体,文本,背景)
字体 常见字体设置 body {font-family: font-family: "Microsoft YaHei", Tahoma, Arial, Hiragino Sans GB,sans-serif; }浏览器从前到后匹配,找到可用字体结束,都没匹配上,使用浏览器默认字体 常用字号 不同浏览器默认字号可…...

Redis入门指南:深入了解这款高性能缓存数据库
本文将带您了解Redis的基本概念、数据类型、特性以及如何在实际项目中应用Redis。通过阅读本文,您将更好地理解如何利用Redis优化您的应用程序性能。 1. 什么是Redis?2. Redis的数据类型3. Redis的特性4. 如何使用Redis4.1 安装与启动4.2 基本命令4.3 应…...

# 数据结构和算法面试题系列-随机算法总结
0 概述 随机算法涉及大量概率论知识,有时候难得去仔细看推导过程,当然能够完全了解推导的过程自然是有好处的,如果不了解推导过程,至少记住结论也是必要的。本文总结最常见的一些随机算法的题目,是几年前找工作的时候…...

windows中vscode配置C/C++环境
首先要把MinGW的环境安装完,我一般是下载带有MinGW的codeblocks,这样省去自己安装MinGW。因为安装MinGW还挺麻烦的。 安装完codeblocks,找到其安装目录,把bin文件配置到环境变量去: 将bin添加到环境变量 然后打开vsco…...
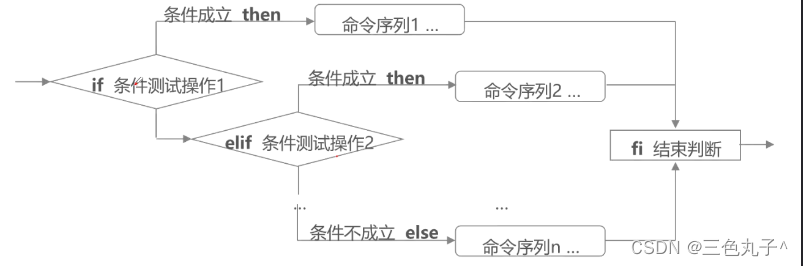
shell编程之条件语句
shell编程之条件语句 一、条件测试操作1.test命令2.文件测试3.利用条件判断,创建文件4.整数值比较4.1 常用的测试操作符 5.字符串比较5.1 常用的测试操作符 6.逻辑测试6.1 常用的测试操作符 二、if语句的结构1.单分支结构2.双分支结构3.多分支结构4.if嵌套 三、case…...

【Python每日十题菜鸟版--第二天】
菜鸟实例 🍉前言1.判断奇偶性2.判断闰年3. 获取最大值最小值4. 质数(素数)的判断5.阶乘方法一方法二 6.九九乘法表7.斐波那契数列方法一 :循环计算法(一般方法)方法二: 递归 8.阿姆斯特朗数9. 十…...
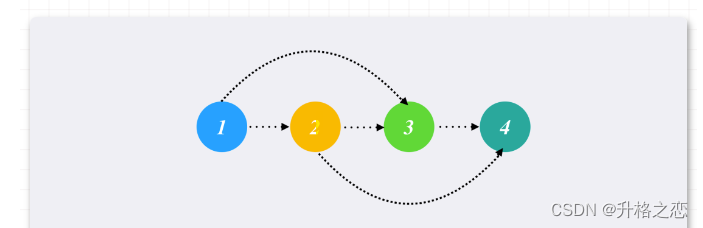
拓扑排序模板及例题
概念 一个有向无环图必然存在一个拓扑序列与之对应。 流程: 先将所有入度为0的节点入队将队列中的节点出队,出队序列就是对应拓扑序。对于弹出的节点x,遍历x所有出度y,对y进行入读减一操作检查入度减一之后的节点y,…...

linux查看nginx安装路径
linux查看nginx安装路径 有几种方法可以查看nginx的安装路径: 使用which命令: which nginx这个命令会返回nginx的二进制文件路径,一般也是安装路径。 查看nginx的进程,得到安装路径: ps aux | grep nginx输出结果中有nginx的进程路径,这个也是安装路径。 在nginx的配置文…...

【生态环境保护】绿水青山就是金山银山——生态环保篇
环保是一个持续性的话题,不仅仅是在国内,整个世界都是一个命运共同体从城市垃圾分类,到农村/村镇污水治理,城乡一体化和因地制宜的实施方式,是我们一直在探索的。 从余村到全国,从中国到世界,“…...
配置Docker镜像加速器-Docker命令-Docker 容器的数据卷
Docker架构 docker进程(daemon) 镜像(Image):Docker 镜像(Image),就相当于是一个 root 文件系统。比如官方镜像 ubuntu:16.04 就包含了完整的一套 Ubuntu16.04 最小系统的 root 文件…...

ARM开发调试方法
用户选用ARM处理器开发嵌入式系统时,选择合适的开发工具可以加快开发进度,节省开发成本。因此一套含有编辑软件、编译软件、汇编软件、链接软件、调试软件、工程管理及函数库的集成开发环境(IDE)一般来说是必不可少的,…...
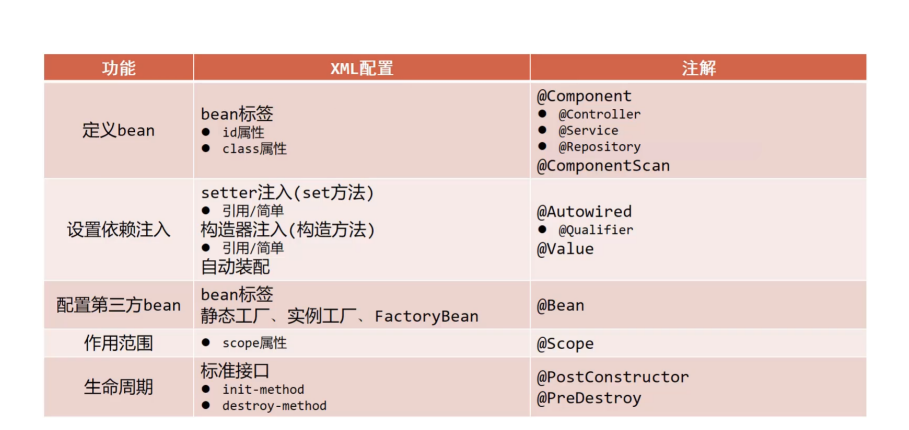
【Spring篇】IOC/DI注解开发
🍓系列专栏:Spring系列专栏 🍉个人主页:个人主页 目录 一、IOC/DI注解开发 1.注解开发定义bean 2.纯注解开发模式 1.思路分析 2.实现步骤 3.注解开发bean作用范围与生命周期管理 1.环境准备 2.Bean的作用范围 3.Bean的生命周期 4.注解开发依赖…...

1 Unix基础知识
1.1 登录 1.1 登录名 登录Unix系统时,要先输入登录名,然后再输入口令。系统再其口令文件(/etc/password文件)查看登录名。口令文件中的登录项由7个以冒号分隔的字段组成:登录名,加密口令,数字用…...

【翻译一下官方文档】认识uniCloud云数据库(基础篇)
我将用图文的形式,把市面上优质的课程加以自己的理解,详细的把:创建一个uniCloud的应用,其中的每一步记录出来,方便大家写项目中,做到哪一步不会了,可以轻松翻看文章进行查阅。(此文…...

全局解释器锁 GIL
问题 你已经听说过全局解释器锁 GIL,担心它会影响到多线程程序的执行性能。 解决方案 尽管 Python 完全支持多线程编程,但是解释器的 C 语言实现部分在完全并行执行时并不是线程安全的。 实际上,解释器被一个全局解释器锁保护着ÿ…...
)
uniapp 对接腾讯云IM群组成员管理(增删改查)
UniApp 实战:腾讯云IM群组成员管理(增删改查) 一、前言 在社交类App开发中,群组成员管理是核心功能之一。本文将基于UniApp框架,结合腾讯云IM SDK,详细讲解如何实现群组成员的增删改查全流程。 权限校验…...

零门槛NAS搭建:WinNAS如何让普通电脑秒变私有云?
一、核心优势:专为Windows用户设计的极简NAS WinNAS由深圳耘想存储科技开发,是一款收费低廉但功能全面的Windows NAS工具,主打“无学习成本部署” 。与其他NAS软件相比,其优势在于: 无需硬件改造:将任意W…...

C++实现分布式网络通信框架RPC(3)--rpc调用端
目录 一、前言 二、UserServiceRpc_Stub 三、 CallMethod方法的重写 头文件 实现 四、rpc调用端的调用 实现 五、 google::protobuf::RpcController *controller 头文件 实现 六、总结 一、前言 在前边的文章中,我们已经大致实现了rpc服务端的各项功能代…...

逻辑回归:给不确定性划界的分类大师
想象你是一名医生。面对患者的检查报告(肿瘤大小、血液指标),你需要做出一个**决定性判断**:恶性还是良性?这种“非黑即白”的抉择,正是**逻辑回归(Logistic Regression)** 的战场&a…...

Java如何权衡是使用无序的数组还是有序的数组
在 Java 中,选择有序数组还是无序数组取决于具体场景的性能需求与操作特点。以下是关键权衡因素及决策指南: ⚖️ 核心权衡维度 维度有序数组无序数组查询性能二分查找 O(log n) ✅线性扫描 O(n) ❌插入/删除需移位维护顺序 O(n) ❌直接操作尾部 O(1) ✅内存开销与无序数组相…...

MVC 数据库
MVC 数据库 引言 在软件开发领域,Model-View-Controller(MVC)是一种流行的软件架构模式,它将应用程序分为三个核心组件:模型(Model)、视图(View)和控制器(Controller)。这种模式有助于提高代码的可维护性和可扩展性。本文将深入探讨MVC架构与数据库之间的关系,以…...

Frozen-Flask :将 Flask 应用“冻结”为静态文件
Frozen-Flask 是一个用于将 Flask 应用“冻结”为静态文件的 Python 扩展。它的核心用途是:将一个 Flask Web 应用生成成纯静态 HTML 文件,从而可以部署到静态网站托管服务上,如 GitHub Pages、Netlify 或任何支持静态文件的网站服务器。 &am…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院查看报告小程序
一、开发环境准备 工具安装: 下载安装DevEco Studio 4.0(支持HarmonyOS 5)配置HarmonyOS SDK 5.0确保Node.js版本≥14 项目初始化: ohpm init harmony/hospital-report-app 二、核心功能模块实现 1. 报告列表…...

解决本地部署 SmolVLM2 大语言模型运行 flash-attn 报错
出现的问题 安装 flash-attn 会一直卡在 build 那一步或者运行报错 解决办法 是因为你安装的 flash-attn 版本没有对应上,所以报错,到 https://github.com/Dao-AILab/flash-attention/releases 下载对应版本,cu、torch、cp 的版本一定要对…...

数据库分批入库
今天在工作中,遇到一个问题,就是分批查询的时候,由于批次过大导致出现了一些问题,一下是问题描述和解决方案: 示例: // 假设已有数据列表 dataList 和 PreparedStatement pstmt int batchSize 1000; // …...
