Python - 数字(Number)数据类型常用操作
目录
- 数字运算
- 类型转换
- 数学函数
- 数学库math、cmath
- math 模块常量
- math 模块方法
- 随机函数库 random
- random 模块方法
- 保留小数到指定位数
- 三角函数
数字运算
=:用于给变量赋值type(x):查看数据所属类型isinstance(x, A_tuple):判断数据是否为预期类型+:两个数相加-:两个数相减*:两个数相乘/:两个数相除%:两个数进行求余**:两个数进行幂运算
# 给变量赋值数字类型数据
int_data = 100 # 整数 int
float_data = 8.88 # 小数 float
complex_data = 3+5j # 复数 complex# 查看变量所属数据类型
print(type(int_data)) # <class 'int'>
print(type(float_data)) # <class 'float'>
print(type(complex_data)) # <class 'complex'># 判断两个数据的类型是否相等
print(isinstance(int_data, int)) # True
print(isinstance(float_data, int)) # False# 加
print(2 + 1) # 3
print(2 + 6.6) # 8.6 整数和浮点数运算结果为浮点数
print(2.1 + 1.2) # 3.3# 减
print(2 - 1) # 1
print(2 - 6.6) # -4.6
print(2.1 - 1.2) # 0.9000000000000001
print(round(2.1 - 1.2, 1)) # 0.9# 乘
print(2 * 1) # 2
print(2 * 6.6) # 13.2
print(2.1 * 1.2) # 2.52# 除
print(2 / 1) # 2.0
print(6.66 / 2) # 3.33
print(6.66 / 2.22) # 3.0# 求余
print(10 % 3) # 1
print(20.22 % 3) # 2.219999999999999# 幂运算
print(5 ** 2) # 5的平方,25
print(2 ** 7) # 2的7次方,128
类型转换
int(x, base=10):将一个字符串或数字转换为整型。x为字符串或数字,base为进制数,默认10进制。float(x):将一个字符串或数字转换为浮点数。x为字符串或整数。
# int()
# 不传参数则为0
int() # 0
# 将字符串转为整数
int("666") # 666
# 向下取整
int(6.66) # 6
# 将数字转为8进制
int('12',8) # 10# flaot()
# 不传参数则为0.0
flaot() # 0.0
# 将字符串转为浮点数
float("6.88") # 6.88
注意:如果转换内容中出现非数字字符则会报错。
数学函数
| 函数 | 说明 |
|---|---|
abs(x) | 返回数字的绝对值。x为数值表达式。 |
max(x) | 返回给定参数的最大值,参数可以为序列。 |
min(x) | 返回给定参数的最小值,参数可以为序列。 |
pow(x, y, z) | 返回x的y次方的值。如果z存在则对结果进行取模,等效于pow(x,y) %z |
round(number, digits) | 返回number保留digits位四舍五入的小数,digits不填默认为保留整数 |
使用示例:
abs(-2.66) # 2.66max(1, 2, 3) # 3
max([6, 7, 8]) # 8min(1, 2, 3) # 1pow(10,2) # 100
pow(10,2,3) # 1round(5.68) # 6
round(5.64, 1) # 5.6
数学库math、cmath
math:模块提供了许多对浮点数的数学运算函数。cmath:模块包含了一些用于复数运算的函数。
查看math中包含的内容:
import mathprint(dir(math))# 打印内容
['__doc__', '__file__', '__loader__', '__name__', '__package__', '__spec__', 'acos', 'acosh', 'asin', 'asinh', 'atan', 'atan2', 'atanh', 'ceil', 'comb', 'copysign', 'cos', 'cosh', 'degrees', 'dist', 'e', 'erf', 'erfc', 'exp', 'expm1', 'fabs', 'factorial', 'floor', 'fmod', 'frexp', 'fsum', 'gamma', 'gcd', 'hypot', 'inf', 'isclose', 'isfinite', 'isinf', 'isnan', 'isqrt', 'ldexp', 'lgamma', 'log', 'log10', 'log1p', 'log2', 'modf', 'nan', 'perm', 'pi', 'pow', 'prod', 'radians', 'remainder', 'sin', 'sinh', 'sqrt', 'tan', 'tanh', 'tau', 'trunc'
]
math 模块常量
| 常量 | 说明 |
|---|---|
math.e | 返回欧拉数 (2.7182…) |
math.inf | 返回正无穷大浮点数 |
math.nan | 返回一个浮点值 NaN (not a number) |
math.pi | π 一般指圆周率。 圆周率 PI (3.1415…) |
math.tau | 数学常数 τ = 6.283185…,精确到可用精度。Tau 是一个圆周常数,等于 2π,圆的周长与半径之比。 |
math 模块方法
| 函数 | 说明 |
|---|---|
math.acos(x) | 返回 x 的反余弦,结果范围在 0 到 pi 之间。 |
math.acosh(x) | 返回 x 的反双曲余弦值。 |
math.asin(x) | 返回 x 的反正弦值,结果范围在 -pi/2 到 pi/2 之间。 |
math.asinh(x) | 返回 x 的反双曲正弦值。 |
math.atan(x) | 返回 x 的反正切值,结果范围在 -pi/2 到 pi/2 之间。 |
math.atan2(y, x) | 返回给定的 X 及 Y 坐标值的反正切值,结果是在 -pi 和 pi 之间。 |
math.atanh(x) | 返回 x 的反双曲正切值。 |
math.ceil(x) | 将 x 向上舍入到最接近的整数 |
math.comb(n, k) | 返回不重复且无顺序地从 n 项中选择 k 项的方式总数。 |
math.copysign(x, y) | 返回一个基于 x 的绝对值和 y 的符号的浮点数。 |
math.cos() | 返回 x 弧度的余弦值。 |
math.cosh(x) | 返回 x 的双曲余弦值。 |
math.degrees(x) | 将角度 x 从弧度转换为度数。 |
math.dist(p, q) | 返回 p 与 q 两点之间的欧几里得距离,以一个坐标序列(或可迭代对象)的形式给出。 两个点必须具有相同的维度。 |
math.erf(x) | 返回一个数的误差函数 |
math.erfc(x) | 返回 x 处的互补误差函数 |
math.exp(x) | 返回 e 的 x 次幂,Ex, 其中 e = 2.718281… 是自然对数的基数。 |
math.expm1() | 返回 Ex - 1, e 的 x 次幂,Ex,其中 e = 2.718281… 是自然对数的基数。这通常比 math.e ** x 或 pow(math.e, x) 更精确。 |
math.fabs(x) | 返回 x 的绝对值。 |
math.factorial(x) | 返回 x 的阶乘。 如果 x 不是整数或为负数时则将引发 ValueError。 |
math.floor() | 将数字向下舍入到最接近的整数 |
math.fmod(x, y) | 返回 x/y 的余数 |
math.frexp(x) | 以 (m, e) 对的形式返回 x 的尾数和指数。 m 是一个浮点数, e 是一个整数,正好是 x == m * 2**e 。 如果 x 为零,则返回 (0.0, 0) ,否则返回 0.5 <= abs(m) < 1 。 |
math.fsum(iterable) | 返回可迭代对象 (元组, 数组, 列表, 等)中的元素总和,是浮点值。 |
math.gamma(x) | 返回 x 处的伽马函数值。 |
math.gcd() | 返回给定的整数参数的最大公约数。 |
math.hypot() | 返回欧几里得范数,sqrt(sum(x**2 for x in coordinates))。 这是从原点到坐标给定点的向量长度。 |
math.isclose(a,b *,rel_tol=1e-09,abs_tol=0.0) | 检查两个值是否彼此接近,若 a 和 b 的值比较接近则返回 True,否则返回 False。 |
math.isfinite(x) | 判断 x 是否有限,如果 x 既不是无穷大也不是 NaN,则返回 True ,否则返回 False 。 |
math.isinf(x) | 判断 x 是否是无穷大,如果 x 是正或负无穷大,则返回 True ,否则返回 False 。 |
math.isnan() | 判断数字是否为 NaN,如果 x 是 NaN(不是数字),则返回 True ,否则返回 False 。 |
math.isqrt() | 将平方根数向下舍入到最接近的整数。 |
math.ldexp(x, i) | 返回 x * (2**i) 。 这基本上是函数 math.frexp() 的反函数。 |
math.lgamma() | 返回伽玛函数在 x 绝对值的自然对数。 |
math.log(x[, base]) | 使用一个参数,返回 x 的自然对数(底为 e )。 |
math.log10(x) | 返回 x 底为 10 的对数。 |
math.log1p(x) | 返回 1+x 的自然对数(以 e 为底)。 |
math.log2(x) | 返回 x 以 2 为底的对数 |
math.perm(n, k=None) | 返回不重复且有顺序地从 n 项中选择 k 项的方式总数。 |
math.pow(x, y) | 将返回 x 的 y 次幂。 |
math.prod(iterable) | 计算可迭代对象中所有元素的积。 |
math.radians(x) | 将角度 x 从度数转换为弧度。 |
math.remainder(x, y) | 返回 IEEE 754 风格的 x 除于 y 的余数。 |
math.sin(x) | 返回 x 弧度的正弦值。 |
math.sinh(x) | 返回 x 的双曲正弦值。 |
math.sqrt(x) | 返回 x 的平方根。 |
math.tan(x) | 返回 x 弧度的正切值。 |
math.tanh(x) | 返回 x 的双曲正切值。 |
math.trunc(x) | 返回 x 截断整数的部分,即返回整数部分,删除小数部分 |
使用示例:
import mathmath.ceil(5.4) # 6
math.ceil(5.5) # 6math.fabs(-6) # 6.0
math.fabs(6) # 6.0math.floor(6.9) # 6math.fmod(5, 2) # 1.0math.isclose(8.005, 8.450, abs_tol = 0.4) # False
math.isclose(8.005, 8.450, abs_tol = 0.5) # True
print(0.1+0.2) # 0.30000000000000004
math.isclose(0.1+0.2, 0.3) #Truemath.isnan(float("NaN")) # Truemath.pow(2, 10) # 1024.0math.sqrt(25) # 5.0
随机函数库 random
查看random中包含的内容:
import randomprint(dir(random))# 打印内容
['BPF', 'LOG4', 'NV_MAGICCONST', 'RECIP_BPF', 'Random', 'SG_MAGICCONST', 'SystemRandom', 'TWOPI', '_Sequence', '_Set', '__all__', '__builtins__', '__cached__', '__doc__', '__file__', '__loader__', '__name__', '__package__', '__spec__', '_accumulate', '_acos', '_bisect', '_ceil', '_cos', '_e', '_exp', '_inst', '_log', '_os', '_pi', '_random', '_repeat', '_sha512', '_sin', '_sqrt', '_test', '_test_generator', '_urandom', '_warn', 'betavariate', 'choice', 'choices', 'expovariate', 'gammavariate', 'gauss', 'getrandbits', 'getstate', 'lognormvariate', 'normalvariate', 'paretovariate', 'randint', 'random', 'randrange', 'sample', 'seed', 'setstate', 'shuffle', 'triangular', 'uniform', 'vonmisesvariate', 'weibullvariate'
]
random 模块方法
| 函数 | 说明 |
|---|---|
seed() | 初始化随机数生成器。 |
getstate() | 返回捕获生成器当前内部状态的对象。 |
setstate() | state 应该是从之前调用 getstate() 获得的,并且 setstate() 将生成器的内部状态恢复到 getstate() 被调用时的状态。 |
getrandbits(k) | 返回具有 k 个随机比特位的非负 Python 整数。 此方法随 MersenneTwister 生成器一起提供,其他一些生成器也可能将其作为 API 的可选部分提供。 在可能的情况下,getrandbits() 会启用 randrange() 来处理任意大的区间。 |
randrange() | 从 range(start, stop, step) 返回一个随机选择的元素。 |
randint(a, b) | 返回随机整数 N 满足 a <= N <= b。 |
choice(seq) | 从非空序列 seq 返回一个随机元素。 如果 seq 为空,则引发 IndexError。 |
choices(population, weights=None, *, cum_weights=None, k=1) | 从 population 中选择替换,返回大小为 k 的元素列表。 如果 population 为空,则引发 IndexError。 |
shuffle(x[, random]) | 将序列 x 随机打乱位置。 |
sample(population, k, *, counts=None) | 返回从总体序列或集合中选择的唯一元素的 k 长度列表。 用于无重复的随机抽样。 |
random() | 返回 [0.0, 1.0) 范围内的下一个随机浮点数。 |
uniform(x, y) | 随机生成下一个实数,它在[x,y]范围内。 |
triangular(low, high, mode) | 返回一个随机浮点数 N ,使得 low <= N <= high 并在这些边界之间使用指定的 mode 。 low 和 high 边界默认为零和一。 mode 参数默认为边界之间的中点,给出对称分布。 |
betavariate(alpha, beta) | Beta 分布。 参数的条件是 alpha > 0 和 beta > 0。 返回值的范围介于 0 和 1 之间。 |
expovariate(lambd) | 指数分布。 lambd 是 1.0 除以所需的平均值,它应该是非零的。 |
gammavariate() | Gamma 分布( 不是伽马函数) 参数的条件是 alpha > 0 和 beta > 0。 |
gauss(mu, sigma) | Gamma 分布( 不是伽马函数) 参数的条件是 alpha > 0 和 beta > 0。 |
lognormvariate(mu, sigma) | 对数正态分布。 如果你采用这个分布的自然对数,你将得到一个正态分布,平均值为 mu 和标准差为 sigma 。 mu 可以是任何值,sigma 必须大于零。 |
normalvariate(mu, sigma) | 正态分布。 mu 是平均值,sigma 是标准差。 |
vonmisesvariate(mu, kappa) | 冯·米塞斯分布。 mu 是平均角度,以弧度表示,介于0和 2*pi 之间,kappa 是浓度参数,必须大于或等于零。 |
paretovariate(alpha) | 帕累托分布。 alpha 是形状参数。 |
weibullvariate(alpha, beta) | 威布尔分布。 alpha 是比例参数,beta 是形状参数。 |
使用示例:
import random# 从1-100中选一个整数
print(random.randint(1,100)) # 80print(random.choice([1, 2, 3, 5, 9])) # 2
print(random.choice('A String')) # A
print(random.choice(range(10))) # 8# 从 1-100 中选取一个奇数
print(random.randrange(1, 100, 2)) # 57
# 从 0-99 选取一个随机数
print(random.randrange(100)) # 91
# 随机选取0到100间的偶数
print(random.randrange(0, 101, 2)) # 22print(random.random()) # 0.699045676948276print(random.uniform(1, 100)) # 66.79353123577998
保留小数到指定位数
# 向下取整,转为整数
print(int(58.86)) # 58import math
# 向上取整,转为整数
print(math.ceil(58.86)) # 59# 四舍五入,转为整数
print(round(58.86)) # 59# 四舍五入,保留2位小数
print(round(4.859999999999999, 2)) # 4.86# 分割整数和小数
print(str(58.866).split(".")[0]) # 58
三角函数
| 函数 | 说明 |
|---|---|
acos(x) | 返回x的反余弦弧度值。 |
asin(x) | 返回x的反正弦弧度值。 |
atan(x) | 返回x的反正切弧度值。 |
atan2(y, x) | 返回给定的 X 及 Y 坐标值的反正切值。 |
cos(x) | 返回x的弧度的余弦值。 |
hypot(x, y) | 返回欧几里德范数 sqrt(xx + yy)。 |
sin(x) | 返回的x弧度的正弦值。 |
tan(x) | 返回x弧度的正切值。 |
degrees(x) | 将弧度转换为角度,如degrees(math.pi/2) , 返回90.0。 |
radians(x) | 将角度转换为弧度。 |
相关文章:
数据类型常用操作)
Python - 数字(Number)数据类型常用操作
目录数字运算类型转换数学函数数学库math、cmathmath 模块常量math 模块方法随机函数库 randomrandom 模块方法保留小数到指定位数三角函数数字运算 :用于给变量赋值type(x):查看数据所属类型isinstance(x, A_tuple):判断数据是否为预期类型…...
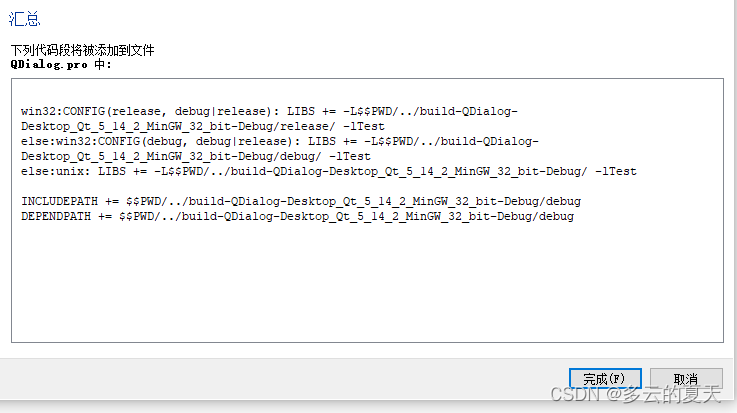
QT(51)-动态链接库-windows
1.qt- 调用win32 DLL 2.qt- 调用MFC DLL 0概述: 01.扩展DLL: 必须有一个DllMain()函数,且调用AfxInitExtensionModule()函数。 CRuntimeClass类-初始化函数CDynLinkLibrary。02.windows定位DLL文件: 1)…...
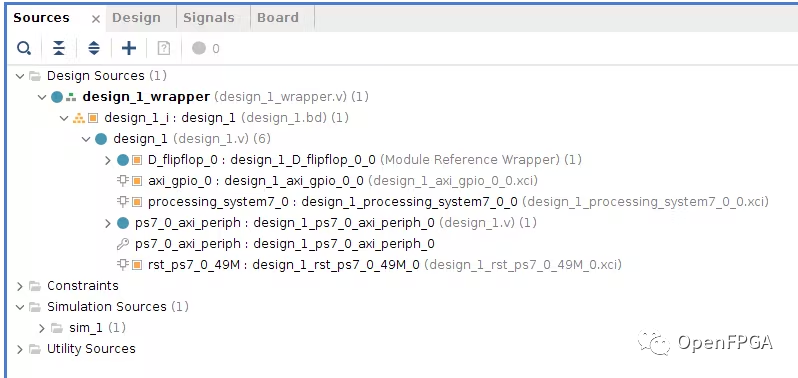
[Vivado那些事儿]将自定义 IP (HDL)添加到 Vivado 模块设计(Block Design)
绪论使用Vivado Block Design设计解决了项目继承性问题,但是还有个问题,不知道大家有没有遇到,就是新设计的自定义 RTL 文件无法快速的添加到Block Design中,一种方式是通过自定义IP,但是一旦设计的文件有问题就需要重…...

开学必备数码清单,大学生开学必备数码好物分享
还有很多小伙伴不知道开学应该准备什么,在学校当中需要用到的数码产品,在宿舍娱乐使用的音箱、学习当中使用到的笔记本,这些都是我们可以准备的,还有一个小众的好物,能够让我们在学校当中提升生活的幸福感,…...

【面试题】常见前端基础面试题(HTML,CSS,JS)
大厂面试题分享 面试题库后端面试题库 (面试必备) 推荐:★★★★★地址:前端面试题库html语义化的理解代码结构: 使页面在没有css的情况下,也能够呈现出好的内容结构有利于SEO: 爬虫根据标签来分配关键字的权重,因此可以和搜索引擎…...
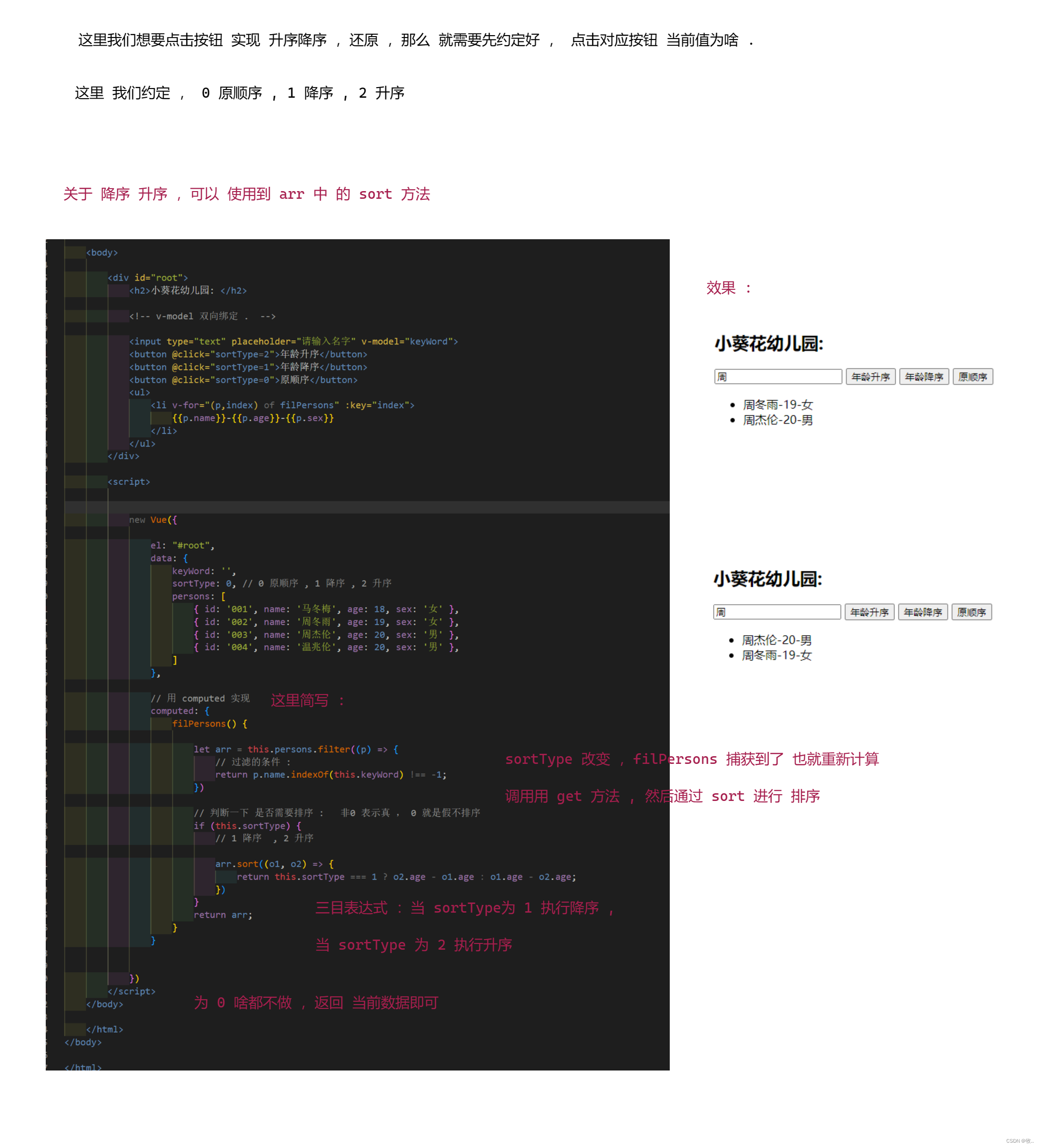
Vue (4)
文章目录1. 绑定样式1.1 绑定 class 样式1.2 绑定 style 样式2. 条件渲染2.1 v-show2.2 v-if3. 列表渲染3.1 v-for3.2 key 的作用与原理3.3 列表过滤3.4 列表排序1. 绑定样式 说 绑定样式 前,先准备好 以下几个 样式 : <style>.basic {width: 400px;height: 1…...
静态库和动态库的制作
一、什么叫做库: 库:二进制的程序,能被操作系统载入内存中执行 二、Linux下的库有两种:静态库和共享库(动态库),二者的不同点在于代码载入的时刻不同。 A、静态库在程序编译的时候并会被连接到目标代码中,程…...
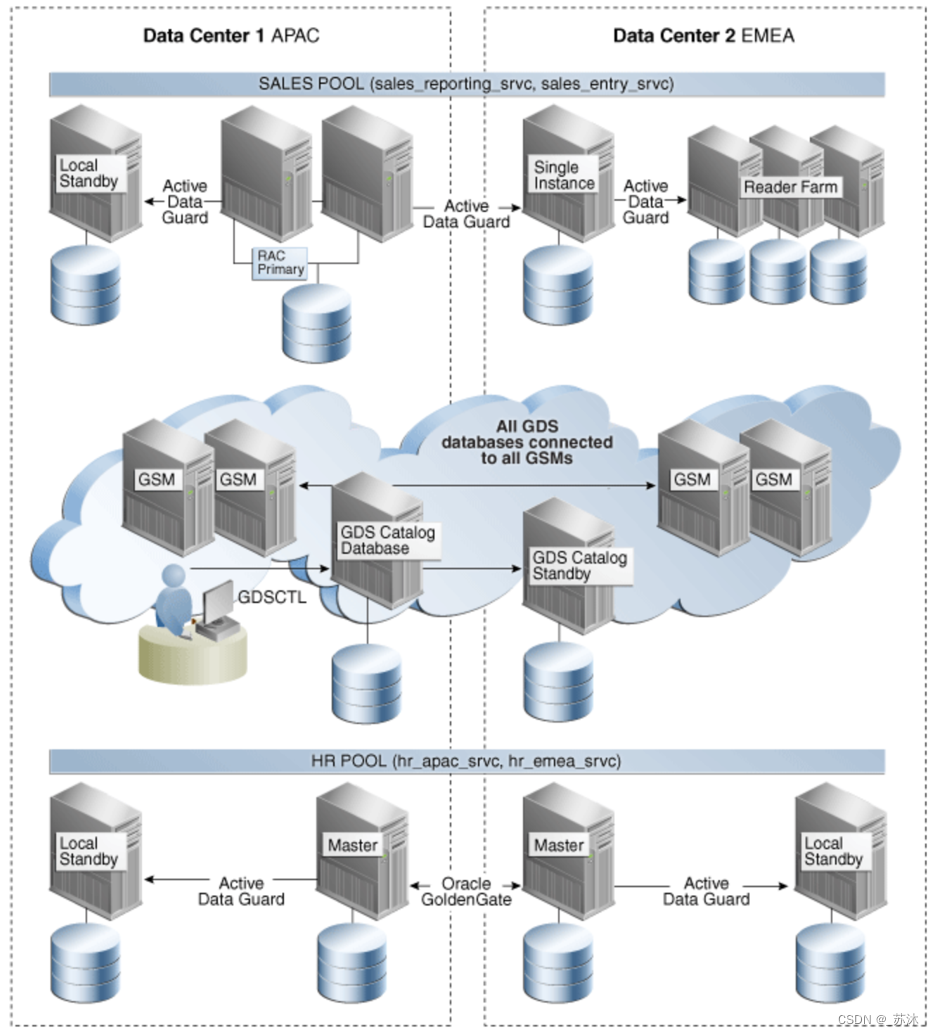
Oracle实现高可用性的工具(负载均衡/故障切换)
Oracle实现高可用性的工具(负载均衡/故障切换)1 Oracle RAC故障转移负载均衡2 Data Guard负载均衡-读写分离Data Guard Broker3 GDSGSM:连接管理工具主要功能Data Guard Broker功能是监控Data Guard状态,当主库异常时自动切换角色…...
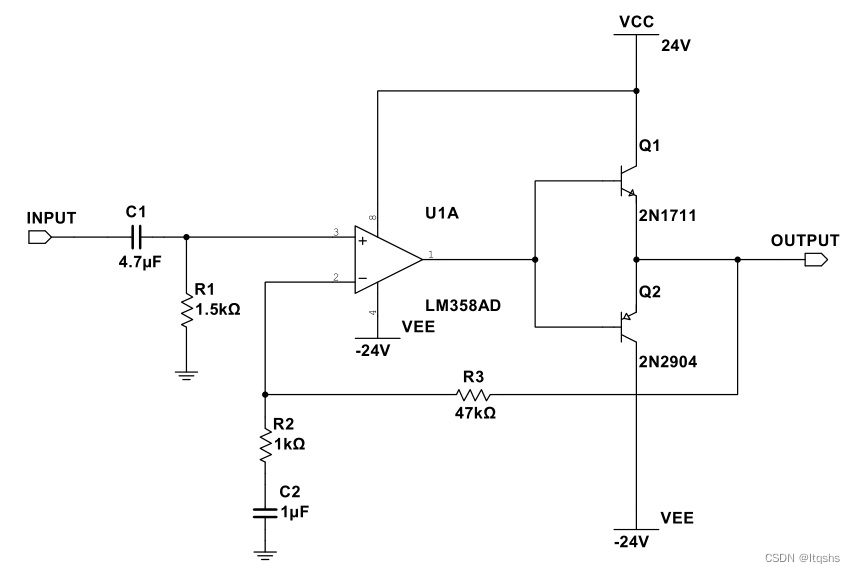
图解经典电路之OCL差分功放-三极管分立器件电路分析
下面从简到繁,从框架到细节的顺序讲解电路。即先讲框架,然后逐渐添加电路细节,所以大家跟上思路。 1、第一步,尽可能的抽象这个电路,等效如下: 图二 OCL等效电路 整个OCL电路,可以等效为一个大功率的运放,加上几个电阻电容构成了一个同向放大器,就是这么简单。 为了便…...

thymeleaf模板注入学习与研究--查找与防御
一、日常编码中常见的两种漏洞场景 1.1 模板参数外部可控 RequestMapping("/path")public String path(RequestParam String lang) {return lang ;}实际开发过程中 依靠我丰富的想象力只能想出 换主题 这种场景下可能会出现 大佬们自行脑补吧。 1.2 使用GetMappin…...
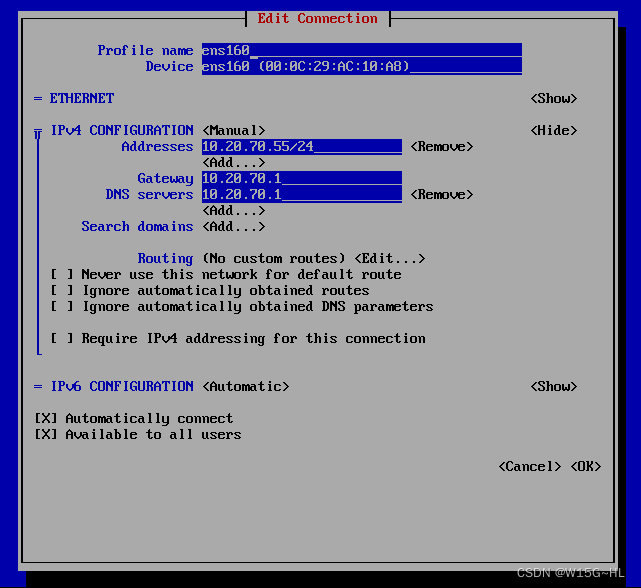
第七章:Linux最小化搭建环境解说2
配置IP地址:我们先要到网卡配置文件夹里,路径是/etc/sysconfig/network-scripts/,有点长,不过没事,我们要学会习惯,这还是经常用的。然后就是用ls命令查看下面有什么,只有一个文件ifcfg-ens160&…...

两道链表经典算法题---链表有无环(基础+进阶)
生活就像一盒巧克力,你永远不知道你会得到什么。——《阿甘正传》目前自己粗略的学完数据结构,正在开始刷算法题目。个人觉得算法是一个积累,循序渐进的的过程,需要不断加量,进而达到所谓的质。链表作为数据结构一个重…...

2023/1/14总结
今天学习的是c语法知识。 容器arry: 通俗来说这个容器就i是c语言的数组,和C中vevtor不同,arry是定长度的,而vector是动态数组。头文件为:<arry> 初始化: arry<数据类型,你所要声明…...

Python 之 NumPy 统计函数、数据类型和文件操作
文章目录一、统计函数1. 求平均值 mean()2. 中位数 np.median3. 标准差 ndarray.std4. 方差 ndarray.var()5. 最大值 ndarray.max()6. 最小值 ndarray.min()7. 求和 ndarray.sum()8. 加权平均值 numpy.average()二、数据类型1. 数据存储2. 定义结构化数据3. 结构化数据操作三、…...
互联网新时代要到来了(一)什么是Web3.0?
什么是Web3.0? tips:内容来自百度百科、知乎、搜狐新闻、李留白公众号、CSDN「Meta.Qing」博客等网页 什么是Web3.0?1.什么是Web3.0(概念介绍)?2.Web3.0简单理解3.Web3.0的技术特点4.Web3.0项目1.什么是Web3.0(概念…...

[Yocto] 直接向deploy/images目录部署binary
最近用yocto的时候碰到一个问题,有一些IP的FW binary是从别的地方直接拿来的,没有source code,有一个需求就是需要把它用wks script的方式把它们打包到最后的image里,这篇文章就是来谈谈这个问题。 yocto patch/deploy等做了什么 首先,虽然我们的code,bbfile,或者说pa…...
设备控制开发与实现(二))
HarmonyOS Connect原子化服务功能开发(Wi-Fi/Combo)设备控制开发与实现(二)
规设备控制 在“device”目录下的“DeviceApplication.java”文件中,在onInitialize函数中初始化应用。示例代码如下: Override public void onInitialize() {AiLifeServiceHelper.initApplication(this);DeviceHandlerAbility.register(this, "&qu…...

浅析 Makefile
Makefile逻辑 Makefile就是将一系列的工作流串在一起自动执行,构成Makefile最基本的要素是目标、依赖、命令。也就是为了实现目标需要哪些依赖并执行什么样的命令。 target: dependences1 dependences2 ... command1 command2 ...其中,target表示要生…...

保护品牌线上声誉的5种方法
我们如今生活在一个搜索便捷的世界,对于一个企业和个人来说,品牌的线上声誉也尤为重要。在客户考虑与您的公司开展业务之前,他们理所当然会先使用众多软件和平台搜索相关信息,以帮助他们了解和做决定。 因此,您的品牌…...

Java多重选择结构,超详细整理,适合新手入门
目录 一、什么是多重选择结构? 二、if 语句的语法 1、什么是嵌套if语句? 2、if 语句循环基本用法: 3、案例: 二、if...else多重选择结构语法 1、什么是if-else语句? 2、if...else 循环基本用法 3、案例&#…...

Vue记事本应用实现教程
文章目录 1. 项目介绍2. 开发环境准备3. 设计应用界面4. 创建Vue实例和数据模型5. 实现记事本功能5.1 添加新记事项5.2 删除记事项5.3 清空所有记事 6. 添加样式7. 功能扩展:显示创建时间8. 功能扩展:记事项搜索9. 完整代码10. Vue知识点解析10.1 数据绑…...

【Linux】shell脚本忽略错误继续执行
在 shell 脚本中,可以使用 set -e 命令来设置脚本在遇到错误时退出执行。如果你希望脚本忽略错误并继续执行,可以在脚本开头添加 set e 命令来取消该设置。 举例1 #!/bin/bash# 取消 set -e 的设置 set e# 执行命令,并忽略错误 rm somefile…...

调用支付宝接口响应40004 SYSTEM_ERROR问题排查
在对接支付宝API的时候,遇到了一些问题,记录一下排查过程。 Body:{"datadigital_fincloud_generalsaas_face_certify_initialize_response":{"msg":"Business Failed","code":"40004","sub_msg…...
)
IGP(Interior Gateway Protocol,内部网关协议)
IGP(Interior Gateway Protocol,内部网关协议) 是一种用于在一个自治系统(AS)内部传递路由信息的路由协议,主要用于在一个组织或机构的内部网络中决定数据包的最佳路径。与用于自治系统之间通信的 EGP&…...

spring:实例工厂方法获取bean
spring处理使用静态工厂方法获取bean实例,也可以通过实例工厂方法获取bean实例。 实例工厂方法步骤如下: 定义实例工厂类(Java代码),定义实例工厂(xml),定义调用实例工厂ÿ…...

sqlserver 根据指定字符 解析拼接字符串
DECLARE LotNo NVARCHAR(50)A,B,C DECLARE xml XML ( SELECT <x> REPLACE(LotNo, ,, </x><x>) </x> ) DECLARE ErrorCode NVARCHAR(50) -- 提取 XML 中的值 SELECT value x.value(., VARCHAR(MAX))…...

NPOI Excel用OLE对象的形式插入文件附件以及插入图片
static void Main(string[] args) {XlsWithObjData();Console.WriteLine("输出完成"); }static void XlsWithObjData() {// 创建工作簿和单元格,只有HSSFWorkbook,XSSFWorkbook不可以HSSFWorkbook workbook new HSSFWorkbook();HSSFSheet sheet (HSSFSheet)workboo…...

django blank 与 null的区别
1.blank blank控制表单验证时是否允许字段为空 2.null null控制数据库层面是否为空 但是,要注意以下几点: Django的表单验证与null无关:null参数控制的是数据库层面字段是否可以为NULL,而blank参数控制的是Django表单验证时字…...

消息队列系统设计与实践全解析
文章目录 🚀 消息队列系统设计与实践全解析🔍 一、消息队列选型1.1 业务场景匹配矩阵1.2 吞吐量/延迟/可靠性权衡💡 权衡决策框架 1.3 运维复杂度评估🔧 运维成本降低策略 🏗️ 二、典型架构设计2.1 分布式事务最终一致…...
:电商转化率优化与网站性能的底层逻辑)
精益数据分析(98/126):电商转化率优化与网站性能的底层逻辑
精益数据分析(98/126):电商转化率优化与网站性能的底层逻辑 在电子商务领域,转化率与网站性能是决定商业成败的核心指标。今天,我们将深入解析不同类型电商平台的转化率基准,探讨页面加载速度对用户行为的…...
