数据结构初阶 —— 树(堆)
目录
一,堆
堆的概念
向下调整法(数组)
向上调整法(数组)
堆的创建(建堆)
堆的实现
一,堆
堆的概念
- 如有个关键码的集合K={
,
,
,...,
},把它的所有元素按完全二叉树的顺序存储方式存储在一个一维数组中,并满足
<=
且
<=
(
>=
且
>=
),i=0、1、...,则称为小堆(大堆);
小堆
<=
且
<=
,即所有节点小于等于孩子;
- 根节点最小,叫做最小堆或小根堆;
大堆
>=
且
>=
,即所有节点大于等于孩子;
- 根节点最大,叫做最大堆或大根堆;
堆的性质
- 堆中某个节点的值,总是不大于或不小于其父节点的值;
- 根一定是最值(最大值或最小值);
- 堆总是一颗完全二叉树,适合顺序结构存储;
向下调整法(数组)
- 将数组看做为一颗完全二叉树,可使用向下调整法创建堆;
- 前提条件为,此二叉树的左右子树需是一个堆,只有根节点不满足堆要求;
- 从根开始,与左右子节点中的最小值,比较并交换,依次类推,直到比父亲大或到叶子节点终止;
- 时间复杂度,O(logN);
- 注,向上调整法类似;
int array[] = {27,15,19,18,28,34,65,49,25,37};

//向下调整法,小堆
void Swap(int* px, int* py)
{int tmp = *px;*px = *py;*py = tmp;
}void AdjustDown(int* arr, int n, int parent)
{int child = 2 * parent + 1;//无孩子节点或父亲小于孩子,即终止while (child < n){if (child + 1 < n && arr[child + 1] < arr[child])child++;if (arr[parent] > arr[child]){Swap(arr + parent, arr + child);parent = child;child = 2 * parent + 1;}elsebreak;}
}向上调整法(数组)
//向上调整法
void AdjustUp(int* arr, int child)
{int parent = (child - 1) / 2;//大堆//根节点或父亲大于孩子,即终止while (child > 0){if (arr[parent] < arr[child]){Swap(arr + parent, arr + child);child = parent;parent = (child - 1) / 2;}elsebreak;}
}堆的创建(建堆)
- 即对数据如数组(可看为完全二叉树),将其构建为堆;
- 方法为,从倒数第一个非叶子节点的子树开始调整,直到根节点为止;
- 即每次调整时,使用向下调整法;
- 建堆时间复杂度,O(N),下面有证明;
- 注,也可使用向上调整法建堆,但初始化堆的个别元素位置可能不一样;
int arr[] = {1,5,3,8,7,6}; //建堆-向下调整法
void Heap(int* arr, int n)
{int i = (n - 1 - 1) / 2; //最后节点的父节点for (i; i >= 0; i--){AdjustDown(arr, n, i);}
}//建堆-向上调整法
void Heap(int* arr, int n)
{int i = 1; for (i; i < n; i++){AdjustUp(arr, i);}
}
建堆时间复杂度


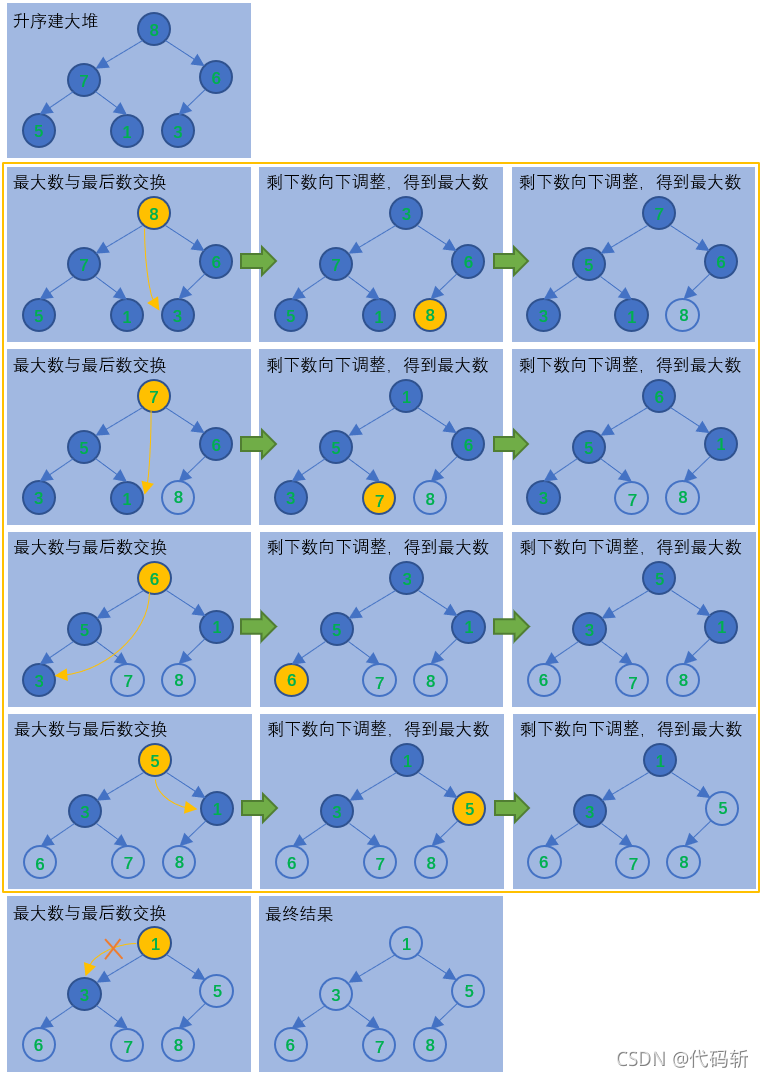
堆排序
- 升序,建大堆(将最大的数换到最后,在将剩下的数向下调整下,选出次大数,依次类推);
- 降序,建小堆(将最小的数换到最后,在将剩下的数向下调整下,选出次小数,依次类推);
- 整体的时间复杂度,O(N*logN);
- 如升序建小堆(或降序建大堆)的话,选出最值后,需在继续建堆(O(N)),效率较低,还不如直接遍历,建堆的价值未体现;
//建堆排序
void HeapSort(int* arr, int n)
{//建堆 - O(N)int i = (n - 1 - 1) / 2; //最后节点的父节点for (i; i >= 0; i--){AdjustDown(arr, n, i);}//排序 - O(N*log(N))int end = n - 1;while (end){Swap(arr, arr + end);AdjustDown(arr, end, 0);end--;}
}
堆的实现
//堆
typedef int HPDataType;typedef struct Heap
{HPDataType* data;int size;int capacity;
}Heap;//初始化
void HeapInit(Heap* php, HPDataType* arr, int n);//释放销毁
void HeapDestroy(Heap* php);//插入数据并保持堆
void HeapPush(Heap* php, HPDataType* x);//删除堆顶数据并保持堆
void HeapPop(Heap* php);//返回堆顶数据
HPDataType HeapTOP(Heap* php);//返回堆节点个数
int HeapSize(Heap* php);//判断释放为空
bool HeapEmpty(Heap* php);
注:完整接口实现代码路径https://gitee.com/napoleoncode/start-code/tree/master/%E6%95%B0%E6%8D%AE%E7%BB%93%E6%9E%84/06_Heap
TOP-K问题
- 直接排序,O(N*log(N));
- 建个N个数的堆,并取出前K个数,O(N+K*log(N));
- 建个K个数的小堆,然后将剩下的数依次与堆顶比较,大即入堆,最后此堆即为最大的K个数,O(N*log(K));(如N非常大内存不够,前两种方法即适用了);
- 注,通常K远小于N;
//TOP-K
void TOPK(int* arr, int n, int k)
{Heap hp;//建堆HeapInit(&hp, arr, k);int i = k;for (i; i < n; i++){//替换if (HeapTop(&hp) > arr[i]){HeapPop(&hp);HeapPush(&hp, arr[i]);}}HeapPrint(&hp);HeapDestroy(&hp);
}相关文章:

数据结构初阶 —— 树(堆)
目录 一,堆 堆的概念 向下调整法(数组) 向上调整法(数组) 堆的创建(建堆) 堆的实现 一,堆 堆的概念 如有个关键码的集合K{,,,...…...

一文看懂低代码,5分钟从入门到原理全搞定
全球低代码市场已经走过了近20年,中国低代码市场近5年经历了百花齐放的广泛探索阶段,更旺盛的市场需求逐步在被激发。现在,让我们按下暂停键,看看这些产品给我们呈现了低代码市场一幅怎样的百景图。 低代码平台简介 广义上的低代…...
MetaERP系统主要干什么的,华为自研ERP的路子是否可以效仿?
近日,华为成功研发出自主可控的MetaERP系统,并完成了对旧有ERP系统的替换。该系统采用全栈自主可控技术,基于华为欧拉操作系统、GaussDB等根技术,采用云原生架构、元数据多租架构、实时智能技术等,提高业务效率&#x…...

自动驾驶——离散LQR的黎卡提方程Riccati公式推导与LQR工程化
1.LQR Question Background 之前写过连续系统的黎卡提方程Riccati推导,但是考虑到实际工程落地使用的是离散系统,于是又进行了离散黎卡提方程Riccati的公式推导。 2.Proof of Riccati Equation Formula for Discrete Systems 工程化落地,就…...
28.Mybatis的入门
目录 一、Mybatis的入门。 (1)Mybatis的简介。 (2)Mybatis的快速入门。 (2.1)快速入门。 (2.2)UserMapper.xml文件。 (2.3)sqlMapConfig.xml文件。 …...
)
Android Jetpack 从使用到源码深耕【ViewModel从实践到原理 】(三)
上文,我们通过简单的ViewModel使用源码入手,对其源码进行阅读,原理进行了简单总结,简单来说,ViewModel是通过Activity的onRetainNonConfigurationInstance 与 getLastNonConfigurationInstance的自动调用,实现了 ViewModel数据的存储和恢复,数据存储在ViewModelStore的m…...

什么性格的人适合报考环境科学类专业?高考选专业
环境科学类专业包括有:环境科学与工程,环境工程,环境科学,环境生态工程,环保设备工程,资源环境科学,水质科学与技术。 环境对于未来是一个极其重要的方向,需要学生具备一定的科学素…...

Python中的异常处理机制可以帮助程序员在程序运行过程中遇到错误时进行处理
Python中的异常处理机制可以帮助程序员在程序运行过程中遇到错误时进行处理,防止程序崩溃或出现不可预测的错误。 Python中的异常处理使用try-except语句。try语句块包含可能会出现异常的代码,而except语句块则定义了出现异常时应该执行的操作。下面是一…...

TCP之报文格式解析
TCP网络协议是较常用的,也基本上都会接触,那么来简单了解下它吧。TCP 是一种面向连接的、可靠的传输协议,它能够将数据分成一些小块,并通过 Internet 进行传输。在 TCP 中,数据被分割成一些称为 TCP 报文段(…...
——裸机 arm 程序环境搭建)
qemu-基础篇(二)——裸机 arm 程序环境搭建
文章目录 测试代码makefile运行 qemu调试 qemuGDB 常用命令 裸机篇系列文章主要用于熟悉 arm 汇编及处理器结构 测试代码 _start:ldr r0, 0X020C4068 /* CCGR0 */ldr r1, 0XFFFFFFFF str r1, [r0]ldr r0, 0X020C406C /* CCGR1 */str r1, [r0]ldr r0, 0X020C4070 …...
)
JSP+SQL基于JSP的学生信息管理系统(源代码+论文+答辩PPT)
随着学校规模的不断扩大,学生数量急剧增加,有关学生的各种信息也成倍增长。面对如此庞大的信息量,开发学生信息管理系统来提高学生管理工作的效率就成为必然。通过该系统,可以做到信息的规范管理、科学统计和快速查询,…...
docker上部署程序后无法连接数据库的问题
咱就是说,这个问题差点给我劝退docker。下面说下环境情况。 装了个javaweb程序容器,装了个数据库容器,javaweb容器就是链接不上数据库。 咱也是跟着菜鸟教程的容器互联步骤简历网络链接: 并且启动时增加--networkxxx 都加入到了…...

Ucore lab4
实验目的 了解内核线程创建/执行的管理过程了解内核线程的切换和基本调度过程 实验内容 练习一:分配并初始化一个进程控制块 1.内核线程及管理 内核线程是一种特殊的进程,内核线程与用户进程的区别有两个:内核线程只运行在内核态&#x…...

AI失业潮来袭,某些部门裁员过半
历史的车轮滚滚向前,每次生产力的大幅跃进,都会造成一批失业潮。想当年,纺纱机的出现让无数手工作坊的织布师傅失业。如今,在AI技术的催化下,同样的事正在互联网行业的各个领域重演。 疯狂的裁员浪潮 “AI15秒做的&am…...

git 撤销add/commit,以及更换源命令
前言:主要是为了自己方便记录,省的每次都查找一下这些命令 1、当我们只是想撤回commit,保留add .的时候,可以用下方代码 git reset --soft HEAD^ 2、当我们想撤回commit以及add .的时候,可以用下方代码 git reset…...

3dMax需要什么样的硬件环境才能更好的工作?
3dMax官方给出了系统要求的列表 ,可用于帮助确保系统中的硬件能够与他们的软件一起工作。但是,这个“系统要求”列表只涵盖了运行软件所需硬件的最基本知识,而不是实际提供最佳性能的硬件。由于这些列表的不一致程度,我们花时间进行测试以确定运行 3dMax 的最佳硬件。基于…...
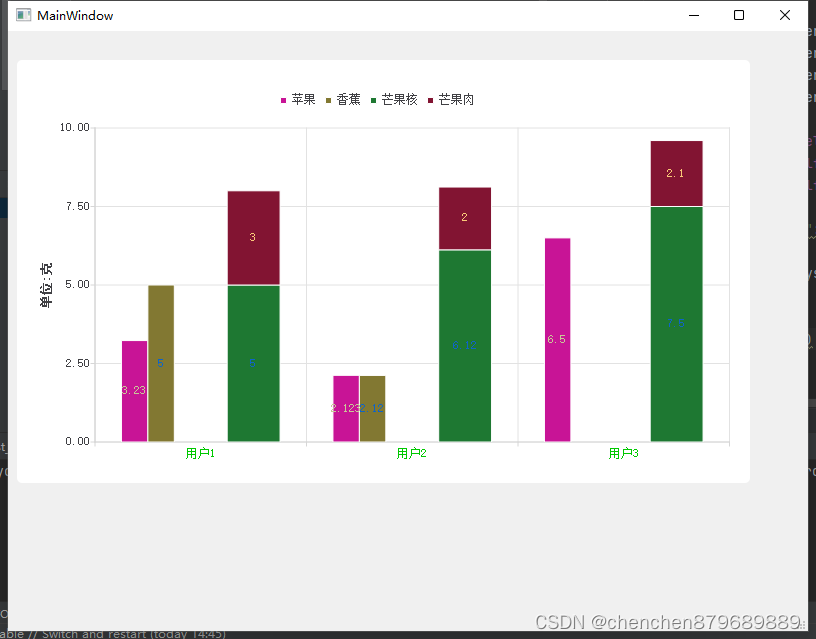
python-使用Qchart总结4-绘制多层柱状图
1、上代码 import sysfrom PyQt5.QtChart import QChart, QChartView, QBarCategoryAxis, QValueAxis, QBarSeries, QBarSet from PyQt5.QtGui import QPainter, QColor from PyQt5.QtWidgets import QMainWindow, QApplicationfrom untitled import Ui_MainWindow #从生成好的…...

Java学习笔记-02
目录 流程控制语句 分支语句 循环语句 Random随机数 数组 方法 流程控制语句 分为顺序语句(从上到下,依次执行),分支语句(if,else...)和循环语句(for,while,do...while) 分支语句 分为if与switch两大类 单分…...

中通快递财报预测:中通快递2023年收入和利润将大幅下降
来源:猛兽财经 作者:猛兽财经 市场对中通快递2023年的预测 卖方虽然预测中通快递(ZTO)在2023年的表现会很不错,但他们也预计中通快递今年的财务业绩将不会像去年那样好。 根据S&P Capital IQ的数据,卖…...

Javaweb | 状态管理:Session、Cookie
💗wei_shuo的个人主页 💫wei_shuo的学习社区 🌐Hello World ! 状态管理 问题引入 HTTP协议是无转态的,不能保存提交的信息如果用户发来一个新的请求,服务器无法知道它是否与上次的请求联系对于那些需要多次…...

大数据学习栈记——Neo4j的安装与使用
本文介绍图数据库Neofj的安装与使用,操作系统:Ubuntu24.04,Neofj版本:2025.04.0。 Apt安装 Neofj可以进行官网安装:Neo4j Deployment Center - Graph Database & Analytics 我这里安装是添加软件源的方法 最新版…...

STM32+rt-thread判断是否联网
一、根据NETDEV_FLAG_INTERNET_UP位判断 static bool is_conncected(void) {struct netdev *dev RT_NULL;dev netdev_get_first_by_flags(NETDEV_FLAG_INTERNET_UP);if (dev RT_NULL){printf("wait netdev internet up...");return false;}else{printf("loc…...

基于Flask实现的医疗保险欺诈识别监测模型
基于Flask实现的医疗保险欺诈识别监测模型 项目截图 项目简介 社会医疗保险是国家通过立法形式强制实施,由雇主和个人按一定比例缴纳保险费,建立社会医疗保险基金,支付雇员医疗费用的一种医疗保险制度, 它是促进社会文明和进步的…...

(二)TensorRT-LLM | 模型导出(v0.20.0rc3)
0. 概述 上一节 对安装和使用有个基本介绍。根据这个 issue 的描述,后续 TensorRT-LLM 团队可能更专注于更新和维护 pytorch backend。但 tensorrt backend 作为先前一直开发的工作,其中包含了大量可以学习的地方。本文主要看看它导出模型的部分&#x…...

YSYX学习记录(八)
C语言,练习0: 先创建一个文件夹,我用的是物理机: 安装build-essential 练习1: 我注释掉了 #include <stdio.h> 出现下面错误 在你的文本编辑器中打开ex1文件,随机修改或删除一部分,之后…...

渲染学进阶内容——模型
最近在写模组的时候发现渲染器里面离不开模型的定义,在渲染的第二篇文章中简单的讲解了一下关于模型部分的内容,其实不管是方块还是方块实体,都离不开模型的内容 🧱 一、CubeListBuilder 功能解析 CubeListBuilder 是 Minecraft Java 版模型系统的核心构建器,用于动态创…...

基础测试工具使用经验
背景 vtune,perf, nsight system等基础测试工具,都是用过的,但是没有记录,都逐渐忘了。所以写这篇博客总结记录一下,只要以后发现新的用法,就记得来编辑补充一下 perf 比较基础的用法: 先改这…...

SpringCloudGateway 自定义局部过滤器
场景: 将所有请求转化为同一路径请求(方便穿网配置)在请求头内标识原来路径,然后在将请求分发给不同服务 AllToOneGatewayFilterFactory import lombok.Getter; import lombok.Setter; import lombok.extern.slf4j.Slf4j; impor…...
的原因分类及对应排查方案)
JVM暂停(Stop-The-World,STW)的原因分类及对应排查方案
JVM暂停(Stop-The-World,STW)的完整原因分类及对应排查方案,结合JVM运行机制和常见故障场景整理而成: 一、GC相关暂停 1. 安全点(Safepoint)阻塞 现象:JVM暂停但无GC日志,日志显示No GCs detected。原因:JVM等待所有线程进入安全点(如…...

dify打造数据可视化图表
一、概述 在日常工作和学习中,我们经常需要和数据打交道。无论是分析报告、项目展示,还是简单的数据洞察,一个清晰直观的图表,往往能胜过千言万语。 一款能让数据可视化变得超级简单的 MCP Server,由蚂蚁集团 AntV 团队…...
