二叉搜索树【Java】
文章目录
- 二叉搜索树的性质
- 二叉搜索树的操作
- 遍历
- 查找
- 插入
- 删除
二叉搜索树又称为二叉排序树,是一种具有一定性质的特殊的二叉树;
二叉搜索树的性质
若它的左子树不为空,则左子树上结点的值均小于根节点的值;
若它的右子树不为空,则右子树上结点的值均大于根节点的值;
二叉搜索树的左右子树均为二叉搜索树;
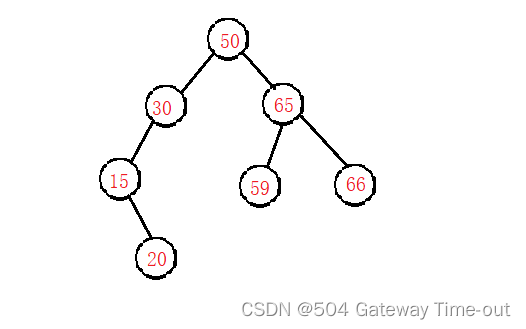
二叉搜索树的操作
遍历
关于二叉树的遍历方式有前序、中序、后序三种,对于二叉搜索树而言,使用中序遍历得到的结点序列是有序的;
public class BinarySearchTree {
//首先创建相关的结点结构static class TreeNode {public int key;public TreeNode left;public TreeNode right;TreeNode(int key){this.key=key;}}public TreeNode root;//进行中序遍历public void inorder(TreeNode root){if (root==null) return;inorder(root.left);System.out.println(root.key+" ");inorder(root.right);}
}
查找
基于二叉搜索树的性质,当根节点不为空时,可以根据根节点的值与待查找的值key之间的关系进行查找;即若根节点的值大于key,则在其左子树进行查找;若根节点的值小于key,则到其右子树进行查找;直到最终根节点的值为空或没有找到key则结束;
public TreeNode search(int key){//定义一个cur从根节点的位置开始查找TreeNode cur=root;while (cur!=null){//结点的值与key相等,找到并返回if (cur.key==key){return cur;}else if(cur.key<key){//结点的值小于key,去其右子树进行查找cur=cur.right;}else {//结点的值大于key,去其左子树进行查找cur=cur.left;}}//没有找到,没有该值return null;}
插入
插入操作可以分为2种情况:当根节点为空时,直接插入到根节点即可;当根节点不为空时,就需要遵守搜索树的性质按照之前查找的逻辑,将节点插入合适的位置,保证不破坏其二叉搜索树的结构;
public boolean insert (int key){//结点为空,直接进行插入if (root==null){root=new TreeNode(key);return true;}//结点不为空//定义一个cur寻找插入的合适位置TreeNode cur=root;//记录cur的位置或走向TreeNode parent=null;//寻找合适的插入位置,使用parent记录while (cur!=null){if (cur.key<key){parent=cur;cur=cur.right;}else if (cur.key<key){parent=cur;cur=cur.left;}else{//不可以插入相同的数据return false;}}//创建新结点TreeNode node=new TreeNode(key);if (parent.key<key){parent.right=node;}else{parent.left=node;}return true;}
删除
删除操作相较于前面的查找插入操作要略显复杂,大致可以分为下面几种情况:
设待删除的结点为cur,待删除节点的双亲结点为parent;
- cur.left==null;
cur是root;
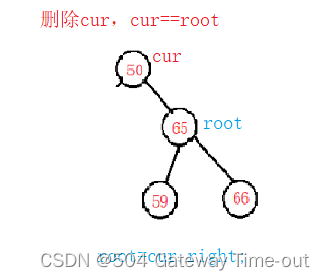
cur不是root,又可以分为2种情况:
cur是其双亲结点parent的左结点:
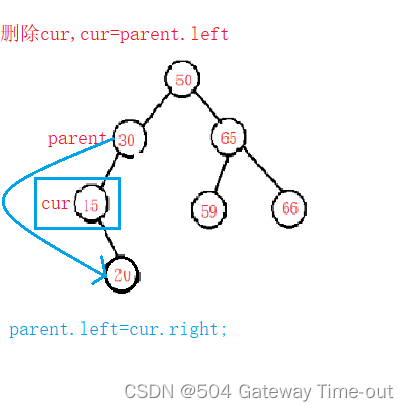
cur是其双亲结点parent的右结点:
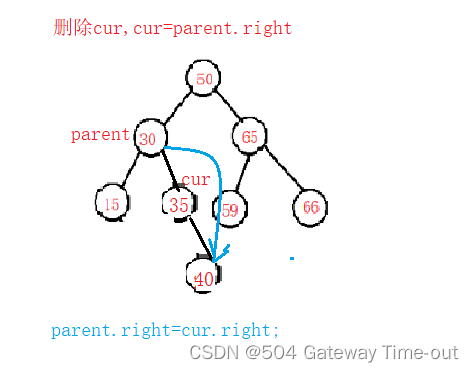
- cur.right==null;
cur为root;
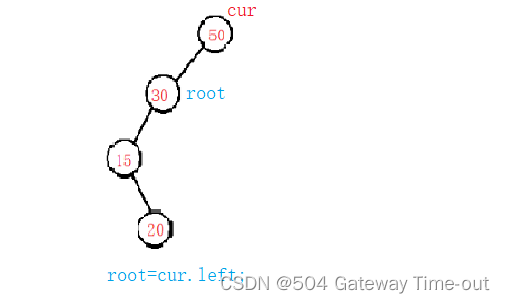
cur不是root,又可以分为2种情况:
cur是其双亲结点parent的左结点:
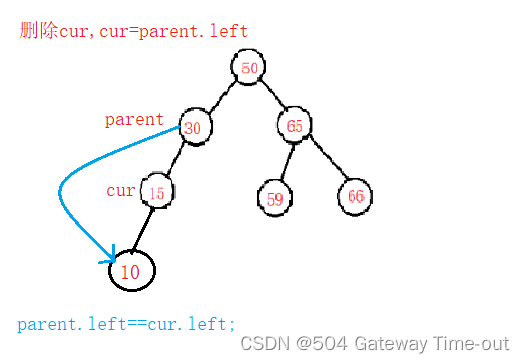
cur是其双亲结点parent的右结点:
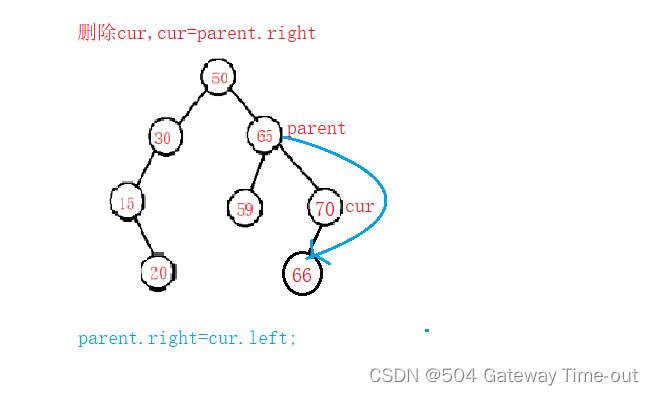
- cur.left!=null && cur.right!=null;
使用替换法进行删除,使用待删除节点的右子树的最小值将待删除节点进行替换,再删除最小值的结点即可;
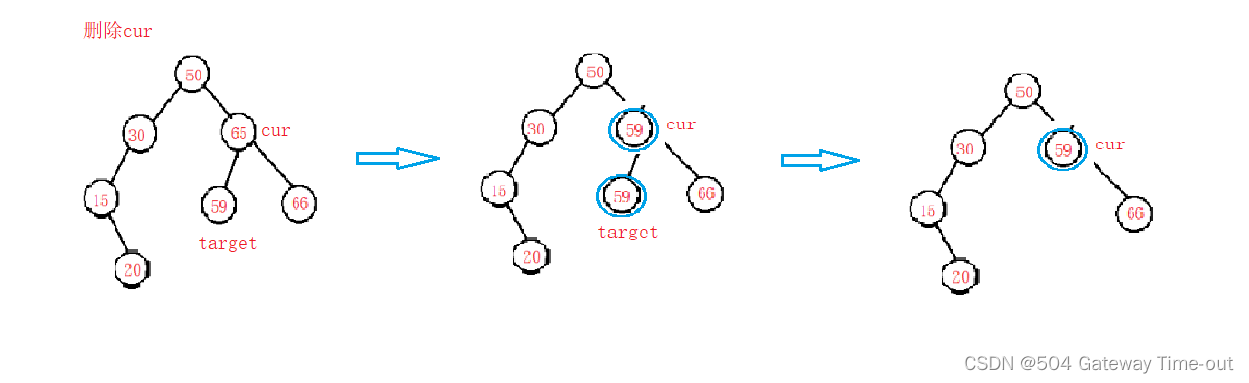
下面是具体的代码实现:
public boolean remove(int key){TreeNode cur=root;TreeNode parent=null;//寻找删除的结点的位置while (cur!=null){if (cur.key<key){parent=cur;cur=cur.right;}else if(cur.key==key){//调用removeNode方法进行具体的删除removeNode(parent,cur);return true;}else{parent=cur;cur=cur.left;}}return false;}private void removeNode(TreeNode parent, TreeNode cur) {//第一种情况if (cur.left==null){if (cur==root){root=cur.right;}else if(cur==parent.left){parent.left=cur.right;}else {parent.right=cur.right;}//第二种情况}else if(cur.right==null){if (cur==root){root=cur.left;}else if(cur==parent.left){parent.left=cur.left;}else {parent.right=cur.left;}}else{//第三种情况,使用替换法TreeNode targetParent=cur;TreeNode target=cur.right;//寻找最小值while (target.left!=null){targetParent=target;target=target.left;}//进行替换cur.key=target.key;//删除那个最小值if (target==targetParent.left){targetParent.left=target.right;}else{targetParent.right=target.right;}}}
对于这样一棵二叉搜索树而言,一般情况下结点所处的位置越深,需要进行比较的次数就越多。因此根据结点插入的次序不同,就可能得到不同结构的二叉树:
最好情况下,得到一棵完全二叉树的结构,平均比较次数达到logN(以2为底);
最坏情况下,得到一棵单分支树,平均比较次数为N/2;
over!
相关文章:

二叉搜索树【Java】
文章目录 二叉搜索树的性质二叉搜索树的操作遍历查找插入删除 二叉搜索树又称为二叉排序树,是一种具有一定性质的特殊的二叉树; 二叉搜索树的性质 若它的左子树不为空,则左子树上结点的值均小于根节点的值; 若它的右子树不为空&a…...

二叉树的遍历方式
文章目录 层序遍历——队列实现分析Java完整代码 先序遍历——中左右分析递归实现非递归实现——栈实现 中序遍历——左中右递归实现非递归实现——栈实现 后续遍历——左右中递归实现非递归实现——栈加标志指针实现 总结 层序遍历——队列实现 给你二叉树的根节点 root &…...
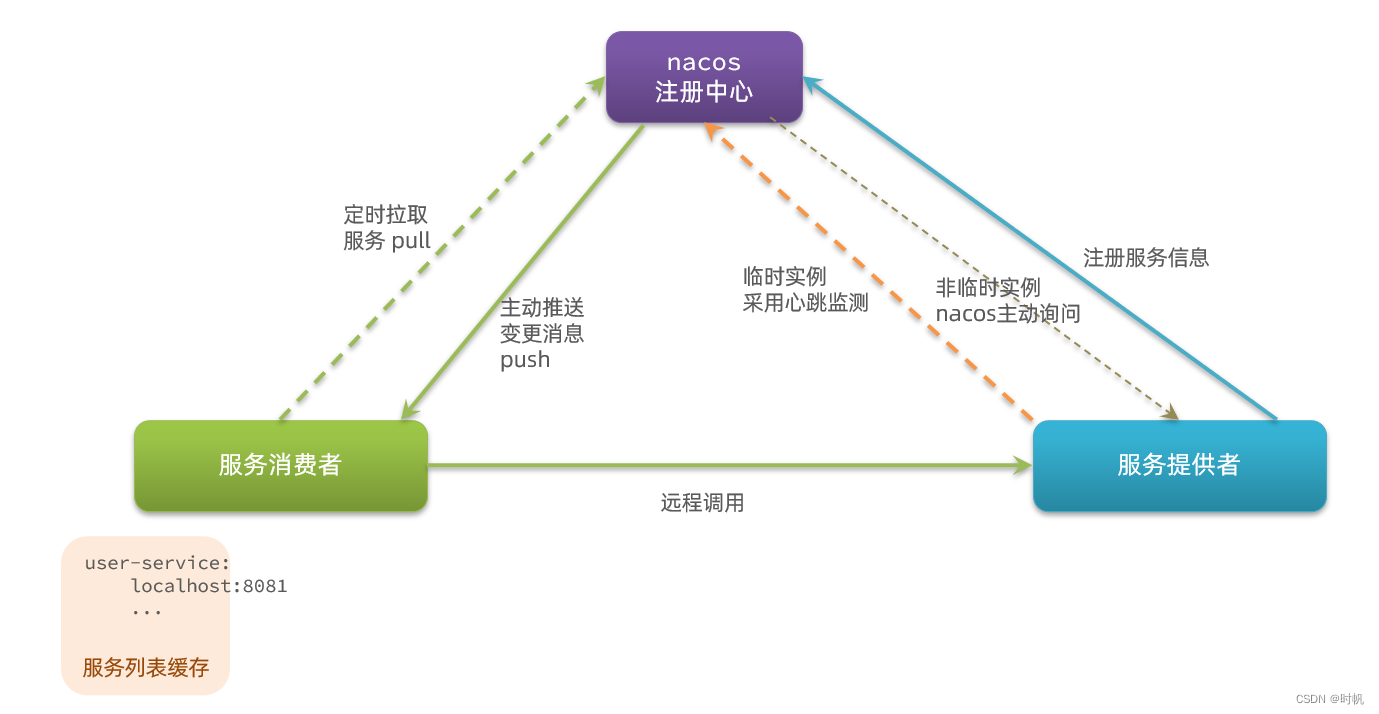
SpringCloud01
SpringCloud01 微服务入门案例 实现步骤 导入数据 实现远程调用 MapperScan("cn.itcast.order.mapper") SpringBootApplication public class OrderApplication {public static void main(String[] args) {SpringApplication.run(OrderApplication.class, args);}…...

SpringBoot整合Redis实现点赞、收藏功能
前言 点赞、收藏功能作为常见的社交功能,是众多Web应用中必不可少的功能之一。而redis作为一个基于内存的高性能key-value存储数据库,可以用来实现这些功能。 本文将介绍如何使用spring boot整合redis实现点赞、收藏功能,并提供前后端页面的…...

【Java入门合集】第一章Java概述
【Java入门合集】第一章Java概述 博主:命运之光 专栏:JAVA入门 学习目标 1.理解JVM、JRE、JDK的概念; 2.掌握Java开发环境的搭建,环境变量的配置; 3.掌握Java程序的编写、编译和运行; 4.学会编写第一个Java程序&#x…...

Android无线调试操作说明
1.首先通过手机机蓝牙将jackpal.androidterm-1.0.70.apk(终端模拟器)传的设备上安装 链接: https://pan.baidu.com/s/151SzEgsX0b_VTWowzfUrsA?pwdrn75 提取码: rn75 复制这段内容后打开百度网盘手机App,操作更方便哦 2.打开这个终端模拟器,输入以下命…...

什么是 Python ?聊一聊Python程序员找工作的六大技巧
最近我一直在思考换工作的事情。因此,这段时间我会看一些题目,看一些与面试相关的内容,以便更好地准备面试。我认为无论你处于什么阶段,面试中都会有技术面试环节。无论是初级职位还是高级职位,都需要通过技术面试来检…...

RabbitMQ 01 概述
什么是消息队列 进行大量的远程调用时,传统的Http方式容易造成阻塞,所以引入了消息队列的概念,即让消息排队,按照队列进行消费。 它能够将发送方发送的信息放入队列中,当新的消息入队时,会通知接收方进行处…...

面经|曹操出行供需策略运营
1.自我介绍 面试官表示看了简历之后,表示对专业能力比较放心。想了解下对于专业能力之外,关于其他方面的介绍。 2.策略运营,除了工具之外,还有哪些能力是需要具备的 回答:主要是从做项目的维度逻辑先去回答的。 分析思…...
【Python】selenium工具
目录 1. 安装 2. 测试 3. 无头浏览器 4. 元素定位 5. 页面滑动 6. 按键、填写登录表单 7. 页面切换 Selenium是Web的自动化测试工具,为网站自动化测试而开发,Selenium可以直接运行在浏览器上,它支持所有主流的浏览器,可以接…...
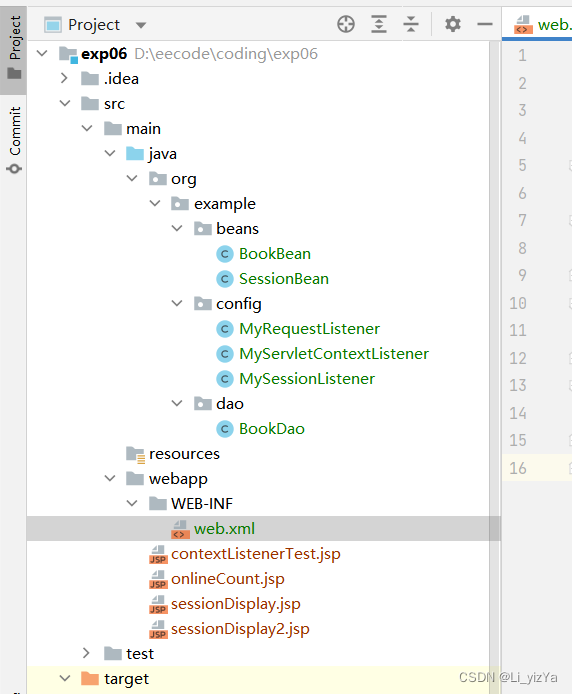
实验六~Web事件处理与过滤器
1. 创建一个名为exp06的Web项目,编写、部署、测试一个ServletContext事件监听器。 BookBean代码 package org.example.beans;import java.io.Serializable;/*** Created with IntelliJ IDEA.* Description:* User: Li_yizYa* Date: 2023—04—29* Time: 18:39*/ Su…...
刷题4.28
1、 开闭原则软件实体(模块,类,方法等)应该对扩展开放,对修改关闭,即在设计一个软件系统模块(类,方法)的时候,应该可以在不修改原有的模块(修改关…...

做了一年csgo搬砖项目,还清所有债务:会赚钱的人都在做这件事 !
前段時间,在网上看到一句话:有什么事情,比窮更可怕? 有人回答说:“又忙又窮。” 很扎心,却是绝大多数人的真实写照。 每天拼死拼活的996,你有算过你的時间值多少钱? 我们来算一笔…...
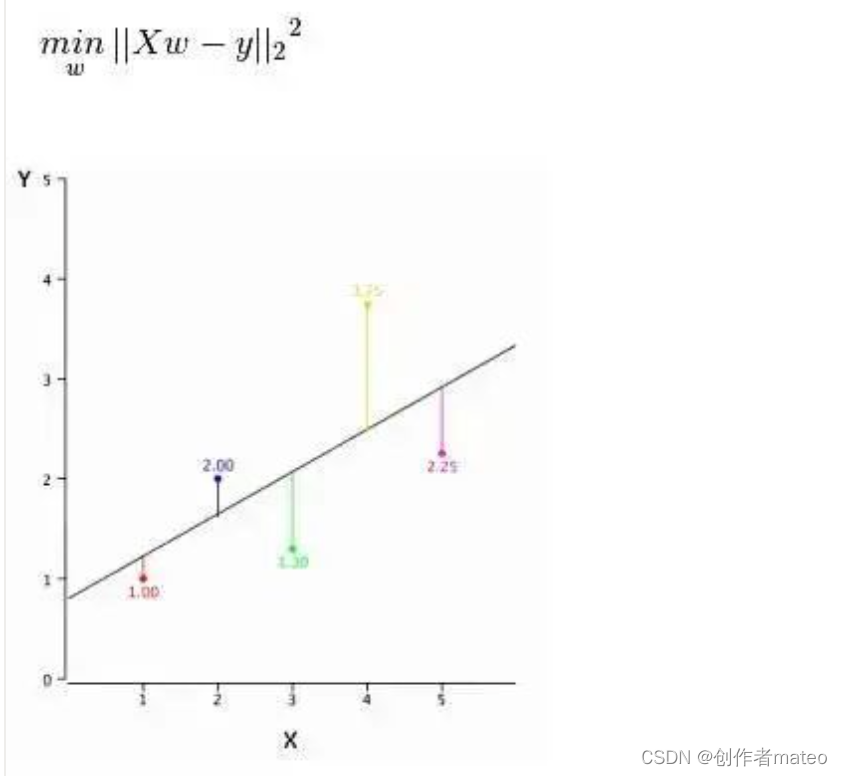
线性回归模型(7大模型)
线性回归模型(7大模型) 线性回归是人工智能领域中最常用的统计学方法之一。在许多不同的应用领域中,线性回归都是非常有用的,例如金融、医疗、社交网络、推荐系统等等。 在机器学习中,线性回归是最基本的模型之一&am…...
 A~D)
VP记录:Codeforces Round 868 (Div. 2) A~D
传送门:CF A题:A-characteristic 构造一个只有 1 , − 1 1,-1 1,−1的数组,满足乘积为 1 1 1的数对的个数为 k k k. 发现 n n n的范围很小,考虑直接暴力枚举数组中 1 1 1的个数,记为 i i i,那么对于1的所有数对来说,我们有 i ∗ ( i − 1 ) / 2 i*(i-1)/2 i∗(i−1)/2个,然后…...

【VQ-VAE-2论文精读】Generating Diverse High-Fidelity Images with VQ-VAE-2
【VQ-VAE-2论文精读】Generating Diverse High-Fidelity Images with VQ-VAE-2 0、前言Abstract1 Introduction2 Background2.1 Vector Quantized Variational AutoEncoder3 Method3.1 Stage 1: Learning Hierarchical Latent Codes3.2 Stage 2: Learning Priors over Latent C…...
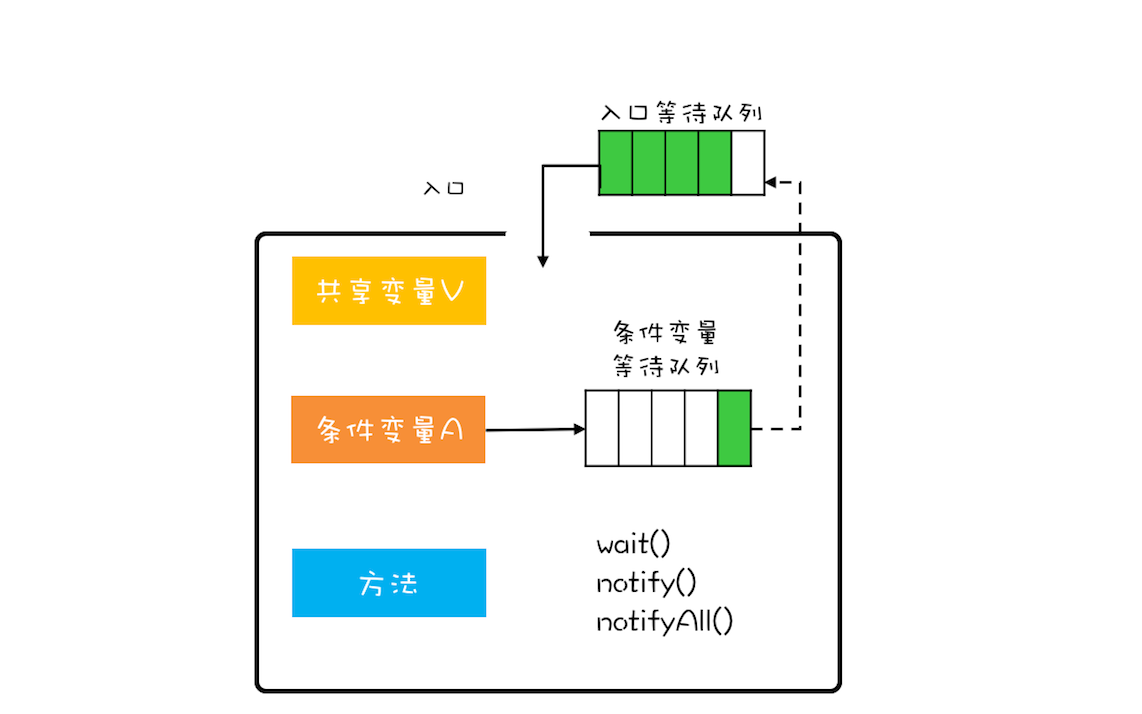
并发编程基石:管程
大家好,我是易安! 如果有人问我学习并发并发编程,最核心的技术点是什么,我一定会告诉他,管程技术。Java语言在1.5之前,提供的唯一的并发原语就是管程,而且1.5之后提供的SDK并发包,也…...
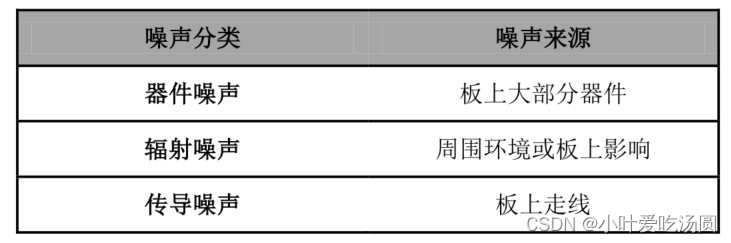
电路中噪声来源
电路包括不同的部件和芯片,所有都有可能成为噪声的来源。例如,电阻会带来热噪声,这个噪声为宽频噪声,几乎涵盖所有频率范围;运算放大器其芯片内部会产生噪声;而 ADC产生的量化噪声相较于其他器件࿰…...

JAVASE的全面总结
(未完待续) 五、子类与继承 5.1 子类与父类 继承是一种由已有的类创建新类的机制。利用继承,我们可以先创建一个共有属性的一般类,根据该一般类再创建具有特殊属性的新类,新类继承一般类的状态和行为,并…...
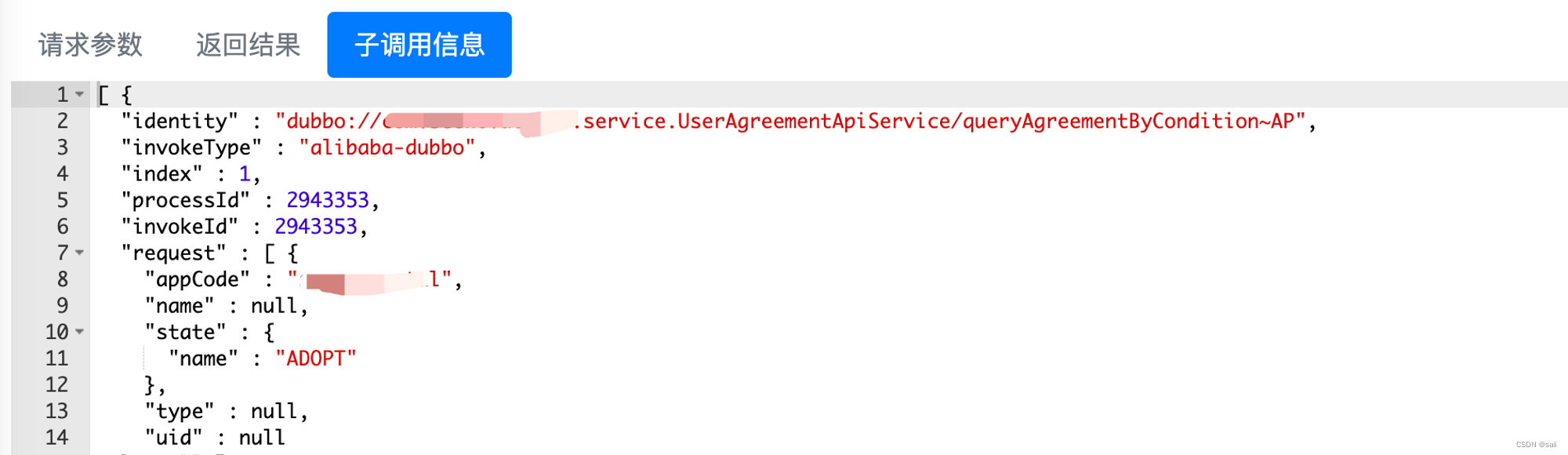
关于repeater录制的流量子调用的identity中带有~S的情况
前段时间同事问我,我们录制的流量中,尤其是dubbo的子调用显示经常他的末尾会带上一个小尾巴这个是什么意思呢,其实之前我没有太在意这个事情,只是同事这么疑问了,确实激起了好奇心,所以就差了下 到底是什么…...
详解)
后进先出(LIFO)详解
LIFO 是 Last In, First Out 的缩写,中文译为后进先出。这是一种数据结构的工作原则,类似于一摞盘子或一叠书本: 最后放进去的元素最先出来 -想象往筒状容器里放盘子: (1)你放进的最后一个盘子(…...

React hook之useRef
React useRef 详解 useRef 是 React 提供的一个 Hook,用于在函数组件中创建可变的引用对象。它在 React 开发中有多种重要用途,下面我将全面详细地介绍它的特性和用法。 基本概念 1. 创建 ref const refContainer useRef(initialValue);initialValu…...

【入坑系列】TiDB 强制索引在不同库下不生效问题
文章目录 背景SQL 优化情况线上SQL运行情况分析怀疑1:执行计划绑定问题?尝试:SHOW WARNINGS 查看警告探索 TiDB 的 USE_INDEX 写法Hint 不生效问题排查解决参考背景 项目中使用 TiDB 数据库,并对 SQL 进行优化了,添加了强制索引。 UAT 环境已经生效,但 PROD 环境强制索…...

Linux简单的操作
ls ls 查看当前目录 ll 查看详细内容 ls -a 查看所有的内容 ls --help 查看方法文档 pwd pwd 查看当前路径 cd cd 转路径 cd .. 转上一级路径 cd 名 转换路径 …...

React Native在HarmonyOS 5.0阅读类应用开发中的实践
一、技术选型背景 随着HarmonyOS 5.0对Web兼容层的增强,React Native作为跨平台框架可通过重新编译ArkTS组件实现85%以上的代码复用率。阅读类应用具有UI复杂度低、数据流清晰的特点。 二、核心实现方案 1. 环境配置 (1)使用React Native…...

电脑插入多块移动硬盘后经常出现卡顿和蓝屏
当电脑在插入多块移动硬盘后频繁出现卡顿和蓝屏问题时,可能涉及硬件资源冲突、驱动兼容性、供电不足或系统设置等多方面原因。以下是逐步排查和解决方案: 1. 检查电源供电问题 问题原因:多块移动硬盘同时运行可能导致USB接口供电不足&#x…...

【CSS position 属性】static、relative、fixed、absolute 、sticky详细介绍,多层嵌套定位示例
文章目录 ★ position 的五种类型及基本用法 ★ 一、position 属性概述 二、position 的五种类型详解(初学者版) 1. static(默认值) 2. relative(相对定位) 3. absolute(绝对定位) 4. fixed(固定定位) 5. sticky(粘性定位) 三、定位元素的层级关系(z-i…...
)
WEB3全栈开发——面试专业技能点P2智能合约开发(Solidity)
一、Solidity合约开发 下面是 Solidity 合约开发 的概念、代码示例及讲解,适合用作学习或写简历项目背景说明。 🧠 一、概念简介:Solidity 合约开发 Solidity 是一种专门为 以太坊(Ethereum)平台编写智能合约的高级编…...
相比,优缺点是什么?适用于哪些场景?)
Redis的发布订阅模式与专业的 MQ(如 Kafka, RabbitMQ)相比,优缺点是什么?适用于哪些场景?
Redis 的发布订阅(Pub/Sub)模式与专业的 MQ(Message Queue)如 Kafka、RabbitMQ 进行比较,核心的权衡点在于:简单与速度 vs. 可靠与功能。 下面我们详细展开对比。 Redis Pub/Sub 的核心特点 它是一个发后…...

C++:多态机制详解
目录 一. 多态的概念 1.静态多态(编译时多态) 二.动态多态的定义及实现 1.多态的构成条件 2.虚函数 3.虚函数的重写/覆盖 4.虚函数重写的一些其他问题 1).协变 2).析构函数的重写 5.override 和 final关键字 1&#…...
