软考算法-排序篇-上
数据排序
- 一:故事背景
- 二:直接插入排序
- 2.1 概念
- 2.2 画图表示
- 2.3 代码实现
- 2.4 总结提升
- 三:希尔排序
- 3.1 概念
- 3.2 画图表示
- 3.3 代码实现
- 3.4 总结提升
- 四:直接选择排序
- 4.1 概念
- 4.2 画图表示
- 4.3 代码实现
- 4.4 总结提升
- 五:堆排序
- 5.1 概念
- 5.1.1 堆
- 5.1.2 堆排序
- 5.2 画图表示
- 5.3 代码实现
- 5.4 总结提升
- 六:表格比较
- 七:总结&提升
一:故事背景
最近在准备5月底的软件工程师的考试,这个考试最困难的就是算法部分了。接下来的文章我将会总结 排序与算法,希望通过此系列文章的总结,能让我们不但把握住考试的试题,更可以学会分析算法,写出优秀的算法,优化我们的代码。
二:直接插入排序
2.1 概念
- 在插入第 i 个记录时,R1,R2,…Ri-1 都已经排好序。这时候将第 i 个记录依次与 Ri-1 … R2,R1 进行比较,找到合适的位置插入,插入位置及之后的记录依次向后移动
2.2 画图表示
只看概念描述可能不是很好理解,让我们来画图理解一下,这个算法。
- 首先给出一组待排序的数字

- 根据上述概念,我们必须从第二个开始进行排序,因为第一个数据之前没有数据,对第一个数据比价是没有意义的。
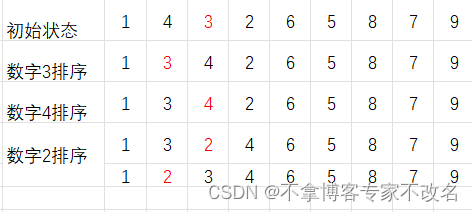
通过观察规律和结合概念描述,我们可以看出。整个顺序是前面的部分,逐渐有序的。那个数据需要排序,那么它之前的数据一定是有序的。例如:数字4排序前,它前面的数字为 1,3,是有序的, 数字2排序前,它前面的数字为 1,3,4是有序的,根据以上规律依次类推就可以将数据进行从小到大排序
2.3 代码实现
上文给出了对应算法的图,相信通过此图,大家对直接插入算法有了一定的了解,那让我们来看看,如何用代码去实现直接插入算法吧
- 算法代码
public static void insertionSort(int[] nums) {//首先记录数组的长度int len = nums.length;//从数组的第二个元素开始for (int i = 1; i < len; i++) {//依次取出一个元素,存储在current变量中Integer current = nums[i];//定义一个指针,初始化当前元素的前一个位置int j = i - 1;//重复上述操作,直到找到一个位置j,使得 nums[j] <= current,或者 j 已经到达数组的起始位置。while (j >= 0 && nums[j] > current) {nums[j + 1] = nums[j];j--;}nums[j + 1] = current;}}
- 执行代码
public class Main {public static void main(String[] args) {int[] nums = {1,4, 3, 2,6,5,8,7,9};System.out.println("排序前"+Arrays.toString(nums));Sort1.insertionSort(nums);System.out.println("排序后"+Arrays.toString(nums));}
}
- 运行结果

上述代码中核心点有两个:
- 一个是循环的边界。
外层for循环的边界是从第二个元素开始,到最后一个循环结束。
内层的while循环的边界是到第一个数据并且找到的数据必须比当前操作的数据大。 - 一个是数据的交换。
数据交换主要体现在内层的while循环中,如果符合条件则将比当前 j指针标记的数向后移动一个。最后找到符合条件的位置时,将当前操作的数 current 放到指定位置。
2.4 总结提升
上述给出了直接插入排序的算法分析与实例。直接插入排序算法在最好情况下(数据完全有序)时间复杂度为O(n),最坏的情况下(数据无序)为O(n²)。此算法属于比较简单的算法。希望大家通过我的博客能够理解此算法。
三:希尔排序
3.1 概念
- 希尔排序又称“缩小增量排序”,他是对“直接插入排序的改进”。
- 希尔排序的思想是:先将整个待排记录分割成若干个子序列,然后分别进行直接插入排序,待整个序列中的记录基本有序时,再对全体进行一次直接插入排序。
3.2 画图表示
希尔排序的核心点是:** 分隔子序列 **,将待排数组分割成子序列,分别进行排序。具体的分隔数没有特别要求,一般初始值是待排数列的一半,然后依次减半,直至最后间隔为1为止。

上图中,给出了一个待排数组的变化。
- 待排数组长度为8,所以子序列间隔分别为 4 2 1
- 间隔为4时,一共有4组数据,将这四组数据进行直接插入排序,保证这四组数据有序。
- 间隔为2时,一共有2组数据,将这两组数据进行直接插入排序,保证这两组数据有序。
- 间隔为1时,整体进行直接插入排序,但是这时数据已经基本有序,需要移动的数据很少。
3.3 代码实现
下文给出** 希尔排序** 的具体实现:
public static void shellSort(int[] arr) {//交换的次数int num = 0;int n = arr.length;// 初始化增量gap为数组长度的一半for (int gap = n / 2; gap > 0; gap /= 2) {System.out.println("gap值" + gap);// 对于每个增量gap,进行一次插入排序for (int i = gap; i < n; i++) {//temp表示当前操作的元素int temp = arr[i];//j是一个指针,表示当前操作的元素int j = i;// 对于每个元素,向前比较gap个距离的元素。如果前面的元素大于当前元素才需要交换while (j >= gap && arr[j - gap] > temp) {//后面元素挪到前面arr[j] = arr[j - gap];//当前操作元素变为前gap个j -= gap;}//将本次需要操作元素放到移动的位置arr[j] = temp;num++;System.out.println(gap + Arrays.toString(arr));}}System.out.println("一共交换了:"+ num +"次");}
3.4 总结提升
希尔排序是一种不稳定的排序算法。其时间复杂度约为O(n¹·³),在排序过程中需要一个元素的辅助空间用于元素值交换,空间爱你复杂的为O(1)。
相对于直接插入排序而言,希尔排序的时间复杂度更低,效率更高,对于大规模数据排序更加适用。
四:直接选择排序
4.1 概念
直接选择排序是一种简单排序算法,它的基本思想是:在待排的数据中选取最小值,与当前值进行交换,直至交换完毕。
4.2 画图表示
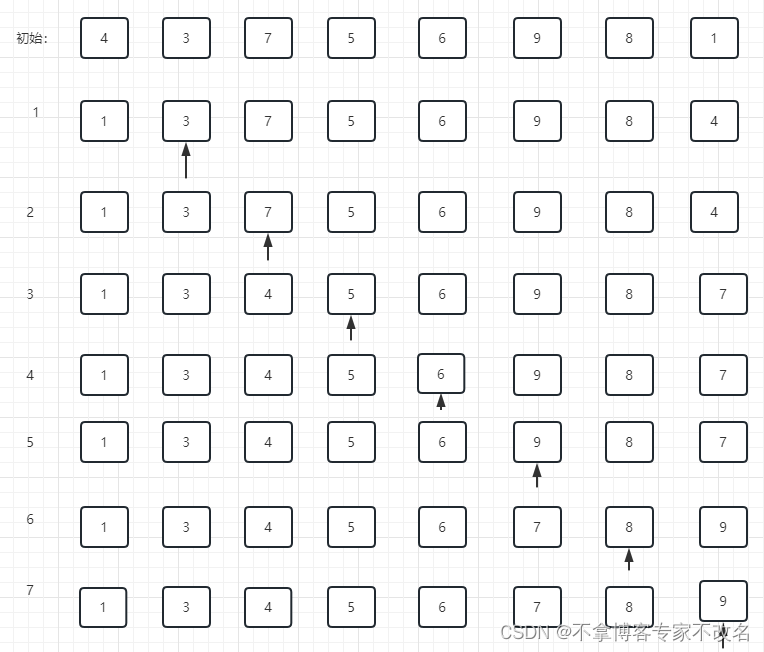
4.3 代码实现
/*** @BelongsProject: algorithm* @BelongsPackage: org.example* @Author:hlzs1* @Description: 直接选择排序* @CreateTime: 2023-04-28 10:44* @Version: 1.0*/
public class Sort3 {public static void SelectionSort(int[] arr) {int length = arr.length;for (int i = 0; i < length-1 ; i++) {//从当然开始筛选int minIndex = i;for (int j = i+1; j < length; j++) {if(arr[minIndex] >arr[j]){minIndex = j;}}//交换数值int current = arr[i];arr[i] = arr[minIndex];arr[minIndex] = current;}}}4.4 总结提升
- 直接选择排序的时间复杂度为 O(n^2),其中 n 是待排序数组的长度。具体来说,它的时间复杂度由两个嵌套循环决定。
- 直接选择排序的时间复杂度为 O(n^2),其中 n 是待排序数组的长度。具体来说,它的时间复杂度由两个嵌套循环决定。
五:堆排序
5.1 概念
- 在计算机科学中,堆(Heap)是一种特殊的树形数据结构,它通常是一个近似完全二叉树,其中父节点的值总是大于或小于它的子节点。具体而言,堆被分为两种类型:最大堆(Max Heap)和最小堆(Min Heap)。
- 在最大堆中,每个节点的值都大于或等于其子节点的值。因此,最大堆的根节点是堆中的最大元素。在最小堆中,每个节点的值都小于或等于其子节点的值。因此,最小堆的根节点是堆中的最小元素。
5.1.1 堆
5.1.2 堆排序
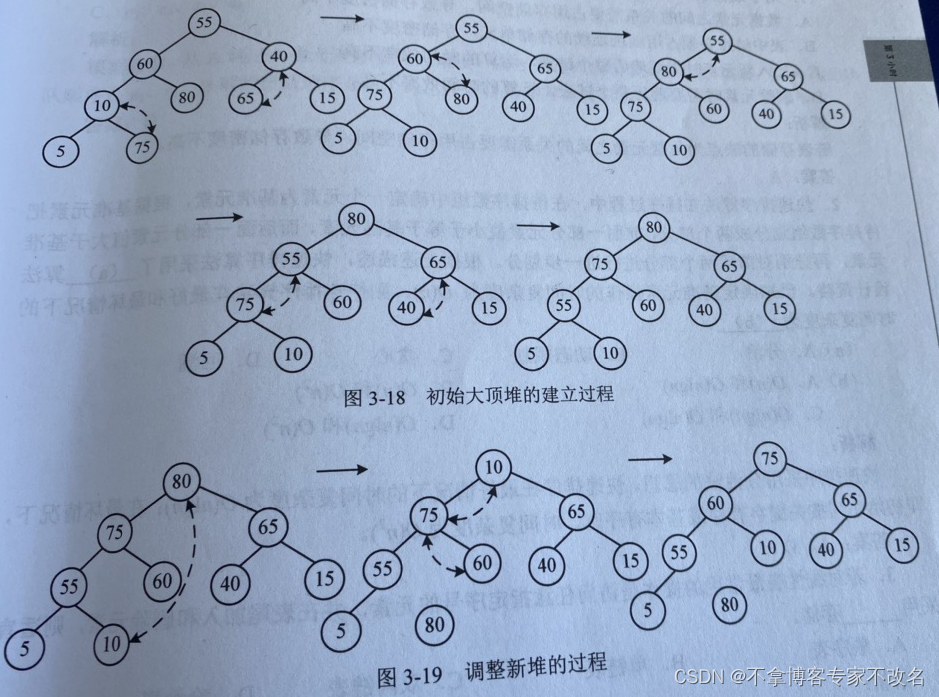
- 对一组待排序元素,首先按照堆的定义排成一个序列(建立初始堆),之后输出堆顶最大元素(对于大顶堆而言)
- 然后将剩余的元素在调整成新堆,从而得到次大元素,如此反复,直到全部元素有序为止。
5.2 画图表示
5.3 代码实现
public static void heapSort(int[] arr) {//判断如果arr为空或者只有一个数据,则不需要进行排序if (arr == null || arr.length < 2) {return;}//构建大根堆for (int i = 0; i < arr.length; i++) {heapInsert(arr, i);}//将堆顶元素依次放到数组最后,并重新调整堆结构int size = arr.length;swap(arr, 0, --size);while (size > 0) {heapify(arr, 0, size);swap(arr, 0, --size);}}//构建大根堆public static void heapInsert(int[] arr, int index) {//如果while (arr[index] > arr[(index - 1) / 2]) {swap(arr, index, (index - 1) / 2);index = (index - 1) / 2;}}//调整大根堆public static void heapify(int[] arr, int index, int size) {int left = index * 2 + 1;while (left < size) {int largest = left + 1 < size && arr[left + 1] > arr[left] ? left + 1 : left;largest = arr[largest] > arr[index] ? largest : index;if (largest == index) {break;}swap(arr, largest, index);index = largest;left = index * 2 + 1;}}//交换数组中的两个元素public static void swap(int[] arr, int i, int j) {int temp = arr[i];arr[i] = arr[j];arr[j] = temp;}//测试public static void main(String[] args) {int[] arr = {4, 6, 2, 9, 1, 8, 5, 3, 7};heapSort(arr);System.out.println(Arrays.toString(arr));}
5.4 总结提升
堆排序是一种不稳定的排序,与直接插入排序很像,每次都是筛选出一个最值,但是不同的是,堆排序利用了树的结构,进行了排序。
六:表格比较
| 算法名 \ 比较项 | 时间复杂度 | 空间复杂度 | 稳定性 |
|---|---|---|---|
| 直接插入排序 | O(n) ~ O(n²) | O(1) | 稳定 |
| 希尔排序 | 约为O(n¹·³) | O(1) | 不稳定 |
| 直接选择排序 | O(n²) | O(1) | 稳定 |
| 堆排序 | O(nlogn) | O(1) | 不稳定 |
七:总结&提升
本文给出了直接插入排序、希尔排序、直接选择排序、堆排序的。概念、图、和代码。希望大家通过此篇文章能理解什么是算法,各个算法的不同作用,这对我们以后看源码,自己编写代码有很大的好处,可以很好的训练我们的思维。
本篇为上篇,接下来的文章,我会继续输出关于数据排序的另外四种算法,有兴趣的朋友请持续关注我~
相关文章:

软考算法-排序篇-上
数据排序 一:故事背景二:直接插入排序2.1 概念2.2 画图表示2.3 代码实现2.4 总结提升 三:希尔排序3.1 概念3.2 画图表示3.3 代码实现3.4 总结提升 四:直接选择排序4.1 概念4.2 画图表示4.3 代码实现4.4 总结提升 五:堆…...

总结836
学习目标: 4月(复习完高数18讲内容,背诵21篇短文,熟词僻义300词基础词) 学习内容: 暴力英语:背诵《keep your direction》,默写,英语语法 高等数学:刷题&a…...

ginbuilder 工具快速创建
ginbuilder github 地址 快速创建一个ginweb项目: 目前apps下只有http服务,如果后续有需要的话,会添加上rpc服务,websocket服务后边如果有需要会添加上swagger 创建完成的目录结构 ├── apps │ ├── apis // 所有的apis…...

【Java基础面试宝典】堆、栈、方法区分别都存储了那些内容?wait 和 sleep 方法的区别?
目录 堆、栈、方法区分别都存储了那些内容? 堆(heap) 栈(stack) 方法区(method) 在 java 中 wait 和 sleep 方法的区别? 堆、栈、方法区分别都存储了那些内容? 堆&a…...

古剑飞仙手游Linux系统服务器架设教程
安装宝塔直接运行命令即可。 yum install -y wget && wget -O install.sh http://download.bt.cn/install/install_6.0.sh && sh install.sh 搭建环境: centos 7以上系统服务器 宝塔面板安装应用如下: Nginx1.14 mysql5.7 php5.6 1…...
(附python示例代码))
python实战应用讲解-【numpy数组篇】常用函数(十)(附python示例代码)
目录 Python Numpy MaskedArray.ravel()函数 Python Numpy MaskedArray.reshape()函数 Python Numpy MaskedArray.resize()函数 Python Numpy MaskedArray.std()函数 Python Numpy MaskedArray.sum()函数 Python Numpy MaskedArray.swapaxes()函数 Python Numpy MaskedA…...
练习题#2)
计算机组成原理(考研408)练习题#2
用于复习408或计算机组成原理期末考试。如有错误请在评论区指出。 So lets start studying with questions! それでは、問題の勉強を始めましょう! 11.某 cache 采用全相联映射,假设 cache 有 3 块,程序运行过程中需要访问的主存块号依 次为…...
Apache POI,springboot中导出excel报表
2. Apache POI 2.1 介绍 Apache POI 是一个处理Miscrosoft Office各种文件格式的开源项目。简单来说就是,我们可以使用 POI 在 Java 程序中对Miscrosoft Office各种文件进行读写操作。 一般情况下,POI 都是用于操作 Excel 文件。 Apache POI 的应用场景…...
-- 三种样式表)
CSS(一)-- 三种样式表
目录 1. 行内样式表 2. 内部样式表 3. 外部样式表(即引入 .css文件)(重点掌握) 1. 行内样式表 行内样式表(内联样式表)是在元素标签内部的 style 属性中设定 CSS 样式。适合于修改简单样式。 <di…...

嵌入式之Samba服务器搭建
在嵌入式系统开发应用平台中,tftp、nfs和samba服务器是最常用的文件传输工具 tftp和nfs是在嵌入式Linux开发环境中经常使用的传输工具 samba则是Linux和Windows之间的文件传输工具。 下面演示在linux上搭建Samba服务器 sudo apt-get install samba chmod -R 77…...
vue3+go——看到了就去学习吧
vue3go——看到了就去学习吧 Vue3.2 Vite Element-Plus 实现最基础的 CRUD1.效果展示【02:36】2.创建项目【03:16】3.添加github管理【04:10】4.引入element-plus【04:21】5.内容布局【08:59】6.布局优化【05:31】7.添加弹窗【09:34】8.ref改$ref【02:47】9.新增数据【09:22】…...

Perf工具统计CPU性能
Perf 性能检测工具 Perf 是一个内置于Linux内核中的工具,用于性能分析和调优。它可以对系统的CPU使用情况、内存使用情况、磁盘I/O、网络I/O等进行监控和分析,并提供了丰富的分析和可视化工具,以帮助用户定位和解决性能问题。perf可以进行函…...
考验大家指针功底的时候到了:请问如何理解 (int*)1 + 1 ?
来,猜猜看,这里的执行结果是什么? 这是今天课上的一道理解题,给大家一点点思考时间。 (心里有答案了再往下滑哦) 5 4 3 2 1 . 答案是,报warning!因为%d不是用来输出指针的哈…...

英语基础-介词
介词 方位介词 in:在…里面 Its in the box. 在盒子里 in my backpack 在背包里 in the tree 长在树上on:在…上面(指与物体表面接触) Its on the box. 在盒子上(和盒子接触) on the floor.在地板上 on the tree.在树上under:在…下面 Its unde…...
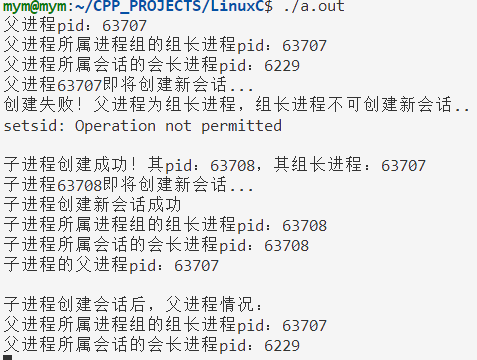
Linux进程通信:进程组 会话
1. 进程组 (1)概念:一个或多个进程的集合,也称为“作业”。 (2)父进程创建子进程时,默认属于同一个进程组。进程组ID为组长进程ID。 (3)进程组中只要有一个进程存在&a…...

【前端面经】JS-深浅拷贝
理解深浅拷贝 深浅拷贝问题的出现是由于JavaScript对不同类型的存储方式而引发的。 对于原始数据类型,它们的值是直接存储在栈内存中; 而复杂数据类型,则在栈内存中记录它的指针,而指针指向堆内存中真正的值。 所以对于原始数据类…...

【自然语言处理】实验2布置:Word2Vec TransE案例
NLP_class 学堂在线《自然语言处理》实验课代码报告,授课老师为刘知远老师。课程链接:https://www.xuetangx.com/training/NLP080910033761/1017121?channeli.area.manual_search。 持续更新中。 所有代码为作者所写,并非最后的“标准答案…...
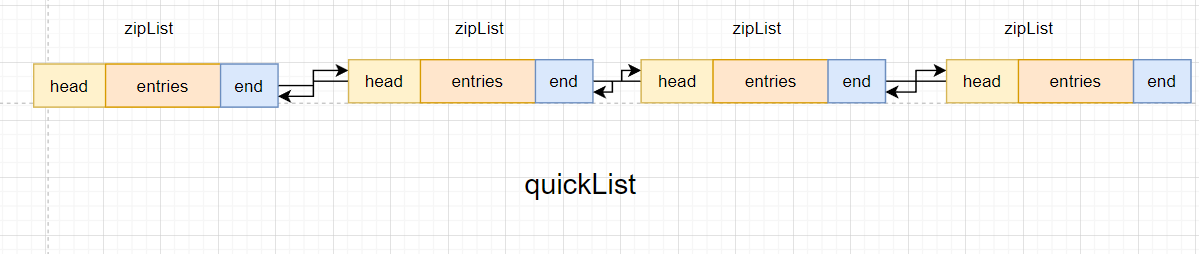
Redis集合底层实现原理
目录 本章重点简单动态字符串SDS集合底层实现原理zipListlistPackskipListquickListKey 与Value中元素的数量 本章重点 掌握Redis简单动态字符串了解Redis集合底层实现原理 简单动态字符串SDS SDS简介 我们Redis中无论是key还是value其数据类型都是字符串.我们Redis中的字符…...

OVS常用命令与使用总结
OVS常用命令与使用总结 说明 在平时使用ovs中,经常用到的ovs命令,参数,与举例总结,持续更新中… 进程启动 1.先准备ovs的工作目录,数据库存储路径等 mkdir -p /etc/openvswitch mkdir -p /var/run/openvswitch …...
一以贯之:从城市网络到“城市一张网”
《论语里仁》中子曰:“参乎,吾道一以贯之”。 孔子所说的“一以贯之”,逐渐成为了中国文化与哲学的重要组成部分,指明事物发展往往需要以标准化、集约化、融合化作为目标。这种智慧在数字化发展中格外重要。从云计算、大数据技术模…...

ES6从入门到精通:前言
ES6简介 ES6(ECMAScript 2015)是JavaScript语言的重大更新,引入了许多新特性,包括语法糖、新数据类型、模块化支持等,显著提升了开发效率和代码可维护性。 核心知识点概览 变量声明 let 和 const 取代 var…...

【JVM】- 内存结构
引言 JVM:Java Virtual Machine 定义:Java虚拟机,Java二进制字节码的运行环境好处: 一次编写,到处运行自动内存管理,垃圾回收的功能数组下标越界检查(会抛异常,不会覆盖到其他代码…...

pam_env.so模块配置解析
在PAM(Pluggable Authentication Modules)配置中, /etc/pam.d/su 文件相关配置含义如下: 配置解析 auth required pam_env.so1. 字段分解 字段值说明模块类型auth认证类模块,负责验证用户身份&am…...

【第二十一章 SDIO接口(SDIO)】
第二十一章 SDIO接口 目录 第二十一章 SDIO接口(SDIO) 1 SDIO 主要功能 2 SDIO 总线拓扑 3 SDIO 功能描述 3.1 SDIO 适配器 3.2 SDIOAHB 接口 4 卡功能描述 4.1 卡识别模式 4.2 卡复位 4.3 操作电压范围确认 4.4 卡识别过程 4.5 写数据块 4.6 读数据块 4.7 数据流…...

华为OD机试-食堂供餐-二分法
import java.util.Arrays; import java.util.Scanner;public class DemoTest3 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseint a in.nextIn…...

[10-3]软件I2C读写MPU6050 江协科技学习笔记(16个知识点)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16...

全面解析各类VPN技术:GRE、IPsec、L2TP、SSL与MPLS VPN对比
目录 引言 VPN技术概述 GRE VPN 3.1 GRE封装结构 3.2 GRE的应用场景 GRE over IPsec 4.1 GRE over IPsec封装结构 4.2 为什么使用GRE over IPsec? IPsec VPN 5.1 IPsec传输模式(Transport Mode) 5.2 IPsec隧道模式(Tunne…...
)
.Net Framework 4/C# 关键字(非常用,持续更新...)
一、is 关键字 is 关键字用于检查对象是否于给定类型兼容,如果兼容将返回 true,如果不兼容则返回 false,在进行类型转换前,可以先使用 is 关键字判断对象是否与指定类型兼容,如果兼容才进行转换,这样的转换是安全的。 例如有:首先创建一个字符串对象,然后将字符串对象隐…...

使用 SymPy 进行向量和矩阵的高级操作
在科学计算和工程领域,向量和矩阵操作是解决问题的核心技能之一。Python 的 SymPy 库提供了强大的符号计算功能,能够高效地处理向量和矩阵的各种操作。本文将深入探讨如何使用 SymPy 进行向量和矩阵的创建、合并以及维度拓展等操作,并通过具体…...

Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决
Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决 问题背景 在一个基于 Spring Cloud Gateway WebFlux 构建的微服务项目中,新增了一个本地验证码接口 /code,使用函数式路由(RouterFunction)和 Hutool 的 Circle…...
