【C++】布隆过滤器
文章目录
- 布隆过滤器提出
- 布隆过滤器概念
- 布隆过滤器应用场景
- 设计思路:
- 布隆过滤器的插入
- 布隆过滤器的查找
- 布隆过滤器删除
- BloomFilter.h
- 布隆过滤器优点
- 布隆过滤器缺陷
布隆过滤器提出
我们在使用新闻客户端看新闻时,它会给我们不停地推荐新的内容,它每次推荐时要去重,去掉那些已经看过的内容
问题来了,新闻客户端推荐系统如何实现推送去重的?
答:用服务器记录了用户看过的所有历史记录,当推荐系统推荐新闻时会从每个用户的历史记录里进行筛选,过滤掉那些已经存在的记录
那问题又来了,如何快速查找呢?
- 用哈希表存储用户记录,缺点:浪费空间
- 用位图存储用户记录,缺点:不能处理哈希冲突
- 将哈希与位图结合,即布隆过滤器
布隆过滤器概念
位图:节省空间,效率高 ,但是有局限性:只能处理整数 但是布隆过滤器可以处理字符串,自定义类型
布隆过滤器是由布隆(Burton Howard Bloom)在1970年提出的 一种紧凑型的、比较巧妙的概率型数据结构,特点是高效地插入和查询,可以用来告诉你 “某样东西一定不存在或者可能存在”,它是用多个哈希函数,将一个数据映射到位图结构中,此种方式不仅可以提升查询效率,也可以节省大量的内存空间
例子:
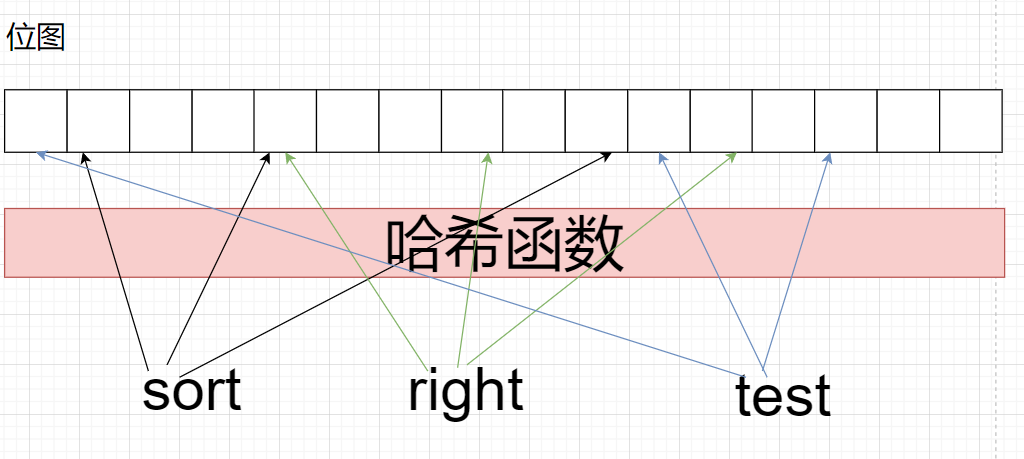
布隆过滤器中一个值通过多个哈希函数,在位图中有多个映射位置,即使一个位置发生冲突了,还有另外的映射的值,降低了冲突的概率,由于映射多个位置,因此可能不同的值,处于同一个位置,虽然不能保证这个值一定存在,但是可以保证一个值一定不存在,因为只要有一个映射的位置为0,就说明该值不存在
问题:布隆过滤器会误判存在还是会误判不存在?
- 存在可能会误判! 因为会产生哈希冲突,不同的字符串可能会映射在同一个位置, 一个字符串不存在但是可能会被误判成存在
- 为了减少减少误判,通常采用多个哈希函数来映射多个位置 即一个值映射多个位置
是一定会有哈希冲突的!!!因为整数是有限的,字符串是无限的
布隆过滤器应用场景
布隆过滤器会存在误判,所以通常应用在允许误判的场景之中
一般应用场景:数据量大,节省空间,允许误判
-
黑名单校验
发现存在黑名单中的,就执行特定操作,比如:识别垃圾邮件,只要是邮箱在黑名单中的邮件,就识别为垃圾邮件,假设黑名单的数量是数以亿计的,存放起来就是非常耗费存储空间的,布隆过滤器则是一个较好的解决方案,把所有黑名单都放在布隆过滤器中,再收到邮件时,判断邮件地址是否在布隆过滤器中即可, -
身份验证:
大门口的身份验证,如果不是小区里面的人,直接就拒绝进入(不在是确定的),如果通过了布隆过滤器的判断,再去数据库中对比一次,这样通过一层布隆过滤器可以提高这个查找系统的效率 -
检测手机号是否注册过
系统所有用户的电话号码都存储再数据库的用户表 . 如果这个手机号不在布隆过滤器就肯定没有注册过, 如果在布隆过滤器,那么这里可能存在误判,再查一次数据库复核一下
设计思路:
首先我们需要确定位图开辟多大的空间
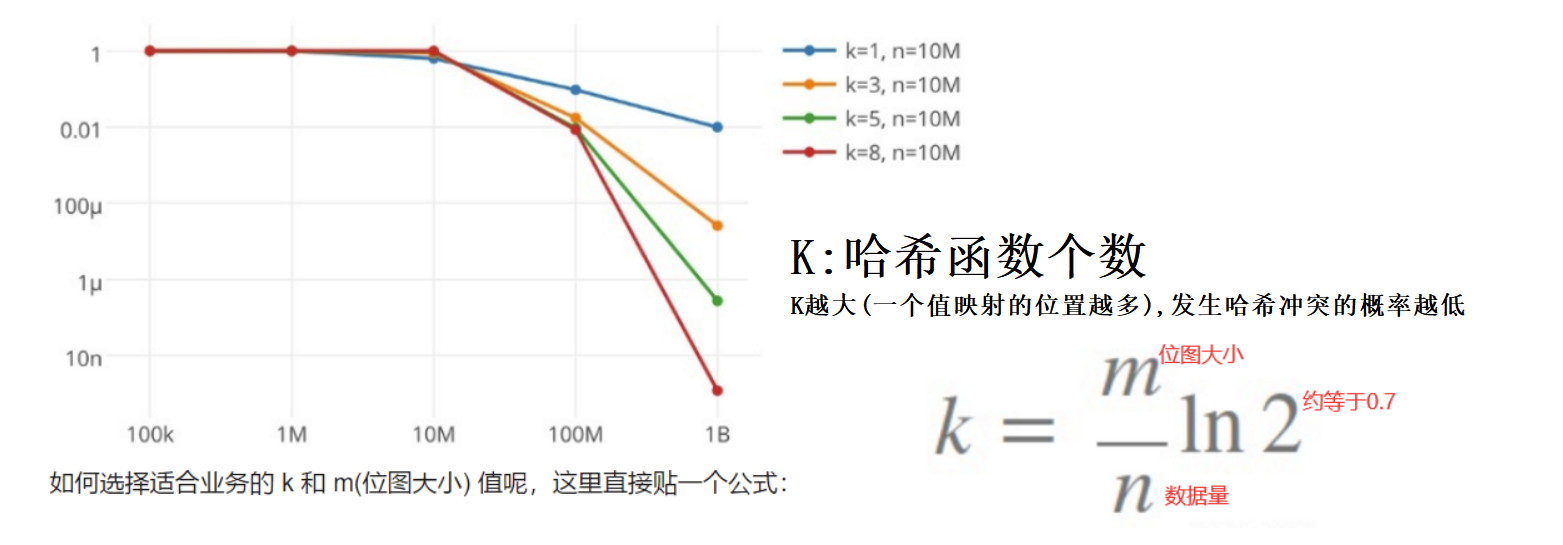
假设k为3, 则->位图的大小大致应该为: m = 4.2*n
先准备几个哈希函数用于将字符串转为整形
//BKDR算法
struct BKDRHash
{size_t operator()(const string& s){// BKDRsize_t value = 0;for (auto ch : s){value *= 31;value += ch;}return value;}
};struct APHash
{size_t operator()(const string& s){size_t hash = 0;for (long i = 0; i < s.size(); i++){if ((i & 1) == 0){hash ^= ((hash << 7) ^ s[i] ^ (hash >> 3));}else{hash ^= (~((hash << 11) ^ s[i] ^ (hash >> 5)));}}return hash;}
};struct DJBHash
{size_t operator()(const string& s){size_t hash = 5381;for (auto ch : s){hash += (hash << 5) + ch;}return hash;}
};
template<size_t N> 非类型模板参数,共插入多少个值
size_t X = 4, //X值越大,产生冲突的概率越低, N*X表示位图开辟多少个比特位空间,利用公式计算X
class K = string,
class HashFunc1 = BKDRHash,//一个字符串想映射几个比特位就给几个HashFunc仿函数计算哈希地址
class HashFunc2 = APHash,
class HashFunc3 = DJBHash>class BloomFilter
{
public:
private:bitset<X*N> _bs;
};
布隆过滤器的插入
将值对应的每个哈希函数计算出的位置都置为1
//将key所映射的位置设为1
void Set(const K& key)
{size_t len = N * X;//总长度 //计算映射的哈希地址 HashFunc()是匿名对象size_t index1 = HashFunc1()(key) % len;size_t index2 = HashFunc2()(key) % len;size_t index3 = HashFunc3()(key) % len;//将对应的映射位置标志为1_bs.set(index1);_bs.set(index2);_bs.set(index3);
}
布隆过滤器的查找
布隆过滤器的思想是将一个元素用多个哈希函数映射到一个位图中 因此被映射到的位置的比特位一定为1,所以可以按照以下方式进行查找:
- 分别计算每个哈希值对应的比特位置存储的是否为0, 只要有一个映射位置为0代表该元素一定不在哈希表中
- 否则可能在哈希表中(因为存在误判)
//判断key是否在布隆过滤器中
bool Test(const K& key)
{//三个映射为都是1才在(可能存在误判),其中一个不是1就不在size_t len = N * X;size_t index1 = HashFunc1()(key) % len;size_t index2 = HashFunc2()(key) % len;size_t index3 = HashFunc3()(key) % len;if ( (!_bs.test(index1)) || (!_bs.test(index2)) || (!_bs.test(index3))){return false;}return true;//可能存在误判
}
注意:布隆过滤器如果说某个元素不存在时,该元素一定不存在, 如果**该元素存在时,该元素可能存在也可能不存在.**因为有些哈希函数存在一定的误判
布隆过滤器删除
布隆过滤器不能直接支持删除工作, 因为在删除一个元素时可能会影响其他元素,因为不确定当前位置,是自己的,还是发生了哈希冲突其它的值映射过来的
如何支持修改呢? ->存储引用计数(有几个值映射在当前位置)
将布隆过滤器中的每个比特位扩展成一个小的计数器,插入元素时给k个计数器(k个哈希函数计算出的哈希地址)加一, 删除元素时给k个计数器减一,通过多占用几倍存储空间的代价来增加删除操作
但是这种方法不太好, 因为计数器的大小不易确定,如果给小了,发生冲突会导致溢出(计数回绕:即最大值溢出变为 最小值) 如果给大了浪费空间,脱离了布隆过滤器的本质思想,
缺陷:
- 无法确认元素是否真正在布隆过滤器中
- 存在计数回绕
BloomFilter.h
#define _CRT_SECURE_NO_WARNINGS 1
#pragma once//BKDR算法
struct BKDRHash
{size_t operator()(const string& s){// BKDRsize_t value = 0;for (auto ch : s){value *= 31;value += ch;}return value;}
};struct APHash
{size_t operator()(const string& s){size_t hash = 0;for (long i = 0; i < s.size(); i++){if ((i & 1) == 0){hash ^= ((hash << 7) ^ s[i] ^ (hash >> 3));}else{hash ^= (~((hash << 11) ^ s[i] ^ (hash >> 5)));}}return hash;}
};struct DJBHash
{size_t operator()(const string& s){size_t hash = 5381;for (auto ch : s){hash += (hash << 5) + ch;}return hash;}
};template<size_t N, 非类型模板参数,共插入多少个值
size_t X = 4, //X值越大,产生冲突的概率越低, N*X表示位图开辟多少个比特位空间
class K = string,// 假设布隆过滤器中元素类型为K,默认为string类型
//每个元素对应3个哈希函数
class HashFunc1 = BKDRHash,//一个字符串想映射几个比特位就给几个HashFunc仿函数计算哈希地址
class HashFunc2 = APHash,
class HashFunc3 = DJBHash>
class BloomFilter
{
public://将key所在的三个映射位设为1void Set(const K& key){size_t len = N * X;//总长度 //计算映射的哈希地址 HashFunc()是匿名对象size_t index1 = HashFunc1()(key) % len;size_t index2 = HashFunc2()(key) % len;size_t index3 = HashFunc3()(key) % len;//将对应的映射位置标志为1_bs.set(index1);_bs.set(index2);_bs.set(index3);}//判断key是否在布隆过滤器中bool Test(const K& key){//三个映射为都是1才在(可能存在误判),其中一个不是1就不在size_t len = N * X;size_t index1 = HashFunc1()(key) % len;size_t index2 = HashFunc2()(key) % len;size_t index3 = HashFunc3()(key) % len;if ( (!_bs.test(index1)) || (!_bs.test(index2)) || (!_bs.test(index3))){return false;}return true;//可能存在误判 }
// 不支持删除,删除可能会影响其他值,
// 一般情况不支持删除,why?->多个值可能会标记一个位,删除可能会影响其他key
// 如果非要支持删除的话,标记不再使用一个比特位,可以使用多个比特位,进行计数多少个值映射的这个比特位
// 但是这种方法是杀敌一千,自损八百的做法,因为消耗的更多的空间void Reset(const K& key);
private://此时k为3 则此时位图的大小大致应该为: m = 4.2*n 即X = 4bitset<N*X> _bs;
};
void TestBloomFilter()
{BloomFilter<100> bf;//最多存100个值 -》开辟100*4个比特位srand(time(0));size_t N = 100;std::vector<std::string> v2;for (size_t i = 0; i < N; ++i){std::string url = "https://www.cnblogs.com/-clq/archive/2012/05/31/2528153.html";url += std::to_string(6789 + i);v2.push_back(url);}size_t n2 = 0;for (auto& str : v2){if (bf.Test(str)){++n2;}}cout << "相似字符串误判率:" << (double)n2 / (double)N << endl;
}
布隆过滤器优点
-
增加和查询元素的时间复杂度为:O(K), (K为哈希函数的个数,一般比较小),与数据量大小无关
-
哈希函数相互之间没有关系,方便硬件并行运算
-
布隆过滤器不需要存储元素本身,在某些对保密要求比较严格的场合有很大优势
-
在能够承受一定的误判时,布隆过滤器比其他数据结构有这很大的空间优势
-
数据量很大时,布隆过滤器可以表示全集,其他数据结构不能
-
使用同一组散列函数的布隆过滤器可以进行交、并、差运算
布隆过滤器缺陷
- 有误判率,即存在假阳性(False Position),即不能准确判断元素是否在集合中(补救方法:再建立一个白名单,存储可能会误判的数据)
- 不能获取元素本身
- 一般情况下不能从布隆过滤器中删除元素
- 如果采用计数方式删除,可能会存在计数回绕问题
相关文章:

【C++】布隆过滤器
文章目录 布隆过滤器提出布隆过滤器概念布隆过滤器应用场景设计思路:布隆过滤器的插入布隆过滤器的查找布隆过滤器删除BloomFilter.h布隆过滤器优点布隆过滤器缺陷 布隆过滤器提出 我们在使用新闻客户端看新闻时,它会给我们不停地推荐新的内容,它每次推荐时要去重,去掉那些已经…...

功能齐全的 ESP32 智能手表,具有多个表盘、心率传感器硬件设计
相关设计资料下载ESP32 智能手表带心率、指南针设计资料(包含Arduino源码+原理图+Gerber+3D文件).zip 介绍 我们调查了智能手表项目的不同方面,并学会了集成和测试每个单独的部分。在本文中,我们将使用所学知识,结合使用硬件和软件组件,从头开始创建我们自己的智能手表。在…...
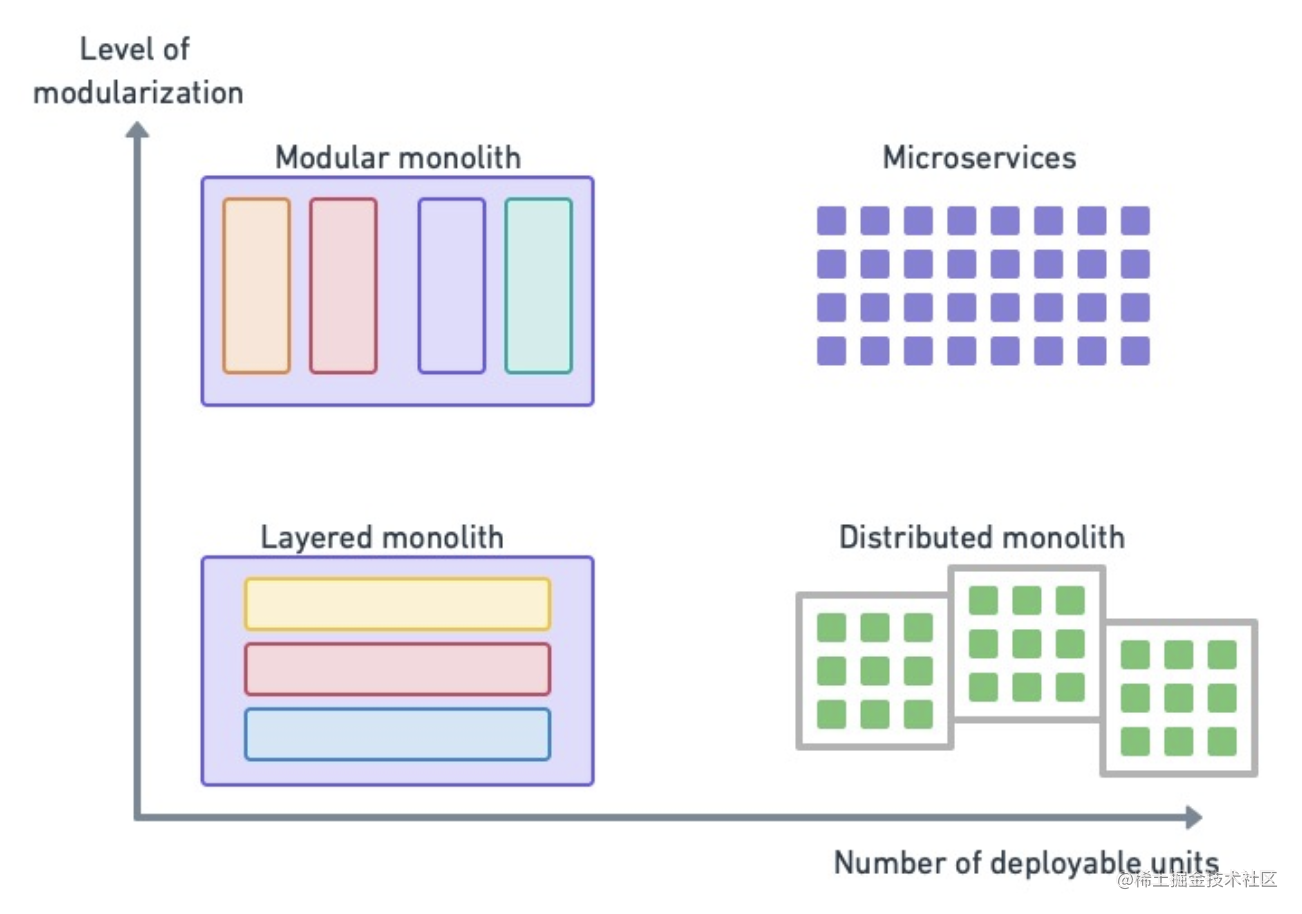
微服务不是本地部署的最佳选择,不妨试试模块化单体
微服务仅适用于成熟产品 关于从头开始使用微服务,马丁・福勒(Martin Fowler)总结道: 1. 几乎所有成功的微服务都是从一个过于庞大而不得不拆分的单体应用开始的。 2. 几乎所有从头开始以微服务构建的系统,最后都会因…...
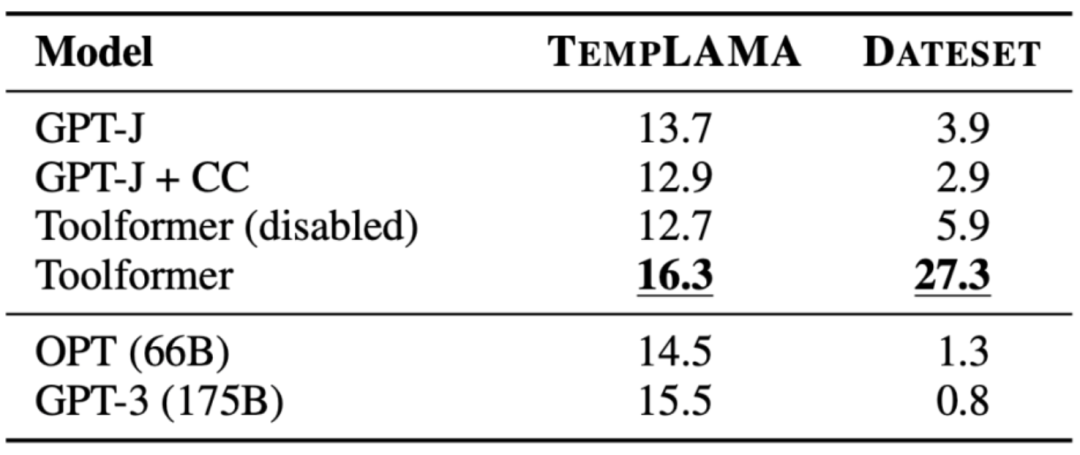
解读Toolformer
【引子】读论文Toolformer: Language Models Can Teach Themselves to Use Tools,https://arxiv.org/pdf/2302.04761.pdf,再阅读了几篇关于Toolformer的网络热文,于是“无知者无畏”,开始自不量力地试图解读Toolformer。 大语言模…...

FCOS3D Fully Convolutional One-Stage Monocular 3D Object Detection 论文学习
论文地址:Fully Convolutional One-Stage Monocular 3D Object Detection Github地址:Fully Convolutional One-Stage Monocular 3D Object Detection 1. 解决了什么问题? 单目 3D 目标检测由于成本很低,对于自动驾驶任务非常重…...

Xpath学习笔记
Xpath原理:先将HTML文档转为XML文档,再用xpath查找HTML节点或元素 什么是xml? 1、xml指可扩展标记语言 2、xml是一种标记原因,类似于html 3、xml的设计宗旨是传输数据,而非显示数据 4、xml标签需要我们自己自定义 5、x…...
网络编程之 Socket 套接字(使用数据报套接字和流套接字分别实现一个小程序(附源码))
文章目录 1. 什么是网络编程2. 网络编程中的基本概念1)发送端和接收端2)请求和响应3)客户端和服务端4)常见的客户端服务端模型 3. Socket 套接字1)Socket 的分类2)Java 数据报套接字通信模型3)J…...

What Are Docker Image Layers?
Docker images consist of multiple layers that collectively provide the content you see in your containers. But what actually is a layer, and how does it differ from a complete image? In this article you’ll learn how to distinguish these two concepts and…...

范数详解-torch.linalg.norm计算实例
文章目录 二范数F范数核范数无穷范数L1范数L2范数 前些天发现了一个巨牛的人工智能学习网站,通俗易懂,风趣幽默,忍不住分享一下给大家。点击跳转到网站。 范数是一种数学概念,可以将向量或矩阵映射到非负实数上,通常被…...

postgresdb备份脚本
以下是一个简单的postgresdb备份脚本示例: 复制 #!/bin/bash # 设置备份目录和文件名 BACKUP_DIR/path/to/backup BACKUP_FILEdb_backup_$(date %F_%H-%M-%S).sql # 设置数据库连接参数 DB_HOSTlocalhost DB_PORT5432 DB_NAMEmydatabase DB_USERmyusername DB_PA…...

MATLAB程序员投简历的技巧解析,如何写出有亮点的简历
如果你想在简历中展示你的项目经验,一定要有亮点。一个导出的 Excel 文件过大导致浏览器卡顿的例子就是一个很好的亮点。你可以在简历中写明这个例子。如果面试官问起,可以用浏览器的原理来解释。浏览器内核可以简单地分为以下 5 个线程:GUI …...

颜色空间转换RGB-YCbCr
颜色空间 颜色空间(Color Space)是描述颜色的一种方式,它是一个由数学模型表示的三维空间,通常用于将数字表示的颜色转换成可见的颜色。颜色空间的不同取决于所选的坐标轴和原点,以及用于表示颜色的色彩模型。在计算机…...

年薪40万程序员辞职炒股,把一年工资亏光了,得了抑郁症,太惨了
年薪40万的程序员辞职全职炒股 把一年的工资亏光了 得了抑郁症 刚才在网上看了一篇文章 是一位北京的一位在互联网 大厂上班的程序员 在去年就是股市行情比较好的时候 他买了30多万股票 结果连续三个月都赚钱 然后呢 他是就把每天就996这种工作就辞掉了 然后在家全是炒股 感觉炒…...
10分钟如何轻松掌握JMeter使用方法?
目录 引言 安装jmeter HTTP信息头管理器 JMeter断言 HTTP请求默认值来代替所有的域名与端口 JSON提取器来替换变量 结语 引言 想要了解网站或应用程序的性能极限,JMeter是一个不可或缺的工具。但是,对于初学者来说,该如何上手使用JMe…...
[NLP]如何训练自己的大型语言模型
简介 大型语言模型,如OpenAI的GPT-4或Google的PaLM,已经席卷了人工智能领域。然而,大多数公司目前没有能力训练这些模型,并且完全依赖于只有少数几家大型科技公司提供技术支持。 在Replit,我们投入了大量资源来建立从…...
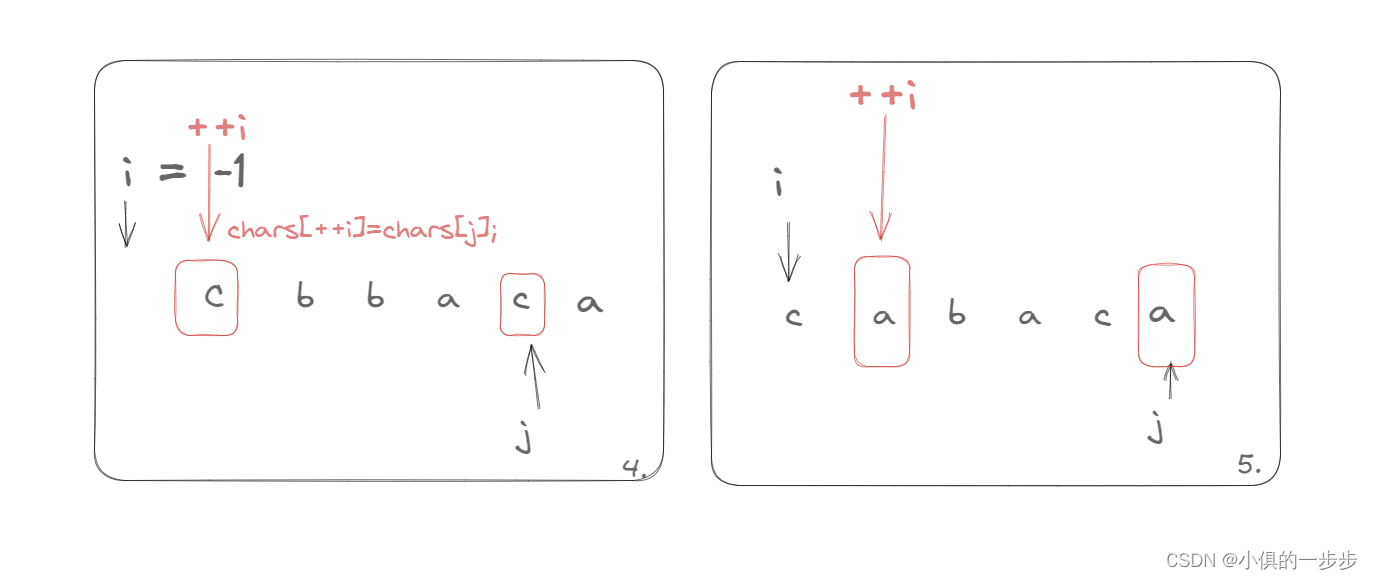
LeetCode1047. 删除字符串中的所有相邻重复项
1047. 删除字符串中的所有相邻重复项 给出由小写字母组成的字符串 S,重复项删除操作会选择两个相邻且相同的字母,并删除它们。 在 S 上反复执行重复项删除操作,直到无法继续删除。 在完成所有重复项删除操作后返回最终的字符串。答案保证唯一…...
)
3。数据结构(3)
嵌入式软件开发第三部分,各类常用的数据结构及扩展,良好的数据结构选择是保证程序稳定运行的关键,(1)部分包括数组,链表,栈,队列。(2)部分包括树,…...

QT停靠窗口QDockWidget类
QT停靠窗口QDockWidget类 QDockWidget类简介函数和方法讲解 QDockWidget类简介 QDockWidget 类提供了一个部件,它可以停靠在 QMainWindow 内或作为桌面上的顶级窗口浮动。 QDockWidget 提供了停靠窗口部件的概念,也称为工具面板或实用程序窗口。 停靠窗…...

【LeetCode】139. 单词拆分
139. 单词拆分(中等) 思路 首先将大问题分解成小问题: 前 i 个字符的子串,能否分解成单词;剩余子串,是否为单个单词; 动态规划的四个步骤: 确定 dp 数组以及下标的含义 dp[i] 表示 s…...

【三维重建】NeRF原理+代码讲解
文章目录 一、技术原理1.概览2.基于神经辐射场(Neural Radiance Field)的体素渲染算法3.体素渲染算法4.位置信息编码(Positional encoding)5.多层级体素采样 二、代码讲解1.数据读入2.创建nerf1.计算焦距focal与其他设置2.get_emb…...

基于大模型的 UI 自动化系统
基于大模型的 UI 自动化系统 下面是一个完整的 Python 系统,利用大模型实现智能 UI 自动化,结合计算机视觉和自然语言处理技术,实现"看屏操作"的能力。 系统架构设计 #mermaid-svg-2gn2GRvh5WCP2ktF {font-family:"trebuchet ms",verdana,arial,sans-…...

51c自动驾驶~合集58
我自己的原文哦~ https://blog.51cto.com/whaosoft/13967107 #CCA-Attention 全局池化局部保留,CCA-Attention为LLM长文本建模带来突破性进展 琶洲实验室、华南理工大学联合推出关键上下文感知注意力机制(CCA-Attention),…...

树莓派超全系列教程文档--(61)树莓派摄像头高级使用方法
树莓派摄像头高级使用方法 配置通过调谐文件来调整相机行为 使用多个摄像头安装 libcam 和 rpicam-apps依赖关系开发包 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 配置 大多数用例自动工作,无需更改相机配置。但是,一…...

mongodb源码分析session执行handleRequest命令find过程
mongo/transport/service_state_machine.cpp已经分析startSession创建ASIOSession过程,并且验证connection是否超过限制ASIOSession和connection是循环接受客户端命令,把数据流转换成Message,状态转变流程是:State::Created 》 St…...

iPhone密码忘记了办?iPhoneUnlocker,iPhone解锁工具Aiseesoft iPhone Unlocker 高级注册版分享
平时用 iPhone 的时候,难免会碰到解锁的麻烦事。比如密码忘了、人脸识别 / 指纹识别突然不灵,或者买了二手 iPhone 却被原来的 iCloud 账号锁住,这时候就需要靠谱的解锁工具来帮忙了。Aiseesoft iPhone Unlocker 就是专门解决这些问题的软件&…...

鱼香ros docker配置镜像报错:https://registry-1.docker.io/v2/
使用鱼香ros一件安装docker时的https://registry-1.docker.io/v2/问题 一键安装指令 wget http://fishros.com/install -O fishros && . fishros出现问题:docker pull 失败 网络不同,需要使用镜像源 按照如下步骤操作 sudo vi /etc/docker/dae…...
-HIve数据分析)
大数据学习(132)-HIve数据分析
🍋🍋大数据学习🍋🍋 🔥系列专栏: 👑哲学语录: 用力所能及,改变世界。 💖如果觉得博主的文章还不错的话,请点赞👍收藏⭐️留言Ǵ…...

OPenCV CUDA模块图像处理-----对图像执行 均值漂移滤波(Mean Shift Filtering)函数meanShiftFiltering()
操作系统:ubuntu22.04 OpenCV版本:OpenCV4.9 IDE:Visual Studio Code 编程语言:C11 算法描述 在 GPU 上对图像执行 均值漂移滤波(Mean Shift Filtering),用于图像分割或平滑处理。 该函数将输入图像中的…...

Java + Spring Boot + Mybatis 实现批量插入
在 Java 中使用 Spring Boot 和 MyBatis 实现批量插入可以通过以下步骤完成。这里提供两种常用方法:使用 MyBatis 的 <foreach> 标签和批处理模式(ExecutorType.BATCH)。 方法一:使用 XML 的 <foreach> 标签ÿ…...

基于 TAPD 进行项目管理
起因 自己写了个小工具,仓库用的Github。之前在用markdown进行需求管理,现在随着功能的增加,感觉有点难以管理了,所以用TAPD这个工具进行需求、Bug管理。 操作流程 注册 TAPD,需要提供一个企业名新建一个项目&#…...
