非盲去模糊简单介绍
文章目录
- 非盲去模糊简单介绍
- 基于频域的方法
- 1. Wiener滤波器
- 2. 逆滤波器和半正定滤波器
- 基于空域的方法
- 1. 均值滤波器
- 2. 高斯滤波器
- 3. 双边滤波器
- 基于偏微分的方法
- 1. 非线性扩散滤波
- 2. 全变分模型
- 3. Laplacian正则化模型
- 振铃效应
- 应用
- 总结
非盲去模糊简单介绍
非盲去模糊是一种通过对图像进行处理,去除由模糊引起的失真的方法。在图像处理中,模糊通常是由于图像在成像过程中受到了光学系统、传感器和运动模糊等因素的影响所产生的。这些因素会导致图像的细节信息受到破坏,从而影响图像的质量。非盲去模糊的主要思路是在已知模糊函数的情况下,对图像进行处理,从而恢复原始图像。
本文将介绍三种常见的非盲去模糊方法:基于频域的方法、基于空域的方法和基于偏微分的方法。最后说一下振铃效应。
基于频域的方法
基于频域的非盲去模糊方法主要利用图像和模糊函数的傅里叶变换,在频域中对图像进行滤波或者修正,然后再进行逆傅里叶变换得到恢复后的图像。
常见的基于频域的非盲去模糊方法包括:
1. Wiener滤波器
Wiener滤波器是一种基于频域的去模糊方法,它通过在频域中对图像进行滤波,从而恢复原始图像。Wiener滤波器的公式为:
H w ( u , v ) = 1 H ( u , v ) ∣ H ( u , v ) ∣ 2 ∣ H ( u , v ) ∣ 2 + K H_{w}(u, v) = \frac{1}{H(u, v)} \frac{|H(u, v)|^2}{|H(u, v)|^2 + K} Hw(u,v)=H(u,v)1∣H(u,v)∣2+K∣H(u,v)∣2
其中, H ( u , v ) H(u, v) H(u,v) 表示模糊函数在频域中的表示, H w ( u , v ) H_w(u, v) Hw(u,v) 表示Wiener滤波器在频域中的表示, K K K 是一个常数,用于控制滤波器的强度。
2. 逆滤波器和半正定滤波器
逆滤波器和半正定滤波器也是基于频域的非盲去模糊方法。它们的基本思想是将经过模糊的图像在频域中与模糊函数的逆滤波器或半正定滤波器进行相乘,得到一个未经过模糊的频域图像,然后再进行逆傅里叶变换,得到恢复后的图像。
逆滤波器的频域表达式为:
H i n v ( u , v ) = 1 H ( u , v ) H_{inv}(u,v) = \frac{1}{H(u,v)} Hinv(u,v)=H(u,v)1
半正定滤波器的频域表达式为:
H p ( u , v ) = { 1 H ( u , v ) ∣ H ( u , v ) ∣ 2 ≥ T 0 otherwise H_{p}(u,v) = \begin{cases} \frac{1}{H(u,v)} \quad |H(u,v)|^2 \geq T \\ 0 \quad \text{otherwise} \end{cases} Hp(u,v)={H(u,v)1∣H(u,v)∣2≥T0otherwise
其中, T T T 是一个阈值,用于控制滤波器的强度。
基于空域的方法
基于空域的非盲去模糊方法主要是通过在图像的空域中进行滤波或者修正来去除噪声和模糊。
常见的基于空域的非盲去模糊方法包括:
1. 均值滤波器
均值滤波器是一种基于空域的去模糊方法,它通过对图像中每个像素周围的像素进行平均,从而去除噪声和模糊。
2. 高斯滤波器
高斯滤波器是一种基于空域的去模糊方法,它通过对图像进行高斯滤波,从而降低图像中的高频噪声和模糊。
3. 双边滤波器
双边滤波器是一种基于空域的去模糊方法,它通过对图像进行双边滤波,从而去除噪声和模糊。双边滤波器不仅考虑像素之间的空间距离,还考虑像素之间的灰度差异。
基于偏微分的方法
基于偏微分的非盲去模糊方法主要利用偏微分方程来描述图像的演化过程,通过不断迭代求解偏微分方程,最终得到恢复后的图像。
常见的基于偏微分的非盲去模糊方法包括:
1. 非线性扩散滤波
非线性扩散滤波是一种基于偏微分方程的非线性方法,它的主要思想是通过调整图像的梯度来达到去噪或者去模糊的目的。
非线性扩散滤波的偏微分方程可以写成如下形式:
∂ u ( x , y , t ) ∂ t = ∇ ⋅ ( g ( ∣ ∇ u ( x , y , t ) ∣ 2 ) ⋅ ∇ u ( x , y , t ) ) \frac{\partial u(x,y,t)}{\partial t} = \nabla \cdot (g(|\nabla u(x,y,t)|^2) \cdot \nabla u(x,y,t)) ∂t∂u(x,y,t)=∇⋅(g(∣∇u(x,y,t)∣2)⋅∇u(x,y,t))
其中, u ( x , y , t ) u(x,y,t) u(x,y,t) 表示时刻 t t t 时的图像, g ( ∣ ∇ u ( x , y , t ) ∣ 2 ) g(|\nabla u(x,y,t)|^2) g(∣∇u(x,y,t)∣2) 表示一个非线性函数,它的作用是根据图像的梯度大小来调整扩散系数,从而达到去噪或者去模糊的目的。
非线性扩散滤波的优点是能够很好地保留图像的边缘和纹理等细节信息,在处理含有大量噪声的图像时表现出色。但它也存在一些缺点,例如处理大尺度的图像时需要耗费大量的计算资源,并且在处理低频信息时可能会出现失真等问题。
2. 全变分模型
全变分模型是一种基于偏微分方程的非线性方法,它的主要思想是通过最小化图像的边缘总变分来达到去噪或者去模糊的目的。
全变分模型的偏微分方程可以写成如下形式:
∂ u ( x , y , t ) ∂ t = div ( ∇ u ( x , y , t ) ∣ ∇ u ( x , y , t ) ∣ ) \frac{\partial u(x,y,t)}{\partial t} = \operatorname{div} \left(\frac{\nabla u(x,y,t)}{|\nabla u(x,y,t)|}\right) ∂t∂u(x,y,t)=div(∣∇u(x,y,t)∣∇u(x,y,t))
其中, u ( x , y , t ) u(x,y,t) u(x,y,t) 表示时刻 t t t 时的图像, div \operatorname{div} div 表示散度算子, ∣ ∇ u ( x , y , t ) ∣ |\nabla u(x,y,t)| ∣∇u(x,y,t)∣ 表示图像的梯度大小。
全变分模型的优点是能够很好地保留图像的边缘和纹理等细节信息,在处理含有大量噪声的图像时表现出色。但它也存在一些缺点,例如处理大尺度的图像时需要耗费大量的计算资源,并且在处理低频信息时可能会出现失真等问题。
3. Laplacian正则化模型
Laplacian正则化模型是一种基于偏微分方程的非线性方法,它的主要思想是通过调整图像的二阶导数来达到去噪或者去模糊的目的。
Laplacian正则化模型的偏微分方程可以写成如下形式:
∂ u ( x , y , t ) ∂ t = ∇ ⋅ ( λ ∇ 2 u ( x , y , t ) ) \frac{\partial u(x,y,t)}{\partial t} = \nabla \cdot (\lambda \nabla^2 u(x,y,t)) ∂t∂u(x,y,t)=∇⋅(λ∇2u(x,y,t))
其中, u ( x , y , t ) u(x,y,t) u(x,y,t) 表示时刻 t t t 时的图像, ∇ 2 \nabla^2 ∇2 表示图像的二阶导数算子, λ \lambda λ 表示正则化参数。
Laplacian正则化模型的优点是能够很好地保留图像的边缘和纹理等细节信息,在处理含有大量噪声的图像时表现出色。但它也存在一些缺点,例如处理大尺度的图像时需要耗费大量的计算资源,并且在处理低频信息时可能会出现失真等问题。
总之,基于偏微分的图像去模糊方法有很多种,选择何种方法应该根据具体的应用需求和图像特征来进行选择。
振铃效应
振铃效应是指在图像去模糊过程中,由于卷积核的截断或过窄等原因,导致图像出现高频振荡的现象。这种现象会使得图像看起来更加模糊,从而降低了图像的质量。振铃效应一般是由于去模糊算法中的高通滤波器引起的。
在去模糊处理时,我们通常会使用高通滤波器来增强图像的高频细节,从而使得图像变得更加清晰。然而,高通滤波器会增加图像的高频分量,这会导致细节过多,从而使得图像边缘周围出现环带或者震荡。另外,振铃效应还与图像采样和重建有关。
为了减轻振铃效应的影响,我们可以采用一些技术手段。例如,可以使用低通滤波器来降低高频信息的幅值,或者使用特定的去模糊算法来减少振铃效应。另外,增加采样率和使用更高质量的重建算法也可以减轻振铃效应。需要注意的是,这些技术手段也可能会降低图像的清晰度和细节,因此需要根据实际情况进行调整。
振铃效应通常可以通过增加卷积核的大小或者在卷积之前对卷积核进行平滑的方式进行缓解。另外,使用一些特殊的卷积核,比如高斯卷积核、拉普拉斯卷积核等,也可以减轻振铃效应的影响。此外,一些基于深度学习的图像去模糊方法也可以通过训练深度神经网络来学习去除振铃效应的方法。
总之,振铃效应是图像去模糊过程中常见的问题之一,它会使得图像出现高频振荡的现象,从而降低了图像的质量。为了缓解振铃效应的影响,可以使用一些特殊的卷积核、增加卷积核的大小、使用低通滤波器等方法。同时,需要根据实际情况进行技术手段的选择和调整。
应用
非盲去模糊在许多领域都有着广泛的应用,例如医学图像处理、无人驾驶汽车、视频监控等等。在这些应用中,非盲去模糊可以帮助我们还原原始场景中的细节和清晰度,提高图像质量和准确性,从而更好地满足实际需求。
总结
以上是三种常见的非盲去模糊方法:基于频域的方法、基于空域的方法和基于偏微分的方法。不同的方法适用于不同的场景,选择合适的方法能够得到更好的去模糊效果。在实际应用中,通常需要根据具体情况选择合适的去模糊方法。在应用过程中,需要注意振铃效应的问题,并采取相应的措施来解决。
相关文章:

非盲去模糊简单介绍
文章目录 非盲去模糊简单介绍基于频域的方法1. Wiener滤波器2. 逆滤波器和半正定滤波器 基于空域的方法1. 均值滤波器2. 高斯滤波器3. 双边滤波器 基于偏微分的方法1. 非线性扩散滤波2. 全变分模型3. Laplacian正则化模型 振铃效应应用总结 非盲去模糊简单介绍 非盲去模糊是一…...

C语言动态内存管理与文件操作:打造高效通讯录
本篇博客会讲解如何使用C语言实现一个通讯录。实现通讯录的过程中,会大量用到C语言的知识点,包括但不限于:函数、自定义类型、指针、动态内存管理、文件操作,这些知识点在我的其他博客中都有讲解过,欢迎大家阅读&#…...
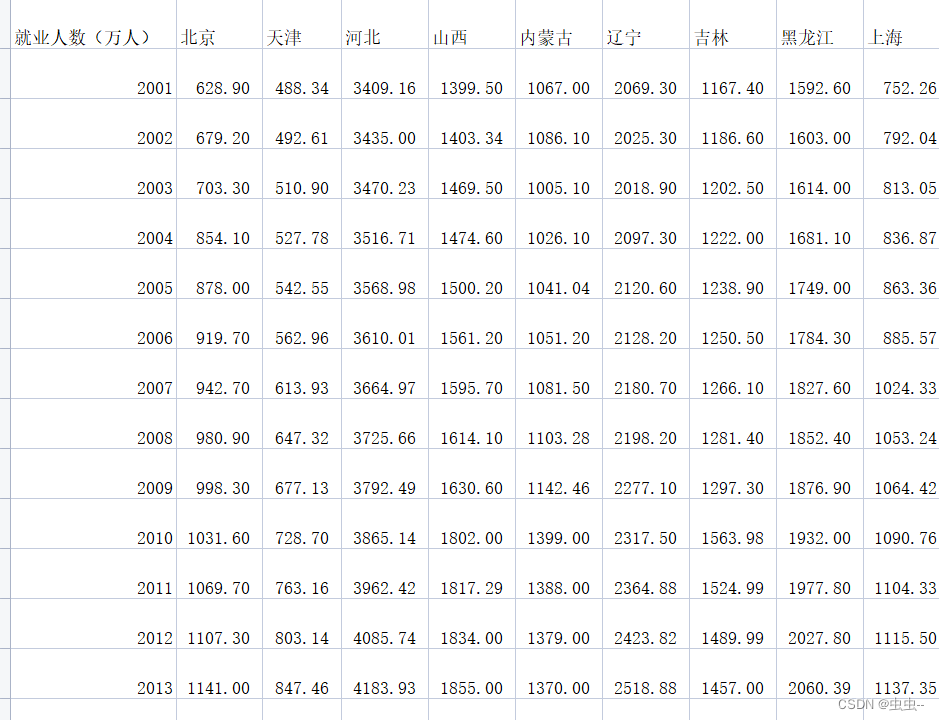
2001-2021年全国30省就业人数数据
2001-2021年全国30省就业人数数据/各省就业人数数据 1、时间:2001-2021年 2、范围:包括30个省市不含西藏 3、指标:就业人数 4、来源:各省NJ、社会统计NJ 5、缺失情况说明:无缺失 6、指标说明: 就业人…...

自然语言处理知识抽取(pkuseg、DDParser安装及使用)
一、分词简介 1.基本概念 分词是自然语言处理中的一个重要步骤,它可以帮助我们将文本分成一个个词语,以便更好地理解和分析文本。在计算机视觉、语音识别、机器翻译等领域,分词都扮演着重要的角色。 目前,常用的分词库包括 jie…...

Linux内核面试知识总结
Linux启动过程 1、主机加电自检,加载BIOS硬件信息 2、读取MBR引导文件 3、引导linux内核 4、启动第一个进程init(进程号永远为1) 5、进度相应的运行级别 6、运行终端,输入用户名和密码 linux系统缺省的运行级别 关机、单机…...
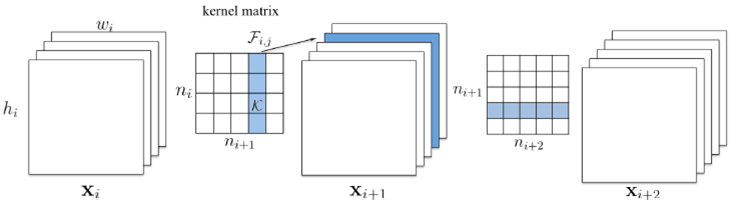
深度学习模型压缩与优化加速
1. 简介 深度学习(Deep Learning)因其计算复杂度或参数冗余,在一些场景和设备上限制了相应的模型部署,需要借助模型压缩、系统优化加速、异构计算等方法突破瓶颈,即分别在算法模型、计算图或算子优化以及硬件加速等层…...

Kali 更换源(超详细,附国内优质镜像源地址)
1.进入管理员下的控制台。 2. 输入密码后点击“授权”。 3.在控制台内输入下面的内容。 vim /etc/apt/sources.list 4.敲击回车后会进入下面的页面。 5.来到这个页面后的第一部是按键盘上的“i”键,左下角出现“插入”后说明操作正确。 6.使用“#”将原本的源给注释…...

Java版工程项目管理系统平台+java版企业工程系统源码+助力工程企业实现数字化管理
Java版工程项目管理系统 Spring CloudSpring BootMybatisVueElementUI前后端分离 功能清单如下: 首页 工作台:待办工作、消息通知、预警信息,点击可进入相应的列表 项目进度图表:选择(总体或单个)项目显示1…...
搜索引擎测试报告
文章目录 一、项目背景二、项目功能三、测试目的四、测试环境五、测试计划1、功能测试2、自动化测试 六、测试结果 一、项目背景 java官方文档是我们在学习java语言中不可或缺的权威资料。相比于各种网站的Java资料,官方文档无论是语言表达还是组织方式都要更加全面…...

4年的测试工程师,你遇到过自身瓶颈期吗?又是怎样度过的?
从毕业到现在已经快4年啦,一直软件测试行业混迹。我不是牛人,但是自我感觉还算是个合格的测试工程师,有必要写下自己将近4年来的经历,给自我以提示,给刚入行的朋友提供点参考。 貌似这一点适应的行业最广,…...

【Python零基础学习入门篇④】——第四节:Python的列表、元组、集合和字典
⬇️⬇️⬇️⬇️⬇️⬇️ ⭐⭐⭐Hello,大家好呀我是陈童学哦,一个普通大一在校生,请大家多多关照呀嘿嘿😁😊😘 🌟🌟🌟技术这条路固然很艰辛,但既已选择&…...

3.6 cache存储器
学习步骤: 我会采取以下几个步骤来学习Cache存储器: 确定学习目标:Cache存储器作为一种高速缓存存储器,通常用于提高计算机系统的运行效率。因此,我需要明确学习Cache存储器的目的,包括了解其原理、结构和…...
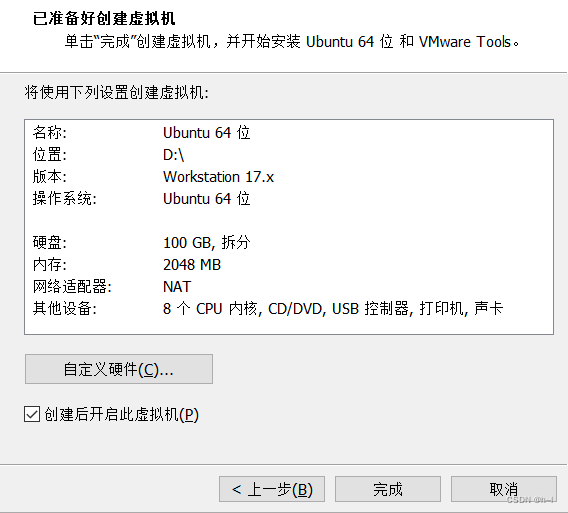
Ubuntu零基础安装
Ubuntu零基础安装 首先我们需要安装VM,再安装ubuntu。 1、安装VM 进入VM官网 VM官网地址 选择下载试用版 下载Windows版本 下载完成后,点击安装包进行安装 至此就安装完毕了。 桌面会出现VM的图标。 点击打开,弹出如下画面: …...

热门的常用 API 大全分享
天气/环境 空气质量查询: 查询国内3400个城市的整点观测,获取指定城市的整点观测空气质量。未来7天生活指数:支持国内3400个城市以及国际4万个城市的天气指数数据,包括晨练、洗车、穿衣(12项,有详细说明&a…...
利用粒子群算法设计无线传感器网络中的最优安全路由模型(Matlab代码实现)
目录 💥1 概述 📚2 运行结果 🎉3 参考文献 👨💻4 Matlab代码 💥1 概述 无线传感器网络(WSN)由数十个、数百个甚至数千个自主传感器组成。这些传感器以无线方式嵌入环境中&…...

2023年华东杯数学建模B 题 期货价格相关性问题-思路解析
题目背景: 许多金融标的都有其内在的关联,如何从量价数据找到这种关联是一个有趣的 问题。例如在万得的“煤焦钢矿”板块中,有螺纹钢、铁矿石、不锈钢、热轧卷板、 硅铁、焦煤、焦炭、锰硅、线材 9 个品种。这些品种有些是上下游关系&…...
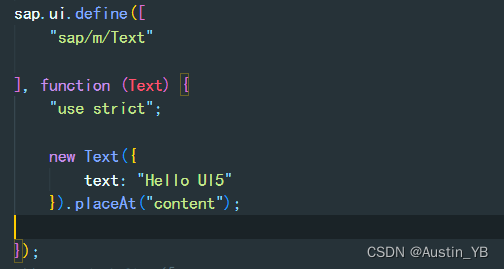
SAP UI5 之Controls (控件) 笔记三
文章目录 官网 Walkthrough学习-Controls控件1.0.1 在index.html中使用class id 属性控制页面展示的属性1.0.2 我们在index.js文件中引入 text文本控制1.0.3打开浏览器查看结果 官网 Walkthrough学习-Controls控件 Controls控件 在前面展示在浏览器中的Hello World 是在Html …...

哈希表题目:设计地铁系统
文章目录 题目标题和出处难度题目描述要求示例数据范围 解法思路和算法代码复杂度分析 题目 标题和出处 标题:设计地铁系统 出处:1396. 设计地铁系统 难度 6 级 题目描述 要求 一个地铁系统正在收集乘客在不同站之间的花费时间。他们在使用这些数…...
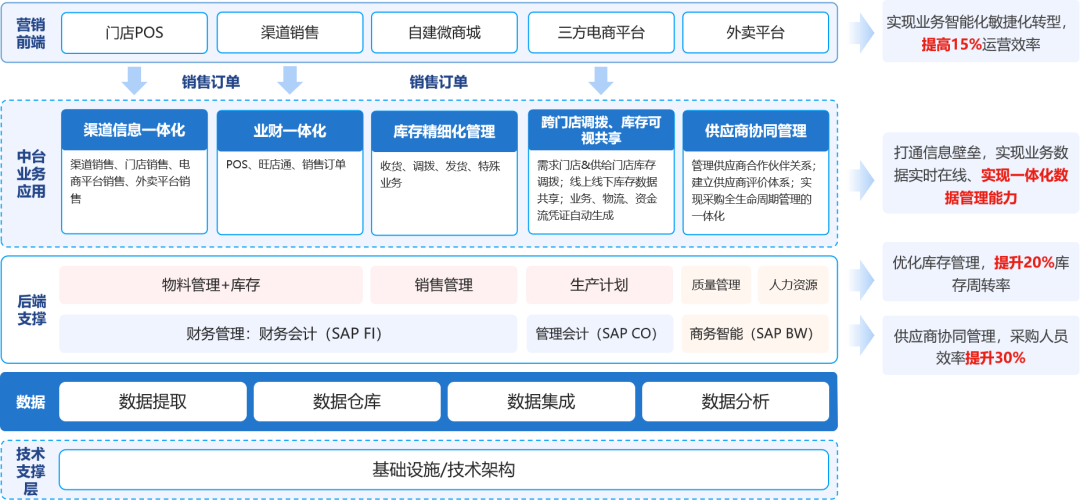
云时通OMS:为零售品牌商打造高效的全渠道订单管理!
传统的零售企业围绕“人、货、场” 三要素来展开营销,其目标是基于“场”将货销售给更多的人。随着数字技术的应用,新零售模式下的“场”除了传统的线下店铺外,还拓展了多元化的线上渠道,比如小程序、企业APP、第三方平台、电商直…...

有必要给孩子买台灯吗?分享四款高品质的护眼台灯
有必要使用护眼台灯,尤其是有近视现象的孩子们。 现在很多孩子小学就开始近视了,保护视力刻不容缓呀! 很多人不知道,其实劣质光线是最大的眼睛杀手 给孩子随便买便宜的台灯,看着一样能用,其实时间久了 对孩子眼睛的…...

内存分配函数malloc kmalloc vmalloc
内存分配函数malloc kmalloc vmalloc malloc实现步骤: 1)请求大小调整:首先,malloc 需要调整用户请求的大小,以适应内部数据结构(例如,可能需要存储额外的元数据)。通常,这包括对齐调整,确保分配的内存地址满足特定硬件要求(如对齐到8字节或16字节边界)。 2)空闲…...

python/java环境配置
环境变量放一起 python: 1.首先下载Python Python下载地址:Download Python | Python.org downloads ---windows -- 64 2.安装Python 下面两个,然后自定义,全选 可以把前4个选上 3.环境配置 1)搜高级系统设置 2…...

屋顶变身“发电站” ,中天合创屋面分布式光伏发电项目顺利并网!
5月28日,中天合创屋面分布式光伏发电项目顺利并网发电,该项目位于内蒙古自治区鄂尔多斯市乌审旗,项目利用中天合创聚乙烯、聚丙烯仓库屋面作为场地建设光伏电站,总装机容量为9.96MWp。 项目投运后,每年可节约标煤3670…...

数据库分批入库
今天在工作中,遇到一个问题,就是分批查询的时候,由于批次过大导致出现了一些问题,一下是问题描述和解决方案: 示例: // 假设已有数据列表 dataList 和 PreparedStatement pstmt int batchSize 1000; // …...

python报错No module named ‘tensorflow.keras‘
是由于不同版本的tensorflow下的keras所在的路径不同,结合所安装的tensorflow的目录结构修改from语句即可。 原语句: from tensorflow.keras.layers import Conv1D, MaxPooling1D, LSTM, Dense 修改后: from tensorflow.python.keras.lay…...

深入浅出深度学习基础:从感知机到全连接神经网络的核心原理与应用
文章目录 前言一、感知机 (Perceptron)1.1 基础介绍1.1.1 感知机是什么?1.1.2 感知机的工作原理 1.2 感知机的简单应用:基本逻辑门1.2.1 逻辑与 (Logic AND)1.2.2 逻辑或 (Logic OR)1.2.3 逻辑与非 (Logic NAND) 1.3 感知机的实现1.3.1 简单实现 (基于阈…...

6️⃣Go 语言中的哈希、加密与序列化:通往区块链世界的钥匙
Go 语言中的哈希、加密与序列化:通往区块链世界的钥匙 一、前言:离区块链还有多远? 区块链听起来可能遥不可及,似乎是只有密码学专家和资深工程师才能涉足的领域。但事实上,构建一个区块链的核心并不复杂,尤其当你已经掌握了一门系统编程语言,比如 Go。 要真正理解区…...

[特殊字符] 手撸 Redis 互斥锁那些坑
📖 手撸 Redis 互斥锁那些坑 最近搞业务遇到高并发下同一个 key 的互斥操作,想实现分布式环境下的互斥锁。于是私下顺手手撸了个基于 Redis 的简单互斥锁,也顺便跟 Redisson 的 RLock 机制对比了下,记录一波,别踩我踩过…...

简约商务通用宣传年终总结12套PPT模版分享
IOS风格企业宣传PPT模版,年终工作总结PPT模版,简约精致扁平化商务通用动画PPT模版,素雅商务PPT模版 简约商务通用宣传年终总结12套PPT模版分享:商务通用年终总结类PPT模版https://pan.quark.cn/s/ece1e252d7df...

Android Framework预装traceroute执行文件到system/bin下
文章目录 Android SDK中寻找traceroute代码内置traceroute到SDK中traceroute参数说明-I 参数(使用 ICMP Echo 请求)-T 参数(使用 TCP SYN 包) 相关文章 Android SDK中寻找traceroute代码 设备使用的是Android 11,在/s…...
