机器学习:多项式拟合分析中国温度变化与温室气体排放量的时序数据
文章目录
- 1、前言
- 2、定义及公式
- 3、案例代码
- 1、数据解析
- 2、绘制散点图
- 3、多项式回归、拟合
- 4、注意事项
1、前言
当分析数据时,如果我们找的不是直线或者超平面,而是一条曲线,那么就可以用多项式回归来分析和预测。
2、定义及公式
多项式回归可以写成:
Y i = β 0 + β 1 X i + β 2 X i 2 + . . . + β k X i k Y_{i} = \beta_{0} +\beta_{1}X_{i}+\beta_{2}X_{i}^2+...+\beta_{k}X_{i}^k Yi=β0+β1Xi+β2Xi2+...+βkXik
例如二次曲线:
Y = a X + b X 2 + c Y=aX+bX^2+c Y=aX+bX2+c
3、案例代码
1、数据解析
首先有1961年至2017年我国地表温度变化和温室气体排放量的时间序列数据,前十条数据如下。
| temp | emissions |
|---|---|
| 0.257 | 5635838102 |
| -0.142 | 6075180207 |
| 0.288 | 6510697811 |
| -0.028 | 6946401541 |
| 0.076 | 7421082166 |
| 0.18 | 7942541079 |
| -0.286 | 8374764636 |
| -0.414 | 8842570279 |
| -0.22 | 9418514950 |
2、绘制散点图
对于该数据我们先通过绘制散点图,这可以看出该数据适用于什么模型。
import matplotlib.pyplot as plt
import xlrd
import numpy as np
# 载入数据,打开excel文件
ExcelFile = xlrd.open_workbook("sandian.xls")
sheet1 = ExcelFile.sheet_by_index(0)
x = sheet1.col_values(0)
y = sheet1.col_values(1)
# 将列表转换为matrix
x = np.matrix(x).reshape(48, 1)
y = np.matrix(y).reshape(48, 1)# 划线y
plt.title("Epidemic and Dow Jones data analysis")
plt.xlabel("new cases")
plt.ylabel("Dow Jones Volume")
plt.plot(x, y, 'b.')
plt.show()
上述使用xlrd方式不建议使用,简单了解即可,正常我们会使用下述更为方便且稳定的pandas来读取csv文件,这会大大简洁我们的代码并减少工作量。当然结果也是一样的。
import matplotlib.pyplot as plt
import numpy as np
import pandas as pdx = pd.read_csv('china.csv')['emissions']
y = pd.read_csv('china.csv')['temp']
# 划线y
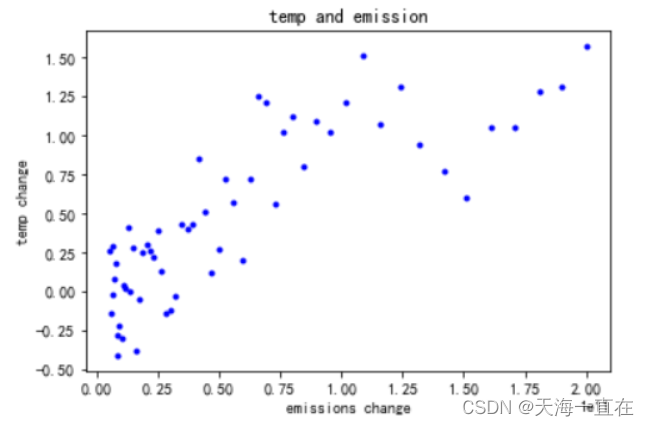
plt.title("temp and emission")
plt.xlabel("emissions change")
plt.ylabel("temp change")
plt.plot(x, y, 'b.')
plt.show()
如图所示很明显,在排放量变化达到1.5(1e11)时,斜率发生了改变,因此我们可以判断这是一个多项式模型。
3、多项式回归、拟合
通过散点图的趋势,我们首先选择拟合3次来防止过拟合和欠拟合。
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
from sklearn.metrics import r2_score
from matplotlib.font_manager import FontProperties # 导入FontPropertiesfont = FontProperties(fname="simhei.ttf", size=14) # 设置字体
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] =Falsex = pd.read_csv('china.csv')['emissions']
y = pd.read_csv('china.csv')['temp']# 进行多项式拟合(这里选取3次多项式拟合)
z = np.polyfit(x, y, 3) # 用3次多项式拟合# 获取拟合后的多项式
p = np.poly1d(z)
print(p) # 在屏幕上打印拟合多项式# 计算拟合后的y值
yvals=p(x)# 计算拟合后的R方,进行检测拟合效果
r2 = r2_score(y, yvals)
print('多项式拟合R方为:', r2)# 计算拟合多项式的极值点。
peak = np.polyder(p, 1)
print(peak.r)# 画图对比分析
plot1 = plt.plot(x, y, '*', label='初始值', color='red')
plot2 = plt.plot(x, yvals, '-', label='训练值', color='blue',linewidth=2)plt.xlabel('温室气体排放量',fontsize=13, fontproperties=font)
plt.ylabel('温度变化',fontsize=13, fontproperties=font)
plt.legend(loc="best")
plt.title('中国温室气体排放量与地表温度变化的关系')
plt.show()
最后结果如下图
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-go17Atvf-1681182766850)(C:\Users\Administrator\AppData\Roaming\Typora\typora-user-images\image-20230411105218629.png)]](https://img-blog.csdnimg.cn/ed3509076d154912a7bd5c19a2223eba.png)
3 2
3.002e-34 x - 1.351e-22 x + 2.284e-11 x - 0.2613
多项式拟合R方为: 0.7468687074304835
[1.50000065e+11+5.34488173e+10j 1.50000065e+11-5.34488173e+10j]
我们发现,这并不符合我们的预期,因为温室气体排放量在1.5(1e11)时,散点图趋势有明显的凹陷,而使用三次拟合并不能让曲线拟合到散点上。所以我们将 z = np.polyfit(x, y, 4)中的3改为4,来进行四次拟合。
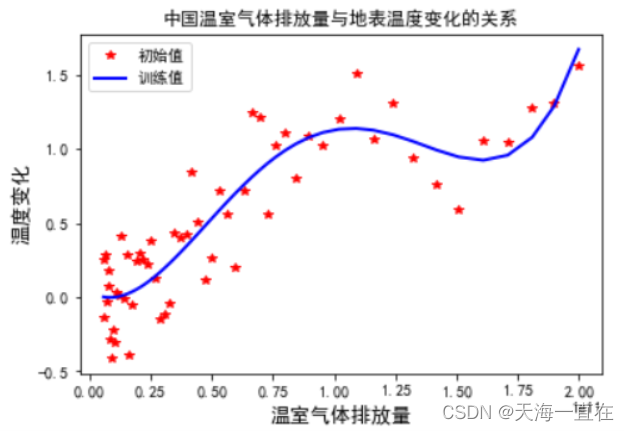
这样就达到了我们的预期效果,并输出我们的多项式回归公式。
4 3 2
1.702e-44 x - 6.273e-33 x + 6.634e-22 x - 9.696e-12 x + 0.03595
多项式拟合R方为: 0.7962406171380259
[1.60734484e+11 1.07514523e+11 8.24309615e+09]
我们可以得到数学模型:
Y = 1.702 ∗ 1 0 − 44 X − 6.273 ∗ 1 0 − 33 X + 6.634 ∗ 1 0 − 22 X − 9.696 ∗ 1 0 − 12 X + 0.03595 Y=1.702*10^{-44}X -6.273*10^{-33}X + 6.634*10^{-22}X-9.696*10^{-12}X +0.03595 Y=1.702∗10−44X−6.273∗10−33X+6.634∗10−22X−9.696∗10−12X+0.03595
4、注意事项
from matplotlib.font_manager import FontProperties # 导入FontProperties
font = FontProperties(fname="simhei.ttf", size=14) # 设置字体
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] =False
这些代码用于显示汉字标题,这需要你的本机中有一个汉字字体文件,simhei.ttf或其他字体文件。
如果需要引入,在第二行中指定文件路径。
相关文章:

机器学习:多项式拟合分析中国温度变化与温室气体排放量的时序数据
文章目录 1、前言2、定义及公式3、案例代码1、数据解析2、绘制散点图3、多项式回归、拟合4、注意事项 1、前言 当分析数据时,如果我们找的不是直线或者超平面,而是一条曲线,那么就可以用多项式回归来分析和预测。 2、定义及公式 多项…...

一个 24 通道 100Msps 逻辑分析仪
这是一个创建非常便宜的逻辑分析仪的项目,但其功能可与昂贵的商业分析仪相媲美。该分析仪可以以每秒 1 亿个样本的最高速度对多达 24 个通道进行采样,并且可以通过单个通道中的极性变化或多达 16 个通道形成的模式来触发。 该项目不仅包含硬件࿰…...

使用Process Explorer和Dependency Walker排查C++程序中dll库动态加载失败问题
目录 1、exe主程序启动时的库加载流程说明 2、加载dll库两种方式 2.1、dll库的隐式引用...
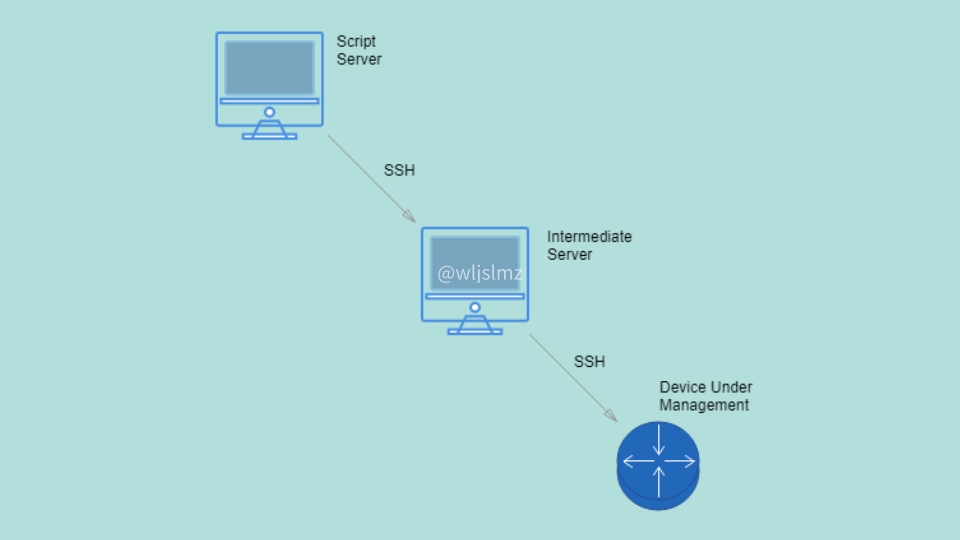
网工Python:如何使用Netmiko的SCP函数进行文件传输?
在网络设备管理中,传输配置文件、镜像文件等是经常需要进行的操作。Netmiko是一个Python库,可用于与各种网络设备进行交互,提供了一些用于传输文件的函数,其中包括SCP(Secure Copy Protocol)函数。本文将介…...
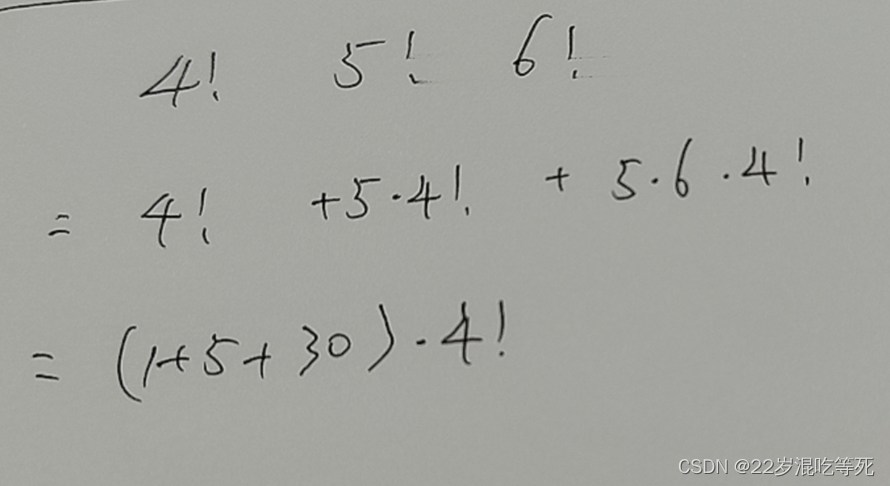
题目 3166: 蓝桥杯2023年第十四届省赛真题-阶乘的和--不能完全通过,最好情况通过67.
原题链接: 题目 3166: 蓝桥杯2023年第十四届省赛真题-阶乘的和 https://www.dotcpp.com/oj/problem3166.html 致歉 害,首先深感抱歉,这道题还是没有找到很好的解决办法。目前最好情况就是67分。 这道题先这样跳过吧,当然以后还…...
 介绍)
ChatGPT- OpenAI 的 模型(Model) 介绍
ChatGPT的火爆程度大家都知道了,该章节我们来了解一下 ChatGPT 一个关键概念 - 模型(Model)。主要是为大家介绍一下在 OpenAI 中,究竟有哪些模型可以使用。 在后续的章节,我们会分单独的小章节逐一的为大家介绍各个不同模型的调用以及接口参…...

X 态及基于 VCS 的 X-Propagation 检测
🔥点击查看精选 IC 技能树系列文章🔥 🔥点击进入【芯片设计验证】社区,查看更多精彩内容🔥 📢 声明: 🥭 作者主页:【MangoPapa的CSDN主页】。⚠️ 本文首发于CSDN&#…...
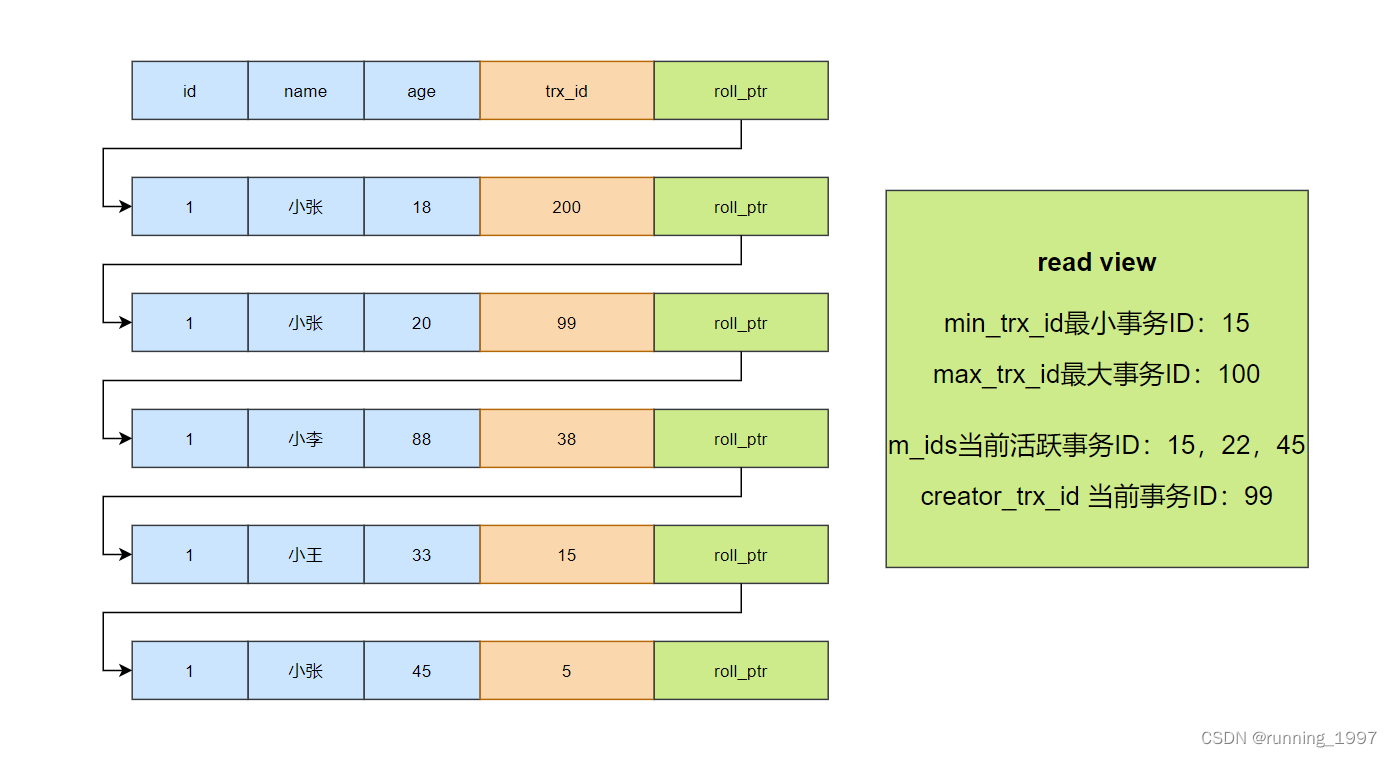
数据库之事务隔离级别详解
事务隔离级别详解 一、事务的四大特性(ACID)1. 原子性(atomicity):2. 一致性(consistency):3. 隔离性(isolation):4. 持久性(durability): 二、事务的四种隔离级别1. 读未提交(Read uncommitted)࿱…...

守护进程、僵尸进程、孤儿进程
守护进程、僵尸进程、孤儿进程 守护进程(Daemon Process) 定义 守护进程又称Daemon进程(精灵进程),是Linux中的后台服务进程。 它的生命周期较长,通常独立于控制终端并且周期性地执行某种任务或者等待处…...
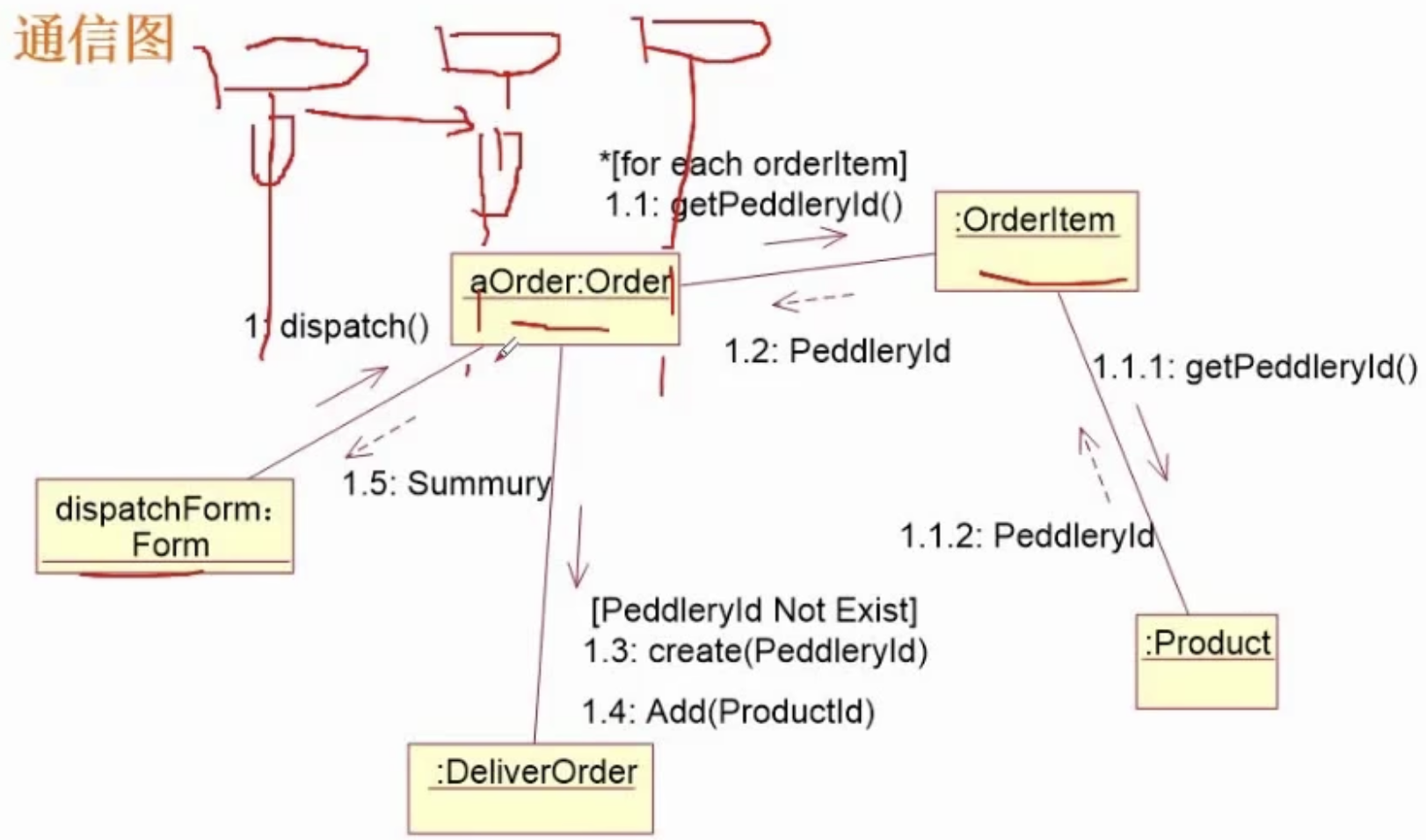
软件设计师笔记
软件设计师笔记 计算机组成与体系结构 数据的表示、计算机结构、Flynn分类法、CISC与RISC、流水线技术、存储系统、总线系统、可靠性、校验码 1. 数据的表示 (一)进制转换 R进制转十进制使用按权展开法: 十进制转R进制使用短除法 二进制…...

4_用dockerfile制作镜像
Docker 镜像原理 思考: Docker 镜像本质是什么? Docker 中一个centos镜像为什么只有200MB,而一个centos操作系统的iso文件要几个个G? Docker 中一个tomcat镜像为什么有500MB,而一个tomcat安装包只有70多MBÿ…...

肝一肝设计模式【四】-- 建造者模式
系列文章目录 肝一肝设计模式【一】-- 单例模式 传送门 肝一肝设计模式【二】-- 工厂模式 传送门 肝一肝设计模式【三】-- 原型模式 传送门 肝一肝设计模式【四】-- 建造者模式 传送门 文章目录 系列文章目录前言一、什么是建造者模式二、举个栗子三、静态内部类写法四、开源框…...
从设计到产品
从设计到产品 最近上的一些课的笔记,从 0 开始设计项目的角度去看产品。 设计系统 设计系统(design system) 不是 系统设计(system design),前者更偏向于 UI/UX 设计部分,后者更偏向于实现部分。 个人觉得,前端开发与 UI/UX 设…...

《疯狂Python讲义》值传递的细节
函数的参数包含着整个程序的规范性,之前还是没有那么去注意重要的细节,读完书中函数值传递篇章,还是有所收获的。 参数有两种形式,一种是形参一种是实参,形参可以理解为实参的载体,函数当中的关键词也是描…...
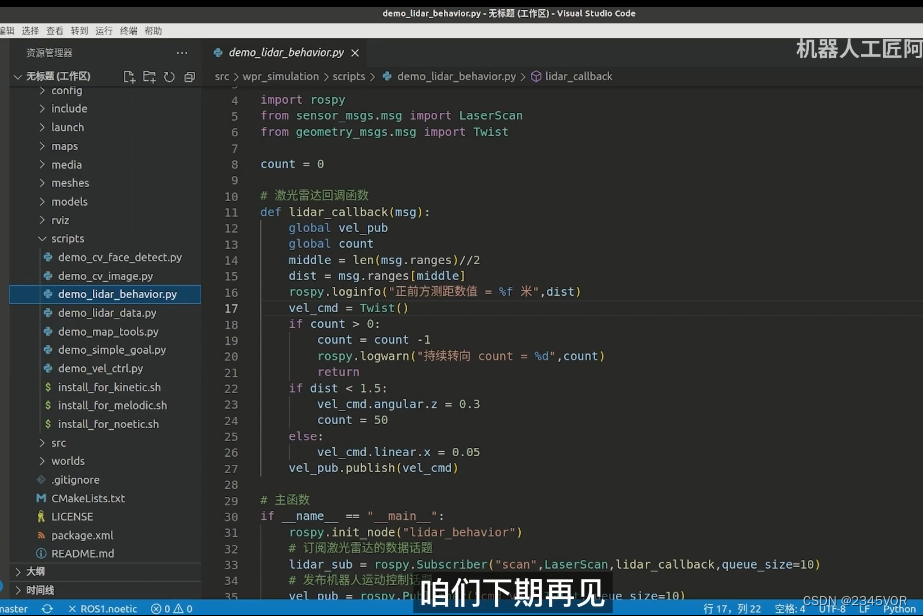
【7. ROS 中的 IMU 惯性测量单元消息包】
欢迎大家阅读2345VOR的博客【6. 激光雷达接入ROS】🥳🥳🥳 2345VOR鹏鹏主页: 已获得CSDN《嵌入式领域优质创作者》称号👻👻👻,座右铭:脚踏实地,仰望星空&#…...

pcie m.2固态硬盘装机后无法识别到启动盘
1、第一种情况《系统版本过低》 原因: 使用m.2固态硬盘的电脑,最好安装iwn8.1以上的系统,因为win7系统及其win xp系统 没有自带NVME驱动。 搞定办法: 比较简单的方式就是直接开运行快启动u盘启动盘制作工具将系统升级到win10系…...

Java Web应用开发 ——第四章:JavaBean技术测验
一.单项选择题(共13题,55.9分) 1 在 JSP 中调用 JavaBean 时不会用到的标记是:( ) A、 < jsp:javabean> B、 < jsp:useBean> C、 < jsp:setProperty> D、 < jsp:getProperty> 正确答案&a…...

CTF权威指南 笔记 -第二章二进制文件- 2.4 -动态链接
目录 静态文件的缺点 动态链接 位置无关代码 延迟绑定 _dl_runtime_reslove 函数定义 深入审视 静态文件的缺点 随着可执行文件的增加 静态链接带来的浪费空间问题就会愈发严重 如果大部分可执行文件都需要glibc 那么在链接的时候就需要把 libc.a链接进去 如果一个libc…...
C++:计算机操作系统:多线程:高并发中的线程
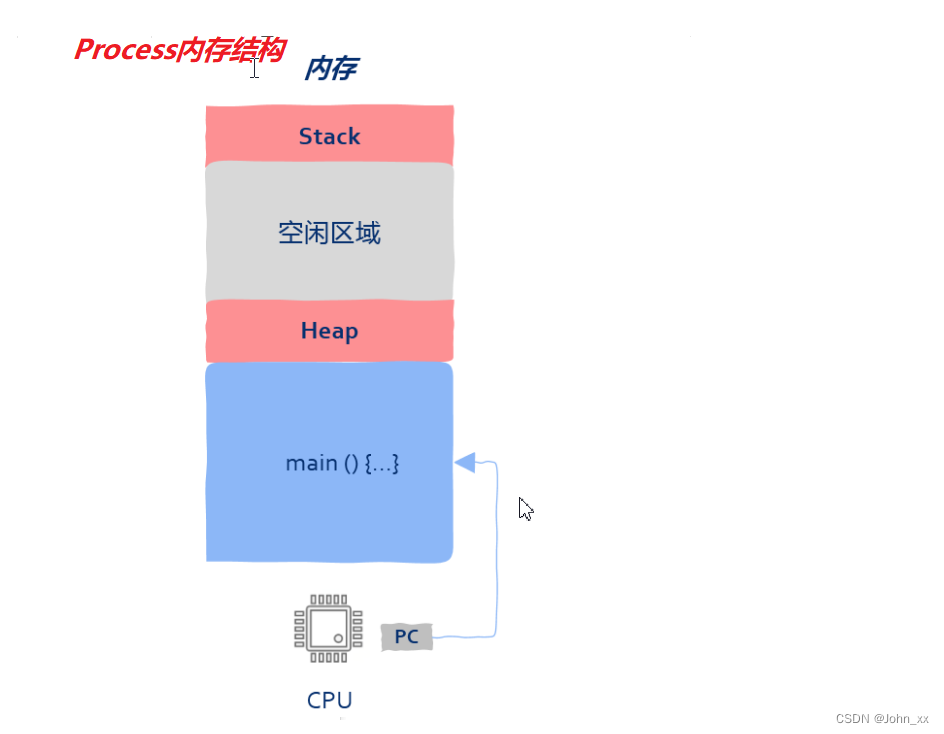
高并发中的线程 一切要从CPU说起PC 程序计数器从CPU到操作系统从进程到线程 从这篇开始,我将会开启高性能,高并发系列,本篇是给系列的开篇,主要关注 多线程以及线程池。 一切要从CPU说起 你可能会有疑问,讲多线程为何…...

大数据Doris(十一):Aggregate 数据模型
文章目录 Aggregate 数据模型 一、导入数据聚合 二、保留明细数据...

Docker 离线安装指南
参考文章 1、确认操作系统类型及内核版本 Docker依赖于Linux内核的一些特性,不同版本的Docker对内核版本有不同要求。例如,Docker 17.06及之后的版本通常需要Linux内核3.10及以上版本,Docker17.09及更高版本对应Linux内核4.9.x及更高版本。…...

CTF show Web 红包题第六弹
提示 1.不是SQL注入 2.需要找关键源码 思路 进入页面发现是一个登录框,很难让人不联想到SQL注入,但提示都说了不是SQL注入,所以就不往这方面想了 先查看一下网页源码,发现一段JavaScript代码,有一个关键类ctfs…...

基于FPGA的PID算法学习———实现PID比例控制算法
基于FPGA的PID算法学习 前言一、PID算法分析二、PID仿真分析1. PID代码2.PI代码3.P代码4.顶层5.测试文件6.仿真波形 总结 前言 学习内容:参考网站: PID算法控制 PID即:Proportional(比例)、Integral(积分&…...

模型参数、模型存储精度、参数与显存
模型参数量衡量单位 M:百万(Million) B:十亿(Billion) 1 B 1000 M 1B 1000M 1B1000M 参数存储精度 模型参数是固定的,但是一个参数所表示多少字节不一定,需要看这个参数以什么…...

基于当前项目通过npm包形式暴露公共组件
1.package.sjon文件配置 其中xh-flowable就是暴露出去的npm包名 2.创建tpyes文件夹,并新增内容 3.创建package文件夹...

uniapp中使用aixos 报错
问题: 在uniapp中使用aixos,运行后报如下错误: AxiosError: There is no suitable adapter to dispatch the request since : - adapter xhr is not supported by the environment - adapter http is not available in the build 解决方案&…...

Mac下Android Studio扫描根目录卡死问题记录
环境信息 操作系统: macOS 15.5 (Apple M2芯片)Android Studio版本: Meerkat Feature Drop | 2024.3.2 Patch 1 (Build #AI-243.26053.27.2432.13536105, 2025年5月22日构建) 问题现象 在项目开发过程中,提示一个依赖外部头文件的cpp源文件需要同步,点…...

Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习)
Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习) 一、Aspose.PDF 简介二、说明(⚠️仅供学习与研究使用)三、技术流程总览四、准备工作1. 下载 Jar 包2. Maven 项目依赖配置 五、字节码修改实现代码&#…...

论文笔记——相干体技术在裂缝预测中的应用研究
目录 相关地震知识补充地震数据的认识地震几何属性 相干体算法定义基本原理第一代相干体技术:基于互相关的相干体技术(Correlation)第二代相干体技术:基于相似的相干体技术(Semblance)基于多道相似的相干体…...

Git常用命令完全指南:从入门到精通
Git常用命令完全指南:从入门到精通 一、基础配置命令 1. 用户信息配置 # 设置全局用户名 git config --global user.name "你的名字"# 设置全局邮箱 git config --global user.email "你的邮箱example.com"# 查看所有配置 git config --list…...
