( 数组和矩阵) 378. 有序矩阵中第 K 小的元素 ——【Leetcode每日一题】
❓378. 有序矩阵中第 K 小的元素
难度:中等
给你一个 n x n n x n nxn 矩阵 m a t r i x matrix matrix ,其中每行和每列元素均按升序排序,找到矩阵中第 k 小的元素。
请注意,它是 排序后 的第 k 小元素,而不是第 k 个 不同 的元素。
你必须找到一个内存复杂度优于 O ( n 2 ) O(n^2) O(n2) 的解决方案。
示例 1:
输入:matrix = [[1,5,9],[10,11,13],[12,13,15]], k = 8
输出:13
解释:矩阵中的元素为 [1,5,9,10,11,12,13,13,15],第 8 小元素是 13
示例 2:
输入:matrix = [[-5]], k = 1
输出:-5
提示:
- n == matrix.length
- n == matrix[i].length
- 1 <= n <= 300
- − 1 0 9 < = m a t r i x [ i ] [ j ] < = 1 0 9 -10^9 <= matrix[i][j] <= 10^9 −109<=matrix[i][j]<=109
- 题目数据 保证 matrix 中的所有行和列都按 非递减顺序 排列
- 1 < = k < = n 2 1 <= k <= n^2 1<=k<=n2
进阶:
- 你能否用一个恒定的内存(即 O ( 1 ) O(1) O(1) 内存复杂度)来解决这个问题?
- 你能在 O ( n ) O(n) O(n) 的时间复杂度下解决这个问题吗?这个方法对于面试来说可能太超前了,但是你会发现阅读这篇文章(
this paper)很有趣。
💡思路:
法一:二分查找
找出二维矩阵中最小的数 l,最大的数 h,我们取中位数 mid = (l + h) / 2,在二维矩阵中寻找小于等于 mid 的元素个数cnt:
- 若这个
cnt小于k,表明第k小的数在右半部分且不包含mid,即l = mid + 1,h不变; - 若这个
cnt大于等于k,表明第k小的数在左半部分且可能包含mid,即l不变,h = mid - 1; - 当
l > h时,第k小的数即被找出,等于l。
法二:归并排序
由题目给出的性质可知,这个矩阵的每一行均为一个有序数组。问题即转化为从这 n 个有序数组中找第 k 大的数,可以想到利用归并排序的做法,归并到第 k 个数即可停止。
一般归并排序是两个数组归并,而本题是 n 个数组归并,所以需要用小根堆维护,以优化时间复杂度。
🍁代码:(Java、C++)
法一:二分查找
Java
class Solution {public int kthSmallest(int[][] matrix, int k) {int n = matrix.length;int l = matrix[0][0], h = matrix[n - 1][n - 1];while(l <= h){int mid = l + (h - l) / 2;int cnt = 0;for(int i = 0; i < n; i++){for(int j = 0; j < n && matrix[i][j] <= mid; j++){cnt++;}}if(cnt < k) l = mid + 1;else h = mid - 1;}return l;}
}
C++
class Solution {
public:int kthSmallest(vector<vector<int>>& matrix, int k) {int n = matrix.size();int l = matrix[0][0], h = matrix[n - 1][n - 1];while(l <= h){int mid = l + (h - l) / 2;int cnt = 0;for(int i = 0; i < n; i++){for(int j = 0; j < n && matrix[i][j] <= mid; j++){cnt++;}}if(cnt < k) l = mid + 1;else h = mid - 1;}return l;}
};
法二:归并排序
Java
class Solution {public int kthSmallest(int[][] matrix, int k) {PriorityQueue<int[]> pq = new PriorityQueue<int[]>(new Comparator<int[]>() {public int compare(int[] a, int[] b){return a[0] - b[0];}});int n = matrix.length;for(int i = 0; i < n; i++){//第一列分别为n数组的头结点pq.offer(new int[] {matrix[i][0], i, 0});}for(int i = 0; i < k - 1; i++){int[] now = pq.poll();//弹出最小的那个if(now[2] != n - 1){//不是一行的最后一个元素pq.offer(new int[]{matrix[now[1]][now[2] + 1], now[1], now[2] + 1});}}return pq.poll()[0];}
}
C++
class Solution {
public:int kthSmallest(vector<vector<int>>& matrix, int k) {struct point{int val, x, y;point(int val, int x, int y): val(val), x(x), y(y){};bool operator> (const point& a)const{return this->val > a.val;}};priority_queue<point, vector<point>, greater<point>> que;int n = matrix.size();for(int i = 0; i < n; i++){que.emplace(matrix[i][0], i, 0);}for(int i = 0; i < k - 1; i++){point now = que.top();que.pop();if(now.y != n - 1){que.emplace(matrix[now.x][now.y + 1], now.x, now.y + 1);}}return que.top().val;}
};
🚀 运行结果:

🕔 复杂度分析:
- 时间复杂度: O ( n l o g ( r − l ) ) O(nlog(r - l)) O(nlog(r−l)),二分查找进行次数为 O ( n l o g ( r − l ) ) O(nlog(r - l)) O(nlog(r−l)), 每次操作时间复杂度为 O ( n ) O(n) O(n)。归并排序时间复杂度为 O ( k l o g n ) O(klogn) O(klogn),归并
k次,每次堆中插入和弹出的操作时间复杂度均为 l o g n logn logn。 - 空间复杂度: O ( 1 ) O(1) O(1);归并排序空间复杂度为 O ( n ) O(n) O(n),堆的大小始终为
n。
题目来源:力扣。
放弃一件事很容易,每天能坚持一件事一定很酷,一起每日一题吧!
关注我 leetCode专栏,每日更新!
注: 如有不足,欢迎指正!
相关文章:

( 数组和矩阵) 378. 有序矩阵中第 K 小的元素 ——【Leetcode每日一题】
❓378. 有序矩阵中第 K 小的元素 难度:中等 给你一个 n x n n x n nxn 矩阵 m a t r i x matrix matrix ,其中每行和每列元素均按升序排序,找到矩阵中第 k 小的元素。 请注意,它是 排序后 的第 k 小元素,而不是第 …...
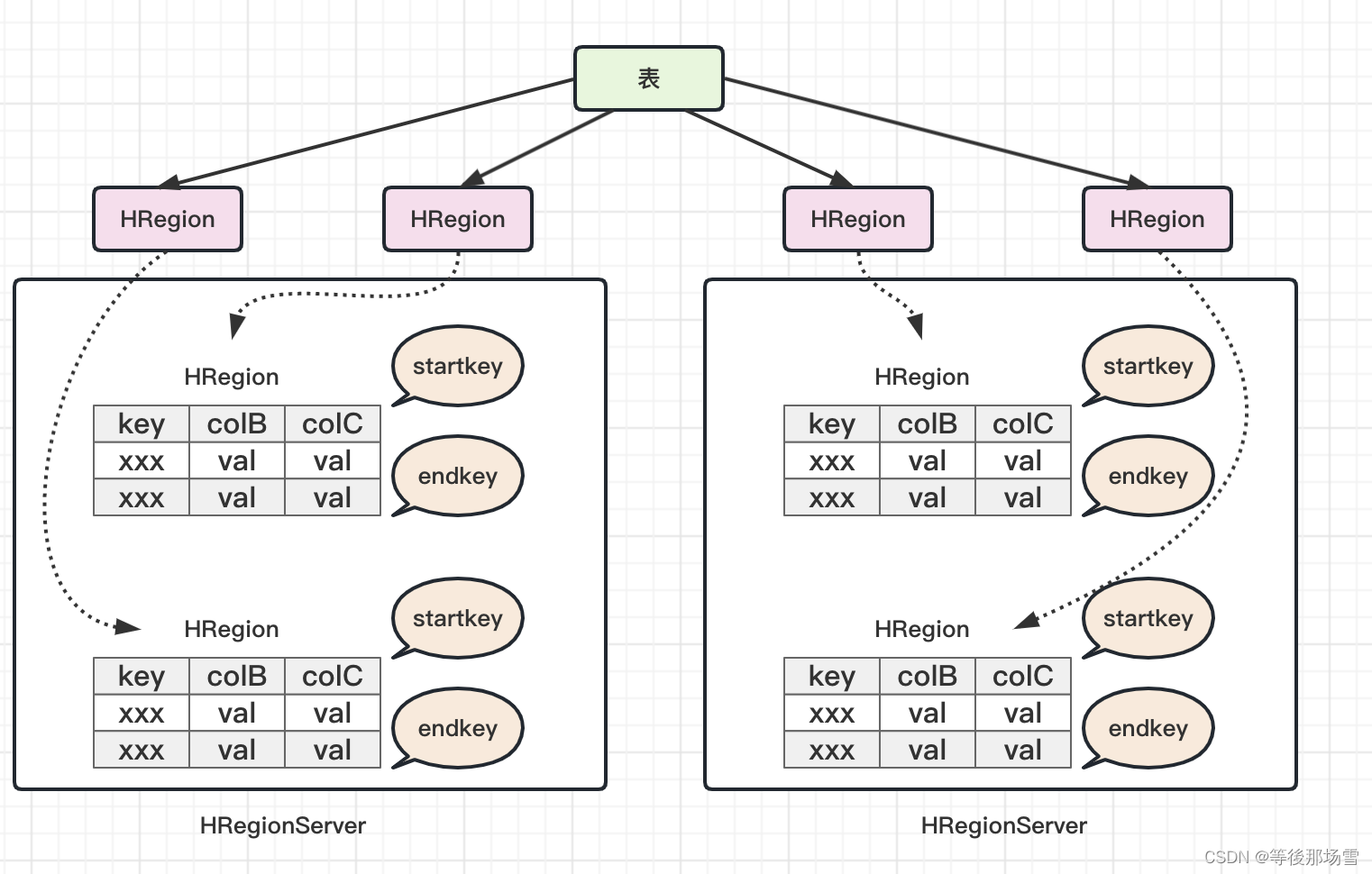
HBase架构篇 - Hadoop家族的天之骄子HBase
HBase的基本组成结构 表(table) HBase 的数据存储在表中。表名是一个字符串。表由行和列组成。 行(row) HBase 的行由行键(rowkey)和 n 个列(column)组成。行键没有数据类型&…...

STL及常用容器vector、list和deque的介绍
vector和built-in数组类似,它拥有一段连续的内存空间,并且起始地址不变,因此它能非常好的支持随机存取,即[]操作符,即可以以数组下标的方式来访问或遍历。但由于它的内存空间是连续的,所以在中间进行插入和删除会造成内存块的拷贝,另外,当该数组后的内存空间不够时,需…...

SpringBoot统一功能处理(统⼀⽤户登录权限验证、统⼀异常处理、统⼀数据格式封装)
统⼀⽤户登录权限验证 1、最初的用户登录效验:在每个方法里面获取session和 session 中的用户信息,如果存在用户,那么就认为登录成功了,否则就登录失败了。 2、第二版用户登录效验:提供了统一的方法,在每个需要验证的方法中调用…...
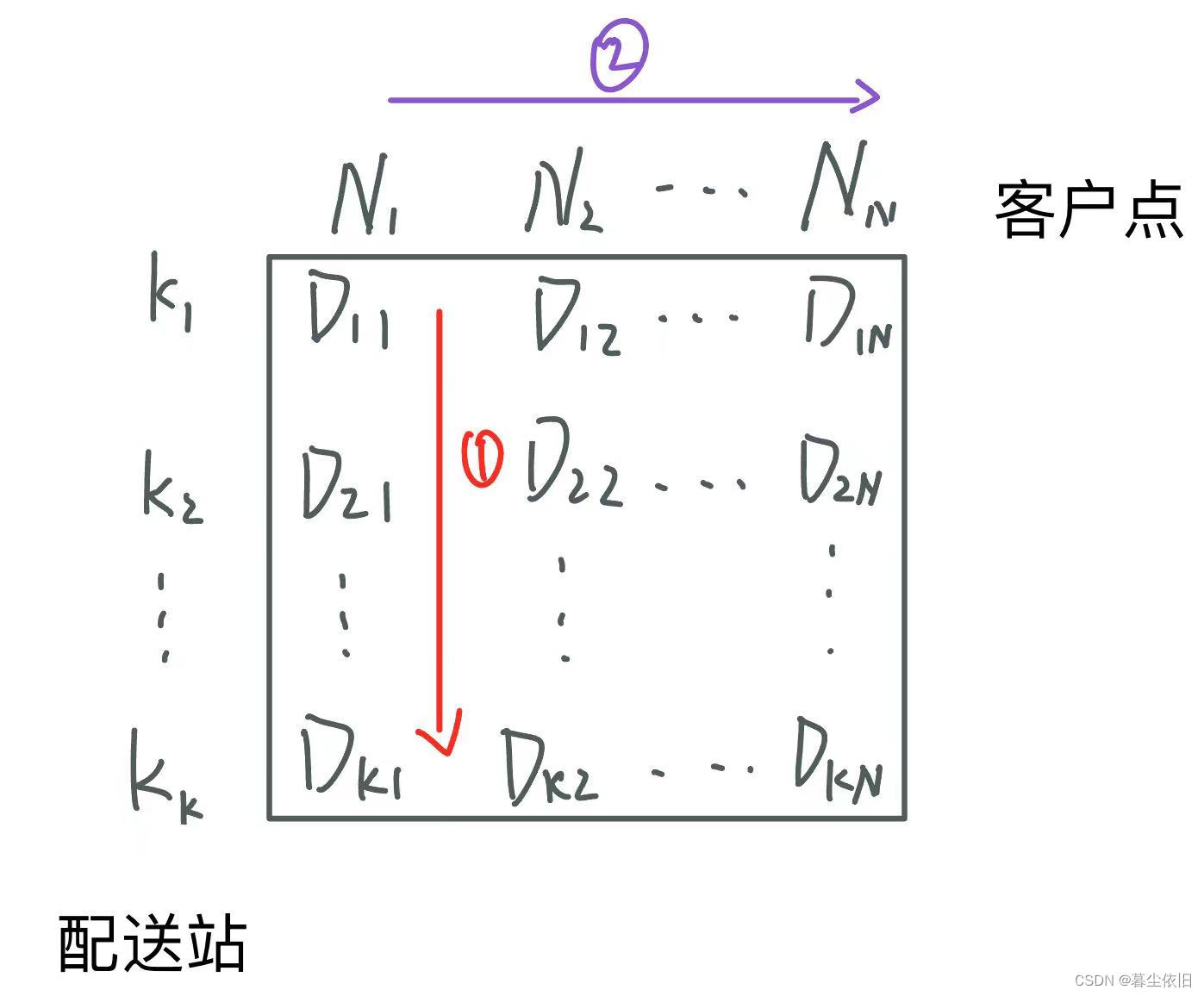
华为实习笔试复盘(1)配送站和客户问题
写在前面 自己玩了很多项目,但是最近准备秋招的过程中,发现自己对于算法和编程语言的基本功夫实在是太欠缺了。 投递了华为的实习岗位,4.26参加机考,一做题就发现了自己很多地方都不会。这里写下笔试后的复盘以警醒自己。 题目 …...

alibaba yalantingLibs struct_pack代码梳理
这里写目录标题 struct_pack 接口序列化序列化对象到新字节容器序列化对象到容器尾部将序列化结果保存到指针指向的内存中多参数序列化将序列化结果保存到输出流自定义类型序列化序列化到自定义的输出流 反序列化基本反序列化从指针指向的内存中反序列化反序列化到已有对象多参…...
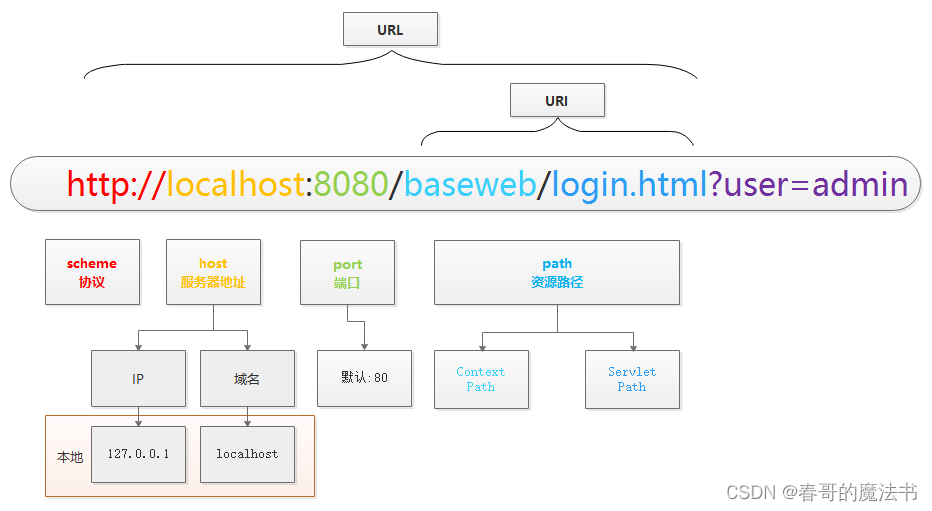
JavaWeb( 二 ) URL
1.4.URL统一资源定位符 URL代表Uniform Resource Locator 统一资源定位符,也叫 URL地址 。是用于标识和定位Web上资源的地址,通常用于在Web浏览器中访问网站和文件。 URL由若干部分组成,scheme:// host : port / path 例如: htt…...

Python斐波那契数列
斐波那契数列是一个经典的数学问题,在 Python 中可以使用多种方法来实现,下面是几个常见的实现方式: 1. 使用递归 python def fibonacci_recursive(n): if n < 1: return n else: return fibonacci_recursive(n…...
)
华为OD机试 - 模拟商场优惠打折(Python)
题目描述 模拟商场优惠打折,有三种优惠券可以用,满减券、打折券和无门槛券。 满减券:满100减10,满200减20,满300减30,满400减40,以此类推不限制使用; 打折券:固定折扣92折,且打折之后向下取整,每次购物只能用1次; 无门槛券:一张券减5元,没有使用限制。 每个人…...
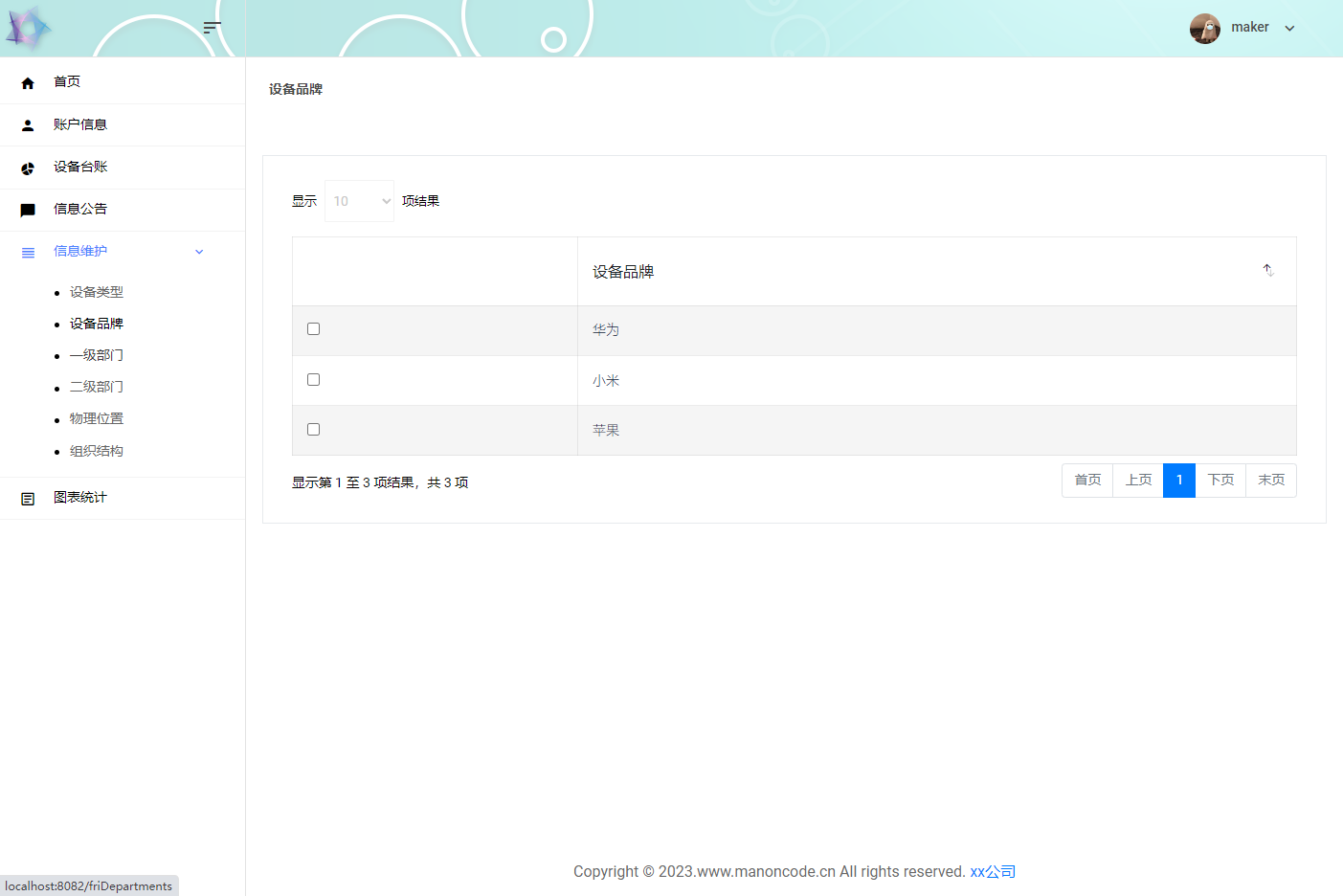
【JAVA程序设计】(C00132)基于SSM的固定资产管理系统
基于SSM的固定资产管理系统 项目简介项目获取开发环境项目技术运行截图 项目简介 本系统为基于SSM的固定资产管理系统,本系统分为二种用户:超级管理员和普通管理员; 超级管理员功能: 首页查看、设备管理、平台账户管理、设备台账…...

简单的无理函数的不定积分
前置知识: 直接积分法有理函数的不定积分 简单的无理函数的不定积分 对无理函数积分的基本方法就是通过换元将其化为有理函数的积分。下面讲讲几类无理函数积分的求法。 注: R ( u , v ) R(u,v) R(u,v)是由 u , v u,v u,v与常数经过有限次四则运算得…...

《国际联网安全保护管理办法》
1.基本信息 (1997年12月11日国务院批准 1997年12月16日公安部令第33号发布 根据2011年1月8日《国务院关于废止和修改部分行政法规的决定》修订) 2.办法内容 第一章 总 则 第一条为了加强对计算机信息网络国际联网的安全保护,维护公共…...

Redis常用命令
目录 一. 字符串string常用操作命令 二. 哈希hash常用操作命令 三. 列表list常用操作命令 四. 集合set常用操作命令 五. 有序集合sorted set常用操作命令 六. 通用命令 一. 字符串string常用操作命令 SET key value 设置指定key的值GET key 获取指定key的值 SETEX key…...

功能齐全的 DIY ESP32 智能手表设计之原理图讲解二
相关设计资料下载ESP32 智能手表带心率、指南针设计资料(包含Arduino源码+原理图+Gerber+3D文件).zip 目录 构建 ESP32 智能手表所需的组件 光照度传感器电路讲解...

烦恼的高考志愿
烦恼的高考志愿 题目背景 计算机竞赛小组的神牛 V 神终于结束了高考,然而作为班长的他还不能闲下来,班主任老 t 给了他一个艰巨的任务:帮同学找出最合理的大学填报方案。可是 v 神太忙了,身后还有一群小姑娘等着和他约会&#x…...

【地铁上的设计模式】--结构型模式:适配器模式
前面几篇文章我们学习了创建型模式,从本篇文章开始,我们将学习结构型模式。 什么是结构型模式 结构型模式是一种设计模式,它描述了如何将类或对象结合在一起形成更大的结构,以提供新的功能或实现更复杂的行为。结构型模式包括以…...
重大剧透:你不用ChatGPT,它砸你饭碗
早晨看到路透社报道,盖茨说,与其争论技术的未来,不如专注于如何更好地利用人工智能。 这可能是他对马斯克他们呼吁暂停AI研发6个月的一种回应吧。 有种古语说:天下大势,浩浩汤汤,顺之者昌,逆之者…...

状态机模式
状态模式 状态模式定义:使用场景角色定义1. State一抽象状态角色2. ConcreteState一-具体状态角色3. Context--环境角色 需求背景1. 订单状态抽象类2. 定义订单具体状态类并集成基类(抽象类)2.1 订单创建状态2.2 订单已支付状态2.3 订单已发货状态2.4 订…...
瑞吉外卖:后台系统登录功能
文章目录 需求分析代码开发创建实体类导入返回结果类Rcontroller、service与mapperlogin.html 需求分析 点击登录按钮后,浏览器以POST方式向employee/login提交username和password,服务器经过处理后向浏览器返回某种格式的数据,其中包含&…...
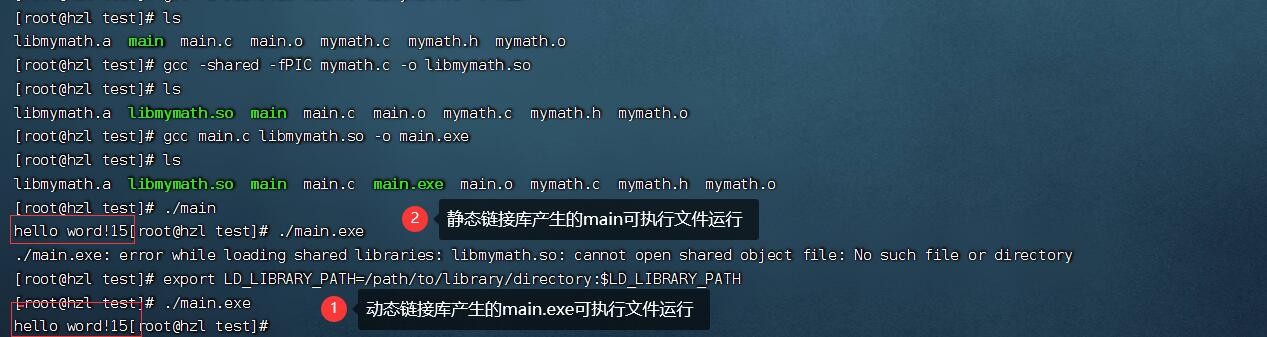
Linux拓展:链接库
一.说明 本篇博客介绍Linux操作系统下的链接库相关知识,由于相关概念已在Windows下链接库一文中介绍,本篇博客直接上操作。 二.静态链接库的创建和使用 1.提前看 这里主要介绍的是C语言的链接库技术,而在Linux下实现C语言程序,…...

XML Group端口详解
在XML数据映射过程中,经常需要对数据进行分组聚合操作。例如,当处理包含多个物料明细的XML文件时,可能需要将相同物料号的明细归为一组,或对相同物料号的数量进行求和计算。传统实现方式通常需要编写脚本代码,增加了开…...

C++_核心编程_多态案例二-制作饮品
#include <iostream> #include <string> using namespace std;/*制作饮品的大致流程为:煮水 - 冲泡 - 倒入杯中 - 加入辅料 利用多态技术实现本案例,提供抽象制作饮品基类,提供子类制作咖啡和茶叶*//*基类*/ class AbstractDr…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(二)
HoST框架核心实现方法详解 - 论文深度解读(第二部分) 《Learning Humanoid Standing-up Control across Diverse Postures》 系列文章: 论文深度解读 + 算法与代码分析(二) 作者机构: 上海AI Lab, 上海交通大学, 香港大学, 浙江大学, 香港中文大学 论文主题: 人形机器人…...

python/java环境配置
环境变量放一起 python: 1.首先下载Python Python下载地址:Download Python | Python.org downloads ---windows -- 64 2.安装Python 下面两个,然后自定义,全选 可以把前4个选上 3.环境配置 1)搜高级系统设置 2…...

理解 MCP 工作流:使用 Ollama 和 LangChain 构建本地 MCP 客户端
🌟 什么是 MCP? 模型控制协议 (MCP) 是一种创新的协议,旨在无缝连接 AI 模型与应用程序。 MCP 是一个开源协议,它标准化了我们的 LLM 应用程序连接所需工具和数据源并与之协作的方式。 可以把它想象成你的 AI 模型 和想要使用它…...

【项目实战】通过多模态+LangGraph实现PPT生成助手
PPT自动生成系统 基于LangGraph的PPT自动生成系统,可以将Markdown文档自动转换为PPT演示文稿。 功能特点 Markdown解析:自动解析Markdown文档结构PPT模板分析:分析PPT模板的布局和风格智能布局决策:匹配内容与合适的PPT布局自动…...

select、poll、epoll 与 Reactor 模式
在高并发网络编程领域,高效处理大量连接和 I/O 事件是系统性能的关键。select、poll、epoll 作为 I/O 多路复用技术的代表,以及基于它们实现的 Reactor 模式,为开发者提供了强大的工具。本文将深入探讨这些技术的底层原理、优缺点。 一、I…...

laravel8+vue3.0+element-plus搭建方法
创建 laravel8 项目 composer create-project --prefer-dist laravel/laravel laravel8 8.* 安装 laravel/ui composer require laravel/ui 修改 package.json 文件 "devDependencies": {"vue/compiler-sfc": "^3.0.7","axios": …...

视频行为标注工具BehaviLabel(源码+使用介绍+Windows.Exe版本)
前言: 最近在做行为检测相关的模型,用的是时空图卷积网络(STGCN),但原有kinetic-400数据集数据质量较低,需要进行细粒度的标注,同时粗略搜了下已有开源工具基本都集中于图像分割这块,…...

排序算法总结(C++)
目录 一、稳定性二、排序算法选择、冒泡、插入排序归并排序随机快速排序堆排序基数排序计数排序 三、总结 一、稳定性 排序算法的稳定性是指:同样大小的样本 **(同样大小的数据)**在排序之后不会改变原始的相对次序。 稳定性对基础类型对象…...
