Latex 定理和证明类环境(amsthm)和(ntheorm)的区别
最近在写毕业论文,出现了一些定理和证明的环境的问题,问题出现在对两个包的理解程度不够的问题上:
\RequirePackage{ntheorem}
1、\newtheorem*{proof}{\hspace{2em}证:} 这个是让证明失去计数原则,该命令不能用于 amsthm
2、该证明环境下,定理的字体和证明的字体一致。
3、关键:证明的环境中,所有的引用(\ref{})都会斜体出现。相对来说比较丑。可通过增加公式符号解决:$\ref{--}$ 。
4、证明结束不会有 证明结束的标志。
\RequirePackage{amsthm}
参考1:Latex 定理和证明类环境的配置(amsthm) - 知乎 (zhihu.com)
参考2: LaTeX (7)——amsthm - 知乎 (zhihu.com):
1、该包是自动添加 qed symbol。即证明自动结束的标志。
2、证明proof 环境不参与自动编号,与包ntheorem的区别。
参考: LaTeX系列笔记(10)-证明 - 知乎 (zhihu.com)
可通下命令修改证明的两字的字体和证毕的标志。
\renewcommand{\proofname}{\indent\bf 证明:} %修改证明字体
\renewcommand{\qedsymbol}{证毕} %设置QED为其它形式
\renewcommand{\qedsymbol}{$\blacksquare$} % 证毕符号改成黑色的正方形
3、该包有个问题就是定理后面会附上一个点,比如 定理2.1.
latex排版的一个问题,怎么去掉1后面的点? - 知乎 (zhihu.com)
\newtheoremstyle{mystyle}
{}
{}
{}
{} %定理缩进两格
{\bfseries}
{} %定理编号后无点
{.5em}
{}
使用自定义的环境要是先声明比如:
\theoremstyle{mystyle}
\newtheorem{definition}{\hspace{2em}定义}[chapter]
\newtheorem{proposition}{\hspace{2em}命题}[chapter]
\newtheorem{property}{\hspace{2em}性质}[chapter]
\newtheorem{lemma}{\hspace{2em}引理}[chapter]
\newtheorem{theorem}{\hspace{2em}定理}[chapter]
\newtheorem{corollary}{\hspace{2em}推论}[chapter]
\newtheorem{example}{\hspace{2em}例}
\newtheorem{remark}{\hspace{2em}注}
\renewcommand{\proofname}{\indent\bf 证明:}
\renewcommand{\qedsymbol}{$\blacksquare$} % 证毕符号改成黑色的正方形
这里给出一个不推荐 ntheorem的理由:
转载:为什么推荐使用定理宏包thmtools? - 知乎 (zhihu.com)
ntheorem的劣势:有一些长期存在而未修复的 bug,缺乏维护。相关讨论和问答(不全),见- Theorem packages: which to use, which conflict?
这是 2010 年写的三个定理宏包的比较,其中提到的ntheorem的 bug,现在仍然存在 - ntheorem with thmmarks and standard options fails when thebibliography is empty
这是 2020 年 5 月的问答,涉及ntheorem的一个具体 bug。- 回答该问题的是 TeX-SX 上积分最高的用户、LaTeX3 团队(他们维护着 LaTeX2e)成员之一的 egreg,
- 他在评论里回应为什么不推荐使用
ntheorem时说,"unfortunately,ntheoremseems essentially unmaintaned and has severe problems."
- Theorem packages: which to use, which conflict?
amsmath和thmtools的优势:前者实现和功能都简单而稳定,后者提供了 key-value 接口,功能也更丰富。
相关文章:
和(ntheorm)的区别)
Latex 定理和证明类环境(amsthm)和(ntheorm)的区别
最近在写毕业论文,出现了一些定理和证明的环境的问题,问题出现在对两个包的理解程度不够的问题上: \RequirePackage{ntheorem} 1、\newtheorem*{proof}{\hspace{2em}证:} 这个是让证明失去计数原则,该命令不能用于 amsthm 2…...

Yolov8改进---注意力全家桶,小目标涨点
💡💡💡💡💡💡💡💡💡💡注意力全家桶💡💡💡💡💡💡💡💡💡💡💡 基于Yolov8的注意力机制研究,提升小目标、遮挡物、难样本等检测性能...

[Linux]网络连接、资源共享
⭐作者介绍:大二本科网络工程专业在读,持续学习Java,输出优质文章 ⭐作者主页:逐梦苍穹 ⭐所属专栏:Linux基础操作。本文主要是分享一些Linux系统常用操作,内容主要来源是学校作业,分享出来的…...

来上海一个月的记录、思考和感悟
作者 | gongyouliu 编辑 | gongyouliu 从4月3号早上来上海,到今天差不多整整一个月了,也是自己正式从杭州离职创业(我更愿意称之为自由职业者,毕竟我没有招聘全职员工,有两个朋友业余时间在帮我)的第一个月…...
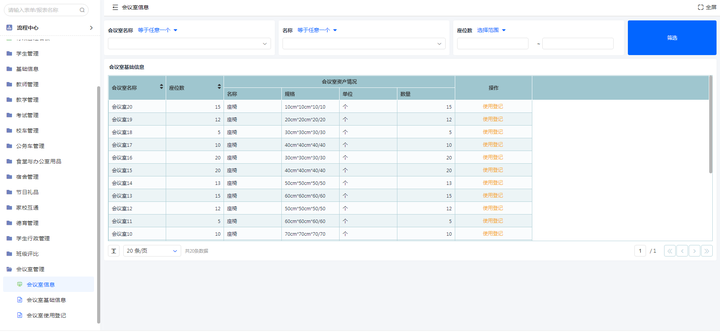
学校信息化管理系统通常包含哪些功能?
学校管理信息化是现代教育发展的必然趋势,随着信息技术的飞速发展,学校管理也逐渐地实现了信息化。信息化的学校管理已经成为教育现代化建设的重要内容,也是提高学校教育教学质量和保障学生安全的重要手段。 作为一款低代码开发平台…...
 -- Calendar()(日历类))
Java时间类(三) -- Calendar()(日历类)
java.util.Calendar类是一个抽象类,它提供了日期计算的相关功能、获取或设置各种日历字段的方法。 protected Calendar() 构造方法为protected修饰,无法直接创建该对象。1. Calendar()的常用方法: 方法名说明static Calendar getInstance()使用默认时区和区域获取日历vo…...

【五一创作】QML、Qt Quick /Qt中绘制圆形
目录标题 Qt Quick中绘制圆形扩展知识Canvas 模块介绍Shapes 模块介绍 Qt Widgets 中绘制圆形两种方式的比较 Qt Quick中绘制圆形 有多种方法可以在 Qt Quick 中绘制圆形。以下是一些主要方法: 使用 Canvas 元素 使用 Shapes 模块: a. 使用 PathArc 和…...

【软考数据库】第七章 关系数据库
目录 7.1 关系数据库概述 7.2 关系代数 7.3 元组演算与域演算 7.4 查询优化 7.5 关系数据库设计 7.6 模式分解 前言: 笔记来自《文老师软考数据库》教材精讲,精讲视频在b站,某宝都可以找到,个人感觉通俗易懂。 7.1 关系数据…...

《SpringBoot中间件设计与实战》第1章 什么是中间件
一、写在前面 在互联网应用初期,所有用于支撑系统建设的,框架结构、基础工具、业务逻辑、功能服务包括页面展示等,都是在一个系统中开发完成,最终也只是把系统和数据库部署在同一台服务器上。也就是大多数开发者入门所接触到的 “单体” 系统。 那为什么会有中间件这个玩…...
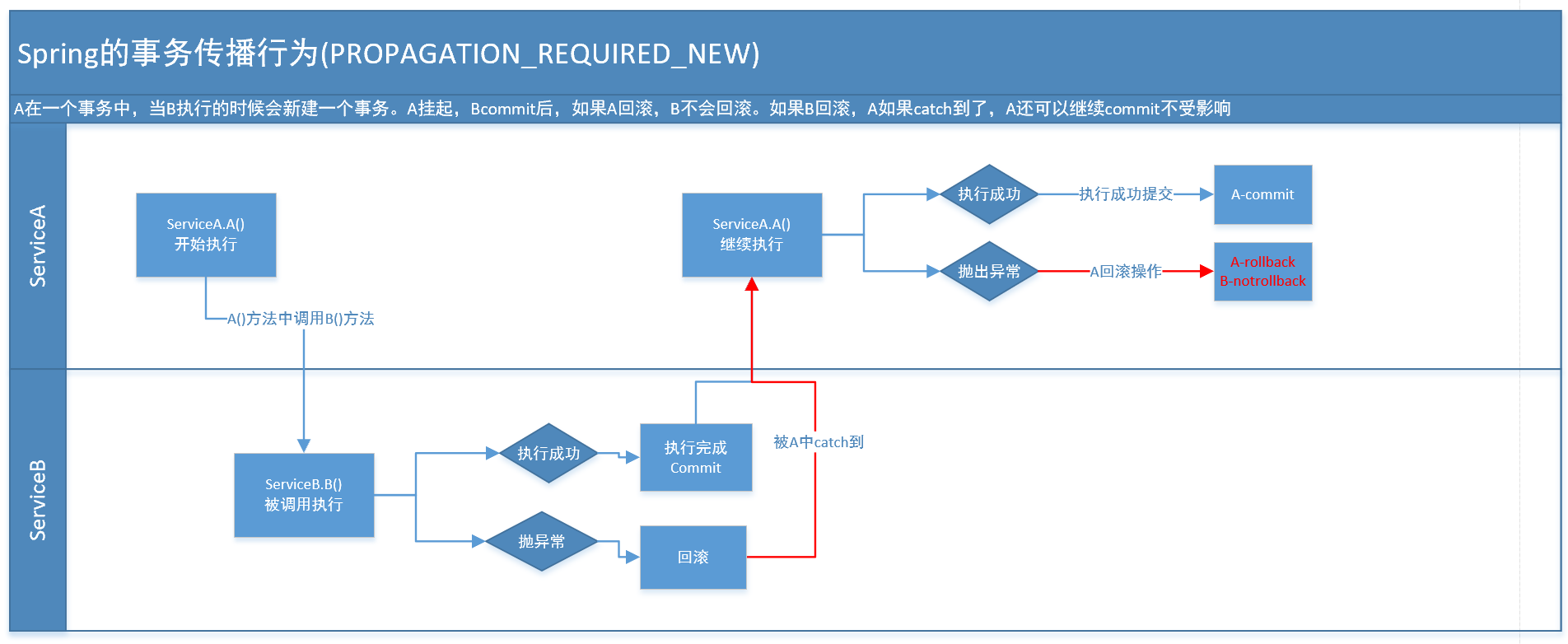
spring常用的事务传播行为
事务传播行为介绍 Spring中的7个事务传播行为: 事务行为 说明 PROPAGATION_REQUIRED 支持当前事务,假设当前没有事务。就新建一个事务 PROPAGATION_SUPPORTS 支持当前事务,假设当前没有事务,就以非事务方式运行 PROPAGATION_MANDATORY…...
【Python】什么是爬虫,爬虫实例
有s表示加密的访问方式 一、初识爬虫 什么是爬虫 网络爬虫,是一种按照一定规则,自动抓取互联网信息的程序或者脚本。由于互联网数据的多样性和资源的有限性,根据用户需求定向抓取相关网页并分析已成为如今主流的爬取策略爬虫可以做什么 你可以…...
)
JavaScript学习笔记(三)
文章目录 第7章:迭代器与生成器1. 迭代器模式2. 生成器 第8章:对象、类与面向对象编程1. 理解对象2. 创建对象3. 继承:依靠原型链实现4. 类class 第10章:函数1. 函数定义的方式有:函数声明、函数表达式、箭头函数&…...
文鼎创智能物联云原生容器化平台实践
作者:sekfung,深圳市文鼎创数据科技有限公司研发工程师,负责公司物联网终端平台的开发,稳定性建设,容器化上云工作,擅长使用 GO、Java 开发分布式系统,持续关注分布式,云原生等前沿技…...

深入了解SpringMVC框架,探究其优缺点、作用以及使用方法
一、什么是Spring MVC SpringMVC是一种基于Java的Web框架,与Spring框架紧密结合,用于开发具备WebApp特性的Java应用程序。Spring MVC是Spring Framework的一部分,因此它具有与Spring框架相同的特性和理念。 二、SpringMVC的优缺点 1. 优点…...
Git教程(一)
1、Git概述 1.1 、Git历史 同生活中的许多伟大事件一样,Git 诞生于一个极富纷争大举创新的年代。Linux 内核开源项目有着为数众广的参与者。绝大多数的 Linux 内核维护工作都花在了提交补丁和保存归档的繁琐事务上(1991-2002年间)…...
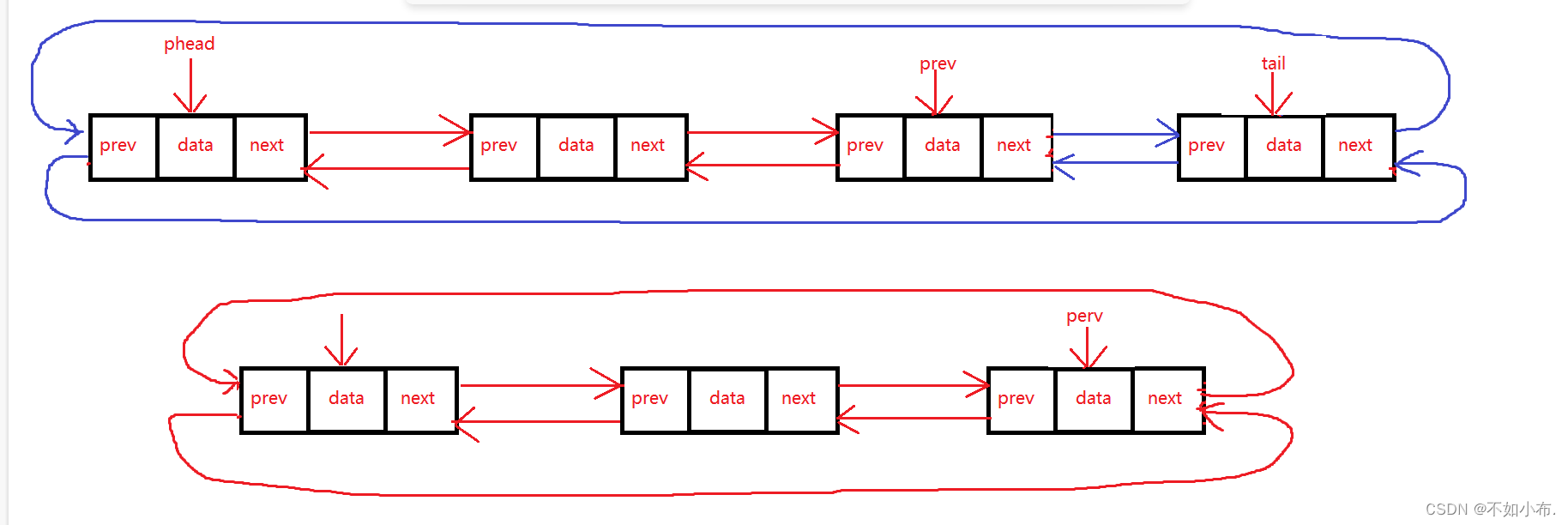
数据结构篇三:双向循环链表
文章目录 前言双向链表的结构功能的解析及实现1. 双向链表的创建2. 创建头节点(初始化)3. 创建新结点4. 尾插5. 尾删6. 头插7. 头删8. 查找9. 在pos位置前插入10. 删除pos位置的结点11. 销毁 代码实现1.ListNode.h2. ListNode.c3. test.c 总结 前言 前面…...
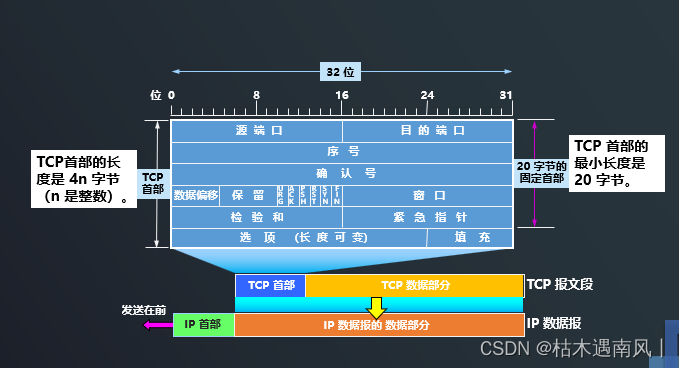
day10 TCP是如何实现可靠传输的
TCP最主要的特点 1、TCP是面向连接的运输层协议。( 每一条TCP连接只能有两个端点(endpoint),每一条TCP连接只能是点对点的(一对一)) 2、TCP提供可靠交付的服务。 3、TCP提供全双工通信。 4…...

Python | 人脸识别系统 — 背景模糊
本博客为人脸识别系统的背景模糊代码解释 人脸识别系统博客汇总:人脸识别系统-博客索引 项目GitHub地址:Su-Face-Recognition: A face recognition for user logining 注意:阅读本博客前请先参考以下博客 工具安装、环境配置:人脸…...

YOLOv5+单目测量物体尺寸(python)
YOLOv5单目测量尺寸(python) 1. 相关配置2. 测距原理3. 相机标定3.1:标定方法1(针对图片)3.2:标定方法2(针对视频) 4. 相机测距4.1 测距添加4.2 细节修改(可忽略…...

C++异常
C异常 提到异常,大家一定不陌生,在学习new关键字的时候就提到了开空间失败会导致抛异常。其实异常在我们生活中的使用是很多的,有些时候程序发生错误以后我们并不希望程序就直接退出,针对不同的情况,我们更希望有不同的…...

Cursor实现用excel数据填充word模版的方法
cursor主页:https://www.cursor.com/ 任务目标:把excel格式的数据里的单元格,按照某一个固定模版填充到word中 文章目录 注意事项逐步生成程序1. 确定格式2. 调试程序 注意事项 直接给一个excel文件和最终呈现的word文件的示例,…...

K8S认证|CKS题库+答案| 11. AppArmor
目录 11. AppArmor 免费获取并激活 CKA_v1.31_模拟系统 题目 开始操作: 1)、切换集群 2)、切换节点 3)、切换到 apparmor 的目录 4)、执行 apparmor 策略模块 5)、修改 pod 文件 6)、…...

【HarmonyOS 5.0】DevEco Testing:鸿蒙应用质量保障的终极武器
——全方位测试解决方案与代码实战 一、工具定位与核心能力 DevEco Testing是HarmonyOS官方推出的一体化测试平台,覆盖应用全生命周期测试需求,主要提供五大核心能力: 测试类型检测目标关键指标功能体验基…...

【解密LSTM、GRU如何解决传统RNN梯度消失问题】
解密LSTM与GRU:如何让RNN变得更聪明? 在深度学习的世界里,循环神经网络(RNN)以其卓越的序列数据处理能力广泛应用于自然语言处理、时间序列预测等领域。然而,传统RNN存在的一个严重问题——梯度消失&#…...

全球首个30米分辨率湿地数据集(2000—2022)
数据简介 今天我们分享的数据是全球30米分辨率湿地数据集,包含8种湿地亚类,该数据以0.5X0.5的瓦片存储,我们整理了所有属于中国的瓦片名称与其对应省份,方便大家研究使用。 该数据集作为全球首个30米分辨率、覆盖2000–2022年时间…...

微信小程序 - 手机震动
一、界面 <button type"primary" bindtap"shortVibrate">短震动</button> <button type"primary" bindtap"longVibrate">长震动</button> 二、js逻辑代码 注:文档 https://developers.weixin.qq…...

【android bluetooth 框架分析 04】【bt-framework 层详解 1】【BluetoothProperties介绍】
1. BluetoothProperties介绍 libsysprop/srcs/android/sysprop/BluetoothProperties.sysprop BluetoothProperties.sysprop 是 Android AOSP 中的一种 系统属性定义文件(System Property Definition File),用于声明和管理 Bluetooth 模块相…...

ServerTrust 并非唯一
NSURLAuthenticationMethodServerTrust 只是 authenticationMethod 的冰山一角 要理解 NSURLAuthenticationMethodServerTrust, 首先要明白它只是 authenticationMethod 的选项之一, 并非唯一 1 先厘清概念 点说明authenticationMethodURLAuthenticationChallenge.protectionS…...

图表类系列各种样式PPT模版分享
图标图表系列PPT模版,柱状图PPT模版,线状图PPT模版,折线图PPT模版,饼状图PPT模版,雷达图PPT模版,树状图PPT模版 图表类系列各种样式PPT模版分享:图表系列PPT模板https://pan.quark.cn/s/20d40aa…...

Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决
Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决 问题背景 在一个基于 Spring Cloud Gateway WebFlux 构建的微服务项目中,新增了一个本地验证码接口 /code,使用函数式路由(RouterFunction)和 Hutool 的 Circle…...
