Leetcode326. 3 的幂
Every day a leetcode
题目来源:326. 3 的幂
相似题目:342. 4的幂
解法1:递归
代码:
/** @lc app=leetcode.cn id=326 lang=cpp** [326] 3 的幂*/// @lc code=start
class Solution
{
public:bool isPowerOfThree(int n){if (n <= 0)return false;if (n == 1)return true;if (n % 3 == 0)return isPowerOfThree(n / 3);elsereturn false;}
};
// @lc code=end结果:
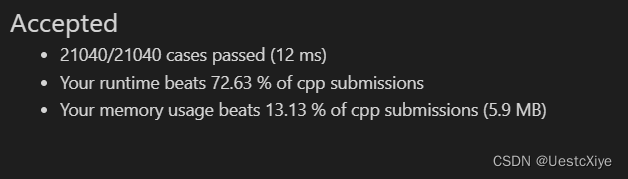
复杂度分析:
时间复杂度:O(logn),当n是3的幂时,需要除以3的次数为log3n=O(logn);当n 不是3的幂时,需要除以3的次数小于该值。
空间复杂度:O(logn),取决于递归栈的具体实现。
解法2:暴力
在题目给定的32位有符号整数的范围内,最小的3的幂为30=1,最大的3的幂为319=1162261467。
我们使用数组记录30到319,再在这个数组里查找即可。
代码:
/** @lc app=leetcode.cn id=326 lang=cpp** [326] 3 的幂*/// @lc code=start
// class Solution
// {
// public:
// bool isPowerOfThree(int n)
// {
// if (n <= 0)
// return false;
// if (n == 1)
// return true;
// if (n % 3 == 0)
// return isPowerOfThree(n / 3);
// else
// return false;
// }
// };class Solution
{
public:bool isPowerOfThree(int n){vector<int> nums;for (int i = 0; i <= 19; i++)nums.push_back(pow(3, i));return count(nums.begin(), nums.end(), n);}
};
// @lc code=end结果:
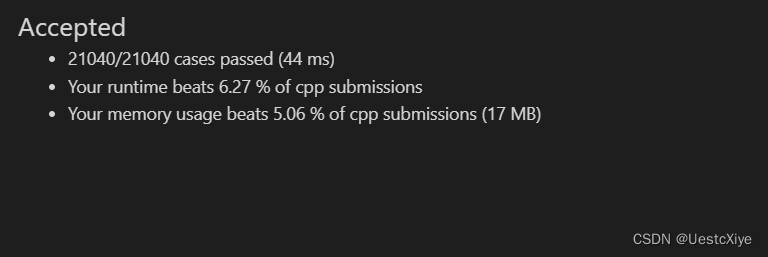
复杂度分析:
时间复杂度:O(1)。
空间复杂度:O(1)。
相关文章:

Leetcode326. 3 的幂
Every day a leetcode 题目来源:326. 3 的幂 相似题目:342. 4的幂 解法1:递归 代码: /** lc appleetcode.cn id326 langcpp** [326] 3 的幂*/// lc codestart class Solution { public:bool isPowerOfThree(int n){if (n <…...

【运动规划算法项目实战】如何在栅格地图中实现Dijkstra算法
文章目录 简介一、算法介绍1.1 Dijkstra算法流程1.2 Dijkstra算法伪代码二、代码实现2.1 ROS实现2.2 RVIZ演示三、总结简介 Dijkstra算法是一种用于图中单源最短路径的贪心算法。在计算机科学和网络设计中广泛应用。该算法从起点开始,通过优先选择距离起点最近的未标记节点来…...
【算法】一文彻底搞懂ZAB算法
文章目录 什么是ZAB 算法?深入ZAB算法1. 消息广播两阶段提交ZAB消息广播过程 2. 崩溃恢复选举参数选举流程 ZAB算法需要解决的两大问题1. 已经被处理的消息不能丢2. 被丢弃的消息不能再次出现 最近需要设计一个分布式系统,需要一个中间件来存储共享的信息…...
【软考高级】2022年系统分析师综合知识
1.( )是从系统的应用领域而不是从系统用户的特定需要中得出的,它们可以是新的功能性需求,或者是对已有功能性需求的约束,或者是陈述特定的计算必须遵守的要求。 A.功能性需求 B. 用户需求 C.产品需求 D.领域需求 2.对于安全关键系…...

关于AI未来的思考和应用场景
关于AI未来的思考和应用场景 AI(人工智能)是当今最热门的技术领域之一,它已经在多个领域产生了深远的影响,如医疗、金融、制造业等。未来,AI将继续发展,并在更多领域产生重要的影响。 AI的未来发展方向有…...
智慧城市规划数字化管理:数字孪生技术的创新应用
随着智能城市的不断发展,数字孪生技术也开始在智慧城市的建设中得到了广泛应用。数字孪生作为一种数字化的复制技术,它可以模拟真实世界中的实体和过程。 在城市规划方面,数字孪生可以帮助城市规划师更加直观地了解城市的整体规划和发展趋势&…...

开心档之C++ 指针
C 指针 学习 C 的指针既简单又有趣。通过指针,可以简化一些 C 编程任务的执行,还有一些任务,如动态内存分配,没有指针是无法执行的。所以,想要成为一名优秀的 C 程序员,学习指针是很有必要的。 正如您所知…...
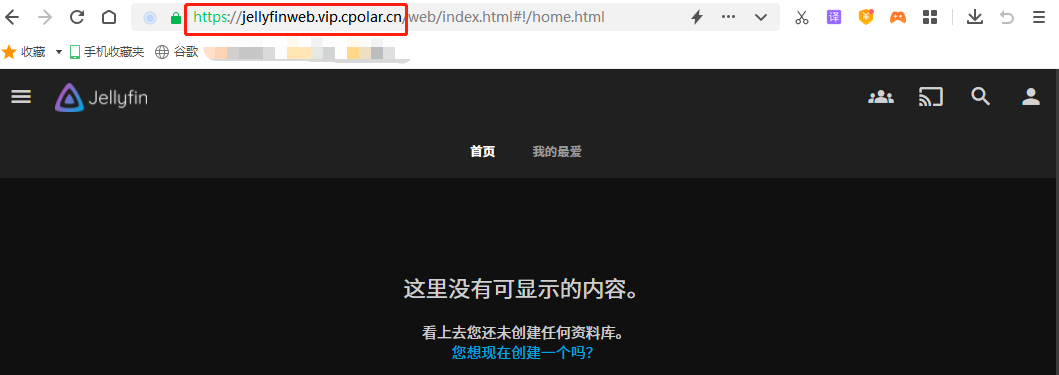
零基础搭建私人影音媒体平台【远程访问Jellyfin播放器】
文章目录 1. 前言2. Jellyfin服务网站搭建2.1. Jellyfin下载和安装2.2. Jellyfin网页测试 3.本地网页发布3.1 cpolar的安装和注册3.2 Cpolar云端设置3.3 Cpolar本地设置 4.公网访问测试5. 结语 转载自内网穿透工具的文章:零基础搭建私人影音媒体平台【远程访问Jelly…...

Abstract Expressionist
古董地图画集 10大最有名的抽象艺术家 抽象表现主义是现代许多不同艺术思想和表达流派中最奇特的艺术运动之一。这场运动开始从社会变革中涌现出来,恰逢第二次世界大战的最后几周和几个月。 这一次,来自世界各地的人们开始欢迎在经历了多年有史以来最致…...
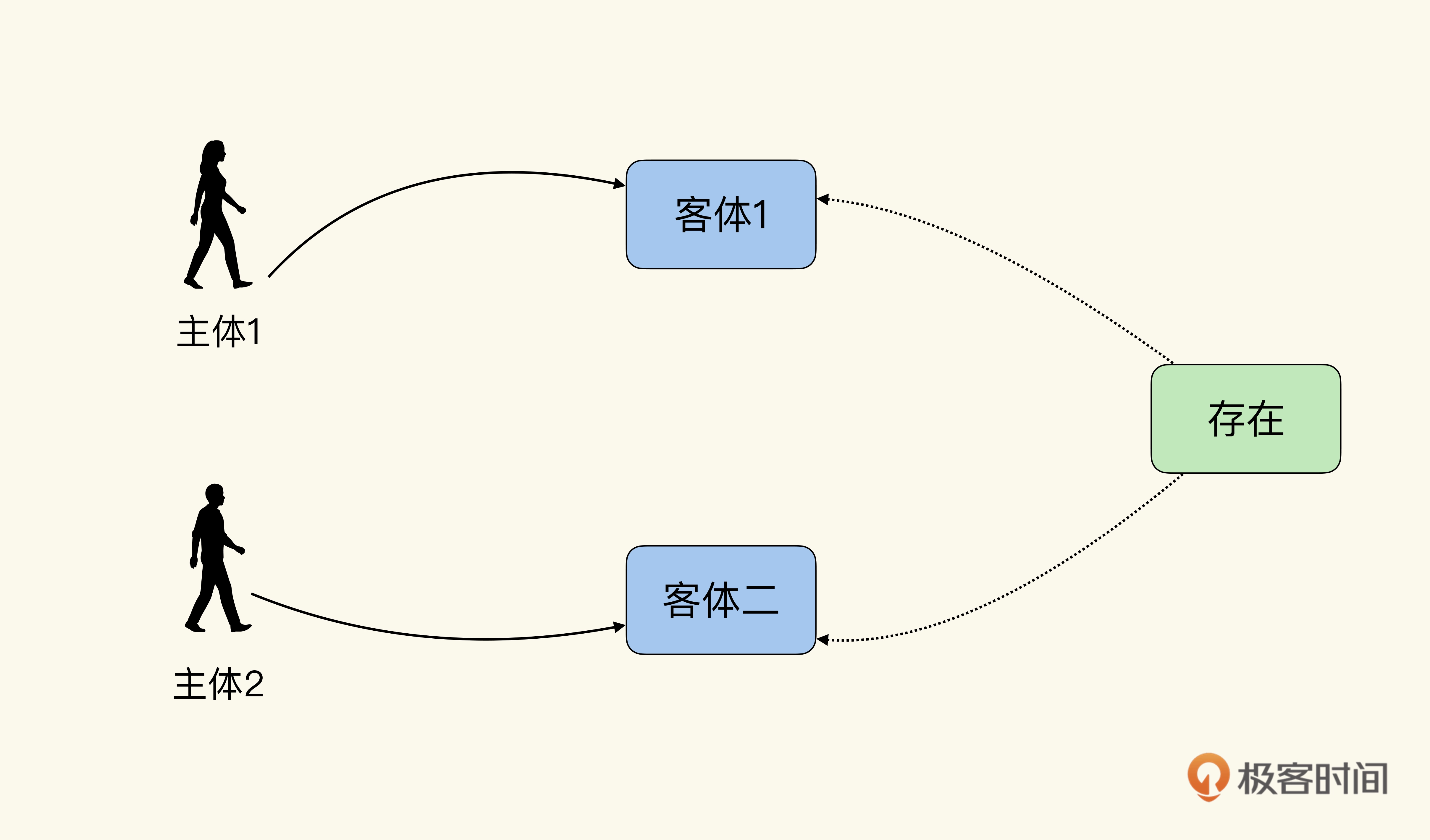
【郭东白架构课 模块二:创造价值】24|节点四:如何减少语义上的分歧?
你好,我是郭东白。上节课我们通过一个篇幅比较长的电商案例,详细展示了为什么在架构活动中会出现语义分歧。同时也描述了,架构师在统一语义这个环节中所要创造的真正价值是什么。即,看到不同角色之间语境的差异,然后通…...

windows下免费本地部署类ChatGpt的国产ChatGLM-6B
ChatGLM-6B 是一个开源的、支持中英双语的对话语言模型,基于 General Language Model (GLM) 架构,具有 62 亿参数。结合模型量化技术,用户可以在消费级的显卡上进行本地部署(INT4 量化级别下最低只需 6GB 显存)。 Chat…...

flask+opencv+实时滤镜(原图、黑白、怀旧、素描)
简介:滤镜,主要是用来实现图像的各种特殊效果。图像滤镜用于改变图像的视觉效果,使其具有特定的风格。下面是这三种滤镜的详细说明: 1、黑白(Grayscale):黑白滤镜将彩色图像转换为灰度图像&…...
计算机算法类SCI,数据库稳定检索19年)
【SCI征稿】极速送审,中科院2区(TOP)计算机算法类SCI,数据库稳定检索19年
算法类: 检索年份:数据库稳定检索19年 自引率:14.50% 国人占比:22.78% 期刊简介:IF:8.0-9.0,JCR1区,中科院2区(TOP) 检索情况:SCI&EI 双…...
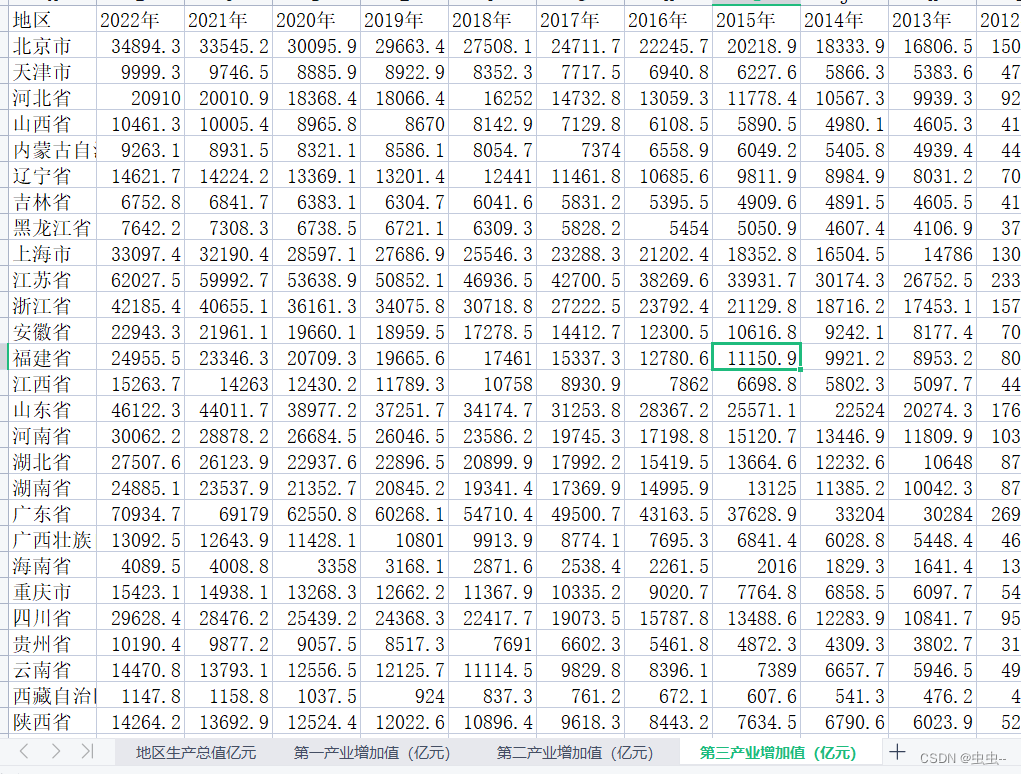
1992-2022年31省GDP、第一产业增加值、第二产业增加值 第三产业增加值
1992-2022年31省GDP、第一产业增加值、第二产业增加值 第三产业增加值 1、时间:1992-2022年 2、范围:包括31省 3、指标:省GDP、省第一产业增加值、省第二产业增加值、省第三产业增加值 4、缺失情况说明:无缺失 5、来源&#…...

100种思维模型之万物系统思维模型-57
前面我们介绍过 “万物联系思维模型” ,即万物之间存有各种各样的联系,在解决问题时要看到事物之间的连接,并找到关键的连接,继而快速的解决问题。 01 何谓万物系统思维模型 一、万物系统思维 人的思维习惯, 一…...
)
Java 中的包装类是什么?如何使用包装类来操作基本数据类型(二十二)
Java 中的包装类是一种特殊的类,用来将基本数据类型(如 int、double、char 等)包装成对象。包装类的作用是可以让基本数据类型具有对象的特性,比如可以作为参数传递给泛型类或方法,可以调用对象的方法,可以…...
【Python入门】Pycharm的使用指南
前言 📕作者简介:热爱跑步的恒川,致力于C/C、Java、Python等多编程语言,热爱跑步,喜爱音乐的一位博主。 📗本文收录于Python零基础入门系列,本专栏主要内容为Python基础语法、判断、循环语句、函…...
python搭建HaIcon物联平台!
Python是一种高级编程语言,易于学习和理解。它在各个领域都有着广泛的应用,例如数据科学、机器学习、爬虫等。 在Python的强大功能之外,Python还有着丰富的第三方库和框架,其中之一就是HaIcon。HaIcon是一种基于Python的物联网平台,它提供了完整的解决方案,包括设备管理…...
GUI编程(二)
Swing Swing是GUI(图形用户界面)开发工具包。 早期的AWT(抽象窗口工具包)组件开发的图形用户界面,要依赖本地系统,当把AWT组件开发的应用程序移植到其他平台的系统上运行时,不能保证其外观风格…...
俩小伙一晚上写了个 AI 应用,月入两万??(文末附开发教程)
开发出一款能够与 AI 对话生成和编辑思维导图的工具,听起来似乎只能是一群专业的 AI 背景团队花费大量的时间和精力训练模型,打磨应用才能完成的事情。 但是,两名大学生却在一夜之间完成了,就像炼金术士将庸俗的材料转化成黄金一…...

ES6从入门到精通:前言
ES6简介 ES6(ECMAScript 2015)是JavaScript语言的重大更新,引入了许多新特性,包括语法糖、新数据类型、模块化支持等,显著提升了开发效率和代码可维护性。 核心知识点概览 变量声明 let 和 const 取代 var…...

DockerHub与私有镜像仓库在容器化中的应用与管理
哈喽,大家好,我是左手python! Docker Hub的应用与管理 Docker Hub的基本概念与使用方法 Docker Hub是Docker官方提供的一个公共镜像仓库,用户可以在其中找到各种操作系统、软件和应用的镜像。开发者可以通过Docker Hub轻松获取所…...

《Playwright:微软的自动化测试工具详解》
Playwright 简介:声明内容来自网络,将内容拼接整理出来的文档 Playwright 是微软开发的自动化测试工具,支持 Chrome、Firefox、Safari 等主流浏览器,提供多语言 API(Python、JavaScript、Java、.NET)。它的特点包括&a…...
)
postgresql|数据库|只读用户的创建和删除(备忘)
CREATE USER read_only WITH PASSWORD 密码 -- 连接到xxx数据库 \c xxx -- 授予对xxx数据库的只读权限 GRANT CONNECT ON DATABASE xxx TO read_only; GRANT USAGE ON SCHEMA public TO read_only; GRANT SELECT ON ALL TABLES IN SCHEMA public TO read_only; GRANT EXECUTE O…...

linux 错误码总结
1,错误码的概念与作用 在Linux系统中,错误码是系统调用或库函数在执行失败时返回的特定数值,用于指示具体的错误类型。这些错误码通过全局变量errno来存储和传递,errno由操作系统维护,保存最近一次发生的错误信息。值得注意的是,errno的值在每次系统调用或函数调用失败时…...

OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别
OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别 直接训练提示词嵌入向量的核心区别 您提到的代码: prompt_embedding = initial_embedding.clone().requires_grad_(True) optimizer = torch.optim.Adam([prompt_embedding...

SpringCloudGateway 自定义局部过滤器
场景: 将所有请求转化为同一路径请求(方便穿网配置)在请求头内标识原来路径,然后在将请求分发给不同服务 AllToOneGatewayFilterFactory import lombok.Getter; import lombok.Setter; import lombok.extern.slf4j.Slf4j; impor…...

OPENCV形态学基础之二腐蚀
一.腐蚀的原理 (图1) 数学表达式:dst(x,y) erode(src(x,y)) min(x,y)src(xx,yy) 腐蚀也是图像形态学的基本功能之一,腐蚀跟膨胀属于反向操作,膨胀是把图像图像变大,而腐蚀就是把图像变小。腐蚀后的图像变小变暗淡。 腐蚀…...

AI,如何重构理解、匹配与决策?
AI 时代,我们如何理解消费? 作者|王彬 封面|Unplash 人们通过信息理解世界。 曾几何时,PC 与移动互联网重塑了人们的购物路径:信息变得唾手可得,商品决策变得高度依赖内容。 但 AI 时代的来…...
)
安卓基础(aar)
重新设置java21的环境,临时设置 $env:JAVA_HOME "D:\Android Studio\jbr" 查看当前环境变量 JAVA_HOME 的值 echo $env:JAVA_HOME 构建ARR文件 ./gradlew :private-lib:assembleRelease 目录是这样的: MyApp/ ├── app/ …...
