windows怎么把包含某个关键词的文件移动到一个文件夹中
文章目录
- windows怎么把包含某个关键词的文件移动到一个文件夹中
- 问题来源
- 省流版本
- 操作过程
- 具体问题
- 方法一:使用cmd终端解决
- 方法二:使用python脚本
- 总结
windows怎么把包含某个关键词的文件移动到一个文件夹中
问题来源
今天想移动window文件,本来想手动的,但是身为懒人,受不了这个勤奋的手指。
起初想写一个Python程序,感觉挺方便的,但是想到windows的终端都没怎么用过,除了使用conda新建环境,使用python xxx.py运行python文件。感觉其他事情一点都没做,是不是很浪费这个终端的性能啊。
我就上网查一查相关资料,如何使用windows的终端把包含某个关键词的文件移动到一个文件夹,实际上命令非常简单啊,我之前一直不知道,感觉大多数人可能和我一样都不知道。今天就写一个短文说一下,这个操作的命令是什么。
省流版本
在终端运行如下即可:
move *关键词* dir
其中关键词填写你需要批量移动的文件包含的相同关键词,dir是你要移动的目标文件夹。
操作过程
首先找到需要移动的目录文件夹,我的如下所示。可以一部分文件包含Vocals关键词,一部分文件包含Instrumental关键词。
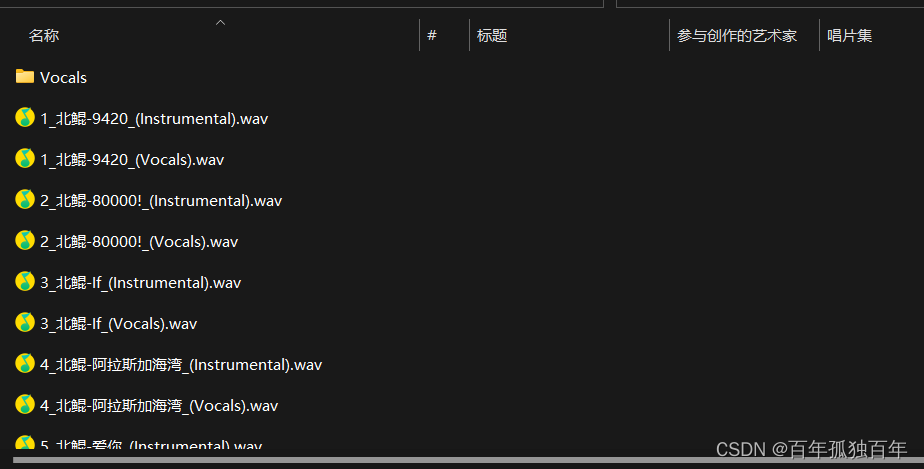
具体问题
想把包含Vocals的文件全部移动到Vocal文件夹中。
方法一:使用cmd终端解决
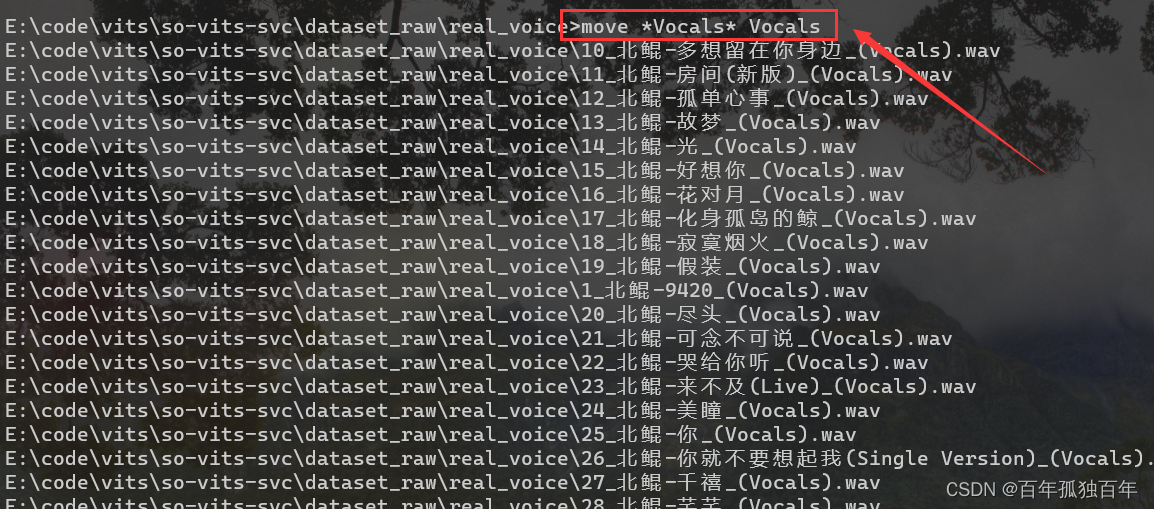
在文件夹路径输入cmd,即可在终端中打开当前目录,挺方便的。

然后使用如下命令,即可看到所有文件都已经移动到Vocals文件夹中了。
move *Vocals* Vocal
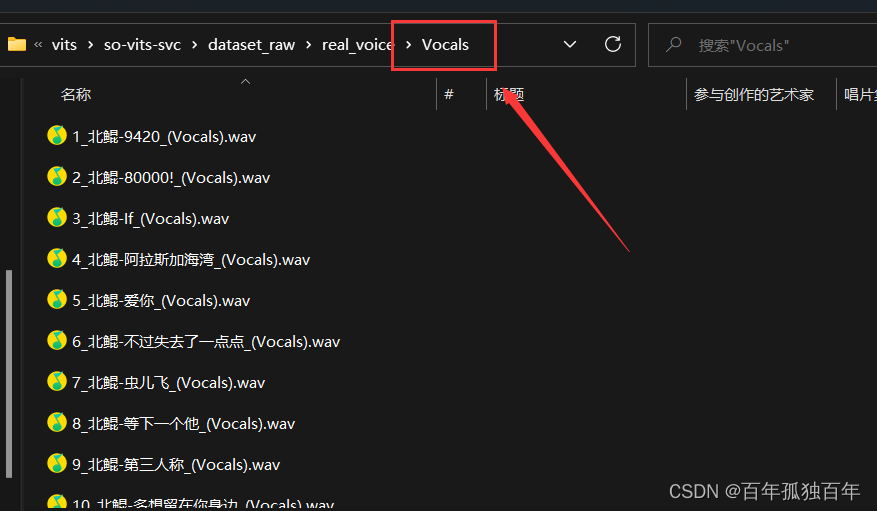
查看一下Vocals文件夹,如下,说明成功了,只把包含Vocals的文件移动了,其他的文件没有动。
是不是很简单呢!
方法二:使用python脚本
当然也可以用一个python实现该功能。
以下是一个可以在 Python 中执行的脚本,用于将当前目录中包含关键字 “Vocals” 的文件移动到名为 vocals 的子目录中:
import os
import shutil# 创建名为 vocals 的子目录
if not os.path.exists('vocals'):os.makedirs('vocals')# 搜索包含关键字 "Vocals" 的所有文件
for filename in os.listdir('.'):if 'Vocals' in filename:# 移动文件到 vocals 子目录中shutil.move(filename, 'vocals/')
该脚本首先检查当前目录中是否存在名为 “vocals” 的子目录,如果不存在,则会创建该目录。然后,它会遍历当前目录中的所有文件,并检查每个文件名是否包含关键字 “Vocals”。如果文件名包含该关键字,则将该文件移动到 “vocals” 子目录中。
请注意,运行此脚本将移动当前目录中所有包含关键字 “Vocals” 的文件,因此请确保在运行脚本之前备份所有重要文件。
总结
通过阅读本博客可以实现移动包含关键词的文件至一个文件夹,节省了大量时间,懒人癌的福音,至少是我的福音。
可以通过两种方法实现,第一个是cmd终端的命令行,第二个是通过python脚本实现,反正都挺简单的。可以自己试着玩一下。
相关文章:

windows怎么把包含某个关键词的文件移动到一个文件夹中
文章目录 windows怎么把包含某个关键词的文件移动到一个文件夹中问题来源省流版本操作过程具体问题方法一:使用cmd终端解决方法二:使用python脚本 总结 windows怎么把包含某个关键词的文件移动到一个文件夹中 问题来源 今天想移动window文件࿰…...

Unity 后处理(Post-Processing) -- (2)创建后处理配置文件
通过前面一小节,我们初步认识了后处理是什么,在Unity中简单的试了试后处理的效果。本节我们来创建一个我们自己的后处理配置文件(post-processing profile)。 一个后处理配置文件包含了一系列为了达到特定视觉效果的后处理效果的配…...

BI 商业智能和报表,傻傻分不清楚?一文给你讲透
我们经常所听到的大数据、商业智能BI、数据分析、数据挖掘等我们都统称为数据信息化。数据信息化可以帮助企业全面的了解企业的经营管理,从经验驱动到数据驱动,降低情绪、心理等主观影响,形成以数据为基础的业务决策支撑,提高决策…...
)
CSS布局基础(传统布局小结)
传统布局小结 传统布局方式标准流浮动流定位伪类元素CSS应用对象应用到自身应用到其他元素 传统布局方式 传统布局采用 标准流 浮动流 定位的方式实现布局效果,也就是通常所说的 DIV CSS 布局。 标准流 标准流中的元素在 页面默认的 维度,块级元素…...

【五一创作】Qt quick基础1(包含基本元素Text Image Rectangle的使用)
Qt quick基础1(包含基本元素Text Image Rectangle的使用) 目录 Qt quick基础1(包含基本元素Text Image Rectangle的使用)前言qt中有直接设计ui的拖拽式的widget,为什么还需要Qtquick?QML语言Qt 版本创建一个Qt quick项…...

LVS+Keepalived 高可用群集部署
一、LVSKeepalived 高可用群集 在这个高度信息化的 IT 时代,企业的生产系统、业务运营、销售和支持,以及日常管理等环节越来越依赖于计算机信息和服务,对高可用(HA)技术的应用需求不断提高,以便提供持续的…...
小黑子—Java从入门到入土过程:第八章
Java零基础入门8.0 Java系列第八章1. 双列集合 Map1.1 Map 集合中常见的API1.2 Map 集合的遍历方式1.2 - I 第一种遍历方式:键找值KeySet 方法1.2 - II 第二种遍历方式:键值对 entrySet 方法1.2 - III 第三种遍历方式:lambda表达式 1.3 HashM…...

innodb_flush_log_at_trx_commit 和 sync_binlog 参数解析
这两个参数和MySQL的一致性以及性能相关,默认配置大多数情况下不是最优的。一般来说,互联网线上系统的配置: innodb_flush_log_at_trx_commit —— 0 sync_binlog —— 1000 一、innodb_flush_log_at_trx_commit 事务提交刷盘时机 如果我…...

hd debug - DAPLink的资料
文章目录 DAPLink的资料概述笔记库迁出的技巧END DAPLink的资料 概述 查资料时, 看到有DAPLink的资料, 记录一下. 笔记 DAPLink项目分为软件和硬件2部分, 不在一个库中. 总览 : https://daplink.io/ 这个页面上说了软件和硬件项目的库地址. 软件库地址 : https://github.…...

Android adb常用50条命令
1. adb devices - 列出所有连接的 Android 设备及模拟器 2. adb shell - 启动 Android 设备或模拟器的 shell 终端 3. adb install - 安装 APK 文件 4. adb uninstall - 卸载 APK 文件 5. adb logcat - 查看日志输出信息,用于调试应用 6. adb push - 将文件推送到 Andro…...
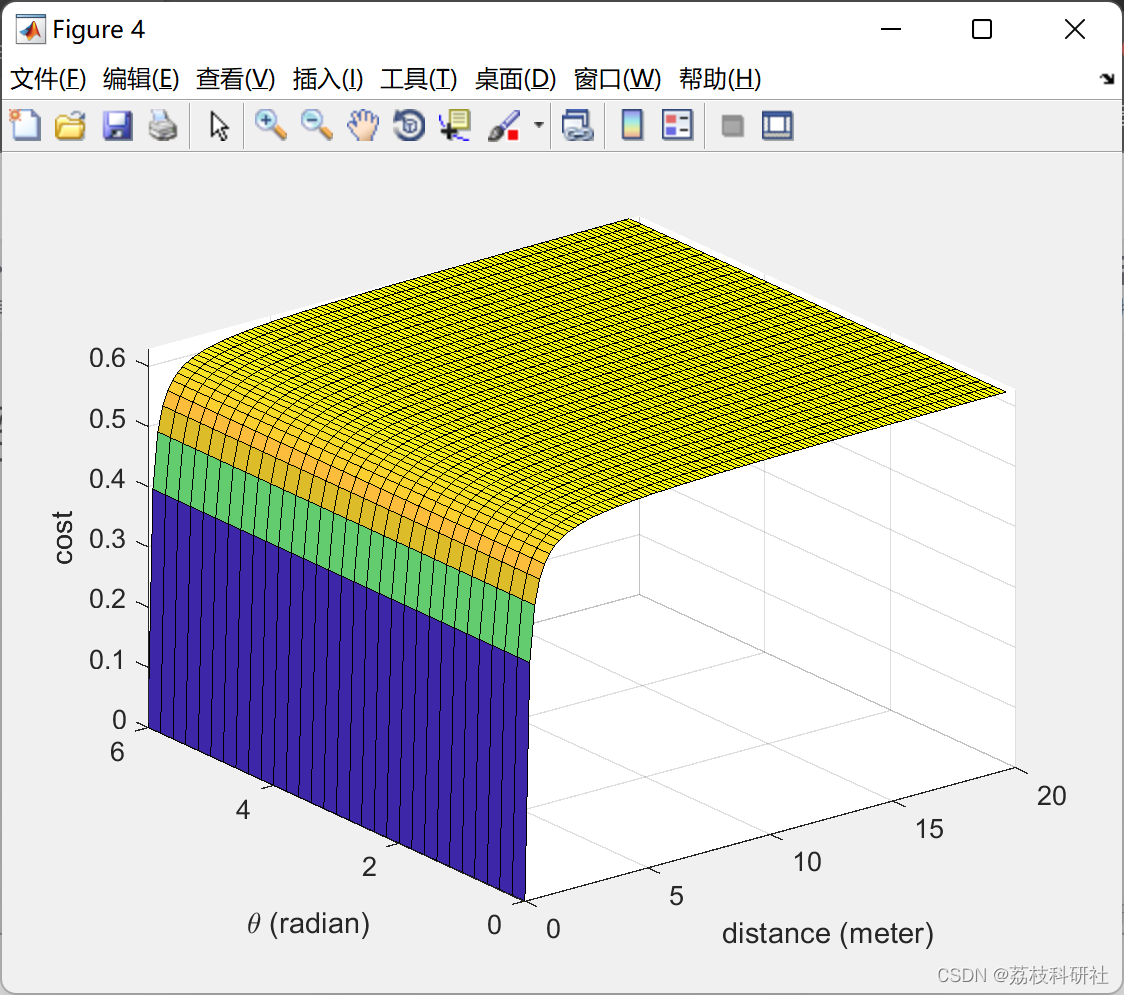
【无人车】无人驾驶地面车辆避障研究(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...

Visual Studio高效调试手段与调试技巧总结
目录 1、对0xCCCCCCCC、0xCDCDCDCD和0xFEEEFEEE等常见异常值的辨识度 2、在Debug下遇到报错弹框,点击重试,查看函数调用堆栈...

Day37 Map集合
Map集合 Map集合是接口,interface Map <K , V> K:键的类型; V:值的类型 将键映射到值得对象;不能包含重复的键;每个键可以映射到最多一个值。例如:001 令狐冲 ; 002 岳不群 ; …...

是人就能学会的Spring源码教学-Spring的简单使用
是人就能学会的Spring源码教学-Spring的简单使用 Spring的最简单入门使用第一步 创建项目第二步 配置项目第三步 启动项目 Spring的最简单入门使用 各位道友且跟我一道来学习Spring的最简单的入门使用,为了方便和简单,我使用了Spring Boot项目ÿ…...
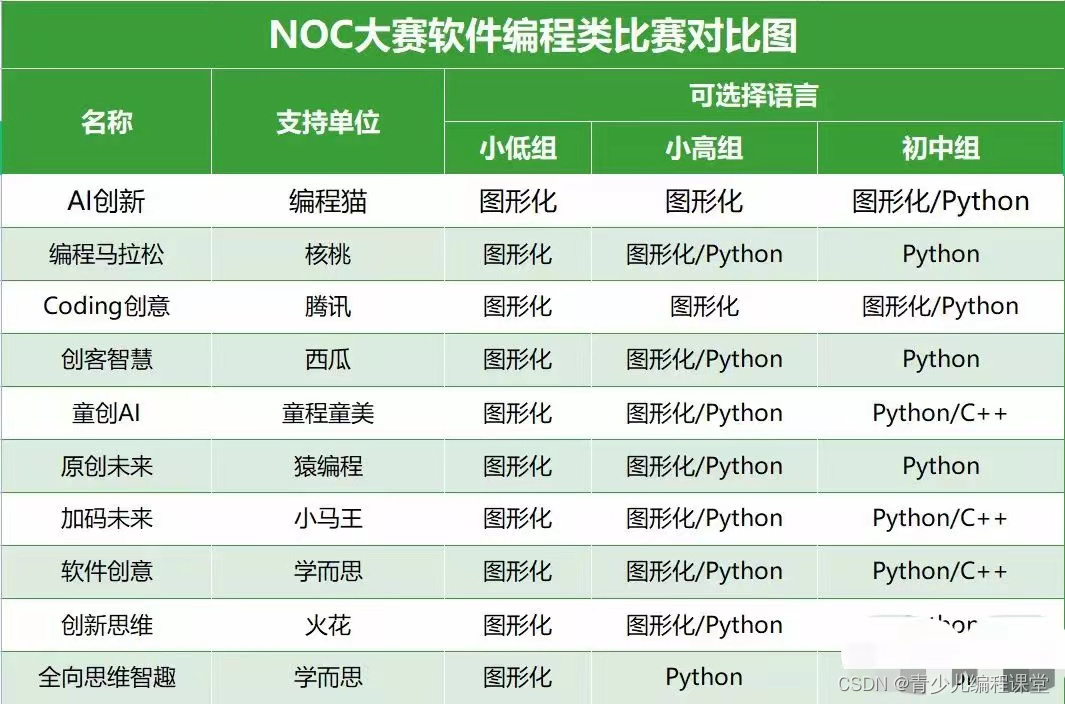
NOC大赛·核桃编程马拉松赛道知识点大纲(高年级及初中组)
NOC核桃编程马拉松知识点大纲(高年级及初中组) (一)基础语法 1.掌握运动积木的用法。 包括“移动 10 步”、“左/右转 X 度”、“面向 X 方向/鼠标指针/ 角色”、“移到 XY 坐标/鼠标/角色”、“X/Y 坐标的设定和增加”、 “滑行到 XY/鼠标/角色”等积木用法,详细如下。 1…...
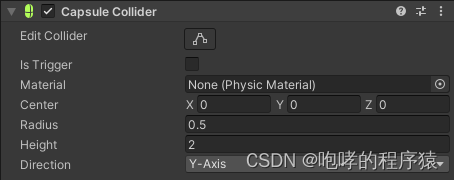
第二十六章 Unity碰撞体Collision(上)
在游戏世界中,游戏物体之间的交互都是通过“碰撞接触”来进行交互的。例如,攻击怪物则是主角与怪物的碰撞,触发机关则是主角与机关的碰撞。在DirectX课程中,我们也大致介绍过有关碰撞检测的内容。游戏世界中的3D模型的形状是非常复…...

Qt Installer Framework使用教程:
步骤一: 下载并安装Qt Installer Framework工具 http://download.qt.io/official_releases/qt-installer-framework/ 将安装目录添加到环境变量,如安装D盘时D:\Qt\QtIFW-4.5.0\bin 步骤二: 将测试例子(如D:\Qt\QtIFW-4.5.0\…...
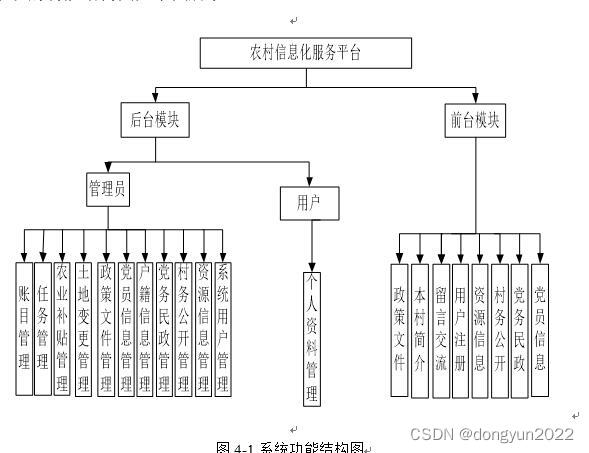
nodejs+vue+java农村信息化服务平台
用户的登录模块:用户登录本系统,对个人的信息等进行查询,操作可使用的功能。 用户注册模块:游客用户可以进行用户注册,系统会反馈是否注册成功。 添加管理员模块:向本系统中添加更多的管理人员,…...

代码随想录补打卡 62不同路径 63 不同路径2
代码如下 func uniquePaths(m int, n int) int { dp : make([][]int,m) //定义一个二维数组 for i : 0 ; i < m ; i { //遍历这个二维数组的每个元素,并将每个元素都定义为一个一维数组 dp[i] make([]int,n) //这样就生成了图中的一个二维网格 dp[i][0] …...

树的存储和遍历
文章目录 6.5 树与森林6.5.1 树的存储结构1. 双亲表示法(顺序存储结构)2 孩子链表表示法3 孩子兄弟表示法(二叉树表示法) 6.5.2 森林与二叉树的转换1 树转换成二叉树2 二叉树转换成树3 森林转换成二叉树4 二叉树转换成森林 6.5.3 树和森林的遍历1. 树的遍历2. 森林的遍历 6.6 赫…...

IDEA运行Tomcat出现乱码问题解决汇总
最近正值期末周,有很多同学在写期末Java web作业时,运行tomcat出现乱码问题,经过多次解决与研究,我做了如下整理: 原因: IDEA本身编码与tomcat的编码与Windows编码不同导致,Windows 系统控制台…...

挑战杯推荐项目
“人工智能”创意赛 - 智能艺术创作助手:借助大模型技术,开发能根据用户输入的主题、风格等要求,生成绘画、音乐、文学作品等多种形式艺术创作灵感或初稿的应用,帮助艺术家和创意爱好者激发创意、提高创作效率。 - 个性化梦境…...

【JavaEE】-- HTTP
1. HTTP是什么? HTTP(全称为"超文本传输协议")是一种应用非常广泛的应用层协议,HTTP是基于TCP协议的一种应用层协议。 应用层协议:是计算机网络协议栈中最高层的协议,它定义了运行在不同主机上…...

macOS多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用
文章目录 问题现象问题原因解决办法 问题现象 macOS启动台(Launchpad)多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用。 问题原因 很明显,都是Google家的办公全家桶。这些应用并不是通过独立安装的…...

AI书签管理工具开发全记录(十九):嵌入资源处理
1.前言 📝 在上一篇文章中,我们完成了书签的导入导出功能。本篇文章我们研究如何处理嵌入资源,方便后续将资源打包到一个可执行文件中。 2.embed介绍 🎯 Go 1.16 引入了革命性的 embed 包,彻底改变了静态资源管理的…...

#Uniapp篇:chrome调试unapp适配
chrome调试设备----使用Android模拟机开发调试移动端页面 Chrome://inspect/#devices MuMu模拟器Edge浏览器:Android原生APP嵌入的H5页面元素定位 chrome://inspect/#devices uniapp单位适配 根路径下 postcss.config.js 需要装这些插件 “postcss”: “^8.5.…...

力扣热题100 k个一组反转链表题解
题目: 代码: func reverseKGroup(head *ListNode, k int) *ListNode {cur : headfor i : 0; i < k; i {if cur nil {return head}cur cur.Next}newHead : reverse(head, cur)head.Next reverseKGroup(cur, k)return newHead }func reverse(start, end *ListNode) *ListN…...

uniapp 字符包含的相关方法
在uniapp中,如果你想检查一个字符串是否包含另一个子字符串,你可以使用JavaScript中的includes()方法或者indexOf()方法。这两种方法都可以达到目的,但它们在处理方式和返回值上有所不同。 使用includes()方法 includes()方法用于判断一个字…...

SQL Server 触发器调用存储过程实现发送 HTTP 请求
文章目录 需求分析解决第 1 步:前置条件,启用 OLE 自动化方式 1:使用 SQL 实现启用 OLE 自动化方式 2:Sql Server 2005启动OLE自动化方式 3:Sql Server 2008启动OLE自动化第 2 步:创建存储过程第 3 步:创建触发器扩展 - 如何调试?第 1 步:登录 SQL Server 2008第 2 步…...
)
华为OD最新机试真题-数组组成的最小数字-OD统一考试(B卷)
题目描述 给定一个整型数组,请从该数组中选择3个元素 组成最小数字并输出 (如果数组长度小于3,则选择数组中所有元素来组成最小数字)。 输入描述 行用半角逗号分割的字符串记录的整型数组,0<数组长度<= 100,0<整数的取值范围<= 10000。 输出描述 由3个元素组成…...
