算法刷题打卡第90天:表现良好的最长时间段
表现良好的最长时间段
难度:中等
给你一份工作时间表 hours,上面记录着某一位员工每天的工作小时数。
我们认为当员工一天中的工作小时数大于 8 小时的时候,那么这一天就是「劳累的一天」。
所谓「表现良好的时间段」,意味在这段时间内,「劳累的天数」是严格 大于「不劳累的天数」。
请你返回「表现良好时间段」的最大长度。
示例 1:
输入:hours = [9,9,6,0,6,6,9]
输出:3
解释:最长的表现良好时间段是 [9,9,6]。
示例 2:
输入:hours = [6,6,6]
输出:0
前置知识:前缀和
对于数组 nums\textit{nums}nums,定义它的前缀和 s[0]=0\textit{s}[0]=0s[0]=0,s[i+1]=∑j=0inums[j]。\textit{s}[i+1] = \sum\limits_{j=0}^{i}\textit{nums}[j]。s[i+1]=j=0∑inums[j]。
例如 nums=[1,2,−1,2]\textit{nums}=[1,2,-1,2]nums=[1,2,−1,2],对应的前缀和数组为 s=[0,1,3,2,4]s=[0,1,3,2,4]s=[0,1,3,2,4]。
通过前缀和,我们可以把子数组的元素和转换成两个前缀和的差,即
∑j=leftrightnums[j]=∑j=0rightnums[j]−∑j=0left−1nums[j]=s[right+1]−s[left]\sum_{j=\textit{left}}^{\textit{right}}\textit{nums}[j] = \sum\limits_{j=0}^{\textit{right}}\textit{nums}[j] - \sum\limits_{j=0}^{\textit{left}-1}\textit{nums}[j] = \textit{s}[\textit{right}+1] - \textit{s}[\textit{left}] j=left∑rightnums[j]=j=0∑rightnums[j]−j=0∑left−1nums[j]=s[right+1]−s[left]
例如 nums\textit{nums}nums的子数组 [2,−1,2][2,-1,2][2,−1,2] 的和就可以用 s[4]−s[1]=4−1=3s[4]-s[1]=4-1=3s[4]−s[1]=4−1=3 算出来。
注:为方便计算,常用左闭右开区间 [left,right)[\textit{left},\textit{right})[left,right) 来表示子数组,此时子数组的和为 s[right]−s[left]\textit{s}[\textit{right}] - \textit{s}[\textit{left}]s[right]−s[left],子数组的长度为 right−left\textit{right}-\textit{left}right−left。
方法一:单调栈
思路:
先把问题转换到我们熟悉的东西上。
「劳累天数大于不劳累天数」等价于「劳累天数减去不劳累天数大于 000」。
那么把劳累的一天视作 nums[i]=1\textit{nums}[i]=1nums[i]=1,不劳累的一天视作 nums[i]=−1\textit{nums}[i]=-1nums[i]=−1,则问题变为:
计算 nums\textit{nums}nums 的最长子数组,其元素和大于 000。
既然说到了「子数组的元素和」,那么利用前缀和 sss,将问题变为:
找到两个下标 iii 和 jjj,满足 j<ij<ij<i 且 s[j]<s[i]s[j]<s[i]s[j]<s[i],最大化 i−ji-ji−j 的值。
想一想,哪些值可以作为 jjj(最长子数组的左端点)呢?
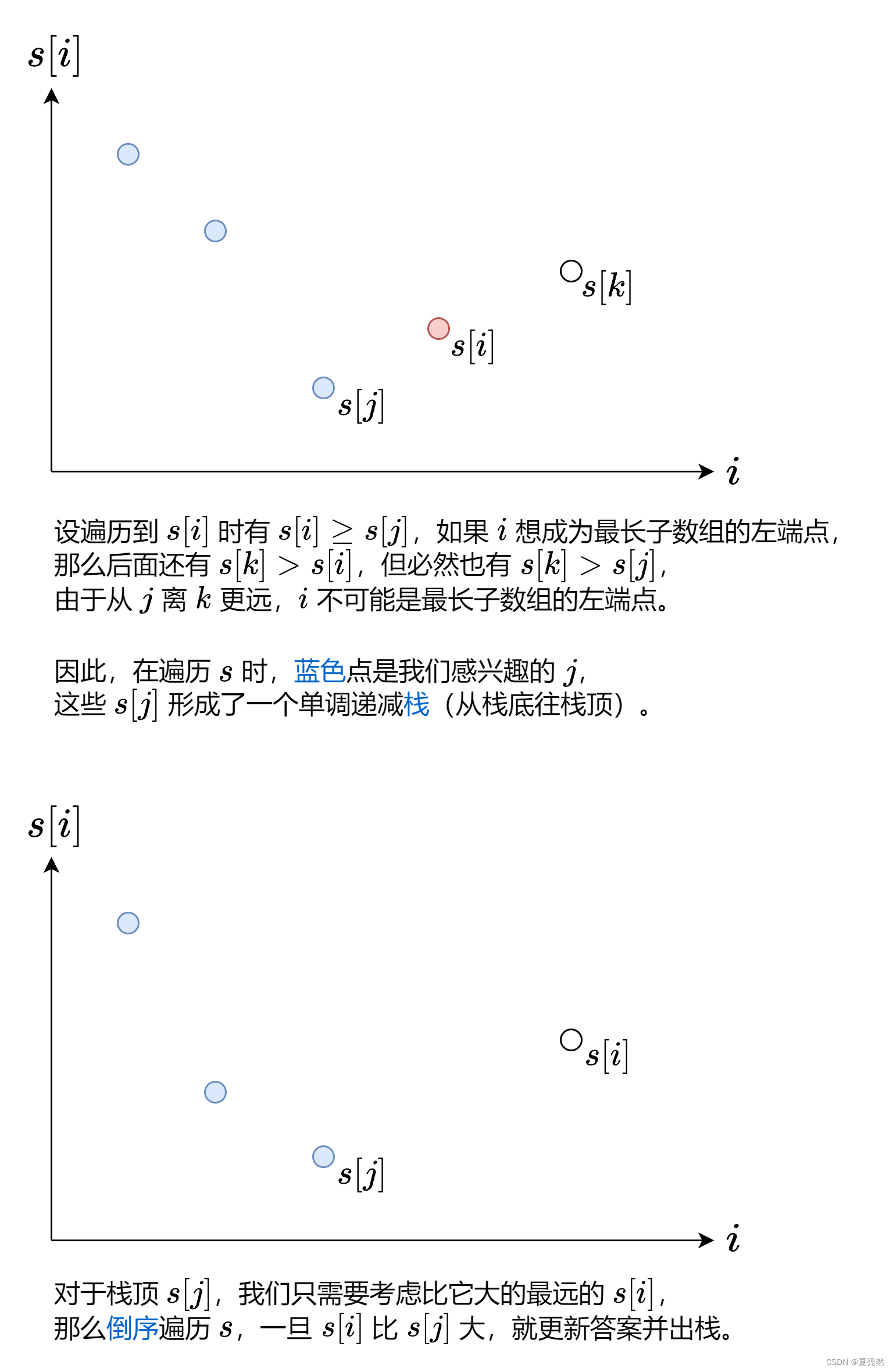
复杂度分析:
- 时间复杂度: O(n)O(n)O(n),其中 nnn 为 hours\textit{hours}hours的长度。注意每个元素至多入栈出栈各一次,因此二重循环的时间复杂度是 O(n)O(n)O(n) 的。
- 空间复杂度: O(n)O(n)O(n)。
class Solution:def longestWPI(self, hours: List[int]) -> int:hours_sum, start = [0] * (len(hours) + 1), [0]for i in range(len(hours)):# 前缀和hours_sum[i+1] = hours_sum[i] + 1 if hours[i] > 8 else hours_sum[i] - 1# 可能是开头的位置if hours_sum[start[-1]] > hours_sum[i+1]:start.append(i+1)res = 0for i in range(len(hours), 0, -1):while start and hours_sum[i] > hours_sum[start[-1]]:res = max(res, i - start.pop())return res
方法二:利用前缀和的连续性
虽说方法一更加通用,不过利用 nums\textit{nums}nums中只有 111 和 −1−1−1 的特点,可以做到一次遍历。
考虑 s[i]s[i]s[i]:
- 如果 s[i]>0s[i]>0s[i]>0,那么 j=0j=0j=0 就是最远的左端点,因为 s[0]=0s[0]=0s[0]=0,故 s[i]−s[0]=s[i]>0s[i]-s[0]=s[i]>0s[i]−s[0]=s[i]>0,符合要求。
- 如果 s[i]≤0s[i]\le 0s[i]≤0,那么 jjj 就是 s[i]−1s[i]-1s[i]−1 首次出现的位置。为什么是 s[i]−1s[i]-1s[i]−1 而不是其它更小的数?这是因为前缀和是从 000 开始的,由于 nums\textit{nums}nums 中只有 111 和 −1−1−1,那么相邻前缀和的差都恰好为 111,要想算出比 s[i]−1s[i]-1s[i]−1 更小的数,必然会先算出 s[i]−1s[i]-1s[i]−1,那么这些更小数必然在 s[i]−1s[i]-1s[i]−1 首次出现的位置的右边。
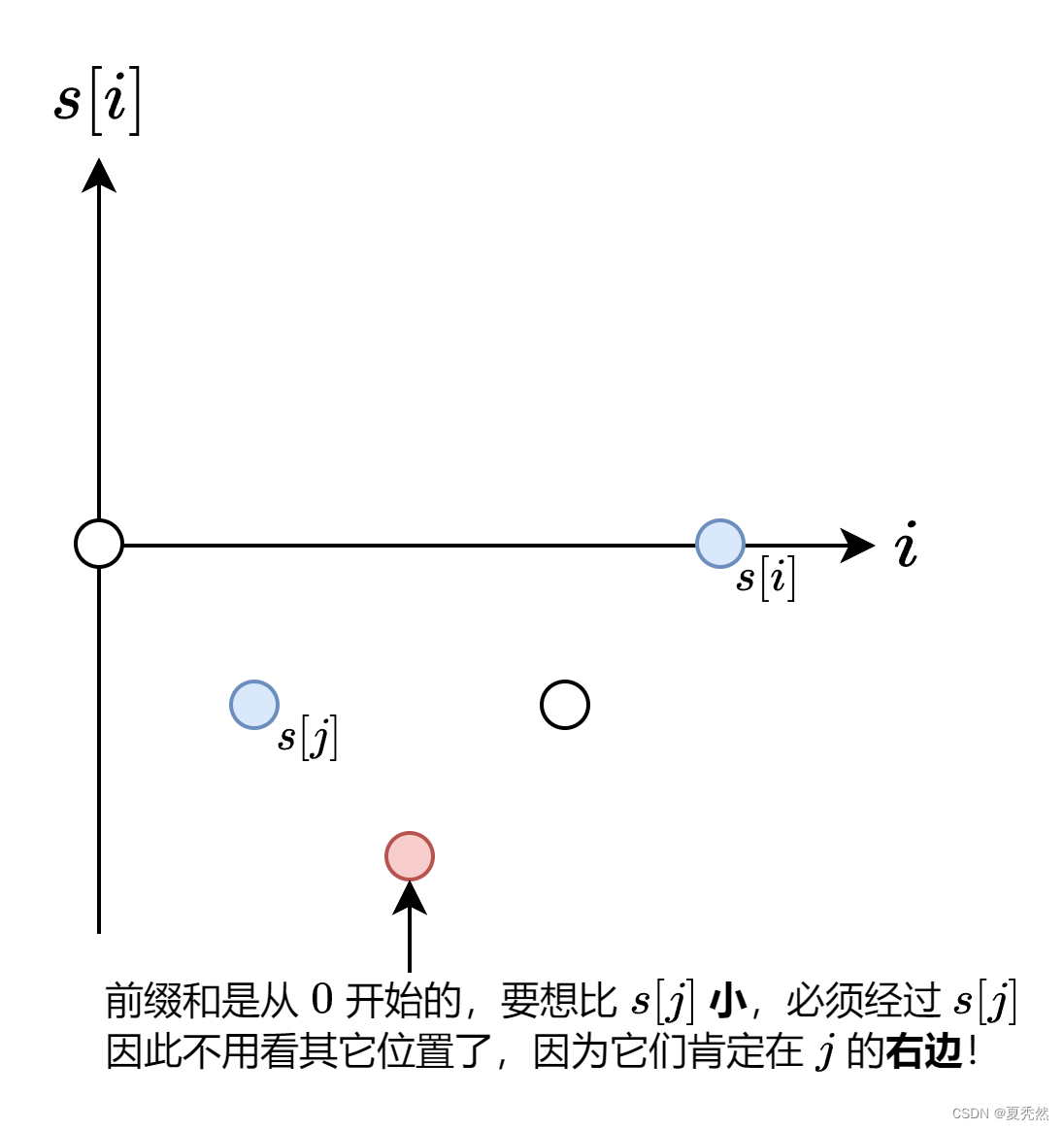
代码实现时,可以用哈希表记录每个 s[i]s[i]s[i] 首次出现的下标。
不过,由于我们只需要考虑值在闭区间 [−n,0][-n,0][−n,0] 内的前缀和,用数组记录是更加高效的。同时,为了避免用负数访问数组,可以在计算过程中把前缀和取反。
复杂度分析:
- 时间复杂度: O(n)O(n)O(n),其中 nnn 为 hours\textit{hours}hours的长度。
- 空间复杂度: O(n)O(n)O(n)。
class Solution:def longestWPI(self, hours: List[int]) -> int:pos = [0] * (len(hours) + 2) # 记录前缀和首次出现的位置res = sums = 0for i, j in enumerate(hours, 1):sums += -1 if j > 8 else 1 # 取反,改为减法if sums < 0:res = ielse:if pos[sums+1]: # 原本是 sums-1,取反改为 sums+1res = max(res, i-pos[sums+1]) # 这里手写 if 会更快if pos[sums] == 0:pos[sums] = ireturn res
来源:力扣(LeetCode)
链接:https://leetcode.cn/problems/longest-well-performing-interval/solutions/2110211/liang-chong-zuo-fa-liang-zhang-tu-miao-d-hysl/
相关文章:

算法刷题打卡第90天:表现良好的最长时间段
表现良好的最长时间段 难度:中等 给你一份工作时间表 hours,上面记录着某一位员工每天的工作小时数。 我们认为当员工一天中的工作小时数大于 8 小时的时候,那么这一天就是「劳累的一天」。 所谓「表现良好的时间段」,意味在这…...
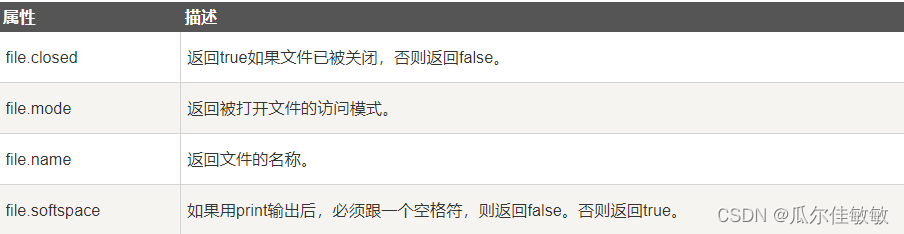
Python语言零基础入门教程(十七)
Python 文件I/O 本章只讲述所有基本的 I/O 函数,更多函数请参考Python标准文档。 #### 打印到屏幕 最简单的输出方法是用print语句,你可以给它传递零个或多个用逗号隔开的表达式。此函数把你传递的表达式转换成一个字符串表达式,并将结果写…...
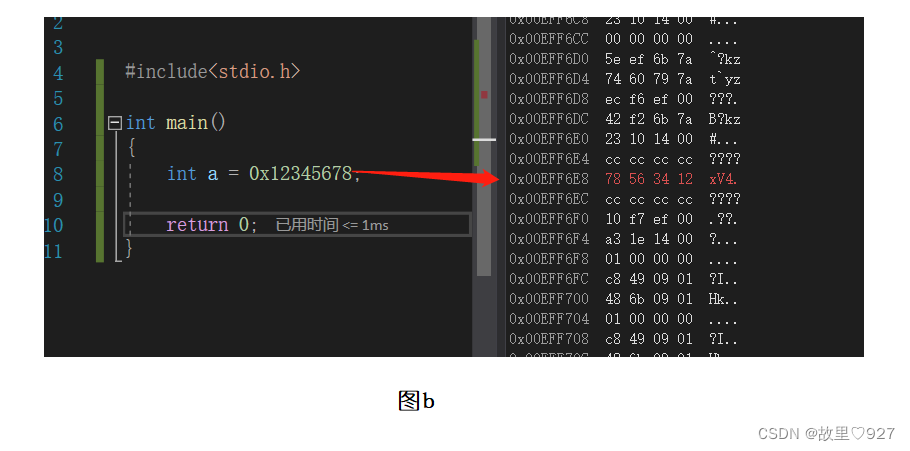
C语言中大小端问题
目录 一、什么是大小端 二、 举个例子 三、大小端演示 四、解释"二"中举例的问题 五、怎么判断是大端还是小端 六、一个题目 一、什么是大小端 大端模式(大端字节序存储):就是高位字节数据存放在内存的低地址端ÿ…...
vue2+微前端qiankun从搭建到部署的实践(主子应用切换;集成vue3+vite3子应用)
一、最终效果 二、微前端(qiankun)介绍及为什么选择用微前端,可以看官网 三、目录结构如下 四、具体配置 一、主应用配置 1、主应用技术栈 Vue-cli4搭建项目Vue2Element-Uiqiankun;Vue2Element-Uiqiankun 2、搭建好主项目&…...

怎么代理微信小程序创业?
随着微信的兴起,小程序已经成为了人们生活中不可或缺的一部分。如果你想要创业的话,那么代理微信小程序是一个不错的选择。本文将为大家介绍怎么代理微信小程序创业。 一、什么是微信小程序 微信小程序是一款专为移动设备使用者而设计的应用。它通过扫…...

今天是情人节呐,我利用Python制作了好多表白的东西,快来吧~
今天是情人节那,有没有现在没有对象的宝子,评论里扣个111哈哈 目录 玫瑰 爱心树 丘比特 多彩气球 阿玥的小课堂 一、情人节的由来 二、情人节的来历和意义 玫瑰 局部代码实现如下: # 花瓣1 turtle.left(150) turtle.circle(-90, 70) …...
【Linux】-- 进程信号(处理、内核)
上篇:【Linux】-- 进程信号(认识、应用)_川入的博客-CSDN博客 目录 信号其他相关常见概念 pending handler block 信号处理的过程 sigset_t sigset_t使用 系统接口 sigpending sigprocmask 捕捉方法 sigaction struct sigactio …...
C/【静态通讯录】
🌱博客主页:大寄一场. 🌱系列专栏:C语言学习笔记 😘博客制作不易欢迎各位👍点赞⭐收藏➕关注 前言 往期回顾: C/扫雷 C/N子棋 通讯录作为通讯录地址的书本,当今的通讯录可以涵盖多项…...

万卷书 - 让孩子对自己负责 [The Self-Driven Child]
让孩子对自己负责 The Self-Driven Child - 让你的孩子更加科学合理的掌控自己的生活 简介 《The Self-Driven Child》(2018)解释了我们对孩子的习惯性控制欲,它导致了孩子压力过大、难以合作,以及主观能动性差。本书不提倡这种做法,而是认为我们应该帮助孩子自己做出合适…...
Postman中cookie的操作
在接口测试中,某些接口的调用,需要带入已有Cookie,比如有些接口需要登陆后才能访问。 Postman接口请求使用Cookie有如下两种方式: 1、直接在头域中添加Cookie头域,适用于已经知道请求所用Cookie数据的情况。 2、使用…...
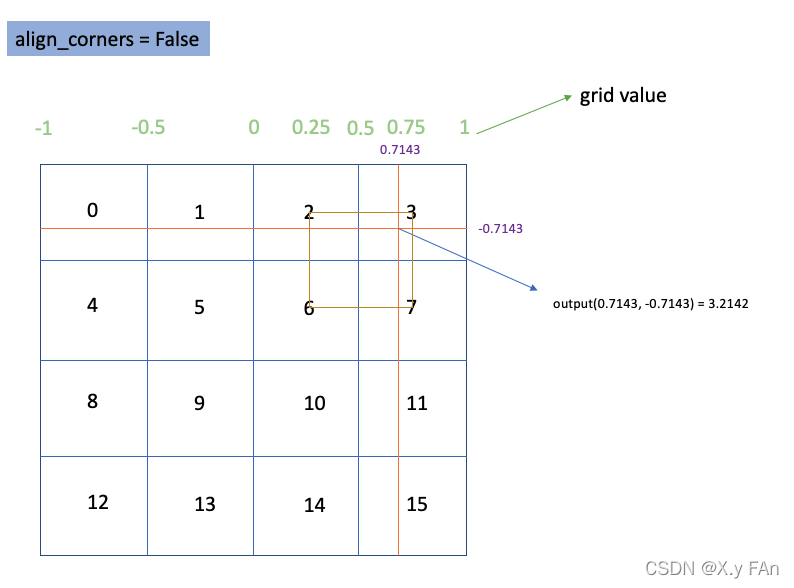
torch.grid_sample
参考: 双线性插值的理论Pytorch grid_sample解析PyTorch中grid_sample的使用方法pytorch中的grid_sample()使用 查阅官方文档,TORCH.NN.FUNCTIONAL.GRID_SAMPLE grid_sample的函数签名如下所示,torch.nn.functional.grid_sample(input, gr…...
前端基于 Docker 的 SSR 持续开发集成环境实践
项目收益 整体开发效率提升20%。加快首屏渲染速度,减少白屏时间,弱网环境下页面打开速度提升40%。 权衡 在选择使用SSR之前,需要考虑以下事项! SSR需要可以运行Node.js的服务器,学习成本相对较高。对于服务器而言&a…...

ARM交叉编译入门及交叉编译第三方库常见问题解析
1. 交叉编译是什么? 交叉编译简单说来,就是编译成果物的地儿不是你运行这个成果物的地儿。最常见的场景,就是我们要编译一个 ARM版本 的可执行程序,但我们编译这个 ARM版本 可执行程序的地方,是在一个 x86_x64 的平台…...

Ruby Web Service 应用 - SOAP4R
什么是 SOAP? 简单对象访问协议(SOAP,全写为Simple Object Access Protocol)是交换数据的一种协议规范。 SOAP 是一种简单的基于 XML 的协议,它使应用程序通过 HTTP 来交换信息。 简单对象访问协议是交换数据的一种协议规范,是一种轻量的、…...
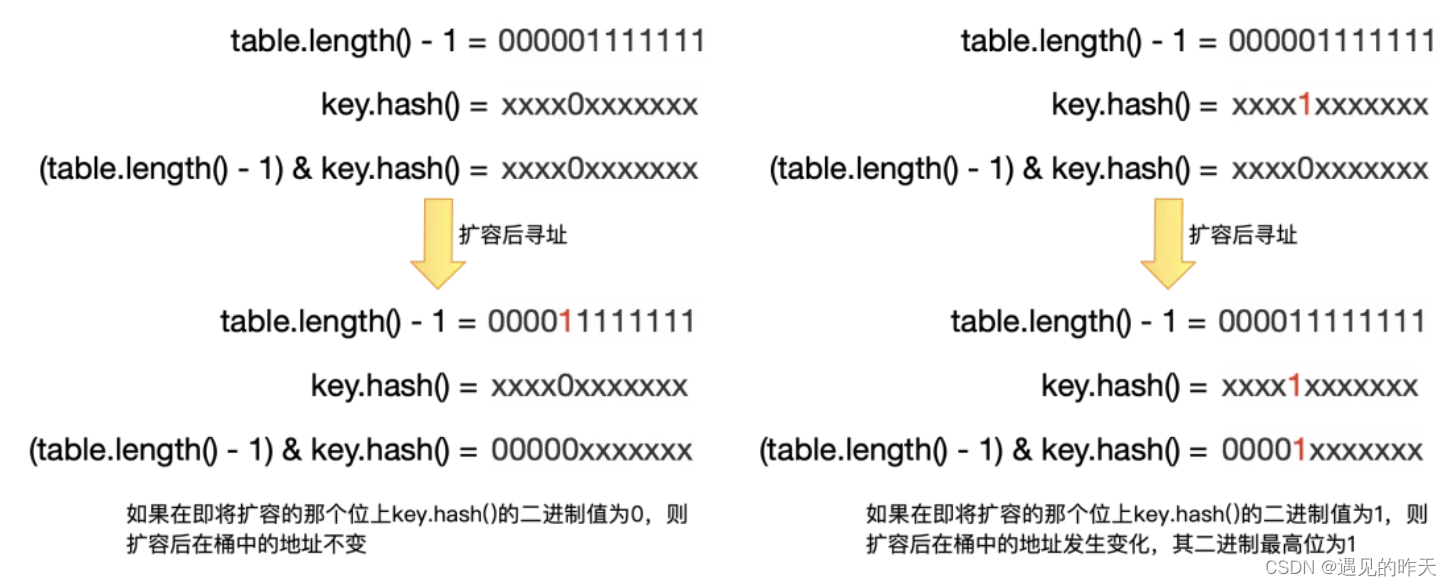
HashMap底层实现原理概述
原文https://blog.csdn.net/fedorafrog/article/details/115478407 hashMap结构 常见问题 在理解了HashMap的整体架构的基础上,我们可以试着回答一下下面的几个问题,如果对其中的某几个问题还有疑惑,那就说明我们还需要深入代码,…...
Linux驱动学习环境搭建
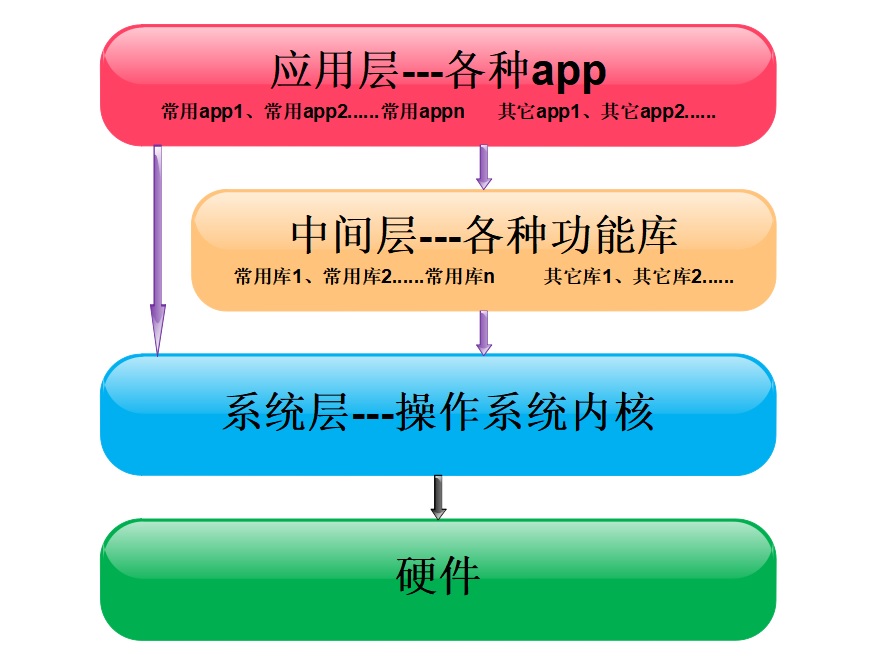
背景常识 一、程序分类 程序按其运行环境分为: 1. 裸机程序:直接运行在对应硬件上的程序 2. 应用程序:只能运行在对应操作系统上的程序 二、计算机系统的层次结构 所有智能设备其实都是计算机,机顶盒、路由器、冰箱、洗衣机、汽…...

Java基础之异常
目录1 异常1.1 异常的概述1.2 常见异常类型1.3 JVM的默认处理方案1.4 编译时异常的处理方式1.4.1 异常处理之 try ... catch ... [ktʃ](捕获异常)1.4.2 异常处理之 throws(抛出异常)1.5 Throwable 的成员方法1.6 编译时异常和运行…...

感慨:大三了,未来该何去何从呢
笔者曾在十一月份通过了字节跳动的三次面试, 但是最终因为疫情原因不能满足公司的入职时间要求, 没有拿到offer。近期也是投递了大量大厂的实习岗, 但是要么已读不回, 要么明确告诉我学历至少要985硕士(天天被阿里cpu)。 说实话一…...
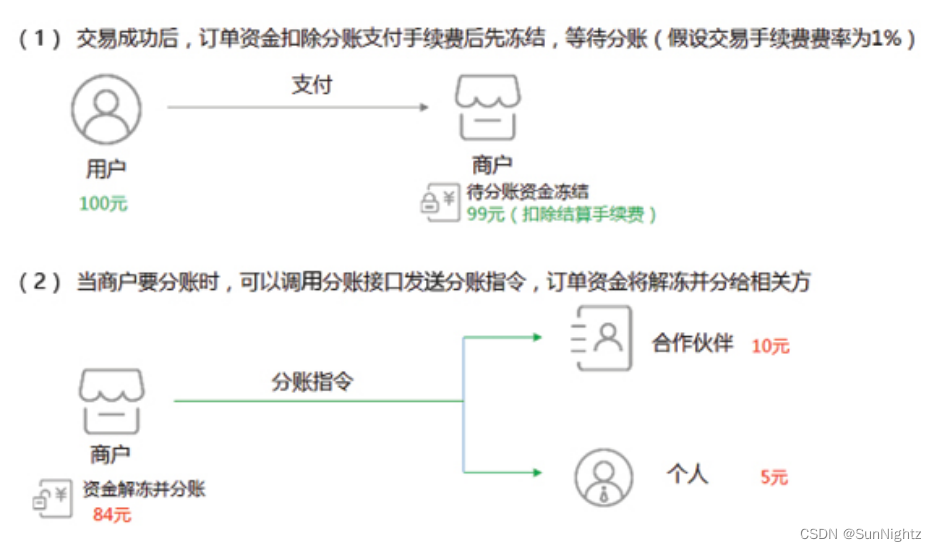
分账系统逻辑
一、说明 主体与业务关系方进行相关利益和支出的分配过程 使用场景: 在分销业务中,主营商户收到用户购买分销商品所支付的款项后,可以通过分账逻辑,与分销商进行佣金结算。在零售、餐饮等行业中,当销售人员完零售等…...

SpringCloud篇——什么是SpringCloud、有什么优缺点、学习顺序是什么
文章目录一、首先看官方解释二、Spring Cloud 的项目的位置三、Spring Cloud的子项目四、Spring Cloud 现状五、spring cloud 优缺点六、Spring Cloud 和 Dubbo 对比七、Spring Cloud 学习路线一、首先看官方解释 Spring Cloud为开发人员提供了快速构建分布式系统中一些常见模式…...

Docker 离线安装指南
参考文章 1、确认操作系统类型及内核版本 Docker依赖于Linux内核的一些特性,不同版本的Docker对内核版本有不同要求。例如,Docker 17.06及之后的版本通常需要Linux内核3.10及以上版本,Docker17.09及更高版本对应Linux内核4.9.x及更高版本。…...

Prompt Tuning、P-Tuning、Prefix Tuning的区别
一、Prompt Tuning、P-Tuning、Prefix Tuning的区别 1. Prompt Tuning(提示调优) 核心思想:固定预训练模型参数,仅学习额外的连续提示向量(通常是嵌入层的一部分)。实现方式:在输入文本前添加可训练的连续向量(软提示),模型只更新这些提示参数。优势:参数量少(仅提…...

屋顶变身“发电站” ,中天合创屋面分布式光伏发电项目顺利并网!
5月28日,中天合创屋面分布式光伏发电项目顺利并网发电,该项目位于内蒙古自治区鄂尔多斯市乌审旗,项目利用中天合创聚乙烯、聚丙烯仓库屋面作为场地建设光伏电站,总装机容量为9.96MWp。 项目投运后,每年可节约标煤3670…...

数据库分批入库
今天在工作中,遇到一个问题,就是分批查询的时候,由于批次过大导致出现了一些问题,一下是问题描述和解决方案: 示例: // 假设已有数据列表 dataList 和 PreparedStatement pstmt int batchSize 1000; // …...

AspectJ 在 Android 中的完整使用指南
一、环境配置(Gradle 7.0 适配) 1. 项目级 build.gradle // 注意:沪江插件已停更,推荐官方兼容方案 buildscript {dependencies {classpath org.aspectj:aspectjtools:1.9.9.1 // AspectJ 工具} } 2. 模块级 build.gradle plu…...

DeepSeek 技术赋能无人农场协同作业:用 AI 重构农田管理 “神经网”
目录 一、引言二、DeepSeek 技术大揭秘2.1 核心架构解析2.2 关键技术剖析 三、智能农业无人农场协同作业现状3.1 发展现状概述3.2 协同作业模式介绍 四、DeepSeek 的 “农场奇妙游”4.1 数据处理与分析4.2 作物生长监测与预测4.3 病虫害防治4.4 农机协同作业调度 五、实际案例大…...

云原生安全实战:API网关Kong的鉴权与限流详解
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 一、基础概念 1. API网关(API Gateway) API网关是微服务架构中的核心组件,负责统一管理所有API的流量入口。它像一座…...

nnUNet V2修改网络——暴力替换网络为UNet++
更换前,要用nnUNet V2跑通所用数据集,证明nnUNet V2、数据集、运行环境等没有问题 阅读nnU-Net V2 的 U-Net结构,初步了解要修改的网络,知己知彼,修改起来才能游刃有余。 U-Net存在两个局限,一是网络的最佳深度因应用场景而异,这取决于任务的难度和可用于训练的标注数…...

0x-3-Oracle 23 ai-sqlcl 25.1 集成安装-配置和优化
是不是受够了安装了oracle database之后sqlplus的简陋,无法删除无法上下翻页的苦恼。 可以安装readline和rlwrap插件的话,配置.bahs_profile后也能解决上下翻页这些,但是很多生产环境无法安装rpm包。 oracle提供了sqlcl免费许可,…...

Android写一个捕获全局异常的工具类
项目开发和实际运行过程中难免会遇到异常发生,系统提供了一个可以捕获全局异常的工具Uncaughtexceptionhandler,它是Thread的子类(就是package java.lang;里线程的Thread)。本文将利用它将设备信息、报错信息以及错误的发生时间都…...
