Python每日一练(20230507) 丑数I\II\III、超级丑数

目录
1. 丑数 Ugly Number I
2. 丑数 Ugly Number II
3. 丑数 Ugly Number III
4. 超级丑数 Super Ugly Number
🌟 每日一练刷题专栏 🌟
Golang每日一练 专栏
Python每日一练 专栏
C/C++每日一练 专栏
Java每日一练 专栏
1. 丑数 Ugly Number I
丑数 就是只包含质因数 2、3 和 5 的正整数。
给你一个整数 n ,请你判断 n 是否为 丑数 。如果是,返回 true ;否则,返回 false 。
示例 1:
输入:n = 6 输出:true 解释:6 = 2 × 3
示例 2:
输入:n = 1
输出:true
解释:1 没有质因数,因此它的全部质因数是 {2, 3, 5} 的空集。习惯上将其视作第一个丑数。
示例 3:
输入:n = 14 输出:false 解释:14 不是丑数,因为它包含了另外一个质因数 7 。
提示:
-2^31 <= n <= 2^31 - 1
代码:
class Solution:def isUgly(self, n: int) -> bool:if n <= 0:return Falsefor i in [2, 3, 5]:while n % i == 0:n //= ireturn n == 1# %%
s = Solution()
print(s.isUgly(6))
print(s.isUgly(1))
print(s.isUgly(14))for i in range(1,21):s = Solution()if s.isUgly(i):print(i, end=" ")
递归写法:
class Solution:def isUgly(self, n: int) -> bool:if n <= 0:return Falseelif n == 1:return Trueelif n % 2 == 0:return self.isUgly(n // 2)elif n % 3 == 0:return self.isUgly(n // 3)elif n % 5 == 0:return self.isUgly(n // 5)else:return False
# %%
s = Solution()
print(s.isUgly(6))
print(s.isUgly(1))
print(s.isUgly(14))for i in range(1,21):s = Solution()if s.isUgly(i):print(i, end=" ")输出:
True
True
False
1 2 3 4 5 6 8 9 10 12 15 16 18 20
2. 丑数 Ugly Number II
给你一个整数 n ,请你找出并返回第 n 个 丑数 。
丑数 就是只包含质因数 2、3 和/或 5 的正整数。
示例 1:
输入:n = 10 输出:12 解释:[1, 2, 3, 4, 5, 6, 8, 9, 10, 12] 是由前 10 个丑数组成的序列。
示例 2:
输入:n = 1 输出:1 解释:1 通常被视为丑数。
提示:
1 <= n <= 1690
代码:
class Solution:def nthUglyNumber(self, n: int) -> int:nums = [1]p_2, p_3, p_5 = 0, 0, 0for i in range(1, n):nums.append(min(nums[p_2]*2, nums[p_3]*3, nums[p_5]*5))if nums[-1] == nums[p_2]*2:p_2 += 1if nums[-1] == nums[p_3]*3:p_3 += 1if nums[-1] == nums[p_5]*5:p_5 += 1return nums[-1]# %%
s = Solution()
print(s.nthUglyNumber(10))
print(s.nthUglyNumber(1))for i in range(1,15):print(s.nthUglyNumber(i), end=" ")调用上题函数:
class Solution:def isUgly(self, n: int) -> bool:if n <= 0:return Falsefor i in [2, 3, 5]:while n % i == 0:n //= ireturn n == 1def nthUglyNumber(self, n: int) -> int:count = 0i = 1while count < n:if self.isUgly(i):count += 1if count == n:return ii += 1return -1# %%
s = Solution()
print(s.nthUglyNumber(10))
print(s.nthUglyNumber(1))for i in range(1,15):print(s.nthUglyNumber(i), end=" ")
输出:
12
1
1 2 3 4 5 6 8 9 10 12 15 16 18 20
3. 丑数 Ugly Number III
给你四个整数:n 、a 、b 、c ,请你设计一个算法来找出第 n 个丑数。
丑数是可以被 a 或 b 或 c 整除的 正整数 。
示例 1:
输入:n = 3, a = 2, b = 3, c = 5 输出:4 解释:丑数序列为 2, 3, 4, 5, 6, 8, 9, 10... 其中第 3 个是 4。
示例 2:
输入:n = 4, a = 2, b = 3, c = 4 输出:6 解释:丑数序列为 2, 3, 4, 6, 8, 9, 10, 12... 其中第 4 个是 6。
示例 3:
输入:n = 5, a = 2, b = 11, c = 13 输出:10 解释:丑数序列为 2, 4, 6, 8, 10, 11, 12, 13... 其中第 5 个是 10。
示例 4:
输入:n = 1000000000, a = 2, b = 217983653, c = 336916467 输出:1999999984
提示:
1 <= n, a, b, c <= 10^91 <= a * b * c <= 10^18- 本题结果在
[1, 2 * 10^9]的范围内
代码: 二分查找
class Solution:def nthUglyNumber(self, n: int, a: int, b: int, c: int) -> int:def gcd(x, y):return x if y == 0 else gcd(y, x % y)def lcm(x, y):return x // gcd(x, y) * yleft, right = 1, 2 * 10**9ab_lcm, ac_lcm, bc_lcm, abc_lcm = lcm(a, b), lcm(a, c), lcm(b, c), lcm(lcm(a, b), c)while left < right:mid = left + (right - left) // 2cnt = mid // a + mid // b + mid // c - mid // ab_lcm - mid // ac_lcm - mid // bc_lcm + mid // abc_lcmif cnt < n:left = mid + 1else:right = midreturn left# %%
s = Solution()
print(s.nthUglyNumber(n = 3, a = 2, b = 3, c = 5))
print(s.nthUglyNumber(n = 4, a = 2, b = 3, c = 4))
print(s.nthUglyNumber(n = 5, a = 2, b = 11, c = 13))print(s.nthUglyNumber(n = 1000000000, a = 2, b = 217983653, c = 336916467))
输出:
4
6
10
1999999984
4. 超级丑数 Super Ugly Number
超级丑数 是一个正整数,并满足其所有质因数都出现在质数数组 primes 中。
给你一个整数 n 和一个整数数组 primes ,返回第 n 个 超级丑数 。
题目数据保证第 n 个 超级丑数 在 32-bit 带符号整数范围内。
示例 1:
输入:n = 12, primes = [2,7,13,19]
输出:32
解释:给定长度为 4 的质数数组 primes = [2,7,13,19],前 12 个超级丑数序列为:[1,2,4,7,8,13,14,16,19,26,28,32] 。
示例 2:
输入:n = 1, primes = [2,3,5] 输出:1 解释:1 不含质因数,因此它的所有质因数都在质数数组 primes = [2,3,5] 中。
提示:
1 <= n <= 10^61 <= primes.length <= 1002 <= primes[i] <= 1000- 题目数据 保证
primes[i]是一个质数 primes中的所有值都 互不相同 ,且按 递增顺序 排列
代码:
from typing import List
class Solution:def nthSuperUglyNumber(self, n: int, primes: List[int]) -> int:dp = [1] * nk = len(primes)pointers = [0] * kfor i in range(1, n):choices = [dp[pointers[j]] * primes[j] for j in range(k)]dp[i] = min(choices)for j in range(k):if dp[pointers[j]] * primes[j] == dp[i]:pointers[j] += 1return dp[-1]# %%
s = Solution()
print(s.nthSuperUglyNumber(n = 12, primes = [2,7,13,19]))
print(s.nthSuperUglyNumber(n = 1, primes = [2,3,5]))
输出:
32
1
🌟 每日一练刷题专栏 🌟
✨ 持续,努力奋斗做强刷题搬运工!
👍 点赞,你的认可是我坚持的动力!
🌟 收藏,你的青睐是我努力的方向!
✎ 评论,你的意见是我进步的财富!
☸ 主页:https://hannyang.blog.csdn.net/
 | Golang每日一练 专栏 |
 | Python每日一练 专栏 |
 | C/C++每日一练 专栏 |
 | Java每日一练 专栏 |
相关文章:

Python每日一练(20230507) 丑数I\II\III、超级丑数
目录 1. 丑数 Ugly Number I 2. 丑数 Ugly Number II 3. 丑数 Ugly Number III 4. 超级丑数 Super Ugly Number 🌟 每日一练刷题专栏 🌟 Golang每日一练 专栏 Python每日一练 专栏 C/C每日一练 专栏 Java每日一练 专栏 1. 丑数 Ugly Number I …...

K8S常见异常事件与解决方案
集群相关 Coredns容器或local-dns容器重启 集群中的coredns组件发生重启(重新创建),一般是由于coredns组件压力较大导致oom,请检查业务是否异常,是否存在应用容器无法解析域名的异常。 如果是local-dns重启,说明local-dns的性能…...
测试5年从中兴 15K 跳槽去腾讯 32K+16,啃完这份笔记你也可以
粉丝小王转行做测试已经是第5个年头,一直是一个不温不火的小职员,本本分分做着自己的事情,觉得自己的工作已经遇到了瓶颈,一个偶然的机会,获得了一份软件测试全栈知识点学习笔记,通过几个月的学习ÿ…...

CentOS 临时IP与永久IP配置
CentOS 临时IP与永久IP配置 CentOS是一种广泛使用的Linux发行版,通常用于服务器和企业网络中。在安装和配置CentOS服务器时,必须为其配置IP地址以便访问。在本文中,我们将介绍如何在CentOS中配置临时IP地址和永久IP地址。 临时IP地址配置 临…...

集线器、网桥、交换机
一.集线器 集线器(HUB),它是工作在物理层的设备, 由于它只是工作在物理层的设备,所以它并不关心也不可能关心OSI上面几层所涉及的,它的工作机制流程是:从一个端口接收到数据包时,会在…...

api接口怎么用?
API接口是一种应用程序编程接口,它允许不同的软件应用程序之间进行通信和交互。通过使用API接口,开发人员可以轻松地将自己的应用程序集成到其他应用程序中,从而实现更丰富的功能和更好的用户体验。 API接口的使用方法一般包括以下几个步骤&a…...

Bad minute in crontab?
ERROR 详细 修改crontab出现如下错误: crontab: installing new crontab “/tmp/crontab.MswKCq”:0: bad minute errors in crontab file, can’t install. Do you want to retry the same edit? n crontab: edits left in /tmp/crontab.MswKCq 根因定位 通过…...
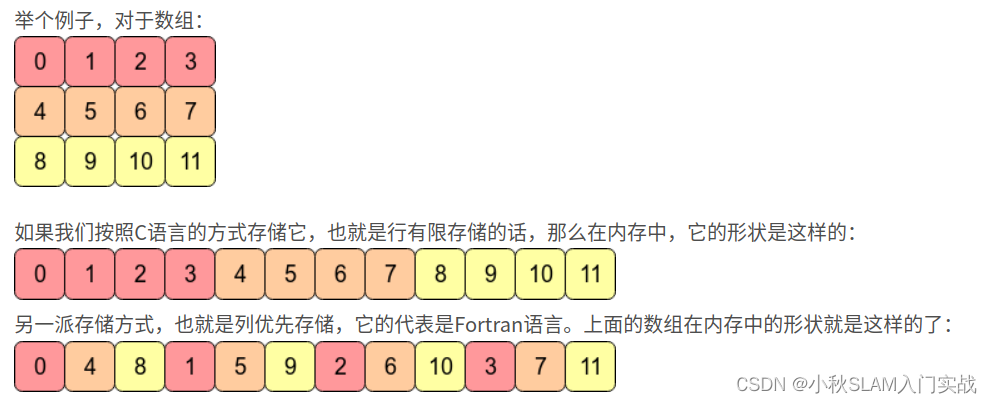
【二维矩阵如何存储在一维数组中(行优先和列优先)】
列优先和行优先的性能取决于具体的硬件架构和代码访问模式。在现代计算机中,内存访问的局部性(locality of reference)对性能至关重要。局部性分为两类:时间局部性(temporal locality)和空间局部性(spatial locality)。时间局部性表示最近访问过的数据项很可能在不久的…...
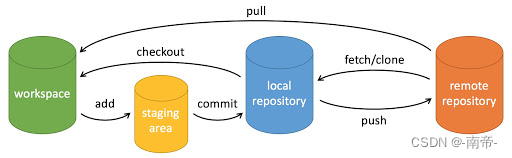
使用Gradle7.6+SpringBoot 3.0+java17创建微服务项目
系列文章目录 学习新版本,菜鸟一枚 会持续更新的 文章目录 系列文章目录前言一、搭建项目1.1、创建git仓库1.1.1、登录gitee,新建仓库1.1.2、得到如下命令(新建仓库使用创建git仓库 即可) 1.2、使用IDEA创建项目1.2.1、开发工具1.…...

pandas使用教程:apply函数、聚合函数agg和transform
文章目录 apply函数调用apply函数描述性统计apply函数lambda自定义 聚合函数aggregate/agg用字典实现聚合 transform函数多函数 Transform 重置索引与更换标签行重置索引行和列同时重置索引 apply函数调用 apply函数描述性统计 import numpy as np df.loc[:,Q1:Q4].apply(np.…...

使用rasterio裁剪遥感影像
文章目录 0. 数据准备1. polygon的坐标系转换1.1 polygon生成1.1.1 输入数据是shapefile1.1.2 输入数据是polygon 1.2 搞清楚遥感的坐标系和polygon的坐标系(重点)1.3 开始转换 2. 基于polygon的遥感影像裁剪2.1 基础裁剪方法2.1.1 使用rasterio保存2.1.2 使用numpy保存2.2 多线…...

BetaFlight统一硬件配置文件研读之set命令
BetaFlight统一硬件配置文件研读之set命令 1. 源由2. 代码分析3. 实例分析4. 配置情况4.1 set4.2 set parameter_name4.3 set parameter_name value 5. 参考资料 统一硬件配置文件的设计是一种非常好的设计模式,可以将硬件和软件的工作进行解耦。 1. 源由 cli命令…...

QT+OpenGL高级数据和高级GLSL
QTOpenGL高级数据和高级GLSL 本篇完整工程见gitee:QtOpenGL 对应点的tag,由turbolove提供技术支持,您可以关注博主或者私信博主 高级数据 OpenGL中的缓冲区 对象管理特定的GPU内存 在将缓冲区绑定到特定的缓冲区目标时候赋予它意义 OpenGL在内部会保…...
接口测试之Jmeter+Ant+Jenkins接口自动化测试平台
目录 平台简介 环境准备 Jenkins简介 下载与安装 平台搭建 依赖文件配置 build.xml配置 Ant构建 阿里大佬倾情演绎,3天让你学会Jmeter接口测试,学不会算我输_哔哩哔哩_bilibilihttps://www.bilibili.com/video/BV1Q84y1K7bK/?spm_id_from333.99…...
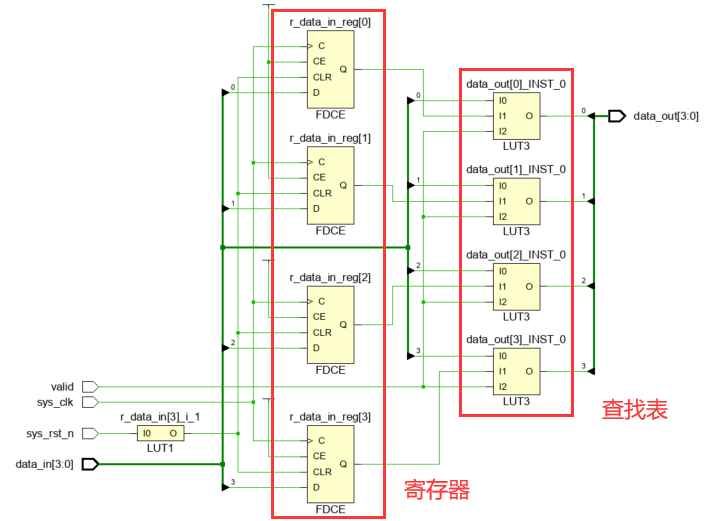
FPGA设计中锁存器产生、避免与消除
FPGA设计中锁存器产生、避免与消除 一、锁存器的产生1.1 组合逻辑中使用保持状态1.2 组合逻辑中的if-else语句或case语句未列出所有可能性1.3 小结 二、锁存器的避免三、锁存器的消除3.1 情况一 一、锁存器的产生 锁存器的产生主要有以下两种情况:(1&…...
一份标准的软件测试方案模板
第一章 概述 软件的错误是不可避免的,所以必须经过严格的测试。通过对本软件的测试,尽可能的发现软件中的错误,借以减少系统内部各模块的逻辑,功能上的缺陷和错误,保证每个单元能正确地实现其预期的功能。检测和排…...

【C++】-对于自定义类型的输入输出运算符重载
💖作者:小树苗渴望变成参天大树 ❤️🩹作者宣言:认真写好每一篇博客 💨作者gitee:gitee 💞作者专栏:C语言,数据结构初阶,Linux,C 文章目录 前言一、案例引入二、<<的重载三、>>的…...
js中什么是宏任务、微任务?宏任务、微任务有哪些?又是怎么执行的?)
(详解)js中什么是宏任务、微任务?宏任务、微任务有哪些?又是怎么执行的?
目录 参考资料 必看强烈建议十分钟看完视频 ,即可学会 必看参考详解宏任务微任务 笔记 宏任务与微任务 定时器的任务编排 promise的微任务处理逻辑 DOM渲染任务 任务队列共享内存 进度条的实现 任务拆分成多个任务 promise复杂任务分割 img算同步还是异步…...

Okta 即代码:云原生时代的身份管理
我们为什么应该将 Okta 配置作为代码进行管理? 对于需要跨多个应用程序和环境管理对其数字资源的访问的组织来说,Okta 可能是最受欢迎的选择,因为它提供了一系列使其在身份验证和授权方面很受欢迎的功能,例如: 单点登…...
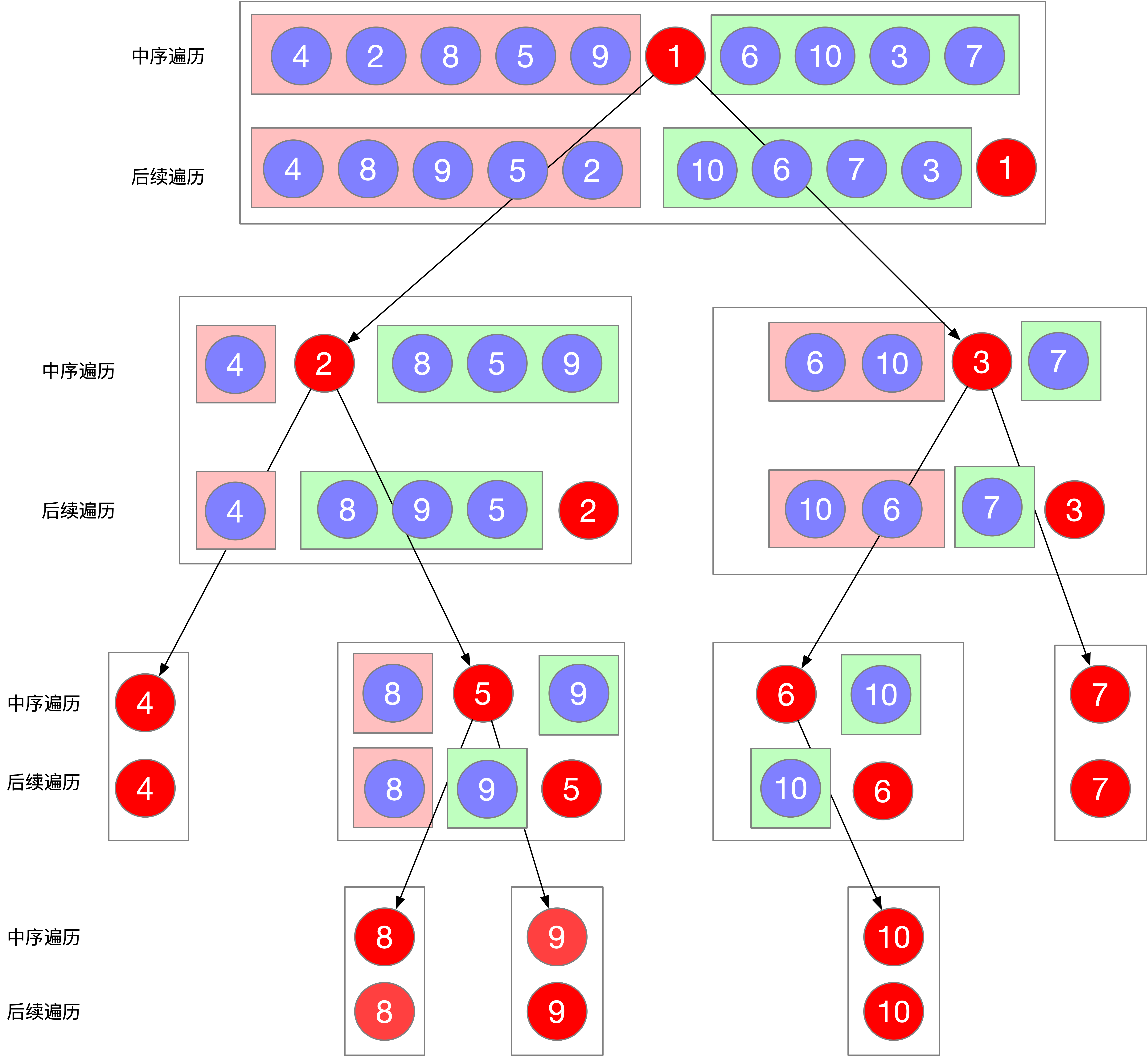
数据结构(六)—— 二叉树(7)构建二叉树
文章目录 如何使用递归构建二叉树1、创建一颗全新树(题1-5)2、在原有的树上新增东西(题6) 1 106 从 后序 与 中序 遍历序列构造二叉树2 105 从 前序 与 中序 遍历序列构造二叉树3 108 将有序数组转换为二叉搜索树(输入…...

龙虎榜——20250610
上证指数放量收阴线,个股多数下跌,盘中受消息影响大幅波动。 深证指数放量收阴线形成顶分型,指数短线有调整的需求,大概需要一两天。 2025年6月10日龙虎榜行业方向分析 1. 金融科技 代表标的:御银股份、雄帝科技 驱动…...

51c自动驾驶~合集58
我自己的原文哦~ https://blog.51cto.com/whaosoft/13967107 #CCA-Attention 全局池化局部保留,CCA-Attention为LLM长文本建模带来突破性进展 琶洲实验室、华南理工大学联合推出关键上下文感知注意力机制(CCA-Attention),…...

大型活动交通拥堵治理的视觉算法应用
大型活动下智慧交通的视觉分析应用 一、背景与挑战 大型活动(如演唱会、马拉松赛事、高考中考等)期间,城市交通面临瞬时人流车流激增、传统摄像头模糊、交通拥堵识别滞后等问题。以演唱会为例,暖城商圈曾因观众集中离场导致周边…...
)
IGP(Interior Gateway Protocol,内部网关协议)
IGP(Interior Gateway Protocol,内部网关协议) 是一种用于在一个自治系统(AS)内部传递路由信息的路由协议,主要用于在一个组织或机构的内部网络中决定数据包的最佳路径。与用于自治系统之间通信的 EGP&…...

基于Uniapp开发HarmonyOS 5.0旅游应用技术实践
一、技术选型背景 1.跨平台优势 Uniapp采用Vue.js框架,支持"一次开发,多端部署",可同步生成HarmonyOS、iOS、Android等多平台应用。 2.鸿蒙特性融合 HarmonyOS 5.0的分布式能力与原子化服务,为旅游应用带来…...

tree 树组件大数据卡顿问题优化
问题背景 项目中有用到树组件用来做文件目录,但是由于这个树组件的节点越来越多,导致页面在滚动这个树组件的时候浏览器就很容易卡死。这种问题基本上都是因为dom节点太多,导致的浏览器卡顿,这里很明显就需要用到虚拟列表的技术&…...

【Go语言基础【13】】函数、闭包、方法
文章目录 零、概述一、函数基础1、函数基础概念2、参数传递机制3、返回值特性3.1. 多返回值3.2. 命名返回值3.3. 错误处理 二、函数类型与高阶函数1. 函数类型定义2. 高阶函数(函数作为参数、返回值) 三、匿名函数与闭包1. 匿名函数(Lambda函…...

WebRTC从入门到实践 - 零基础教程
WebRTC从入门到实践 - 零基础教程 目录 WebRTC简介 基础概念 工作原理 开发环境搭建 基础实践 三个实战案例 常见问题解答 1. WebRTC简介 1.1 什么是WebRTC? WebRTC(Web Real-Time Communication)是一个支持网页浏览器进行实时语音…...

深度剖析 DeepSeek 开源模型部署与应用:策略、权衡与未来走向
在人工智能技术呈指数级发展的当下,大模型已然成为推动各行业变革的核心驱动力。DeepSeek 开源模型以其卓越的性能和灵活的开源特性,吸引了众多企业与开发者的目光。如何高效且合理地部署与运用 DeepSeek 模型,成为释放其巨大潜力的关键所在&…...

在Spring Boot中集成RabbitMQ的完整指南
前言 在现代微服务架构中,消息队列(Message Queue)是实现异步通信、解耦系统组件的重要工具。RabbitMQ 是一个流行的消息中间件,支持多种消息协议,具有高可靠性和可扩展性。 本博客将详细介绍如何在 Spring Boot 项目…...
