四元数快速入门【Quaternion】
四元数(Quaternion)是用于旋转和拉伸向量的数学运算符。 本文提供了一个概述,以帮助理解在空间导航等应用程序中对四元数的需求。

推荐:用 NSDT场景设计器 快速搭建3D场景。
可以通过多种方式在空间中准确定位、移动和旋转物体。 更熟悉和更容易可视化的滚动(Roll)、俯仰(Pitch)和偏航(Yaw)表示是有局限性的,在某些情况下应该用更强大的四元数代替。 随着对象的位置和方向发生变化,称为四元数的数学工具可用于旋转和缩放原始矢量。
三维空间中的物体可以定位在一个坐标系中,三个数从坐标系的原点延伸到空间中的一点,创建一个位置 r=(x,y,z) 向量。 如果对象的位置发生变化,向量将位于新的位置并且可能具有新的长度。 我们需要一种方法来测量或计算两个向量之间的变化。
1、Roll/Pitch/Yaw表示法的问题
大多数读者可能都知道,在空间中旋转的物体可以用它们沿三个轴的旋转角度来描述。 空间中的任何旋转都可以用这些旋转的组合来描述。
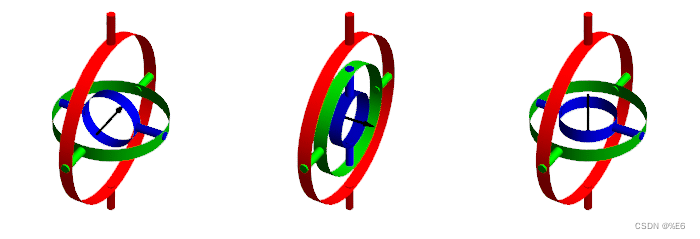
万向节提供偏航、滚动和俯仰运动。
旋转轴并不总是独立的,解也不总是唯一的。 两个万向节的平面可能会对齐,并且会发生称为万向节锁定(gimbal lock)的情况。 在万向节锁定中,三个万向节中的两个是平行或非常接近平行的,最初的三个自由度(偏航、俯仰和滚动)减少到两个自由度——两个旋转轴可以描述相同的旋转运动。 同时,失去了一个自由度,信息也消失了。 一旦发生万向节锁定,就不可能在没有外部参考的情况下重新定向轴。
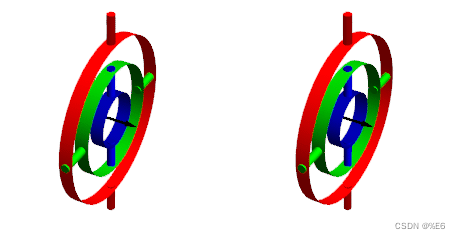
当绿色圆圈与红色圆圈对齐或接近对齐时发生万向节锁定
你可能还记得在有关阿波罗 13 号任务的电影中听到过万向节锁定这个词。 如果万向节锁定发生在爆炸之后,宇航员的惯性测量装置将无法追踪他们在天球中的位置,从而对他们本已绝望的处境产生负面影响。
现在来看看万向节锁背后的数学原理。
读者须知:为了保持在小型设备上的可读性,cos(x) 的所有实例都已替换为 Cx,sin(x) 的所有实例均已替换为 Sx。
围绕单个轴旋转一个矢量 r=(x,y,z) 需要一个旋转矩阵。 上图的三轴云台有三个轴对应三个旋转矩阵。
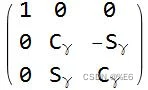
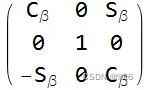

上面的三个矩阵分别表示:绕x 轴 旋转角度 γ,绕y 轴 旋转角度 β,绕z 轴旋转角度 α 。
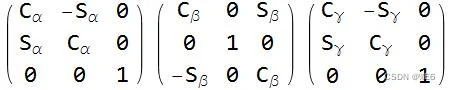
上面显示的是三个独立的 3×3 变换矩阵。 (围绕 z-y-z 旋转 α、β、γ 角度的变换)
从数学上讲,3×3 旋转矩阵是三个连续旋转的乘积。
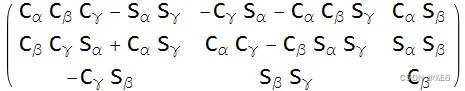
3×3 矩阵连续相乘时会产生一个 3×3 矩阵。 上面显示的是围绕 z-y-z 旋转角度 α、β、γ 。
存在多个转换矩阵,它们可以以各种顺序应用。 十二个旋转序列可以分为两类:
- 欧拉角:其中一个旋转轴重复(x-z-x,x-y-x,y-x-y,y-z-y,z-y-z,z-x-z)
- 泰特-布赖恩角,围绕所有轴(x-z-y, x-y-z、y-x-z、y-z-x、z-y-x、z-x-y)旋转
我任意选择了 z-y-x 变换矩阵来处理下面的示例。
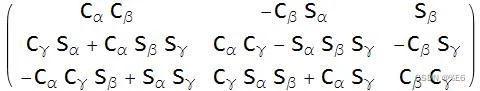
上图是围绕α、β、γ旋转z-y-x的变换矩阵。
当使用 β =π/2 代入 z-y-x 变换矩阵时,万向节锁在我们的示例矩阵中在数学上变得明显(其他变换矩阵在不同条件下失败)。随着角度 β →π /2 以及 sin(β)→0 ,您可以在下面看到对矩阵的简化效果。
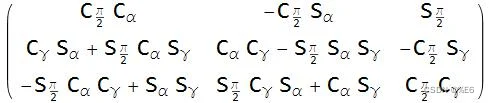
上面的矩阵中将π /2 带入β ,得到
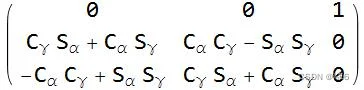
可以看到,当 β 接近 π/2 时, cos(π/2) 导致矩阵中的几项变为零。
另一种看待问题的方法是采用原始变换矩阵(我再次选择 z-y-x)并使用三角恒等式将三角函数内的变量聚集在一起。 注意角度的初始相互依赖性。
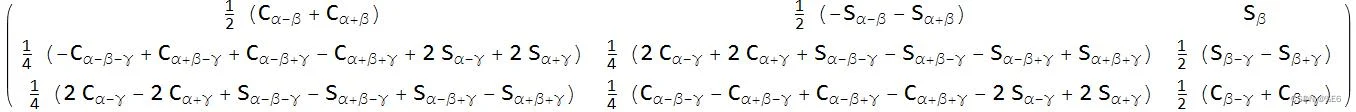
替换后,角度之间唯一存在的关系是 α + γ 。
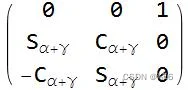
通过固定 β = π/2 ,我们已经消除了 α−γ 的所有情况,牺牲一定程度的自由度。
虽然很容易想象滚动、俯仰和偏航,但如果你正在设计一个能够自由指向空间中任何方向的系统,最终会遇到万向节锁定。
2、四元数
威廉·汉密尔顿于 1843 年发明了四元数,作为一种允许他对向量进行乘法和除法、旋转和拉伸的方法。
我在下面提出的内容旨在说明,但绝不是数学上严格的。 它应该足以让你在计算机科学和工程环境的入门级理解四元数。 对于数学课来说,这并不意味着就足够了。 如果你需要更深入的信息,加利福尼亚州立大学富勒顿分校物理学和数学教授 Alfonso Agnew 博士推荐了以下有关该主题的书籍:
- 四元数和旋转序列:在轨道、航空航天和虚拟现实中的应用入门 (Kupiers)
- Clifford 代数和旋量 (Lounesto)
- 可视化四元数 (Hanson)
汉密尔顿的发现是,虽然没有明显的方法可以将两组三个数字相乘并除以得到三个数字(可能代表坐标的向量),但可以将两组四个数字相乘并相除并得到四个 数字。 四元数是两组四个数的商,由一个标量和一个向量组成。
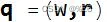
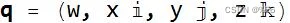
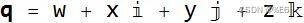
其中,
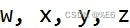
为实数,且
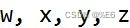
为四元数单位。
任意两点之间的方向可以用三个数表示,这三个数分别位于 (-1,1) 范围内,其总大小为 (-1 ≤ x ≤1, -1 ≤ y ≤ 1, -1 ≤ z ≤ 1)并且 √x2+y2+z^2 = 1 。这四个数字一起创建了一个描述旋转和距离的四元数。
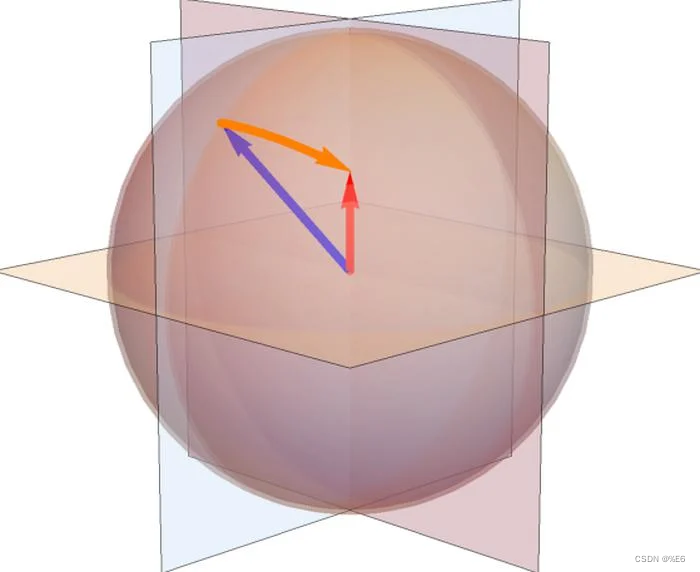
四元数提供旋转向量所需的信息,只需四个数字而不是旋转矩阵所需的九个数字。
如果你熟悉数学和矩阵符号,请跳至下面的四元数数学,并跳过接下来两节中复数和矩阵数学的复习。
3、复数
参见 AAC 教科书第 2 卷 — 第 2 章。
发明复数是为了解决没有实数解的问题。 在发明 √-1 之前 , x^2 = -1这类问题始终无解。 复数可以想象成位于一个平面上,数的实部沿水平轴表示,数的虚部沿垂直轴表示。 在笛卡尔坐标中,它们通常以类似于 x+yi 或 (x,y) 的形式表示。 两个复数可以相加、相减、相乘和相除。
相加:
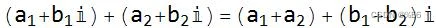
相减:
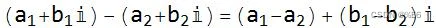
相乘:
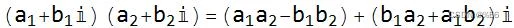
相除:
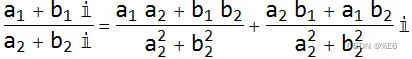
无缩放旋转:
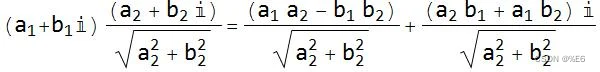
一个例子是 2+3i 逆时针旋转π/2 可以通过与 0+i 相乘得到:
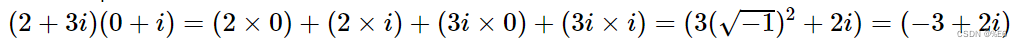
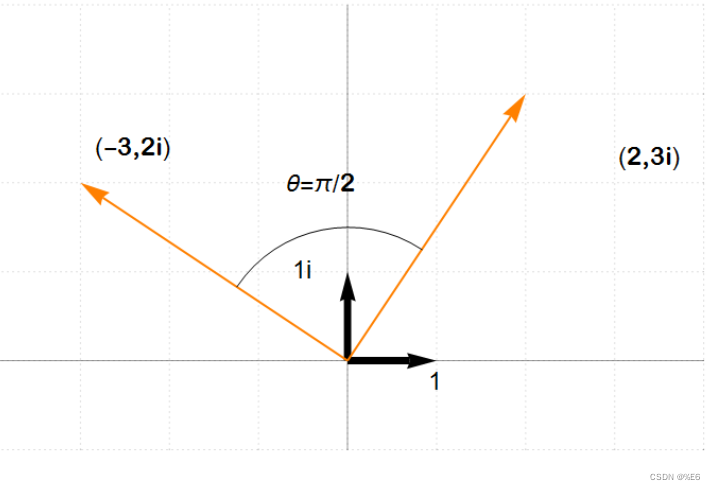
欧拉开发了一种在复数极平面中旋转复数的方法,汉密尔顿以此为基础建立了他的想法。
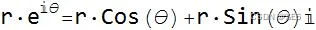
虽然这远非对复数主题的完整处理,但它通过以下方式为四元数提供了一个垫脚石:
- 复数可以很容易地进行加、减、乘和除,而无需使用三角函数(尽管复数可以用极坐标形式表示或从极坐标形式分别用 cos 和 sin 分解为实部和虚部)。
- 将复数乘以虚数单位“i”产生四分之一圈。 与四元数类似,将任意两个四元数单位相乘将导致围绕垂直于两个初始轴的轴旋转。
4、矩阵数学
- 标量
标量是表示沿公共比例尺或轴的位置的数字。 标量变量没有应用于它们的特殊格式。
- 向量
向量是一个有序数字的列表,描述了在特定方向上沿尺度的位置。 它被可视化为具有长度和方向的直线。 本文中矢量变量以粗体 r 显示,偶尔会使用上标箭头。 向量可以有两个或更多元素。
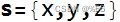
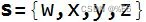
多个向量通过不同的变量名或下标来区分。
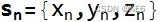
或者
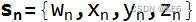
- 叉积
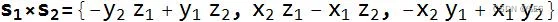
- 点积
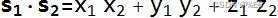
- 长度
矢量的长度是从起点到终点的直线距离。 在数学上,它是单个元素平方和的平方根。
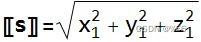
- 矩阵
矩阵是单个元素的数组,可以乘以向量以对其进行转换。 矩阵可以平移、旋转和缩放向量。 下面显示的是一个通用的 3×3 矩阵

- 矩阵应用于向量
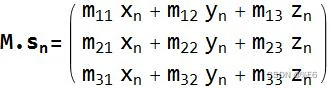
- 旋转矩阵
旋转矩阵可以改变向量指向的方向,在空间中重新定向它们。 以下矩阵围绕笛卡尔轴旋转向量而不缩放它们。
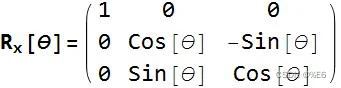
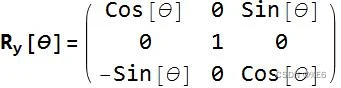
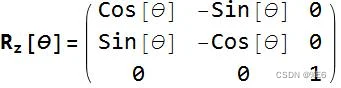
- 矩阵A与B相乘
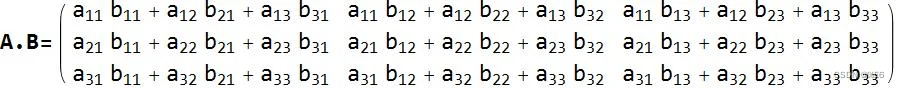
本节简要回顾向量和矩阵数学,并与下面的四元数规则进行对比。
5、四元数
如前所述,四元数由一个标量和一个向量组成。
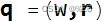
由于标量和向量都存在于四元数中,因此用于处理它们的数学规则是标量和向量数学的组合。
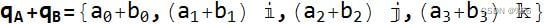
- (非交换)四元数乘法
两个四元数相乘的结果是一个新的四元数。

- 四元数内积
四元数内积是两个四元数对应的实系数相乘得到的标量。
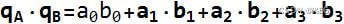
- 四元数共轭(Conjugate)
每个四元数都有一个相反数,可以通过仅对四元数的向量部分的系数求反来找到。
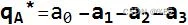
- 四元数范数(Norm)
四元数通常应始终位于单位球面上。 范数应等于 1。如果你的四元数偏离单位球体,可以将四元数的每个元素除以范数以返回单位球体。
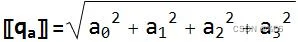
- 四元数转旋转矩阵
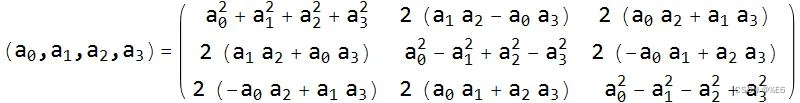
6、结束语
四元数是使用一组有序的四个数字来描述 3D 空间中的方向或旋转的另一种方法。 它们能够唯一地描述围绕任意轴的任何三维旋转,并且不会受到万向节锁定的影响。 如果你的应用程序中的传感器或物体能够在 3D 空间中的任何位置移动,那么它们在跟踪物体方面优于欧拉角。
原文链接:四元数快速指南 - BimAnt
相关文章:
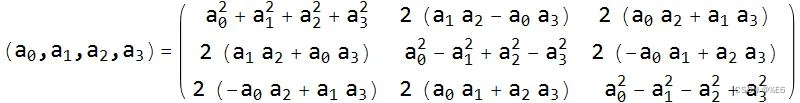
四元数快速入门【Quaternion】
四元数(Quaternion)是用于旋转和拉伸向量的数学运算符。 本文提供了一个概述,以帮助理解在空间导航等应用程序中对四元数的需求。 推荐:用 NSDT场景设计器 快速搭建3D场景。 可以通过多种方式在空间中准确定位、移动和旋转物体。 …...
为什么我们要使用向量化运算
问题背景 如果你是matlab用户,你一般都会使用向量化运算进行编程。原因也许很简单,因为matlab针对向量化运算在底层做了深度优化,尤其是针对矩阵乘法调用了MKL之类的高度优化的第三库来加速。所以我们在推演算法的阶段,尽量的以向…...
Makefile零基础教学(一)初识makefile
从这篇文章开始就开始进入 Makefile 的零基础教程,相信只要看了本教程的都可以对 Makefile 有一个清晰的理解和正确的运用。那么现在就开始我们的 Makefile 学习之路。 文章目录 一、什么是 Makefile,优点?二、什么是 make, 为什么使用make?…...

如何使用SpringMVC之常用注解
❣️关注专栏:JavaEE Spring MVC ⌛️ 1. Spring MVC 创建和连接⌛️ 1.1 RequestMapping⌛️ 1.2 GetMapping⌛️ 1.3 PostMapping ⌛️ 2. 获取参数⌛️ 2.1 传递/获取单个参数⌛️ 2.2 传递/获取多个参数⌛️ 2.3 传递/获取对象⌛️ 2.4 参数重命名⌛️ 2.4.1 …...

Vue3的axios请求封装,请求拦截,相应拦截
对于三者放在Service.js中封装,方便使用 axios.create 的作用是创建一个新的 axios 实例,该实例可以具有自定义配置。通过使用 axios.create,您可以为任何 API 生成一个客户端,并在使用同一客户端的任何调用中重复使用相同的配置…...
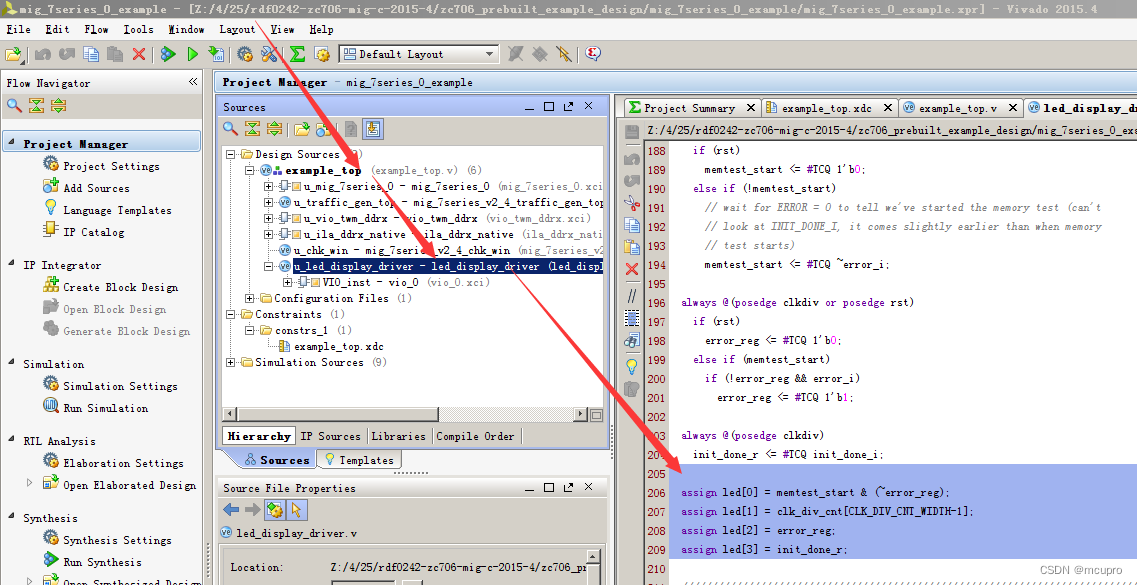
ZC706P试验PL_DDR3内存条的步骤方法
ZC706P 板卡完全兼容XILINX官方的ZC706,当然也支持PL外挂的1G的DDR3内存条,这个片BLOG我提供从官方下载的一个文档和一个项目,演示一下验证DDR3的步骤。 步骤1:准备好板子,安装好软件。 链接:https://pan.baidu.com/s…...
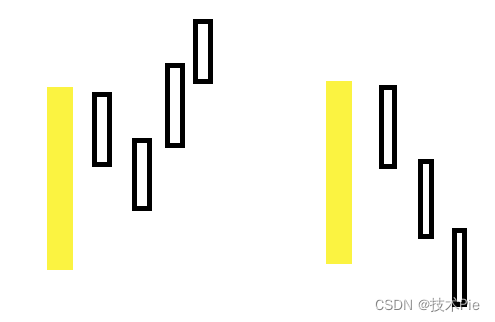
通达信W底形态选股公式,也称双底形态
W底形态,也称双底形态,是一种经典的技术分析形态,代表了跌势的逆转。看起来像字母 "W",描述了一波下跌,反弹,再次下跌到与上一波下跌相同或相近的位置,最后是另一波反弹。W底形态两次…...

java语言与算法、数据结构的用法
Java语言是一种广泛使用的计算机编程语言,也是开发各种软件和操作系统的重要工具之一。除了具有高效性和可移植性之外,Java语言还具有丰富的算法和数据结构支持,可以帮助程序员轻松地解决各种问题。 算法和数据结构是计算机科学中的两个基本…...

中国社科院与美国杜兰大学金融管理硕士项目,引领你走在金融行业前沿
作为金融领域从业人员时刻都在关注行业最新资讯,只有掌握一手的前沿讯息,才能在职场上无往不胜。针对在职的你,如何利用业余时间让自己更增值呢,中国社科院与美国杜兰大学金融管理硕士项目引领你走在金融行业前沿。 金融管理硕士…...
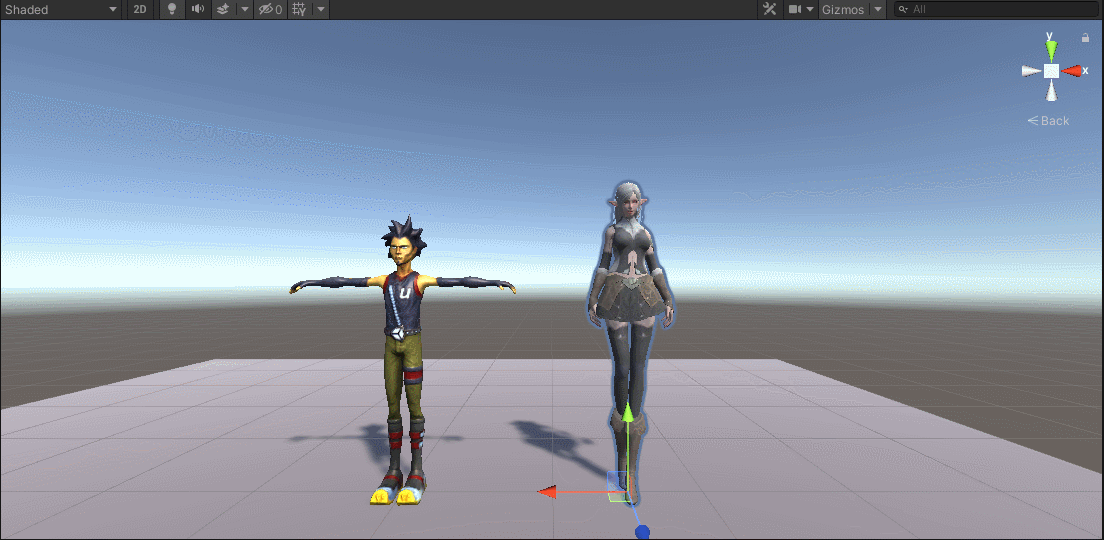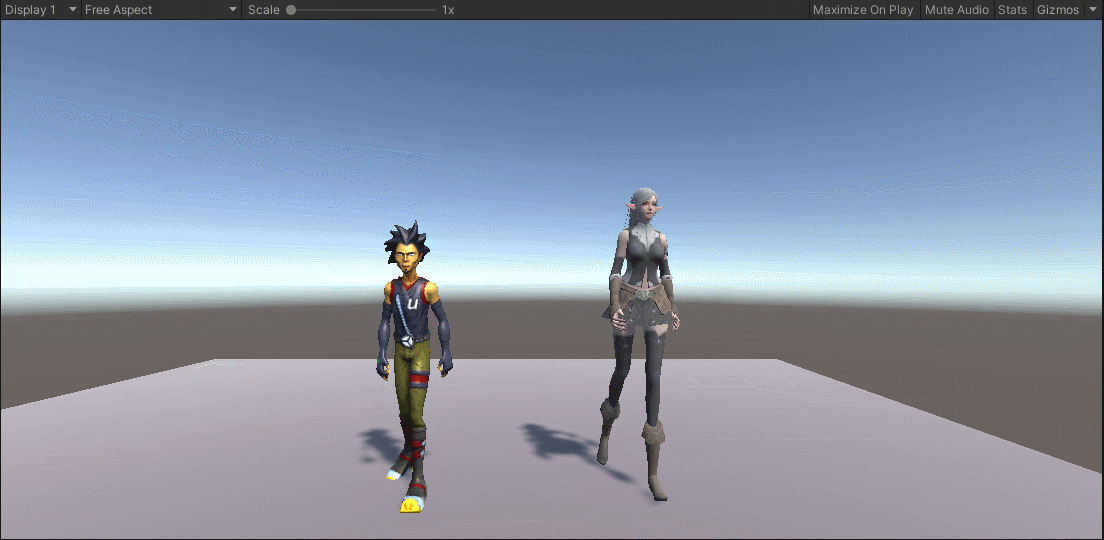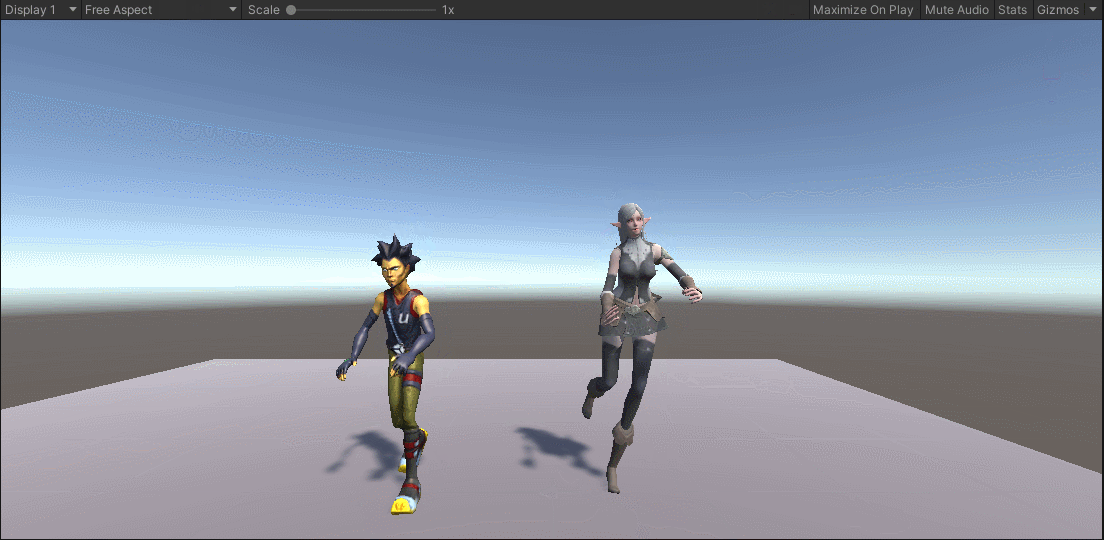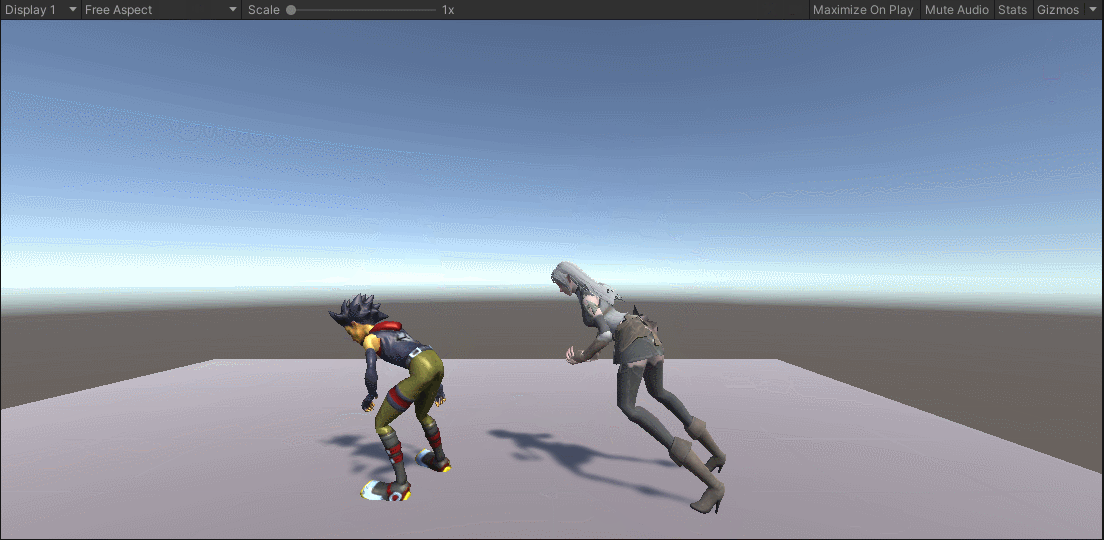
第三十五章 Unity人形动画(下)
本章内容主要就是动画数据的独立文件使用方式。有了独立的动画文件,我们就可以将其应用到其他模型上面了。最简单的方式就是,我们可以给其他模型编辑动画控制器的时候,使用这些动画文件。Unity则给我们提供了更加高级的共享方式,就…...
)
vue导入导出excel、设置单元格背景色、文字居中、合并单元格、设置列宽(使用xlsx库和xlsx-style库)
xlsx xlsx是由SheetJS开发的一个处理excel文件的npm库 适用于前端开发者实现导入导出excel文件的经典需求 为了区别于xlsx文件,突出其应用语言,该库通常又被称为js-xlsx 导出js数据为Excel文件 需要以下步骤: 安装 xlsx 库 你可以使用 …...

java 线程池
线程池 是 一个 容器,其中管理着多个线程(预先创建并维护一定数量的线程),当有一个任务a需要一个线程去完成时,从容器(线程池)中获取一个线程A去执行任务a,当线程A完成任务a后,线程A…...

音频焦点使用及原理
音频焦点使用及原理 本博客代码基于Android 10源码 为什么会有音频焦点这一概念? 在Android音频领域中,应用层所有的App播放音频,最终都是走到音频回播线程PlaybackThread中,如果多个App都走到同一个PlaybackThread中去࿰…...

PyQt5桌面应用开发(8):从QInputDialog转进到函数参数传递
本文目录 PyQt5桌面应用系列How old are you, Dialog?QInputDialog minimalistwhy not lambdaand how partial worksSummary PyQt5桌面应用系列 PyQt5桌面应用开发(1):需求分析 PyQt5桌面应用开发(2):事件…...

2.0 Vue框架设计的核心要素
本章主要讲解,一个好的框架在构建的时候,需要考虑到的要素,包含报错信息反馈、警告信息反馈、减少打包体积、良好的输出、特性开关(兼容)等 1、提升用户开发体验 提升用户开发体验主要体现在用户使用框架进行开发时&…...

“智慧赋能 强链塑链”——精细化工行业仓储物流数字化转型探讨
精细化工行业作为衡量国家化学工业水平高低的重要标志,为国民经济提供重要的终端产品支持,相比较大化工产品,精细化工产品需要高度专业技能和工艺,其生产过程需要复杂的化学反应,以及严格的控制条件,产出的…...
用DG备库做的rman备份恢复一个数据库
环境描述: 1.因为主库存储空间不足,于是将备份放在dg备库上做。 2.主库因为磁盘空间问题,数据文件有两个目录。 3.dg备库因为主库两个数据文件目录里面有两个同名数据文件,所有dg备库也有两个数据文件目录。 4.主库与备库与测…...

JAVA中的IO操作有哪些?
在Java编程语言中,输入/输出(IO)操作是很重要的部分,它允许程序从外部系统读取数据,或将数据输出到外部系统。Java提供了一组强大的IO类库,可以让开发人员方便地进行各种IO操作。 Java中的IO操作可以分为两…...
10:00面试,10:04就出来了 ,问的实在是太...
从外包出来,没想到竟然死在了另一家厂子 自从加入这家公司,每天都在加班,钱倒是给的不少,所以我也就忍了。没想到12月一纸通知,所有人都不许加班,薪资直降30%,顿时有吃不起饭的赶脚。 好在有个…...
wangzherongyao PMO
感谢【五一节】大家的相遇,总结下。 2023年05月02日,【第一组】组队开黑 我总结了下这天为什么打的那么好,首先赛季初段位在王者附近,大家心态重视程度也高,不轻敌,也不盲目,运营好兵线一步一步…...

国防科技大学计算机基础课程笔记02信息编码
1.机内码和国标码 国标码就是我们非常熟悉的这个GB2312,但是因为都是16进制,因此这个了16进制的数据既可以翻译成为这个机器码,也可以翻译成为这个国标码,所以这个时候很容易会出现这个歧义的情况; 因此,我们的这个国…...

练习(含atoi的模拟实现,自定义类型等练习)
一、结构体大小的计算及位段 (结构体大小计算及位段 详解请看:自定义类型:结构体进阶-CSDN博客) 1.在32位系统环境,编译选项为4字节对齐,那么sizeof(A)和sizeof(B)是多少? #pragma pack(4)st…...

python/java环境配置
环境变量放一起 python: 1.首先下载Python Python下载地址:Download Python | Python.org downloads ---windows -- 64 2.安装Python 下面两个,然后自定义,全选 可以把前4个选上 3.环境配置 1)搜高级系统设置 2…...

OkHttp 中实现断点续传 demo
在 OkHttp 中实现断点续传主要通过以下步骤完成,核心是利用 HTTP 协议的 Range 请求头指定下载范围: 实现原理 Range 请求头:向服务器请求文件的特定字节范围(如 Range: bytes1024-) 本地文件记录:保存已…...

Linux --进程控制
本文从以下五个方面来初步认识进程控制: 目录 进程创建 进程终止 进程等待 进程替换 模拟实现一个微型shell 进程创建 在Linux系统中我们可以在一个进程使用系统调用fork()来创建子进程,创建出来的进程就是子进程,原来的进程为父进程。…...

jmeter聚合报告中参数详解
sample、average、min、max、90%line、95%line,99%line、Error错误率、吞吐量Thoughput、KB/sec每秒传输的数据量 sample(样本数) 表示测试中发送的请求数量,即测试执行了多少次请求。 单位,以个或者次数表示。 示例:…...

客户案例 | 短视频点播企业海外视频加速与成本优化:MediaPackage+Cloudfront 技术重构实践
01技术背景与业务挑战 某短视频点播企业深耕国内用户市场,但其后台应用系统部署于东南亚印尼 IDC 机房。 随着业务规模扩大,传统架构已较难满足当前企业发展的需求,企业面临着三重挑战: ① 业务:国内用户访问海外服…...

命令行关闭Windows防火墙
命令行关闭Windows防火墙 引言一、防火墙:被低估的"智能安检员"二、优先尝试!90%问题无需关闭防火墙方案1:程序白名单(解决软件误拦截)方案2:开放特定端口(解决网游/开发端口不通)三、命令行极速关闭方案方法一:PowerShell(推荐Win10/11)方法二:CMD命令…...

验证redis数据结构
一、功能验证 1.验证redis的数据结构(如字符串、列表、哈希、集合、有序集合等)是否按照预期工作。 2、常见的数据结构验证方法: ①字符串(string) 测试基本操作 set、get、incr、decr 验证字符串的长度和内容是否正…...

【多线程初阶】单例模式 指令重排序问题
文章目录 1.单例模式1)饿汉模式2)懒汉模式①.单线程版本②.多线程版本 2.分析单例模式里的线程安全问题1)饿汉模式2)懒汉模式懒汉模式是如何出现线程安全问题的 3.解决问题进一步优化加锁导致的执行效率优化预防内存可见性问题 4.解决指令重排序问题 1.单例模式 单例模式确保某…...
