【CS224W】(task4)图嵌入表示学习
note
- node2vec:
- 计算随机游走概率
- 从节点uuu开始模拟rrr条长度为lll的游走链路
- 使用 Stochastic Gradient Descent 优化损失函数
- Node2vec在节点分类方面表现更好;而其他方法在链路预测上效果更好,如random walk效率更高;
- graph embeddings:
- 方法1:对应子图or图的节点embedding进行sum或avg计算;
- 方法2:创建横跨子图的super-node
- deepwalk等价于对以下表达式进行矩阵分解:log(vol(G)(1T∑r=1T(D−1A)r)D−1)−logb\log \left(\operatorname{vol}(G)\left(\frac{1}{T} \sum_{r=1}^T\left(D^{-1} A\right)^r\right) D^{-1}\right)-\log b log(vol(G)(T1r=1∑T(D−1A)r)D−1)−logb

文章目录
- note
- 一、Node embedding: Encoder + Decoder
- 1.1 embedding-lookup
- 1.2 节点相似的定义
- 1.3 unsupervised/self-supervised
- 二、Random Walk
- 2.1 notation
- 2.2 Algorithm:DeepWalk
- (1)SkipGram
- (2)Hierarchical Softmax
- (3)Optimization
- 2.3 代码实战
- 2.4 小结
- 三、在同质性和结构性间权衡:Node2vec
- 3.1 同质性和结构性
- 3.2 如何表达结构性和同质性
- 3.3 实验证实+代码例子
- 四、Embedding Entire Graphs
- 4.1 得到子图或整图的embedding
- 4.2 anonymous walks的应用
- 4.3 小结
- 附:思考题
- 附:时间安排
- Reference
一、Node embedding: Encoder + Decoder
本讲是图表示学习综述,介绍了图嵌入(节点嵌入)表示学习的基本框架和编码器-解码器架构,将节点嵌入映射为低维、连续、稠密向量。向量空间的相似度反映了对应节点在原图上的相似度。在同一个随机游走序列中共同出现的节点,视为相似节点,从而构建类似Word2Vec的自监督学习场景。衍生出DeepWalk、Node2Vec等基于随机游走的图嵌入方法。
从数学上,随机游走方法和矩阵分解是等价的。
进而讨论嵌入整张图的方法,可以通过所有节点嵌入向量聚合、引入虚拟节点、匿名随机游走等方法实现。

- embedding编码网络中的信息,可用于下游任务, 图表示学习使得省去特征工程。

- 图GGG,节点集VVV,邻接矩阵AAA(二维,这里化简,不考虑节点的特征等信息)
- node embedding:将节点信息编码为space中的embedding,使得embedding的相似度计算(如cos点积计算等)近似于节点之间真实的相似度

1.1 embedding-lookup
- 注意两点:

- shallow encoding:encoder仅为embedding-lookup表ENC(v)=zv=Z⋅v\operatorname{ENC}(v)=\mathbf{z}_v=\mathbf{Z} \cdot v ENC(v)=zv=Z⋅v
- Z∈Rd×∣V∣\mathbf{Z} \in \mathbb{R}^{d \times|\mathcal{V}|}Z∈Rd×∣V∣矩阵中,每列是对应的节点的embedding
- v∈I∣V∣v \in \mathbb{I}^{|\mathcal{V}|}v∈I∣V∣ 是单位矩阵
- 方法:deepwalk、node2vec等
- goal:对于相似节点(u, v),优化参数,使得similarity(u,v)≈zvTzu\operatorname{similarity}(u, v) \approx \mathbf{z}_v^{\mathrm{T}} \mathbf{z}_u similarity(u,v)≈zvTzu
1.2 节点相似的定义
- 有边
- 共享邻居
- 有相似的structural roles
- 随机游走random walk定义的节点相似度
1.3 unsupervised/self-supervised
无监督or自监督学习:不使用节点的标签和特征,直接得到节点的度量(如embedding)
二、Random Walk
2.1 notation
- zu\mathbf{z}_uzu:我们想学习到的节点u embedding
- P(v∣zu)P\left(v \mid \mathbf{z}_u\right)P(v∣zu)条件概率:已知节点u embedding,基于random walk的要访问节点v的概率
- 通过非线性函数得到预测概率:
- softmax函数将数据归一化为和为1的结果:σ(z)[i]=ez[i]∑j=1Kez[j]\sigma(\mathbf{z})[i]=\frac{e^{z[i]}}{\sum_{j=1}^K e^{z[j]}}σ(z)[i]=∑j=1Kez[j]ez[i]
- sigmoid函数:转为(0, 1)范围内,公式为S(x)=11+e−xS(x)=\frac{1}{1+e^{-x}}S(x)=1+e−x1
2.2 Algorithm:DeepWalk

算法由两部分组成:
- (1)随机游走序列生成器;
- (2)向量更新。
随机游走:对图G均匀地随机采样一个节点viv_ivi,并作为random walk的根结点WviW_{v_{i}}Wvi,然后一直向周围邻居采样,直到达到最大路径长度ttt。
随机游走的长度没有限制,但是在实验中设置最大步长是固定的。

- 输出:一个顶点表示矩阵Φ\PhiΦ,大小为∣V∣×d|V|\times d∣V∣×d
- 第二行:构建Hierarchical Softmax
- 第三行:对每个节点做γ\gammaγ次随机游走
- 第四行:打乱网络中的节点
- 第五行:以每个节点为根结点生成长度为ttt的随机游走
- 第七行:根据生成的随机游走使用skip-gram模型利用梯度的方法对参数进行更新。
其中SkipGram参数更新的细节如下:

(1)SkipGram
SkipGram参数更新的细节如下:

SkipGram算法是语言模型中,最大化窗口www中出现的词的概率的方法(梯度下降),外层for循环是对这个序列中的每个词进行操作,内层for循环是对每个词的窗口大小为www的词序列进行操作。具体操作是用一个似然函数J(Φ)J(\Phi)J(Φ)表示Φ\PhiΦ,通过梯度下降(对J(Φ)J(\Phi)J(Φ)求导)更新参数(α\alphaα是学习速率)。
从词向量学习的角度看,基于神经网络语言模型的预训练方法存在缺点:当对t时刻词进行预测时,模型只利用了历史词序列作为输入,而损失了与“未来”上下文之间的共现信息。于是大佬们提出更强的词向量预训练模型Word2Vec,其中包括CBOW(Continuous Bag-of-Words)模型以及Skip-gram模型。
(2)Hierarchical Softmax
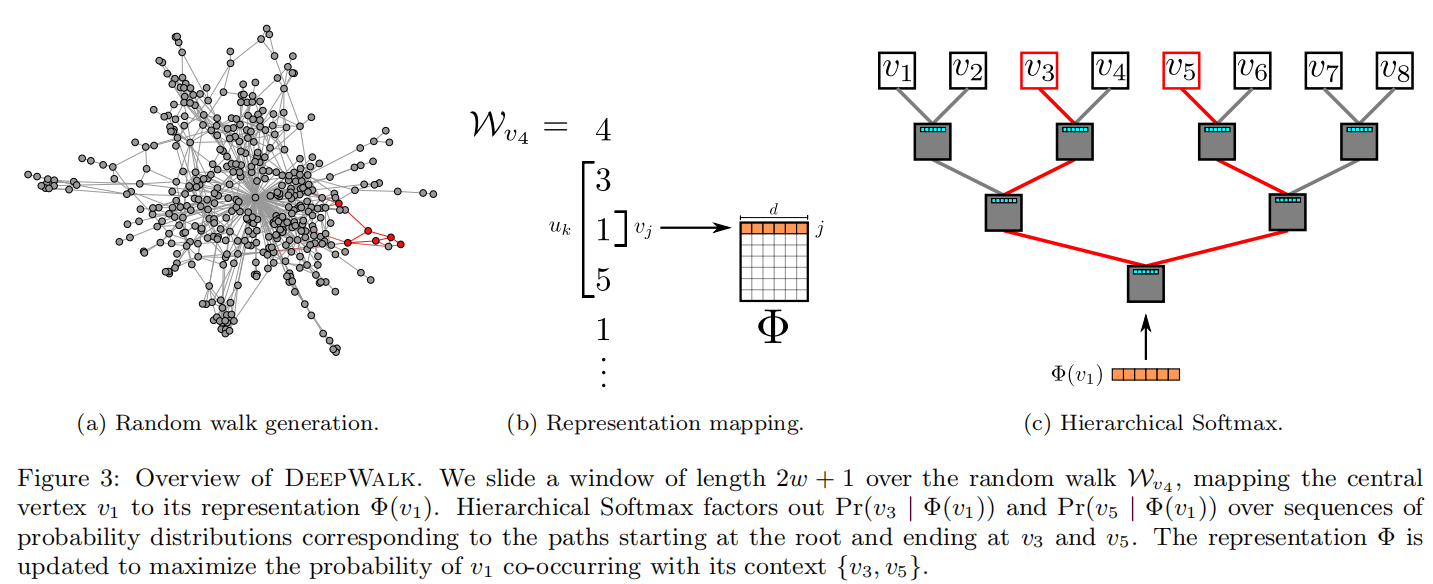
在计算 Pr(uk∣Φ(vi))\Pr(u_k|\Phi(v_i))Pr(uk∣Φ(vi)) 时,可以利用Hierarchical Softmax二叉树[29, 30]加速。作者将所有节点作为二叉树的叶子节点,就可以用从根节点到叶子节点的路径来表示每个节点。二叉树若有∣V∣|V|∣V∣个叶子节点,则深度至多为log∣V∣\log|V|log∣V∣。这样就会有:
Pr(uk∣Φ(vj))=∏l=1⌈log∣V∣⌉Pr(bl∣Φ(vj))\Pr(u_k|\Phi(v_j))=\prod_{l=1}^{\lceil\log|V|\rceil}\Pr(b_l|\Phi(v_j)) Pr(uk∣Φ(vj))=l=1∏⌈log∣V∣⌉Pr(bl∣Φ(vj))其中b0,b1,...,b⌈log∣V∣⌉b_0, b_1, ..., b_{\lceil\log|V|\rceil}b0,b1,...,b⌈log∣V∣⌉是一系列二叉树中的非叶子节点。这样就可以用较少的分类器完成这个任务,将计算复杂度由O(∣V∣)O(|V|)O(∣V∣)降低至O(log∣V∣)O(\log|V|)O(log∣V∣)。
更进一步,还可以结合节点出现频率,使用霍夫曼编码,为更频繁出现的节点分配稍短的路径,再次降低计算复杂度。
(3)Optimization
模型参数集是{Φ,T}\{\Phi, T\}{Φ,T},使用随机梯度下降算法 SGDSGDSGD(一次训练一个样本)进行优化参数。通过方向传播计算损失函数关于参数的偏导数,SGD的学习率初始设置为2.5%,然后随着训练过程中看到的顶点数量的增加而线性减少。
- 目标:使对每个节点 u,NR(u)u, N_R(u)u,NR(u) 的节点和 zuz_uzu 靠近, 即 P(NR(u)∣zu)P\left(N_R(u) \mid z_u\right)P(NR(u)∣zu) 值大。
- f:u→Rd:f(u)=zu\mathrm{f}: \mathrm{u} \rightarrow \mathbb{R}^{\mathrm{d}}: \mathrm{f}(\mathrm{u})=\mathbf{z}_{\mathrm{u}}f:u→Rd:f(u)=zu。
- 优化embedding的log-likelihood目标函数:
maxf∑u∈VlogP(NR(u)∣zu)\max _f \sum_{u \in V} \log \mathrm{P}\left(N_{\mathrm{R}}(u) \mid \mathbf{z}_u\right) fmaxu∈V∑logP(NR(u)∣zu)

【负采样优化】
但是由于求解上面目标函数的时间复杂度很高,需要O(∣V∣2)\mathrm{O}\left(|\mathrm{V}|^2\right)O(∣V∣2),可以通过负采样优化该公式的分母,即不用所有节点作为归一化的负样本。

2.3 代码实战
# DiGraph with 100 nodes and 4961 edges
import networkx as nx
import numpy as np
from tqdm import tqdm
from gensim.models import word2vecdef walkOneTime(g, start_node, walk_length):walk = [str(start_node)] # 初始化游走序列for _ in range(walk_length): # 最大长度范围内进行采样current_node = int(walk[-1])successors = list(g.successors(current_node)) # graph.successor: 获取当前节点的后继邻居if len(successors) > 0:next_node = np.random.choice(successors, 1)walk.extend([str(n) for n in next_node])else:breakreturn walkdef getDeepwalkSeqs(g, walk_length, num_walks):seqs=[]for _ in tqdm(range(num_walks)):start_node = np.random.choice(g.nodes)w = walkOneTime(g,start_node, walk_length)seqs.append(w)return seqsdef deepwalk( g, dimensions = 10, walk_length = 80, num_walks = 10, min_count = 3 ):seqs = getDeepwalkSeqs(g, walk_length = walk_length, num_walks = num_walks)model = word2vec.Word2Vec(seqs, vector_size = dimensions, min_count = min_count)return modelif __name__ == '__main__':#快速随机生成一个有向图g = nx.fast_gnp_random_graph(n = 100, p = 0.5,directed = True) model = deepwalk( g, dimensions = 10, walk_length = 20, num_walks = 100, min_count = 3 )# 观察与节点2最相近的三个节点print(model.wv.most_similar('2',topn=3))# 可以把emd储存下来以便下游任务使用model.wv.save_word2vec_format('e.emd')# 可以把模型储存下来以便下游任务使用model.save('m.model')
- 先利用
networkx随机生成二项式有向图(如下图所示) walk_length是每条random walk链路的长度,共有num_walks条链路,通过随机游走得到的seqs送入到gensim.models.word2vec中训练w2v,保存训练得到的embedding和模型m.model。- 得到与节点2最接近的3个节点:
[('77', 0.8721016049385071), ('65', 0.8555149435997009), ('66', 0.8495140671730042)]。

2.4 小结

三、在同质性和结构性间权衡:Node2vec
2016 年,斯坦福大学大佬在 DeepWalk 的基础上提出了 Node2vec 模型。Node2vec 通过调整随机游走跳转概率的方法,让 Graph Embedding 的结果在网络的同质性(Homophily)和结构性(Structural Equivalence)中进行权衡,可以进一步把不同的 Embedding 输入推荐模型,让推荐系统学习到不同的网络结构特点。
3.1 同质性和结构性
网络的“同质性”指的是距离相近节点的 Embedding 应该尽量近似,如图 3 所示,节点 u 与其相连的节点 s1、s2、s3、s4的 Embedding 表达应该是接近的,这就是网络“同质性”的体现。在电商网站中,同质性的物品很可能是同品类、同属性,或者经常被一同购买的物品。
“结构性”指的是结构上相似的节点的 Embedding 应该尽量接近,比如图 3 中节点 u 和节点 s6都是各自局域网络的中心节点,它们在结构上相似,所以它们的 Embedding 表达也应该近似,这就是“结构性”的体现。在电商网站中,结构性相似的物品一般是各品类的爆款、最佳凑单商品等拥有类似趋势或者结构性属性的物品。


3.2 如何表达结构性和同质性
Graph Embedding 的结果究竟是怎么表达结构性和同质性的呢?
-
首先,为了使 Graph Embedding 的结果能够表达网络的“结构性”,在随机游走的过程中,我们需要让游走的过程更倾向于 BFS(Breadth First Search,宽度优先搜索),因为 BFS 会更多地在当前节点的邻域中进行游走遍历,相当于对当前节点周边的网络结构进行一次“微观扫描”。(当前节点是“局部中心节点”,还是“边缘节点”,亦或是“连接性节点”,其生成的序列包含的节点数量和顺序必然是不同的,从而让最终的 Embedding 抓取到更多结构性信息。)
-
而为了表达“同质性”,随机游走要更倾向于 DFS(Depth First Search,深度优先搜索)才行,因为 DFS 更有可能通过多次跳转,游走到远方的节点上。但无论怎样,DFS 的游走更大概率会在一个大的集团内部进行,这就使得一个集团或者社区内部节点的 Embedding 更为相似,从而更多地表达网络的“同质性”。
那在 Node2vec 算法中,究竟是怎样控制 BFS 和 DFS 的倾向性的呢?
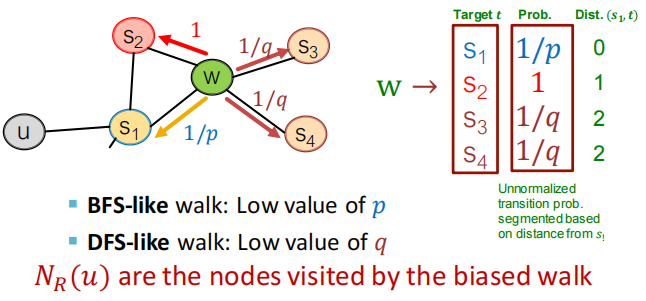
- 其实,它主要是通过节点间的跳转概率来控制跳转的倾向性。图 4 所示为 Node2vec 算法从节点 t 跳转到节点 v 后,再从节点 v 跳转到周围各点的跳转概率。这里,你要注意这几个节点的特点。比如,节点 t 是随机游走上一步访问的节点,节点 v 是当前访问的节点,节点 x1、x2、x3是与 v 相连的非 t 节点,但节点 x1还与节点 t 相连,这些不同的特点决定了随机游走时下一次跳转的概率。

这些概率还可以用具体的公式来表示,从当前节点 v 跳转到下一个节点 x 的概率πvx=αpq(t,x)⋅ωvx\pi_{v x}=\alpha_{p q}(t, x) \cdot \omega_{v x} πvx=αpq(t,x)⋅ωvx其中 Wvx 是边 vx 的原始权重,αpq(t,x)\alpha_{p q}(t, x)αpq(t,x) 是 Node2vec 定义的一个跳转权重。到底是倾向于 DFS 还是 BFS,主要就与这个跳转权重的定义有关了:
αpq(t,x)={1p如果 dtx=01如果 dtx=11q如果 dtx=2\alpha_{p q(t, x)=} \begin{cases}\frac{1}{p} & \text { 如果 } d_{t x}=0 \\ 1 & \text { 如果 } d_{t x}=1 \\ \frac{1}{q} & \text { 如果 } d_{t x}=2\end{cases} αpq(t,x)=⎩⎨⎧p11q1 如果 dtx=0 如果 dtx=1 如果 dtx=2
αpq(t,x)\alpha_{p q}(t, x)αpq(t,x)里的dtxd_{tx}dtx 是指节点 t 到节点 x 的距离,比如节点 x1其实是与节点 t 直接相连的,所以这个距离 dtxd_{tx}dtx就是 1,节点 t 到节点 t 自己的距离 dttd_{tt}dtt就是 0,而 x2、x3这些不与 t 相连的节点,dtxd_{tx}dtx就是 2。
此外,αpq(t,x)\alpha_{p q}(t, x)αpq(t,x) 中的参数 p 和 q 共同控制着随机游走的倾向性。参数 p 被称为返回参数(Return Parameter),p 越小,随机游走回节点 t 的可能性越大,Node2vec 就更注重表达网络的结构性。参数 q 被称为进出参数(In-out Parameter),q 越小,随机游走到远方节点的可能性越大,Node2vec 更注重表达网络的同质性。
反之,当前节点更可能在附近节点游走。可以自己尝试给 p 和 q 设置不同大小的值,算一算从 v 跳转到 t、x1、x2和 x3的跳转概率。这样应该就能理解刚才所说的随机游走倾向性的问题啦。
3.3 实验证实+代码例子
Node2vec 这种灵活表达同质性和结构性的特点也得到了实验的证实,可以通过调整 p 和 q 参数让它产生不同的 Embedding 结果。
- 图 5 上就是 Node2vec 更注重同质性的体现,从中可以看到,距离相近的节点颜色更为接近;
- 图 5 下则是更注重结构性的体现,其中结构特点相近的节点的颜色更为接近。

Node2vec 所体现的网络的同质性和结构性,在推荐系统中都是非常重要的特征表达。由于 Node2vec 的这种灵活性,以及发掘不同图特征的能力,可以把不同 Node2vec 生成的偏向“结构性”的 Embedding 结果,以及偏向“同质性”的 Embedding 结果共同输入后续深度学习网络,以保留物品的不同图特征信息。
【代码例子】通过Node2vec找到和节点2最接近的3个节点
import networkx as nx
from node2vec import Node2Vecgraph = nx.fast_gnp_random_graph(n=100, p=0.5)#快速随机生成一个无向图
node2vec = Node2Vec ( graph, dimensions=64, walk_length=30, num_walks=100, p=0.3,q=0.7,workers=4)#初始化模型
model = node2vec.fit()#训练模型
print(model.wv.most_similar('2',topn=3))# 观察与节点2最相近的三个节点
'''
[('43', 0.5867125988006592), ('41', 0.5798742175102234), ('33', 0.5246706008911133)]
'''
四、Embedding Entire Graphs
4.1 得到子图或整图的embedding
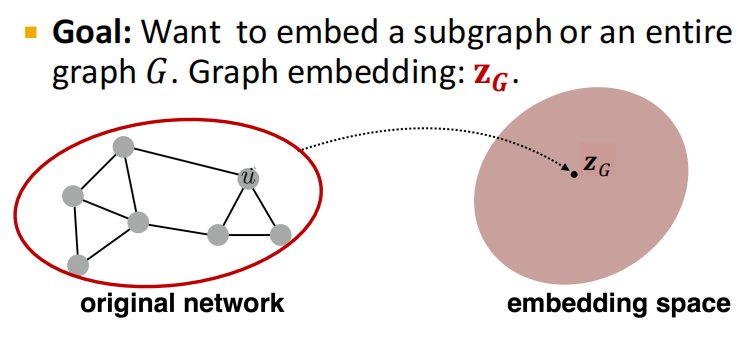
4.2 anonymous walks的应用
4.3 小结

附:思考题
机器学习中的“表示学习”是做什么的?为什么要做表示学习?
CS224W整门课程,都对哪些研究对象进行了嵌入编码的表示学习操作?
图嵌入有什么用?
图嵌入有哪几种技术方案?各有什么优劣?
如何理解图嵌入向量的“低维、连续、稠密”
如何衡量两个节点是否“相似”?
图嵌入中,Decoder为什么用两个向量的数量积?
如何理解图嵌入中的Shallow Encoder和Deep Encoder?有何区别?
随机游走序列包含了哪些信息?
图机器学习和自然语言处理存在怎样的对应关系?
简述DeepWalk算法原理
简述Node2Vec算法原理
除了DeepWalk和Node2Vec之外,还有哪些基于随机游走的图嵌入算法?
同济子豪兄论文精读视频中,DeepWalk和Node2Vec也留了不少思考题,去看看吧
你是否能想出更科学的随机游走策略?
基于随机游走的图嵌入方法,都可以被统一成什么样的数学形式?
重新思考:为什么要把图表示成矩阵的形式?
附:时间安排
| 任务 | 任务内容 | 截止时间 | 注意事项 |
|---|---|---|---|
| 2月11日开始 | |||
| task1 | 图机器学习导论 | 2月14日周二 | 完成 |
| task2 | 图的表示和特征工程 | 2月15、16日周四 | 完成 |
| task3 | NetworkX工具包实践 | 2月17、18日周六 | 完成 |
| task4 | 图嵌入表示 | 2月19、20日周一 | 完成 |
| task5 | deepwalk、Node2vec论文精读 | 2月21、22日周三 | |
| task6 | PageRank | 2月23、24日周五 | |
| task7 | 标签传播与节点分类 | 2月25、26日周日 | |
| task8 | 图神经网络基础 | 2月27、28日周二 | |
| task9 | 图神经网络的表示能力 | 3月1日周三 | |
| task10 | 图卷积神经网络GCN | 3月2日周四 | |
| task11 | 图神经网络GraphSAGE | 3月3日周五 | |
| task12 | 图神经网络GAT | 3月4日周六 |
Reference
[1] 传统图机器学习的特征工程-节点【斯坦福CS224W】
[2] cs224w(图机器学习)2021冬季课程学习笔记2: Traditional Methods for ML on Graphs
[3] NetworkX入门教程
[4] https://github.com/TommyZihao/zihao_course/tree/main/CS224W
[5] 斯坦福官方课程:https://web.stanford.edu/class/cs224w/
[6] 子豪兄github:https://github.com/TommyZihao/zihao_course
[7] 子豪:随机游走的艺术-图嵌入表示学习【斯坦福CS224W图机器学习】
[8] Graph Embedding-Node2vec总结
[9] nx.draw报错 ‘_AxesStack‘ object is not callable
[10] Embedding技术在推荐系统中的应用
[11] cs224w(图机器学习)2021冬季课程学习笔记3: Node Embeddings
[12] networkx官方文档:fast_gnp_random_graph
相关文章:

【CS224W】(task4)图嵌入表示学习
note node2vec: 计算随机游走概率从节点uuu开始模拟rrr条长度为lll的游走链路使用 Stochastic Gradient Descent 优化损失函数 Node2vec在节点分类方面表现更好;而其他方法在链路预测上效果更好,如random walk效率更高;graph emb…...

分享111个HTML医疗保健模板,总有一款适合您
分享111个HTML医疗保健模板,总有一款适合您 111个HTML医疗保健模板下载链接:https://pan.baidu.com/s/1YInaQDnUVsXYtMh1Ls-BHg?pwdxvfc 提取码:xvfc Python采集代码下载链接:采集代码.zip - 蓝奏云 import os import shuti…...

山东大学2022操作系统期末
接力:山东大学2021操作系统期末 2022—2023山东大学计算机操作系统期末考试回忆版 简答题(4 10 points) (1)用户态,核心态是什么 (2)这种区分对现代操作系统的意义 (3)printf(“…...

Hadoop高可用搭建(一)
目录 创建多台虚拟机 修改计算机名称 快速生效 修改网络信息 重启网络服务 关闭和禁用每台机的防火墙 同步时间 安装ntpdate 定时更新时间 启动定时任务 设置集群中每台机器的/etc/hosts 把hosts拷贝发送到每一台虚拟机 配置免密登陆 将本机的公钥拷贝到要免密登…...

算法 - 剑指Offer 重建二叉树
题目 输入某二叉树的前序遍历和中序遍历的结果,请构建该二叉树并返回其根节点。 假设输入的前序遍历和中序遍历的结果中都不含重复的数字。 解题思路 这题较为复杂, 首先审题,前序遍历规则:根左右, 中序遍历&#x…...

手写JavaScript常见5种设计模式
想分享的几种设计模式 目前模式:工厂模式,单例模式,适配器模式,装饰者模式,建造者模式 建造者模式 简介:建造者模式(builder pattern)比较简单,它属于创建型模式的一种…...
)
Python 异步: 当前和正在运行的任务(9)
我们可以反省在 asyncio 事件循环中运行的任务。这可以通过为当前运行的任务和所有正在运行的任务获取一个 asyncio.Task 对象来实现。 1. 如何获取当前任务 我们可以通过 asyncio.current_task() 函数获取当前任务。此函数将为当前正在运行的任务返回一个任务对象。 ... # …...
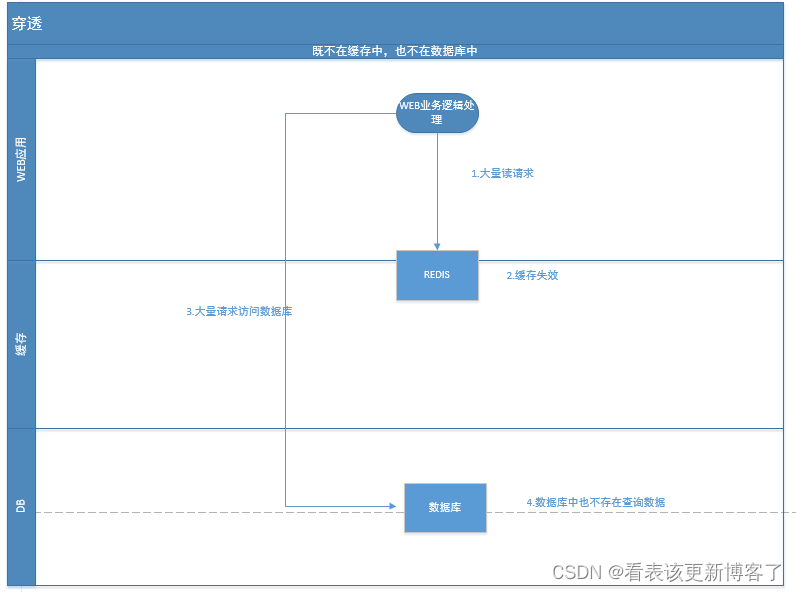
REDIS-雪崩、击穿、穿透
直接发车🚗 一.雪崩 1.触发原因 A.大量缓存数据在同一时间过期(失效) B.redis故障宕机 上述均导致全部请求去访问数据库,导致DB压力骤增,严重则导致数据库宕机/系统宕机 2.应对策略 不同触发原因,应对策略也不一致 应对A&a…...

什么人合适学习Python
发了几天的Python基础,也认识了一些朋友,忽然有人问起,说为啥学Python,或者说啥人学习Python,作为一个教龄8年从Python一线讲师到Python教学主管的我和大家分享一下个人的看法,还是提前说一下,个…...
greenDao的使用文档
介绍:greenDAO 是一款轻量级的 Android ORM 框架,将 Java 对象映射到 SQLite 数据库中,我们操作数据库的时候,不在需要编写复杂的 SQL语句, 在性能方面,greenDAO 针对 Android 进行了高度优化, …...

基于JAVA+SpringBoot+LayUI+Shiro的仓库管理系统
基于JAVASpringBootLayUIShiro的仓库管理系统 ✌全网粉丝20W,csdn特邀作者、博客专家、CSDN新星计划导师、java领域优质创作者,博客之星、掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域和毕业项目实战✌ 🍅文末获取项目下载方式🍅 一、项…...
金三银四面试必看,复盘字节测试开发面试:一次测试负责人岗位面试总结
最近面试了某企业的测试负责人岗位,历经四面,收获蛮多的。 这篇文章,我想聊聊这次面试过程中的一些经历,以及些许经验和教训。 岗位要求 岗位名称:测试负责人 岗位要求:1、扎实的技术以及丰富的技术项目…...
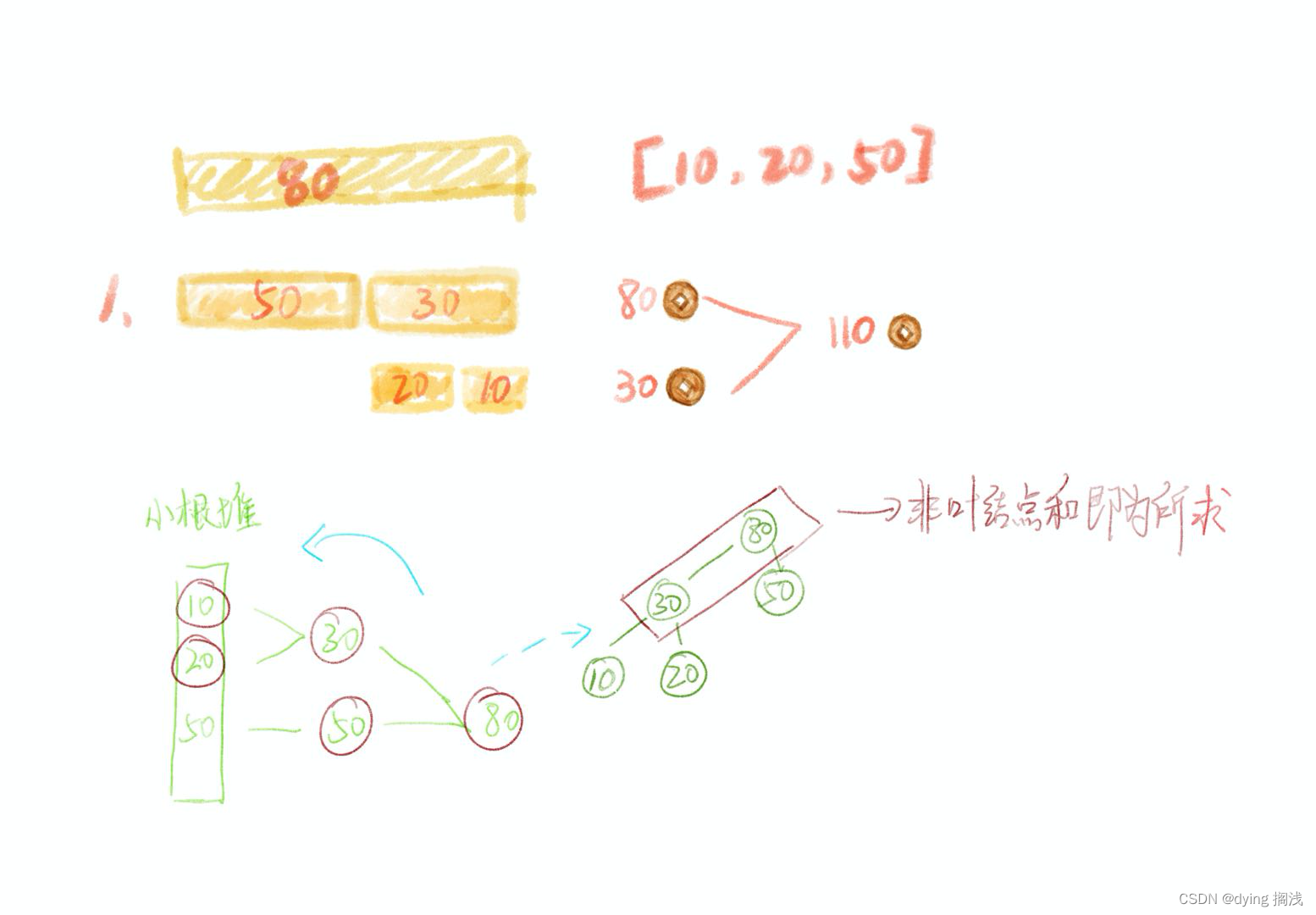
【算法自由之路】 贪心算法
贪心算法 局部最右得到全局最右难点在于如何证明局部最优可以得到全局最优堆 和 排序 是贪心算法最常用的实现算法 贪心算法作为最符合自然智慧的算法,思路是从小部分取最优从而获得最终的最优,但是难得是怎样获取部分最优才能得到全局最优。 有时候我…...

Scratch少儿编程案例-水果忍者-学生作业
专栏分享 点击跳转=>Unity3D特效百例点击跳转=>案例项目实战源码点击跳转=>游戏脚本-辅助自动化点击跳转=>Android控件全解手册点击跳转=>Scratch编程案例👉关于作者...

7.Docker Compose
Docker Compose 介绍 Docker Compose是Docker官方编排(Orchestration)项目之一,负责快速的部署分布式应用。其代码目前在https://github.com/docker/compose上开源。Compose 定位是 「定义和运行多个 Docker 容器的应用(Definin…...

GitHub访问问题与 Steam++下载及使用(适合小白)
前言 📜 “ 作者 久绊A ” 专注记录自己所整理的Java、web、sql等,IT技术干货、学习经验、面试资料、刷题记录,以及遇到的问题和解决方案,记录自己成长的点滴 目录 前言 一、Steam的介绍 1、大概介绍 2、详细介绍 二、Ste…...
Oracle对象——视图之简单视图与视图约束
文章目录什么是视图为什么会使用视图视图语法案例简单视图的创建更改数据基表,视图数据会变化么?更改视图数据,基表数据会变更么?带检查约束的视图结论创建只读视图(MySQL不支持)总结什么是视图 视图是一种…...

SAP模块常用增强总结
MM模块: 采购订单增强: BADI :ME_GUI_PO_CUST ME_PROCESS_PO_CUST 物料凭证增强: BADI:MB_DOCUMENT_BADI USER-EXIT:MBCF0002 实现功能1、当参照预留过帐时,检查填入数量是否小于预留数量 2…...

当make执行遇到 Arguments too long
1. 问题 Ubuntu20.04上make编译生成so的时候报错: make[1]:execvp:/bin/sh:Arguments too long对应makefile中的报错位置,仅仅是生成so的时候报错,伪代码如下 ${build_tool} -shared -fpic -o "$" ${OBJ_FILE} ${LDFLAGS}然而如…...

《手把手教你》系列基础篇(七十三)-java+ selenium自动化测试-框架设计基础-TestNG实现启动不同浏览器(详解教程)
1.简介 上一篇文章中,从TestNg的特点我们知道支持变量,那么我们这一篇就通过变量参数来启动不同的浏览器进行自动化测试。那么如何实现同时启动不同的浏览器对脚本进行测试,且听我娓娓道来。 2.项目实战 2.1创建一个TestNg class 1.首先按…...

LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器的上位机配置操作说明
LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器专为工业环境精心打造,完美适配AGV和无人叉车。同时,集成以太网与语音合成技术,为各类高级系统(如MES、调度系统、库位管理、立库等)提供高效便捷的语音交互体验。 L…...

shell脚本--常见案例
1、自动备份文件或目录 2、批量重命名文件 3、查找并删除指定名称的文件: 4、批量删除文件 5、查找并替换文件内容 6、批量创建文件 7、创建文件夹并移动文件 8、在文件夹中查找文件...

VTK如何让部分单位不可见
最近遇到一个需求,需要让一个vtkDataSet中的部分单元不可见,查阅了一些资料大概有以下几种方式 1.通过颜色映射表来进行,是最正规的做法 vtkNew<vtkLookupTable> lut; //值为0不显示,主要是最后一个参数,透明度…...

Unit 1 深度强化学习简介
Deep RL Course ——Unit 1 Introduction 从理论和实践层面深入学习深度强化学习。学会使用知名的深度强化学习库,例如 Stable Baselines3、RL Baselines3 Zoo、Sample Factory 和 CleanRL。在独特的环境中训练智能体,比如 SnowballFight、Huggy the Do…...

什么是Ansible Jinja2
理解 Ansible Jinja2 模板 Ansible 是一款功能强大的开源自动化工具,可让您无缝地管理和配置系统。Ansible 的一大亮点是它使用 Jinja2 模板,允许您根据变量数据动态生成文件、配置设置和脚本。本文将向您介绍 Ansible 中的 Jinja2 模板,并通…...

基于PHP的连锁酒店管理系统
有需要请加文章底部Q哦 可远程调试 基于PHP的连锁酒店管理系统 一 介绍 连锁酒店管理系统基于原生PHP开发,数据库mysql,前端bootstrap。系统角色分为用户和管理员。 技术栈 phpmysqlbootstrapphpstudyvscode 二 功能 用户 1 注册/登录/注销 2 个人中…...

Proxmox Mail Gateway安装指南:从零开始配置高效邮件过滤系统
💝💝💝欢迎莅临我的博客,很高兴能够在这里和您见面!希望您在这里可以感受到一份轻松愉快的氛围,不仅可以获得有趣的内容和知识,也可以畅所欲言、分享您的想法和见解。 推荐:「storms…...

从面试角度回答Android中ContentProvider启动原理
Android中ContentProvider原理的面试角度解析,分为已启动和未启动两种场景: 一、ContentProvider已启动的情况 1. 核心流程 触发条件:当其他组件(如Activity、Service)通过ContentR…...

Linux中《基础IO》详细介绍
目录 理解"文件"狭义理解广义理解文件操作的归类认知系统角度文件类别 回顾C文件接口打开文件写文件读文件稍作修改,实现简单cat命令 输出信息到显示器,你有哪些方法stdin & stdout & stderr打开文件的方式 系统⽂件I/O⼀种传递标志位…...

论文阅读:Matting by Generation
今天介绍一篇关于 matting 抠图的文章,抠图也算是计算机视觉里面非常经典的一个任务了。从早期的经典算法到如今的深度学习算法,已经有很多的工作和这个任务相关。这两年 diffusion 模型很火,大家又开始用 diffusion 模型做各种 CV 任务了&am…...
