【数据结构】选择排序(详细)
选择排序
- 1. 直接选择排序
- 2. 堆排序
- 2.1 堆
- 2.2 堆的实现(以大根堆为例)
- 2.3 堆排序
- 3. 堆排序(topK问题)
1. 直接选择排序
-
思想
以排升序为例。以a[i]为最大值(或最小值),从a[i+1]到a[n-1-i]比较选出最大值放在a[n-1-i](或最小值放在a[i])。简单讲就是将以每轮排序的第一个数作为最大值或者最小值,比较剩余的元素,得到最大值或者最小值,将最大值放在剩余数据的最后一位,最小值放在剩余数据的第一位。
升级版
以排升序为例。每轮排序中选出最大值和最小值,分别放在数据的左右两端。 -
例子(排升序)

-
代码实现
//选择排序(以排升序为例)
void Swap(int* p1, int* p2)
{int tmp = *p1;*p1 = *p2;*p2 = tmp;
}
void SelectSort(int* a, int n)
{int left = 0;int right = n - 1;while (left < right){int maxi = left, mini = left;for (int i = left + 1; i <= right; i++){if (a[i] > a[maxi]){maxi = i;}if (a[i] < a[mini]){mini = i;}}Swap(&a[maxi], &a[right]);//这里要考虑特殊情况:如果最小值mini==right,那么在交换maxi和right后,//最小值就发生改变,所以要最小值的下标要改变。if (mini == right){mini == maxi;}Swap(&a[mini], &a[left]);right--;left++;}
}
- 算法分析
时间复杂度
假设有n个元素,第一次排序要遍历n-2个元素,第二次排序要遍历n-4个元素,往后每次排序的元素个数都减2,总的遍历次数是等差数列的前n项和,所以时间复杂度是O(N^2)。
空间复杂度
空间复杂度是O(1)。
稳定性
是不稳定的排序。如上面的例子中的12,在选出最大值和最小值时,前后顺序发生改变。
注意
直接选择排序的最好情况和最坏情况的时间复杂度都是O(N^2)。
2. 堆排序
2.1 堆
-
概念
堆其实是一种树形结构,分为大根堆和小根堆。大根堆是树中所有父节点大于子节点,小根堆是树中所有父节点小于子节点。但父节点的左右孩子谁大谁小没有要求。 -
预备知识
(1)堆的逻辑结构是树,物理结构是数组(即在内存中以数组的形式存储)。
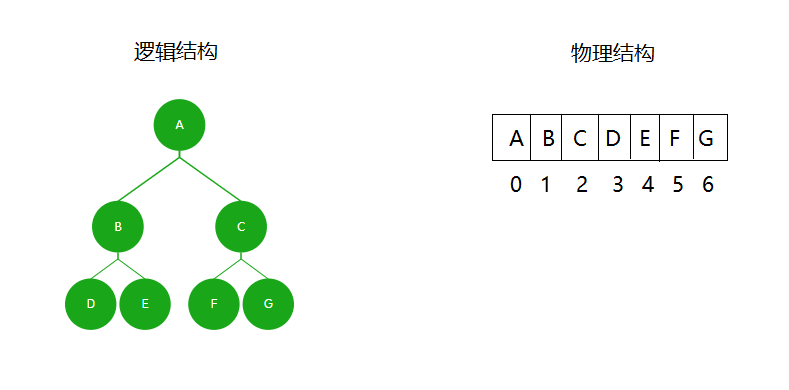
(2)父节点和子节点的关系
已知子节点下标,它的父节点下标parent = (child - 1)/2。
已知父节点下标,它的子节点下标leftchild = parent * 2 + 1,rightchild = parent * 2 + 2。
(3)种存储结构只适用于满二叉树和完全二叉树,否则会浪费很多空间。
2.2 堆的实现(以大根堆为例)
- 堆的定义
//堆的实现
typedef int HPDataType;
typedef struct Heap
{HPDataType* a;//用来申请空间int size;//记录当前堆的元素个数int capacity;//记录当前堆的最大容量
};
- 堆的初始化
//堆的初始化
void HeapInit(HP* ph)
{assert(ph);ph->a = (HPDataType*)malloc(sizeof(HPDataType)*10);//初始化容量设置为10if (ph->a == NULL){perror("malloc failed");return;}ph->capacity = 10;ph->size = 0;
}
- 入堆
//入堆
void HeapPush(HP* ph, HPDataType x)
{assert(ph);//首先要检查堆是否已满if (ph->size == ph->capacity){HPDataType* tmp = (HPDataType*)realloc(ph->a, sizeof(HPDataType) * ph->capacity * 2);if (tmp == NULL){perror("realloc failed");return;}ph->a = tmp;ph->capacity *= 2;//每次容量不够时扩容两倍}ph->a[ph->size++] = x;//因为要实现大根堆,如果入堆元素大于前面的元素,就要把它向上调整。AdjustUp(ph->a, ph->size - 1);//第一次参数是要调整的数据元素,第二个参数是入堆元素的下标。
}
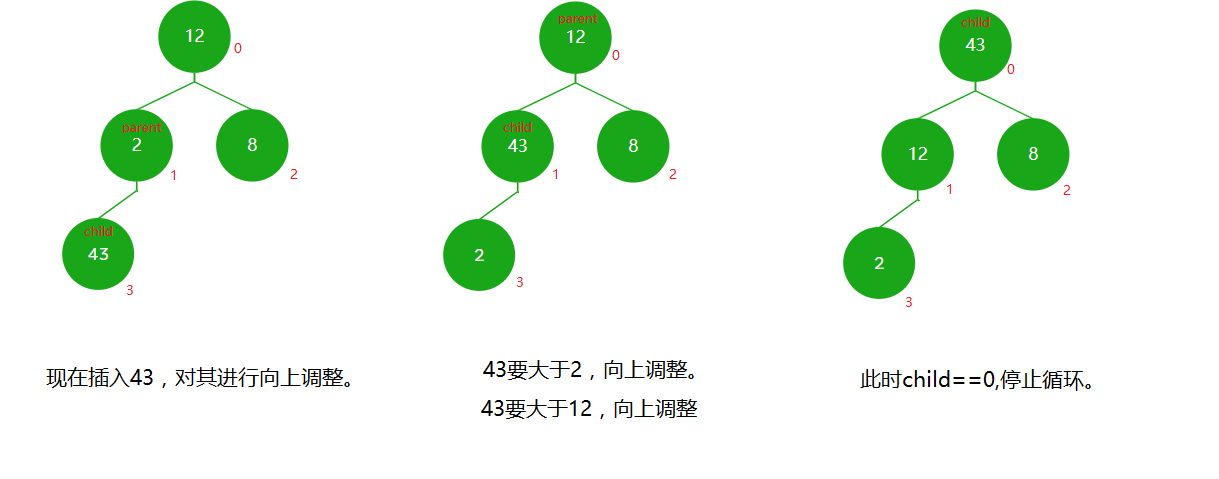
- 向上调整
//向上调整
void Swap(HPDataType* p1, HPDataType* p2)
{HPDataType tmp = *p1;*p1 = *p2;*p2 = tmp;
}
void AdjustUp(HPDataType* a, int child)
{//得到父节点的下标int parent = (child - 1) / 2;while (child > 0)//当子节点爬到下标为0的位置,就达到顶部了,此时可以停止循环{//比较父节点和子节点,谁大谁上去//让大的节点不断往上爬if (a[chil] > a[parent]){Swap(&a[child], &a[parent]);child = parent;parent = (child - 1) / 2;}else{break;}}
}
- 出堆
疑惑
(1)
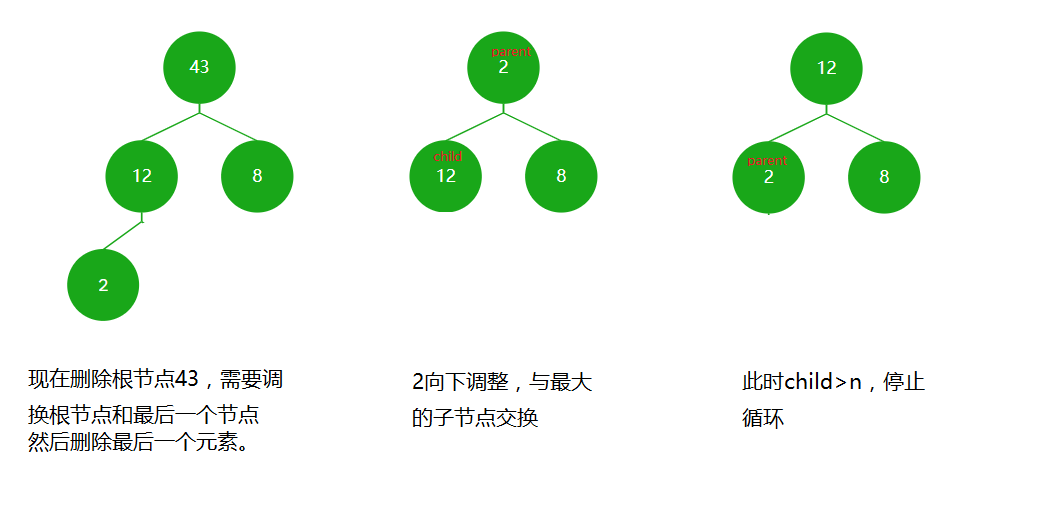
出堆其实就是弹出根节点。但我们要考虑弹出根节点后,后面的数据要如何处理?将数据往前移动?这样数据间的关系就全乱了,且所有数据往前移效率低(O(N^2))。
正确的做法是交换堆顶元素和最后一个元素,然后删除最后一个元素,然后将堆顶元素向下调整。
(2)
为什么要弹出根节点?弹出最后一个元素岂不是更简单?这就涉及到堆的应用。我们所写的是大根堆,根结点是这组数据的最大值,弹出根节点后,向下调整可以得到次大值,然后再弹出根节点。就这样,我们就得到这组数据的前n个最大值,比如得到年纪前50名,得到产品销量前100名。由此可见,弹出根结点是非常有用的。
代码实现
//堆空
bool HeapEmpty(HP* ph)
{assert(ph);return ph->size == 0;
}//出堆
void HeapPop(HP* ph)
{assert(ph);//首先判断堆是否为空assert(!HeapEmpty(ph));//交换堆顶元素和最后一个元素Swap(&ph->a[0], &ph->a[ph->size - 1]);//删除最后一个元素ph->size--;//向下调整AdjustDown(ph->a, ph->size, 0);//第一个参数是要调整的数据,第二个参数是数据的个数,第三个参数是要调整的位置
}
- 向下调整
//向下调整(条件:左右子树都是大根堆或者小根堆)
void AdjustDown(HPDataType* a, int n, int parent)
{int child = 2 * parent + 1;//先得到左孩子while (child < n)//当子节点的下标大于元素个数时停止循环{//如果右孩子存在且大于左孩子,那么就换成右孩子与父节点比较if (child + 1 < n && a[child + 1] > a[child]){++child;}if (a[child] > a[parent]){Swap(&a[child], &a[parent]);parent = child;child = 2 * parent + 1;}else{break;}}
}
- 堆顶
//堆顶
HP* HeapTop(HP* ph)
{assert(ph);//首先判断堆是否为空assert(!HeapEmpty(ph));return ph->a[ph->size - 1];
}
- 打印前K个元素
//打印前K个元素
void PrintK(HP* ph, int k)
{while (!HeapEmpty(ph) && k--){printf("%d ", HeapTop(ph));HeapPop(ph);}printf("\n");
}
- 销毁
//销毁
void HeapDestroy(HP* ph)
{assert(ph);free(ph->a);ph->a = 0;ph->capacity = 0;ph->size = 0;
}
2.3 堆排序
了解堆的基本操作后,就可以实现堆排序。
//法一
//堆排序(以排升序为例)
void HeapSort(int* a, int n)
{//建堆(大根堆或者小根堆)for (int i = 1; i < n; i++){AdjustUp(a, i);//从下标为1的元素不断插入,从而向上调整}//建大根堆后,就交换根结点和最后一个元素,每次交换都将最大值放在数据的最后面int end = n - 1;while (end > 0){Swap(&a[end], &a[0]);//交换最大值和最后一个元素AdjustDown(a, end, 0);//交换后最后一个元素不参与调整,所有元素个数只有end个//每次调整后都会将最大值放在根节点的位置--end;}
}
//法二
void HeapSort(int* a, int n)
{//从最后一个元素的父节点开始向下调整//目的是建成大根堆for (int i = (n - 1 - 1) / 2; i >= 0; i--){AdjustDown(a, n, i);}int end = n - 1;while (end > 0){Swap(&a[end], &a[0]);AdjustDown(a, end, 0);--end;}
}
时间复杂度
这两种方法唯一的不同就是法一前面是向上调整,法二前面是向下调整。要比较两种方法的时间复杂度就得比较向下调整和向上调整的时间复杂度。
-
向下调整的时间复杂度是O(N)

-
向上调整的时间复杂度是O(NlogN)
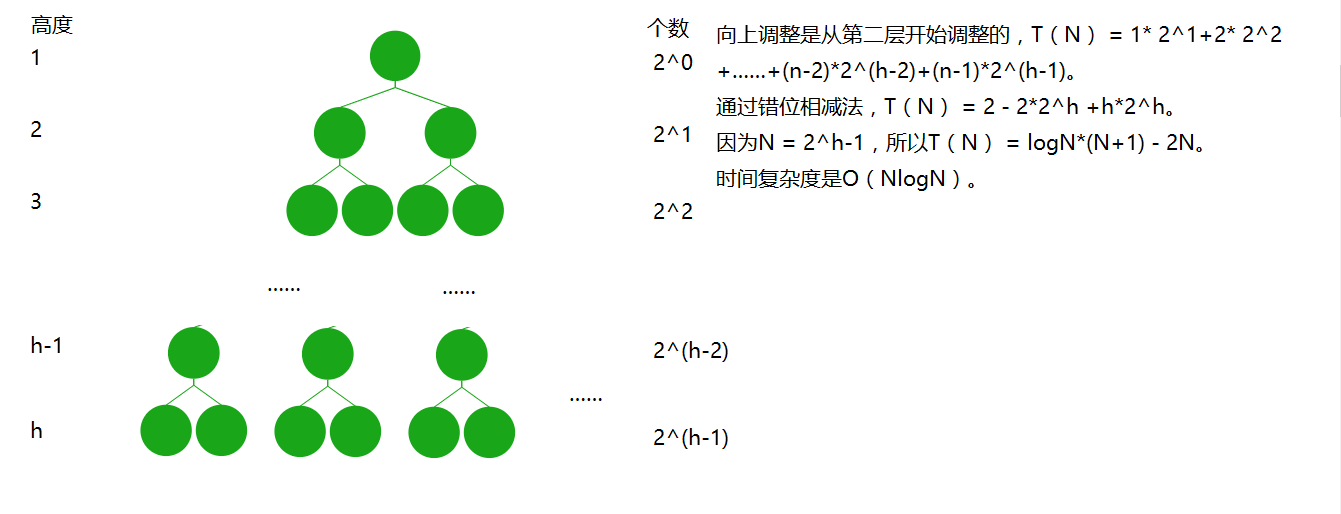
咋一看好像第二种方法时间复杂度更牛,但实际上这两种方法的时间复杂度都是O(NlogN)。我们讨论的只是向下调整和向上调整。
总的来说,堆排序的时间复杂度是O(NLogN)。两种方法都在这个量级,但第二种方法稍微高一点点。
3. 堆排序(topK问题)
找出N个数中最大的(或最小的)前K个数。
有两种方法:
法一:建N个大根堆,然后PopK次就可以。
法二:建有K个数的小根堆,遍历剩下的数据,如果数据比堆顶元素大,就替换它,然后向下调整,最后这个小根堆的数据就是最大的前K个。
这里主要用法二
void PrintTopK(const char* file, int k)
{//首先要建立小根堆int* topk = (int*)malloc(sizeof(int) * k);if (topk == NULL){perror("malloc failed");return;}//从文件中读取K个数据FILE* f = fopen(file, "r");if (f == NULL){perror("fopen failed");return;}for (int i = 0; i < k; i++){fscanf(f, "%d", &topk[i]);}//建小堆(之前写的向下调整是调整大根堆,只需修改其中一些>或者<即可)for (int i = (k - 1 - 1) / 2; i >= 0; i--){AdjustDown(topk, k, i);}//将剩下的n-k个元素依次与根节点比较,比它大就入堆且向下调整//这样将大的元素往下沉,小的元素不断换掉,最终只剩下最大的K个元素int val = 0;int ret = fscanf(f, "%d", &val);while (ret != EOF){if (val > topk[0]){topk[0] = val;AdjustDown(topk, k, 0);}ret = fscanf(f, "%d", &val);}for (int i = 0; i <k; i++){printf("%d ", topk[i]);}fclose(f);
}
void CreateData()
{int n = 1000;srand(time(0));const char* file = "TestData.txt";FILE* f = fopen("TestData.txt", "w");//以写的形式打开if (f == NULL){perror("fopen fail");return;}for (int i = 0; i < n; i++){int x = rand() % 1000;//获得0~999的数字fprintf(f, "%d ", x);}fclose(f);
}
相关文章:

【数据结构】选择排序(详细)
选择排序 1. 直接选择排序2. 堆排序2.1 堆2.2 堆的实现(以大根堆为例)2.3 堆排序 3. 堆排序(topK问题) 1. 直接选择排序 思想 以排升序为例。以a[i]为最大值(或最小值),从a[i1]到a[n-1-i]比较选…...

什么是企业内容管理?
为什么出现企业内容管理? 在数字经济的宏观背景下,企业建立了各种应用系统以满足企业各业务的管理需求,这些系统每天都在产生大量的数据和信息资源,但在企业实践中存在很多数据或资源无法被应用系统获取、处理和共享。 比如发票…...

机器学习:分类、回归、决策树
分类:具有明确的类别 如:去银行借钱,会有借或者不借的两种类别 回归:不具有明确的类别和数值 如:去银行借钱,预测银行会借给我多少钱,如:1~100000之间的一个数值 不纯度࿱…...

java常见的异常,下一篇写如何正确处理异常
当我们编写Java程序时,经常会遇到各种异常情况。异常是指在程序执行过程中发生的一些错误或意外情况,它会打断程序的正常执行流程,并且需要被适当地处理。在Java中,异常被分为两种类型:可检查异常(Checked …...

C#开发的OpenRA游戏之网络协议打包和解包
C#开发的OpenRA游戏之网络协议打包和解包 OpenRA游戏里,由于这是一个网络游戏,那么与服务器通讯就缺少不了, 既然要通讯,那么就需要协议,有协议就需要对数据进行打包和解包, 这个过程其实就是序列化与反序列化的过程。 游戏里很多命令都需要发送给服务器,以便服务器同…...

K8S通过Ansible安装集群
K8S通过Ansible安装集群 K8S集群安装可参考https://gitee.com/open-hand/kubeadm-ha.git、https://github.com/easzlab/kubeasz.git 安装高可用集群 git clone https://gitee.com/open-hand/kubeadm-ha.git && cd kubeadm-ha升级内核,非必需,默认不升级&…...

ChatGPT辩证观点:“人才不是一个企业的核心竞争力,对人才的管理能力才是一个企业的核心竞争力”
一、问: “人才不是一个企业的核心竞争力,对人才的管理能力才是一个企业的核心竞争力”这句话的理解和误解,这句话有哪个中心论点转移和变化 二、ChatGPT答: 这句话的理解和误解: 理解:这句话的意思是说…...

windows11 永久关闭windows defender的方法
1、按键盘上的windows按键,再点【设置】选项。 2、点击左侧菜单的【隐私和安全性】,再点击列表的【Windows安全中心】选项。 3、点击界面的【病毒和威胁保护】设置项。 4、病毒保护的全部关闭 5、别人的图(正常是都开着的) 6、终极…...

继承的基本知识
概念 假设基于A类,创建了B类,那么称A为B的父类,B为A的子类 子类会继承父类的成员变量及成员函数,但是不能继承构造、析构、运算符重载 假设又基于B创建了C,那么称B为C的直接基类,A为C的间接基类 继承按…...
【Frida-实战】EA游戏平台的文件监控(PsExec.exe提权)
▒ 目录 ▒ 🛫 问题描述环境 1️⃣ 代码编写开源代码搜索自己撸代码procexp确定句柄对应的文件名并过滤 2️⃣ PsExec.exe提权定位找不到EABackgroundService.exe的问题 PsExec.exe提权PsExec.exe原理 🛬 结论📖 参考资料 🛫 问题…...

可视化和回归分析星巴克咖啡在中国的定价建议
可视化和回归分析星巴克咖啡在中国的定价建议。星巴克的拿铁大杯Tall 在各国的价格。 Claude AI | 代码自动生成的数据可视化代码 选择Claude AI 而非 ChatGPT的理由是前者更懂中文!具体可以参见我前面的两篇文章对比两者的中英文翻译的表现及使用安装等难易程度…...

热门影片怎么买票比较便宜,低价买电影票的方法,纯攻略!
有时候真的有被自己蠢到!看电影看了这么多年,竟然不知道电影票价格才9.9元、19.9元就能买到。之前我看电影动不动就是几十上百块,感觉好亏啊。 其实,我也不敢相信的,通过这些平台,同时在节假日甚至春节档期…...

Python通过SWIG调用C++时出现的ImportError问题解析
摘要 win10系统,编译器为mingw,按照教程封装C的一个类并用python调用,一步步进行直到最后一步运行python代码时,在python代码中import example时报错ImportError: DLL load failed while importing _example: The specified modul…...

3ds Max云渲染有多快,3ds Max云渲染怎么用?
本地渲染效果图和动画3D项目是一个非常耗时的过程,当在场景中使用未优化的几何体或在最终渲染中使用大量多边形模型时,诸如此类的变量最终会增加渲染项目所需的时间和处理器能力。随着提供的渲染服务的云渲染平台出现,越来越多动画师、艺术家…...

Java之线程安全
目录 一.上节回顾 1.Thread类常见的属性 2.Thread类中的方法 二.多线程带来的风险 1.观察线程不安全的现象 三.造成线程不安全现象的原因 1.多个线程修改了同一个共享变量 2.线程是抢占式执行的 3.原子性 4.内存可见性 5.有序性 四.解决线程不安全问题 ---synchroni…...

我有一个方法判断你有没有编程天赋
我有一个方法判断你有没有编程天赋 一 前言 基于知识的诅咒的原理 做一个敲击者很难。问题在于敲击者已拥有的知识(歌曲题目)让 他们想象不到缺乏这种知识会是什么情形。当他们敲击的时候,他 们不能想象听众听到的是那些独立的敲击声而不是…...

python 生成chart 并以附件形式发送邮件
import requests import json import pandas as pd import numpy as np import matplotlib.pyplot as plt data np.random.randn(5, 3)#生成chart def generate_line_chart(data):df pd.DataFrame(np.abs(data),index[Mon, Tue, Wen, Thir, Fri],columns[A, B, C])df.plot()…...

leetcode-035-搜索插入位置
题目及测试 package pid035; /*35. 搜索插入位置 给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。请必须使用时间复杂度为 O(log n) 的算法。示例 1:输入: nums …...
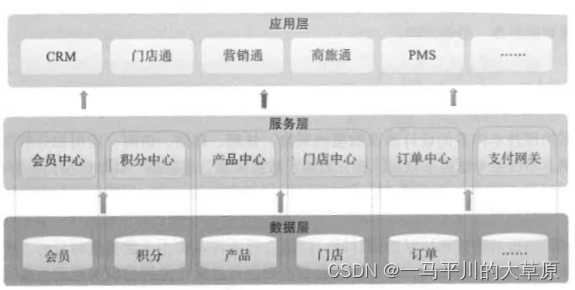
读书笔记--数据治理之法
继续延续上一篇文章,对数据治理之法进行学习。数据治理之法是战术层面的方法,是一套涵盖8项举措的数据治理实施方法论,包括梳理现状与确定目标、能力成熟度评估、治理路线图规划、保障体系建设、技术体系建设、治理策略执行与监控、绩效考核与…...

送了老弟一台 Linux 服务器,它又懵了!
大家好,我是鱼皮。 前两天我学编程的老弟小阿巴过生日,我问他想要什么礼物。 本来以为他会要什么游戏机、Q 币卡、鼠标键盘啥的,结果小阿巴说:我想要一台服务器。 鱼皮听了,不禁称赞道:真是个学编程的好苗…...

Vim 调用外部命令学习笔记
Vim 外部命令集成完全指南 文章目录 Vim 外部命令集成完全指南核心概念理解命令语法解析语法对比 常用外部命令详解文本排序与去重文本筛选与搜索高级 grep 搜索技巧文本替换与编辑字符处理高级文本处理编程语言处理其他实用命令 范围操作示例指定行范围处理复合命令示例 实用技…...

内存分配函数malloc kmalloc vmalloc
内存分配函数malloc kmalloc vmalloc malloc实现步骤: 1)请求大小调整:首先,malloc 需要调整用户请求的大小,以适应内部数据结构(例如,可能需要存储额外的元数据)。通常,这包括对齐调整,确保分配的内存地址满足特定硬件要求(如对齐到8字节或16字节边界)。 2)空闲…...

Cloudflare 从 Nginx 到 Pingora:性能、效率与安全的全面升级
在互联网的快速发展中,高性能、高效率和高安全性的网络服务成为了各大互联网基础设施提供商的核心追求。Cloudflare 作为全球领先的互联网安全和基础设施公司,近期做出了一个重大技术决策:弃用长期使用的 Nginx,转而采用其内部开发…...

Redis数据倾斜问题解决
Redis 数据倾斜问题解析与解决方案 什么是 Redis 数据倾斜 Redis 数据倾斜指的是在 Redis 集群中,部分节点存储的数据量或访问量远高于其他节点,导致这些节点负载过高,影响整体性能。 数据倾斜的主要表现 部分节点内存使用率远高于其他节…...

【分享】推荐一些办公小工具
1、PDF 在线转换 https://smallpdf.com/cn/pdf-tools 推荐理由:大部分的转换软件需要收费,要么功能不齐全,而开会员又用不了几次浪费钱,借用别人的又不安全。 这个网站它不需要登录或下载安装。而且提供的免费功能就能满足日常…...

使用Spring AI和MCP协议构建图片搜索服务
目录 使用Spring AI和MCP协议构建图片搜索服务 引言 技术栈概览 项目架构设计 架构图 服务端开发 1. 创建Spring Boot项目 2. 实现图片搜索工具 3. 配置传输模式 Stdio模式(本地调用) SSE模式(远程调用) 4. 注册工具提…...

Java毕业设计:WML信息查询与后端信息发布系统开发
JAVAWML信息查询与后端信息发布系统实现 一、系统概述 本系统基于Java和WML(无线标记语言)技术开发,实现了移动设备上的信息查询与后端信息发布功能。系统采用B/S架构,服务器端使用Java Servlet处理请求,数据库采用MySQL存储信息࿰…...

GruntJS-前端自动化任务运行器从入门到实战
Grunt 完全指南:从入门到实战 一、Grunt 是什么? Grunt是一个基于 Node.js 的前端自动化任务运行器,主要用于自动化执行项目开发中重复性高的任务,例如文件压缩、代码编译、语法检查、单元测试、文件合并等。通过配置简洁的任务…...

AirSim/Cosys-AirSim 游戏开发(四)外部固定位置监控相机
这个博客介绍了如何通过 settings.json 文件添加一个无人机外的 固定位置监控相机,因为在使用过程中发现 Airsim 对外部监控相机的描述模糊,而 Cosys-Airsim 在官方文档中没有提供外部监控相机设置,最后在源码示例中找到了,所以感…...

Windows安装Miniconda
一、下载 https://www.anaconda.com/download/success 二、安装 三、配置镜像源 Anaconda/Miniconda pip 配置清华镜像源_anaconda配置清华源-CSDN博客 四、常用操作命令 Anaconda/Miniconda 基本操作命令_miniconda创建环境命令-CSDN博客...
