非线性最小二乘
非线性最小二乘
目录
文章目录
- 非线性最小二乘
- 目录 @[toc]
- 1 非线性最小二乘估计
- 3 非线性最小二乘的实现
文章目录
- 非线性最小二乘
- 目录 @[toc]
- 1 非线性最小二乘估计
- 3 非线性最小二乘的实现
1 非线性最小二乘估计
在经典最小二乘法估计中,假定被解释变量的条件期望是关于参数的线性函数,例如
E ( y ∣ x ) = a + b x E(y|x) = a+bx E(y∣x)=a+bx
其中 a , b a,b a,b为待估参数, E ( y ∣ x ) E(y|x) E(y∣x)是关于参数 a , b a,b a,b的线性函数。但 E ( y ∣ x ) E(y|x) E(y∣x)是关于参数的非线性函数,则利用ols求出的正规方程组没有解析解。只能通过相关数值计算。考虑一个简单的非线性模型
Y i = β X 1 i + β 2 X 2 i + ε i Y_{i}=\beta X_{1 i}+\beta^{2} X_{2 i}+\varepsilon_{i} Yi=βX1i+β2X2i+εi
其中扰动项 ε i \varepsilon_i εi满足 E ( ε i ) = 0 , var ( ε i ) = σ 2 \mathrm{E}\left(\varepsilon_{i}\right)=0,\operatorname{var}\left(\varepsilon_{i}\right)=\sigma^{2} E(εi)=0,var(εi)=σ2,且为独立同分布。其残差平方和为
S ( β ) = ∑ i = 1 n ε i 2 = ∑ i = 1 n [ Y i − f ( X i , β ) ] 2 = ∑ i = 1 n [ Y i − β X 1 i − β 2 X 2 i ] 2 \begin{aligned} S(\beta) &=\sum_{i=1}^{n} \varepsilon_{i}^{2}=\sum_{i=1}^{n}\left[Y_{i}-f\left(X_{i}, \beta\right)\right]^{2} \\ &=\sum_{i=1}^{n}\left[Y_{i}-\beta X_{1 i}-\beta^{2} X_{2 i}\right]^{2} \end{aligned} S(β)=i=1∑nεi2=i=1∑n[Yi−f(Xi,β)]2=i=1∑n[Yi−βX1i−β2X2i]2
为了使回归线尽可能接近观测值,要求残差平方和最小。根据微积分的知识
d S d β = 2 ∑ i = 1 n [ Y i − f ( X i , β ) ] ( − d f ( X i , β ) d β ) = 2 ∑ i = 1 n [ Y i − β X 1 i − β 2 X 2 i ] [ − X 1 i − 2 β X 2 i ] = 0 \begin{aligned} \frac{\mathrm{d} S}{\mathrm{~d} \beta} &=2 \sum_{i=1}^{n}\left[Y_{i}-f\left(X_{i}, \beta\right)\right]\left(-\frac{\mathrm{d} f\left(X_{i}, \beta\right)}{\mathrm{d} \beta}\right) \\ &=2 \sum_{i=1}^{n}\left[Y_{i}-\beta X_{1 i}-\beta^{2} X_{2 i}\right]\left[-X_{1 i}-2 \beta X_{2 i}\right]=0 \end{aligned} dβdS=2i=1∑n[Yi−f(Xi,β)](−dβdf(Xi,β))=2i=1∑n[Yi−βX1i−β2X2i][−X1i−2βX2i]=0
整理得:
2 β 3 ∑ i = 1 n X 2 i 2 + 3 β 2 ∑ i = 1 n X 1 i X 2 i + β ( ∑ i = 1 n X 1 i 2 − 2 ∑ i = 1 n X 2 i Y i ) − ∑ i = 1 n X 1 i Y i = 0 2 \beta^{3} \sum_{i=1}^{n} X_{2 i}^{2}+3 \beta^{2} \sum_{i=1}^{n} X_{1 i} X_{2 i}+\beta\left(\sum_{i=1}^{n} X_{1 i}^{2}-2 \sum_{i=1}^{n} X_{2 i} Y_{i}\right)-\sum_{i=1}^{n} X_{1 i} Y_{i}=0 2β3i=1∑nX2i2+3β2i=1∑nX1iX2i+β(i=1∑nX1i2−2i=1∑nX2iYi)−i=1∑nX1iYi=0
这是关于参数 β \beta β的三次函数。尽管三次函数存在解析解(利用卡丹或盛金公式),其结果极为复杂。若上述三次方程存在实根 β i ( i = 1 , 2 , 3 ) \beta_i(i=1,2,3) βi(i=1,2,3)(最多三个),则将 β i \beta_i βi代入残差平方和,取 S ( β ) S(\beta) S(β)最小所对应的 β i \beta_i βi。上述例子中,被解释变量条件期望是关于参数的二次函数,如果将这种函数形式改为指数、对数或三角函数形式,则一般不存在解析解。
因此,数值分析自然成为解决上述问题的有力武器。考虑一般化的非线性回归问题,设总体回归模型满足
Y = f ( X , β ) + ε Y=f(X, \beta)+\varepsilon Y=f(X,β)+ε
对应的残差平方和为
S ( β ) = ∑ i = 1 n [ Y i − f ( X i , β ) ] 2 S(\beta)=\sum_{i=1}^{n}\left[Y_{i}-f\left(X_{i}, \beta\right)\right]^{2} S(β)=i=1∑n[Yi−f(Xi,β)]2
要使其最小化,需要满足一阶条件
d S d β = − 2 [ ∑ i = 1 n [ Y i − f ( X i , β ) ] ( − d f ( X i , β ) d β ) ] = 0 \frac{\mathrm{d} S}{\mathrm{~d} \beta}=-2\left[\sum_{i=1}^{n}\left[Y_{i}-f\left(X_{i}, \beta\right)\right]\left(-\frac{\mathrm{d} f\left(X_{i}, \boldsymbol{\beta}\right)}{\mathrm{d} \beta}\right)\right]=0 dβdS=−2[i=1∑n[Yi−f(Xi,β)](−dβdf(Xi,β))]=0
显然,上述问题不存在解析解,因此考虑对 f ( X i , β ) f(X_i, \beta) f(Xi,β)进行一阶泰勒展开。设参数向量 β \beta β的初始值为 β 1 \beta_1 β1,则可以在 β 1 \beta_1 β1附近找到函数 f ( X i , β ) f(X_i, \beta) f(Xi,β)使得
f ( X i , β ) ≈ f ( X i , β 1 ) + d f ( X i , β ) d β ∣ β = β 1 ( β − β 1 ) f\left(X_{i}, \beta\right) \approx f\left(X_{i}, \beta_{1}\right)+\frac{\mathrm{d} f\left(X_{i}, \beta\right)}{\mathrm{d} \beta} \mid_{\beta = \beta_{1}}\left(\beta-\beta_{1}\right) f(Xi,β)≈f(Xi,β1)+dβdf(Xi,β)∣β=β1(β−β1)
记 d f ( X i , β ) d β ∣ β 1 ≈ f ( X i , β ) − f ( X , β ) β − β 1 \left.\frac{\mathrm{d} f\left(X_{i}, \beta\right)}{\mathrm{d} \beta}\right|_{\beta_{1}} \approx \frac{f\left(X_{i}, \beta\right)-f(X, \beta)}{\beta-\beta_{1}} dβdf(Xi,β) β1≈β−β1f(Xi,β)−f(X,β),简记 X ~ i ( β 1 ) = d f ( X i , β ) d β ∣ β 1 \widetilde{X}_{i}\left(\beta_{1}\right)=\left.\frac{\mathrm{d} f\left(X_{i}, \beta\right)}{\mathrm{d} \beta}\right|_{\beta_{1}} X i(β1)=dβdf(Xi,β) β1,则
S ( β ) = ∑ i = 1 n [ Y i − f ( X i , β 1 ) − X ~ i ( β 1 ) ( β − β 1 ) ] 2 = ∑ i = 1 n [ Y ~ i ( β 1 ) − X i ( β 1 ) β ] 2 \begin{aligned} S(\beta) &=\sum_{i=1}^{n}\left[Y_{i}-f\left(X_{i}, \beta_{1}\right)-\widetilde{X}_{i}\left(\beta_{1}\right)\left(\beta-\beta_{1}\right)\right]^{2} \\ &=\sum_{i=1}^{n}\left[\widetilde{Y}_{i}\left(\beta_{1}\right)-X_{i}\left(\beta_{1}\right) \beta\right]^{2} \end{aligned} S(β)=i=1∑n[Yi−f(Xi,β1)−X i(β1)(β−β1)]2=i=1∑n[Y i(β1)−Xi(β1)β]2
其中
Y ~ i ( β 1 ) = Y i − f ( X i , β 1 ) + X ~ i ( β 1 ) β 1 \widetilde{Y}_{i}\left(\beta_{1}\right)=Y_{i}-f\left(X_{i}, \beta_{1}\right)+\widetilde{X}_{i}\left(\beta_{1}\right) \beta_{1} Y i(β1)=Yi−f(Xi,β1)+X i(β1)β1
给定初始值向量 β i \beta_i βi,则 Y ~ i ( β 1 ) \widetilde{Y}_{i}\left(\beta_{1}\right) Y i(β1)与 X ~ i ( β 1 ) \widetilde{X}_{i}\left(\beta_{1}\right) X i(β1)可计算,从而求出最小残差平方和。 S ( β ) S(\beta) S(β)对应的回归方程为
Y ~ i ( β 1 ) = X ~ i ( β ) β + ε i \widetilde{Y}_{i}\left(\beta_{1}\right)=\widetilde{X}_{i}(\beta) \beta+\varepsilon_{i} Y i(β1)=X i(β)β+εi
最小二乘估计量为
β 2 = [ X ~ ( β 1 ) ′ X ~ ( β 1 ) ] − 1 X ~ ( β 1 ) ′ Y ~ ( β 1 ) \beta_{2}=\left[\widetilde{X}\left(\beta_{1}\right)^{\prime} \widetilde{X}\left(\beta_{1}\right)\right]^{-1} \widetilde{X}\left(\beta_{1}\right)^{\prime} \widetilde{Y}\left(\beta_{1}\right) β2=[X (β1)′X (β1)]−1X (β1)′Y (β1)
其中
X ~ ( β 1 ) = [ X ~ 1 ( β 1 ) ⋮ X ~ n ( β 1 ) ] , Y ^ ( β 1 ) = [ Y ~ 1 ( β 1 ) ⋮ Y ~ n ( β 1 ) ] \widetilde{X}\left(\beta_{1}\right)=\left[\begin{array}{c} \widetilde{X}_{1}\left(\beta_{1}\right) \\ \vdots \\ \widetilde{X}_{n}\left(\beta_{1}\right) \end{array}\right], \quad \hat{Y}\left(\beta_{1}\right)=\left[\begin{array}{c} \widetilde{Y}_{1}\left(\beta_{1}\right) \\ \vdots \\ \widetilde{Y}_{n}\left(\beta_{1}\right) \end{array}\right] X (β1)= X 1(β1)⋮X n(β1) ,Y^(β1)= Y 1(β1)⋮Y n(β1)
此时我们求出 β 2 \beta_2 β2,再将 β 2 \beta_2 β2作为初始值依次迭代计算,得到关于向量参数 β i \beta_i βi的一个序列,当且仅当
∣ ∣ β ( k + 1 ) − β ( k ) ∣ ∣ < δ ||\beta^{(k+1)}-\beta^{(k)}||<\delta ∣∣β(k+1)−β(k)∣∣<δ
其中 δ > 0 \delta>0 δ>0为事先预定的绝对误差。不难得到,参数 β \beta β满足递推关系
β n + 1 = [ X ~ ( β n ) ′ X ~ ( β n ) ] − 1 X ~ ( β n ) ′ Y ~ ( β n ) = [ X ~ ( β n ) ′ X ~ ( β n ) ] − 1 X ~ ( β n ) ′ [ Y − f ( X ~ , β n ) + X ~ ( β n ) β n ] = β n + [ X ~ ( β n ) ′ X ~ ( β n ) ] − 1 X ~ ( β n ) ′ [ Y − f ( X , β n ) ] \begin{aligned} \boldsymbol{\beta}_{n+1} &=\left[\widetilde{X}\left(\boldsymbol{\beta}_{n}\right)^{\prime} \widetilde{X}\left(\boldsymbol{\beta}_{n}\right)\right]^{-1} \widetilde{X}\left(\boldsymbol{\beta}_{n}\right)^{\prime} \widetilde{Y}\left(\boldsymbol{\beta}_{n}\right) \\ &=\left[\widetilde{X}\left(\boldsymbol{\beta}_{n}\right)^{\prime} \widetilde{X}\left(\boldsymbol{\beta}_{n}\right)\right]^{-1} \widetilde{X}\left(\boldsymbol{\beta}_{n}\right)^{\prime}\left[\boldsymbol{Y}-f\left(\widetilde{X}, \boldsymbol{\beta}_{n}\right)+\widetilde{X}\left(\boldsymbol{\beta}_{n}\right) \boldsymbol{\beta}_{n}\right] \\ &=\boldsymbol{\beta}_{n}+\left[\widetilde{X}\left(\boldsymbol{\beta}_{n}\right)^{\prime} \widetilde{X}\left(\boldsymbol{\beta}_{n}\right)\right]^{-1} \widetilde{X}\left(\boldsymbol{\beta}_{n}\right)^{\prime}\left[Y-f\left(X, \boldsymbol{\beta}_{n}\right)\right] \end{aligned} βn+1=[X (βn)′X (βn)]−1X (βn)′Y (βn)=[X (βn)′X (βn)]−1X (βn)′[Y−f(X ,βn)+X (βn)βn]=βn+[X (βn)′X (βn)]−1X (βn)′[Y−f(X,βn)]
通过证明,随着样本容量 n → ∞ n\to\infty n→∞,参数 β \beta β估计量服从渐进正态分布,即
β ~ ∼ N ( β , σ ^ 2 [ X ~ ( β ) ′ X ~ ( β ) ] − 1 ) , σ ^ 2 = S ( β ~ ) n − 1 \widetilde{\beta} \sim N\left(\beta, \hat{\sigma}^{2}\left[\widetilde{X}(\beta)^{\prime} \widetilde{X}(\beta)\right]^{-1}\right), \hat{\sigma}^{2}=\frac{S(\widetilde{\beta})}{n-1} β ∼N(β,σ^2[X (β)′X (β)]−1),σ^2=n−1S(β )
3 非线性最小二乘的实现
在R语言中,可以适用nls函数实现非线性最小二乘法。以C-D函数为例,
设一国产出取决于资本、劳动与全要素的投入,即
Y = A K α L β μ Y = AK^{\alpha}L^{\beta}\mu Y=AKαLβμ
下面通过R代码运行实现对参数 α , β \alpha,\beta α,β的估计
t = 1:12 #时间设定
Y=c(26.74, 34.81, 44.72, 57.46, 73.84, 88.45, 105.82,126.16, 150.9, 181.6, 204.3, 222.8) #产出序列
K=c(23.66,30.55,38.12,46.77,56.45,67.15,78.92,91.67,105.5, 121.3, 128.6, 132.5) #资本序列
L=c(26, 28, 32, 36, 41, 45, 48, 52, 56, 60, 66, 70) #劳动投入序列
Cdnls <- nls(Y~A*K^a*L^b,start = list(A = 0.1,a = 0.5,b = 0.5)) #非线性最小二乘,start为参数初始值向量
summary(Cdnls)
#-------------------运行结果---------------------------
#Formula: Y ~ A * K^a * L^b
Parameters:Estimate Std. Error t value Pr(>|t|)
A 0.1129 0.0159 7.12 5.6e-05 ***
a 0.6568 0.0652 10.07 3.4e-06 ***
b 1.0298 0.1044 9.86 4.0e-06 ***
---
Signif. codes:
0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1Residual standard error: 1.7 on 9 degrees of freedomNumber of iterations to convergence: 9
Achieved convergence tolerance: 7.55e-06
结果显示,参数 α = 0.6568 \alpha = 0.6568 α=0.6568, β = 1.0298 \beta = 1.0298 β=1.0298。对比直接取对数的OLS,即估计
l n Y = l n A + α l n K + β l n L + e lnY = lnA+\alpha lnK+\beta lnL+e lnY=lnA+αlnK+βlnL+e
CDlm <- lm(log(Y)~log(K)+log(L)) #对数形式
summary(CDlm)
#--------------------运行结果--------------
Call:
lm(formula = log(Y) ~ log(K) + log(L))Residuals:Min 1Q Median 3Q Max
-0.02714 -0.00595 -0.00118 0.00764 0.02557 Coefficients:Estimate Std. Error t value Pr(>|t|)
(Intercept) -2.0737 0.2355 -8.80 1.0e-05 ***
log(K) 0.6258 0.0916 6.83 7.6e-05 ***
log(L) 1.0379 0.1621 6.40 0.00012 ***
---
Signif. codes:
0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1Residual standard error: 0.0173 on 9 degrees of freedom
Multiple R-squared: 1, Adjusted R-squared: 0.999
F-statistic: 9.16e+03 on 2 and 9 DF, p-value: 1.29e-15
结果显示,参数 α = 0.6268 \alpha = 0.6268 α=0.6268, β = 1.0379 \beta = 1.0379 β=1.0379。因此,CD函数对数化的结果回归与非线性最小二乘回归的参数基本一致。但一些不能对数化的方程,非线性最小二乘的作用更为明显。考虑真实模型
y = 2 s i n ( x ) + 4 c o s ( x ) y = 2sin(x)+4cos(x) y=2sin(x)+4cos(x)
接下来我们进行仿真模拟
set.seed(123) #随机种子
x <- seq(1,100,by = 0.1) #1-100,步长为0.1
e <- rnorm(length(x),0,1) #长度为序列x的长度,服从标准正态分布的误差
y <- 2*sin(x)+4*cos(x)+e #实际观测的被解释变量
plot(x,y,type = "o") #打印散点图nls1 <- nls(y~a*sin(x)+b*cos(x),start = list(a = 0,b =0)) #非线性最小二乘,初始值设定为0,0
nls1
#-------------运行结果------------------
Nonlinear regression modelmodel: y ~ a * sin(x) + b * cos(x)data: parent.frame()a b
1.92 4.03 residual sum-of-squares: 974Number of iterations to convergence: 1
Achieved convergence tolerance: 6.73e-10
结果显示估计量 a = 1.92 a = 1.92 a=1.92, b = 4.03 b = 4.03 b=4.03,与总体参数 a = 2 , b = 4 a = 2,b = 4 a=2,b=4即为接近
参考文献
王斌会(2015).计量经济学建模及R语言应用[M].北京大学出版社
相关文章:

非线性最小二乘
非线性最小二乘 目录 文章目录 非线性最小二乘目录 [toc]1 非线性最小二乘估计3 非线性最小二乘的实现 1 非线性最小二乘估计 在经典最小二乘法估计中,假定被解释变量的条件期望是关于参数的线性函数,例如 E ( y ∣ x ) a b x E(y|x) abx E(y∣x)a…...

23.5.7总结(学习通项目思路)
项目: 1.登录修改:删除数据库中的状态,通过使用 ConcurrentHashMap来作为是否在线的判断,通过设定一个退出的按钮,发消息给服务端主动移除对应的值。 2.注册:增加了手机号的填写,正则判断&…...

如何生成api接口获取宝贝商品详情,商品详情接口,产品详情
API (Application Programming Interface)是指应用程序接口,它是一种通过编写一组统一的规则,开发一个软件来与其他应用程序进行通讯的技术。API可以方便应用程序之间的交流和数据共享,以及增强应用程序的功能。 在现代应用程序中࿰…...
微服务---Redis实用篇-黑马头条项目-登录功能(短信验证缓存,用户信息缓存)
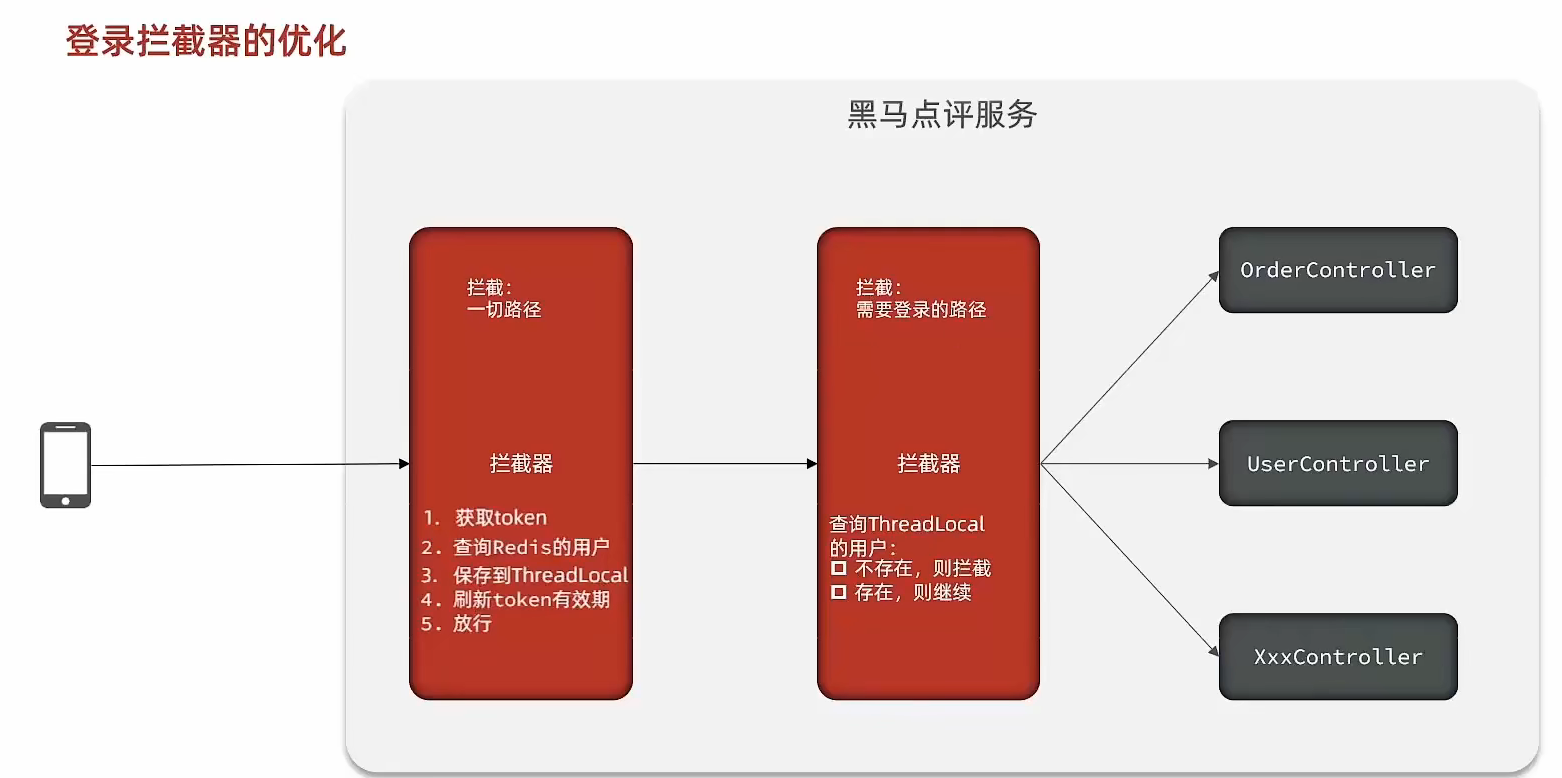
黑马头条项目-登录功能(短信验证缓存,用户信息缓存) 1、短信登录 1.1、导入黑马点评项目 1.1.1 、导入SQL 1.1.2、有关当前模型 手机或者app端发起请求,请求我们的nginx服务器,nginx基于七层模型走的事HTTP协议,可以实现基于Lua直接绕开t…...

美国纽扣电池的包装电池盒必须附带警告标签16 CFR 第 1700.20
美国纽扣电池及硬币电池的包装、电池盒必须附带警告标签16 CFR 第 1700.20 美国要求在纽扣电池或硬币电池的包装上、电池盒上以及包含纽扣电池或硬币电池的消费品附带说明和手册上贴上警告标签。 商品法规、标准和要求纽扣电池和硬币电池以下所有项: 16 CFR 第 17…...
AcWing——方格迷宫(有点不一样的迷宫问题)
4943. 方格迷宫 - AcWing题库 1、题目 给定一个 n 行 m 列的方格矩阵。 行从上到下依次编号为 1∼n,列从左到右依次编号为 1∼m。 第 i 行第 j 列的方格表示为 (i,j)。 矩阵中的方格要么是空地(用 . 表示),要么是陷阱…...

《常规脉搏传输时间作为人体血压变化标志》阅读笔记
目录 一、论文摘要 二、论文十问 Q1: 论文试图解决什么问题? Q2: 这是否是一个新的问题? Q3: 这篇文章要验证一个什么科学假设? Q4: 有哪些相关研究?如何归类?谁是这一课题在领域内值得关注的研究员? …...

java学习之异常三
目录 一、throws 一、基本说明 二、使用细节 二、自定义异常 一、 基本概念 编辑二、自定义异常的步骤 三、实例 四、练习 三、throw和throws的区别 四、本章作业 第一道 第二题 第三题 第四题 一、throws 一、基本说明 package com.hspedu.throws_;import java.i…...

生产者向 Kafka 发送消息的执行流程
(1)生产者要往 Kafka 发送消息时,需要创建 ProducerRecoder,代码如下: ProducerRecord<String,String> record new ProducerRecoder<>("CostomerCountry","Precision Products","Fr…...

Linux命令·netstat
netstat命令用于显示与IP、TCP、UDP和ICMP协议相关的统计数据,一般用于检验本机各端口的网络连接情况。netstat是在内核中访问网络及相关信息的程序,它能提供TCP连接,TCP和UDP监听,进程内存管理的相关报告。 如果你的计算机有时候…...

《心安即是归处》读书笔记
目录 作者简介 经典摘录 一个人活在世界上,必须处理好三个关系 什么叫人生呢? 谈一下人性的问题 了解人生的意义与价值 人生之美 评断一本书的好与坏有什么标准呢? 知足知不足 作者简介 季羡林,随便查询一下作者简介&…...
C++:使用红黑树封装map和set
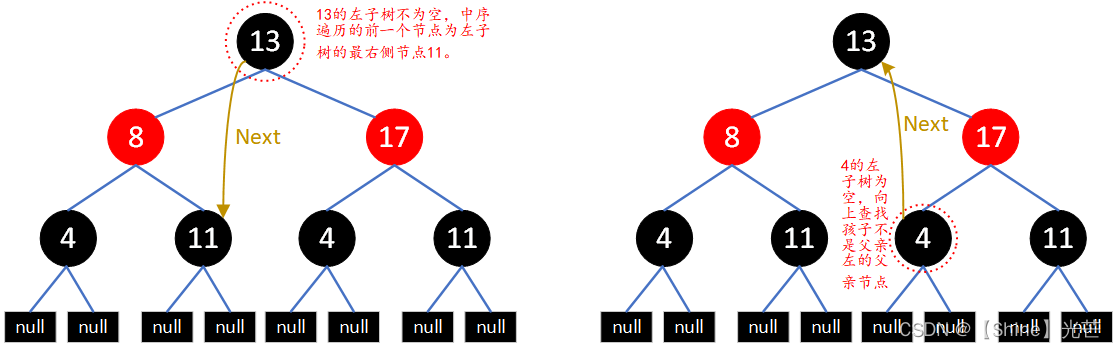
目录 一. 如何使用一颗红黑树同时实现map和set 二. 红黑树的节点插入操作 三. 红黑树迭代器的实现 3.1 begin()和end() 3.2 operator和operator-- 3.3 红黑树迭代器实现完整版代码 四. map和set的封装 附录:用红黑树封装map和set完整版代码 1. RBTree.h文件…...

Go 命令
目录 文章目录 go buildgo cleango fmtgo getgo installgo testgo toolgo generategodoc其它命令 go build 这个命令主要用于编译代码。在包的编译过程中,若有必要,会同时编译与之相关联的包。 如果是普通包,就像我们在1.2节中编写的mymath包…...

LEO、HW、LSO、LW 分别代表什么?
LEO :是 LogEndOffset 的简称,代表当前日志文件中下一条。HW:水位或水印一词,也可称为高水位 (high watermark) ,通常被用在流式处理领域 (flink、spark) ,以表征元素…...
(二分答案))
问题 B: 跳石头(C++)(二分答案)
目录 1.题目描述 2.AC 1.题目描述 问题 B: 跳石头 时间限制: 1.000 Sec 内存限制: 128 MB提交 状态 题目描述 一年一度的“跳石头”比赛又要开始了! 这项比赛将在一条笔直的河道中进行,河道中分布着一些巨大岩石。组委会已经选择好了两块岩石作为比赛起点和终点。在起点…...

bugku——变量1
拿到题目后是一串PHP代码,给到提示是flag在变量中,接下来进行代码审计 error_reporting(0):关闭错误报告 include “flag1.php”:包含flag1.php文件 highlight_file(_file_):页面进行语法高亮显示 isset($_GET[‘args’])…...

网络数据包丢失监控
什么是网络数据包 数据包或网络数据包是通过网络传输的小数据单元。顾名思义,这些是小的、离散的数据单元。单独来看,这些单位不一定有多大意义。它们只是正在传输的整体消息的一部分,这些消息已被组装成多个层。但是,当组合在一…...

Linux服务器安装部署MongoDB数据库 - 无公网IP远程连接
目录 前言 1. 配置Mongodb源 2. 安装MongoDB 3. 局域网连接测试 4. 安装cpolar内网穿透 5. 配置公网访问地址 6. 公网远程连接 7. 固定连接公网地址 8. 使用固定地址连接 转载自Cpolar Lisa文章:Linux服务器安装部署MongoDB数据库 - 无公网IP远程连接「内网…...

CSS面试题:30道含答案和代码示例的练习题
什么是 CSS?它的作用是什么? CSS(层叠样式表)是一种用于描述网页样式的语言。它的作用是控制网页的布局、字体、颜色、背景等方面的样式。如何在 HTML 页面中引入 CSS? 可以使用 标签将 CSS 文件引入到 HTML 页面中。例…...
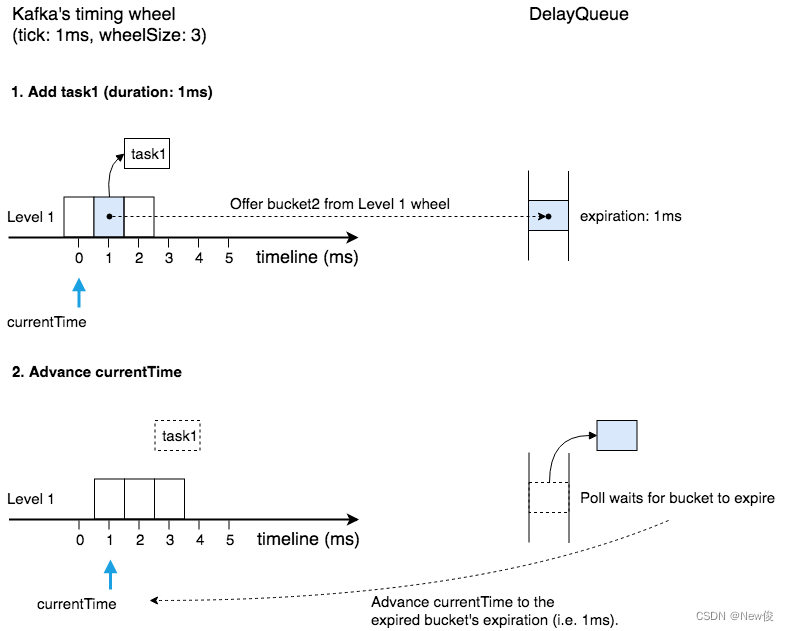
时间轮的golang实践浅析
引言 下列代码模仿一段RPC请求的执行过程,执行后会有哪些问题: RPC代码示例答案:因为超时控制后未阻断后续请求,导致并发读写产生Panic思考:客户端发起 HTTP 请求后,如果在指定时间内没有收到服务器的响应…...

铭豹扩展坞 USB转网口 突然无法识别解决方法
当 USB 转网口扩展坞在一台笔记本上无法识别,但在其他电脑上正常工作时,问题通常出在笔记本自身或其与扩展坞的兼容性上。以下是系统化的定位思路和排查步骤,帮助你快速找到故障原因: 背景: 一个M-pard(铭豹)扩展坞的网卡突然无法识别了,扩展出来的三个USB接口正常。…...

深度学习在微纳光子学中的应用
深度学习在微纳光子学中的主要应用方向 深度学习与微纳光子学的结合主要集中在以下几个方向: 逆向设计 通过神经网络快速预测微纳结构的光学响应,替代传统耗时的数值模拟方法。例如设计超表面、光子晶体等结构。 特征提取与优化 从复杂的光学数据中自…...

国防科技大学计算机基础课程笔记02信息编码
1.机内码和国标码 国标码就是我们非常熟悉的这个GB2312,但是因为都是16进制,因此这个了16进制的数据既可以翻译成为这个机器码,也可以翻译成为这个国标码,所以这个时候很容易会出现这个歧义的情况; 因此,我们的这个国…...

JavaSec-RCE
简介 RCE(Remote Code Execution),可以分为:命令注入(Command Injection)、代码注入(Code Injection) 代码注入 1.漏洞场景:Groovy代码注入 Groovy是一种基于JVM的动态语言,语法简洁,支持闭包、动态类型和Java互操作性,…...

基于ASP.NET+ SQL Server实现(Web)医院信息管理系统
医院信息管理系统 1. 课程设计内容 在 visual studio 2017 平台上,开发一个“医院信息管理系统”Web 程序。 2. 课程设计目的 综合运用 c#.net 知识,在 vs 2017 平台上,进行 ASP.NET 应用程序和简易网站的开发;初步熟悉开发一…...

uni-app学习笔记二十二---使用vite.config.js全局导入常用依赖
在前面的练习中,每个页面需要使用ref,onShow等生命周期钩子函数时都需要像下面这样导入 import {onMounted, ref} from "vue" 如果不想每个页面都导入,需要使用node.js命令npm安装unplugin-auto-import npm install unplugin-au…...

376. Wiggle Subsequence
376. Wiggle Subsequence 代码 class Solution { public:int wiggleMaxLength(vector<int>& nums) {int n nums.size();int res 1;int prediff 0;int curdiff 0;for(int i 0;i < n-1;i){curdiff nums[i1] - nums[i];if( (prediff > 0 && curdif…...

多模态商品数据接口:融合图像、语音与文字的下一代商品详情体验
一、多模态商品数据接口的技术架构 (一)多模态数据融合引擎 跨模态语义对齐 通过Transformer架构实现图像、语音、文字的语义关联。例如,当用户上传一张“蓝色连衣裙”的图片时,接口可自动提取图像中的颜色(RGB值&…...

【配置 YOLOX 用于按目录分类的图片数据集】
现在的图标点选越来越多,如何一步解决,采用 YOLOX 目标检测模式则可以轻松解决 要在 YOLOX 中使用按目录分类的图片数据集(每个目录代表一个类别,目录下是该类别的所有图片),你需要进行以下配置步骤&#x…...

华为云Flexus+DeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建
华为云FlexusDeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建 前言 如今大模型其性能出色,华为云 ModelArts Studio_MaaS大模型即服务平台华为云内置了大模型,能助力我们轻松驾驭 DeepSeek-V3/R1,本文中将分享如何…...
